10-Introduction

Algorithm

$$\mathrm{Algorithm}+\mathrm{Data}\mathrm{Structure}=\mathrm{Program}$$ $$(\mathrm{Algo}+\mathrm{DS})\times \mathrm{Efficiency}=\mathrm{Computation}$$

时间复杂度

T-notation

$$T_A(P)=算法A求解问题P的计算成本$$ $$T_A(n)=算法A求解问题规模为n的计算成本$$

A 在上下文确定时，可以省略。

$$T(n)=max\{T(P)||P|=n\}$$

只关注成本最高者。

big-O-notation

渐进分析 (Asymptotic analysis)：只关心问题规模足够大（$n\to \infty$）后，计算成本的增长趋势。

大 O 记号：

$$T(n)=O(f(n))$$

当且仅当，$\forall n\gg 2,\exists c>0,使得T(n)<c\cdot f(n)$

推论：

1. $n\gg 2时，O(f(n))=O(c\cdot f(n))$;
2. $O(n^a+n^b)=O(n^a),a\ge b>0$;
3. ${\lim }_{n\to \infty }\frac{T(n)}{f(n)}$ 不一定存在;

举例：

$$\begin{array}{rl}& \sqrt{5n[3n(n+2)+4]+6}\\ & <\sqrt{5n[6n^2+4]+6}\\ & <\sqrt{35n^{3+6}}\\ & <6\cdot n^{1.5}\\ & =O(n^{1.5})\end{array}$$

$O(f(n))$ 是 $T(n)$ 的上界渐进，作为 $n$ 充分大时对 $T(n)$ 的悲观估计。

Ω-notation

当且仅当 $\forall n\gg 2,\exists c>0,使得T(n)>c\cdot f(n)$，记为：

$$T(n)=\Omega (f(n))$$

$\Omega (f(n))$ 是 $T(n)$ 的下界渐进，作为 $n$ 充分大时对 $T(n)$ 的乐观估计。

Θ-notation

当且仅当 $\forall n\gg 2,\exists c_1>c_2>0,使得c_1\cdot f(n)>T(n)>c_2\cdot f(n)$，记为：

$$T(n)=\Theta (f(n))$$

$\Theta (f(n))$ 是 $T(n)$ 的确界，作为 $n$ 充分大时对 $T(n)$ 渐近紧致的估计。

大 O 记号的多项式

$O(1)$: constant

$O(\log n)$: ploy-log

• 底数无所谓；
• 常系数无所谓；
• 常数次幂无所谓：$\forall c>0,\log n^c=c\cdot \log n=\Theta (\log n)$;
  • 举例：

$$\begin{array}{c}\begin{array}{rl}123\cdot {\log }^{321}n& +{\log }^{205}(7\cdot n^2-15n+31)\\ & <123\cdot {\log }^{321}n+{\log }^{205}(8n^2)\\ & <123\cdot {\log }^{321}n+2\cdot {\log }^{205}(3n)\\ & =\Theta ({\log }^{321}n)\end{array}\end{array}$$

• 复杂度接近常数：$\forall c>0,\log n=O(n^c)$;
  • $\underset{n\to \infty }{\lim }\frac{\ln (n)}{n^c}=0$;

$O(n^c)$: polynomial

$a_k\cdot n^k+a_{k-1}\cdot n^{k-1}+\cdots +a_2\cdot n^2+a_1\cdot n^1+a_0=O(n^k),a_k>0$

$O(2^n)$: exponential

无穷级数表示指数： $e^n=1+n+\frac{n^2}{2!}+\frac{n^3}{3!}+\dots$ 因而 $\forall c>1,n^c<e^n=O(2^n)$

$O(n^c)$ 到 $O(2^n)$ 是有效算法到无效算法的分水岭。

NPC 问题：Non-Polynomial complete 典型如 2-Subset 问题，其有定理 $|2^S|=2^{|S|}=2^n$

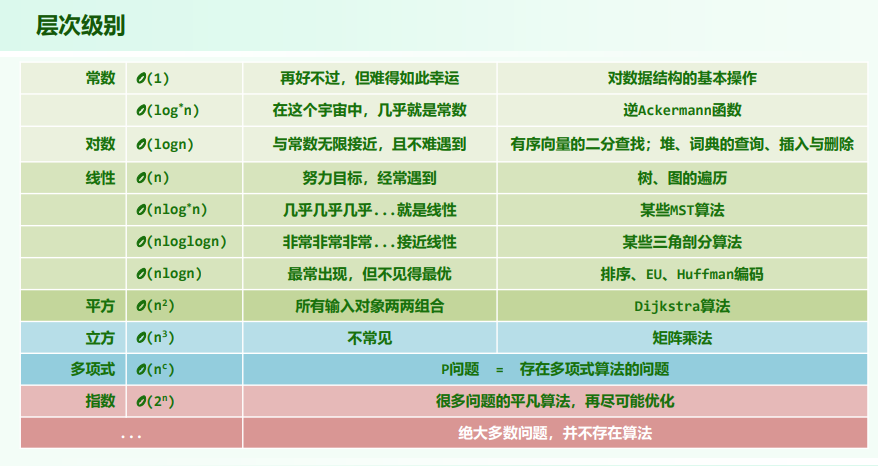
• ${\log }^{\ast }n$ 表示对数迭代函数，即取多少次对数，使得 $\log n$ 的值小于等于 1，返回的是对数运算的次数；
  • ${\log }_2^{\ast }16=3$
  • ${\log }_2^{\ast }{2}^{1024}=5:$
    • ${\log }_2{2}^{1024}=1024$,
    • ${\log }_{2}1024=10$,
    • ${\log }_{2}10\approx 3.2$,
    • ${\log }_{2}3.2\approx 1.8$,
    • ${\log }_{2}1.8<1$
  • ${\log }^{\ast }n=O({\log }^{\ast }(\log n))$

复杂度分析

级数

算术级数：与末项平方同阶

• $T(n)=1+2+...+n=\left(\genfrac{}{}{0ex}{}{n+1}{2}\right)=\frac{n(n+1)}{2}=O(n^2)$

幂方级数：比幂级数高出一阶

• $T(n)=\sum _{k=0}^n{k}^d\approx {\int }_0^n{x}^{d}dx=\frac{n^{d+1}}{d+1}=O(n^{d+1})$

几何级数：与末项同阶

• $T_a(n)=\sum _{k=0}^n=a^0+a^1+...+a^n=\frac{a^{n+1}-1}{a-1}=O(a^n),1<a$
• 即等比数列求和

收敛： 收敛级数：$O(1)$

• $\sum _{k=2}^n\frac{1}{(k-1)\cdot k}=\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+...+\frac{1}{(n-1)\cdot n}=1-\frac{1}{n}=O(1)$
• $\sum _{\mathrm{k}\mathrm{is}\mathrm{a}\mathrm{perfect}\mathrm{power}}\frac{1}{k-1}=\frac{1}{3}+\frac{1}{7}+\frac{1}{8}+\frac{1}{15}+...=1=O(1)$

几何分布：$O(1)$

• $(1-\lambda )\cdot [1+2\lambda +3{\lambda }^2+4{\lambda }^3+...]=\frac{1}{1-\lambda }=O(1),0<\lambda <1$
• 举例：对于一个抛硬币实验，正面向上概率为 $\lambda$，则抛若干次至第一次出现正面向上的期望为 $(1-\lambda )\cdot [1+2\lambda +3{\lambda }^2+4{\lambda }^3+...]=\frac{1}{1-\lambda }=O(1),0<\lambda <1$

不收敛，但有限： 调和级数：$\Theta (logn)$

• $h(n)=\sum _{k=1}^n\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+...=\ln n+\gamma +O(\frac{1}{2n})=\Theta (\log n)$

对数级数：$\Theta (nlogn)$

• $\sum _{k=1}^n\ln k=\ln \prod _{k=1}^n=\ln (n!)\approx (n+0.5)\ln n-n=\Theta (n\log n)$
• stirling formulation: $n!\approx \sqrt{2\pi n}\cdot (\frac{n}{e}{)}^n$
• stirling approximation: $\ln (n!)=n\ln n-n+O(\ln n)$

迭代

习题集结论

1-9 证明 $\log n=O(n^{\epsilon })$

对任何 $\epsilon >0$，都有 $\log n=O(n^{\epsilon })$

证明：

• 函数 $\ln n$ 增长得极慢，故总存在 $M>0$，使得 $n>M$ 之后总有 $\ln n<\epsilon n$。
• 令 $N=e^M$，则当 $n>N$（即 $\ln n>M$）之后，总有：$\ln (\ln n)<\epsilon \ln n$，亦即：$\ln n<n^{\epsilon }$。

1-10 等差等比之和的 O-notation

等差级数之和与其中最大项的平方同阶：

• 考查首项为常数 x、公差为常数 d > 0、长度为 n 的等差级数： $\{x,x+d,x+2d,...,x+(n-1)d\}$
• 其中末项 $(n-1)d=\Theta (n)$，各项总和为： $(\frac{d}{2})n^2+(x-\frac{d}{2})n=\Theta (n^2)$。

等比级数之和与最大项同阶：

• 考查首项为常数 x、公比为常数 d > 1、长度为 n 的等比级数： $\{x,xd,x{d}^2,...,x{d}^{n-1}\}$
• 其中末项 $x{d}^{n-1}=\Theta (d^n)$，各项总和为： $x(d^n-1)/(d-1)=\Theta (d^n)$

算法导论中排序渐进增长率的题

迭代与递归

减治

线性递归跟踪

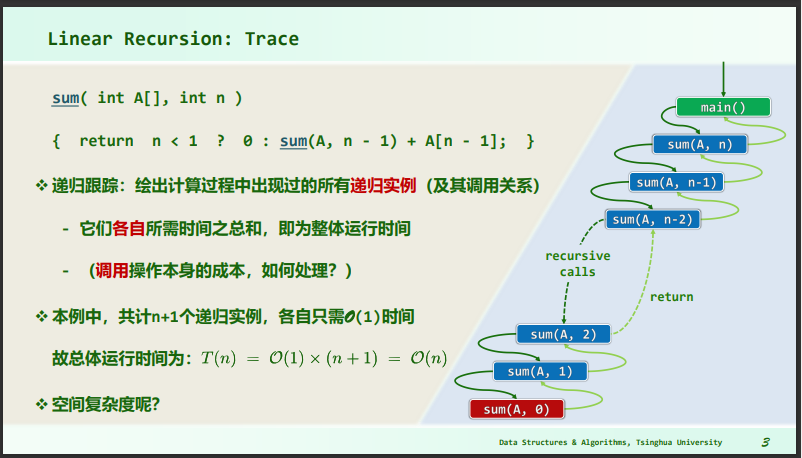
• 跟踪递归发生了多少次，每次递归占用了多少空间、运行了多少时间，即可计算整体时间复杂度
• 该问题中空间复杂度为 $O(n)$；

线性递推方程

• 减治的思想是，每一次操作都将问题规模减小一部分，被减小的平凡部分时间复杂度是固定的 $O(1)$ 或其它，然后递推下去；

分治

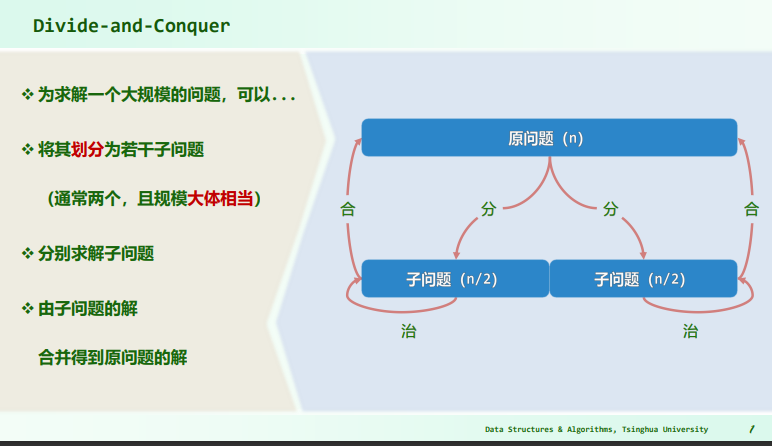
• 二分查找是减治，归并排序是分治；
  • 减治思想是除去平凡的子问题；
  • 而分治思想是将原问题切分成若干子问题，对子问题进行同样的操作，直到子问题变为平凡；

二分递归跟踪

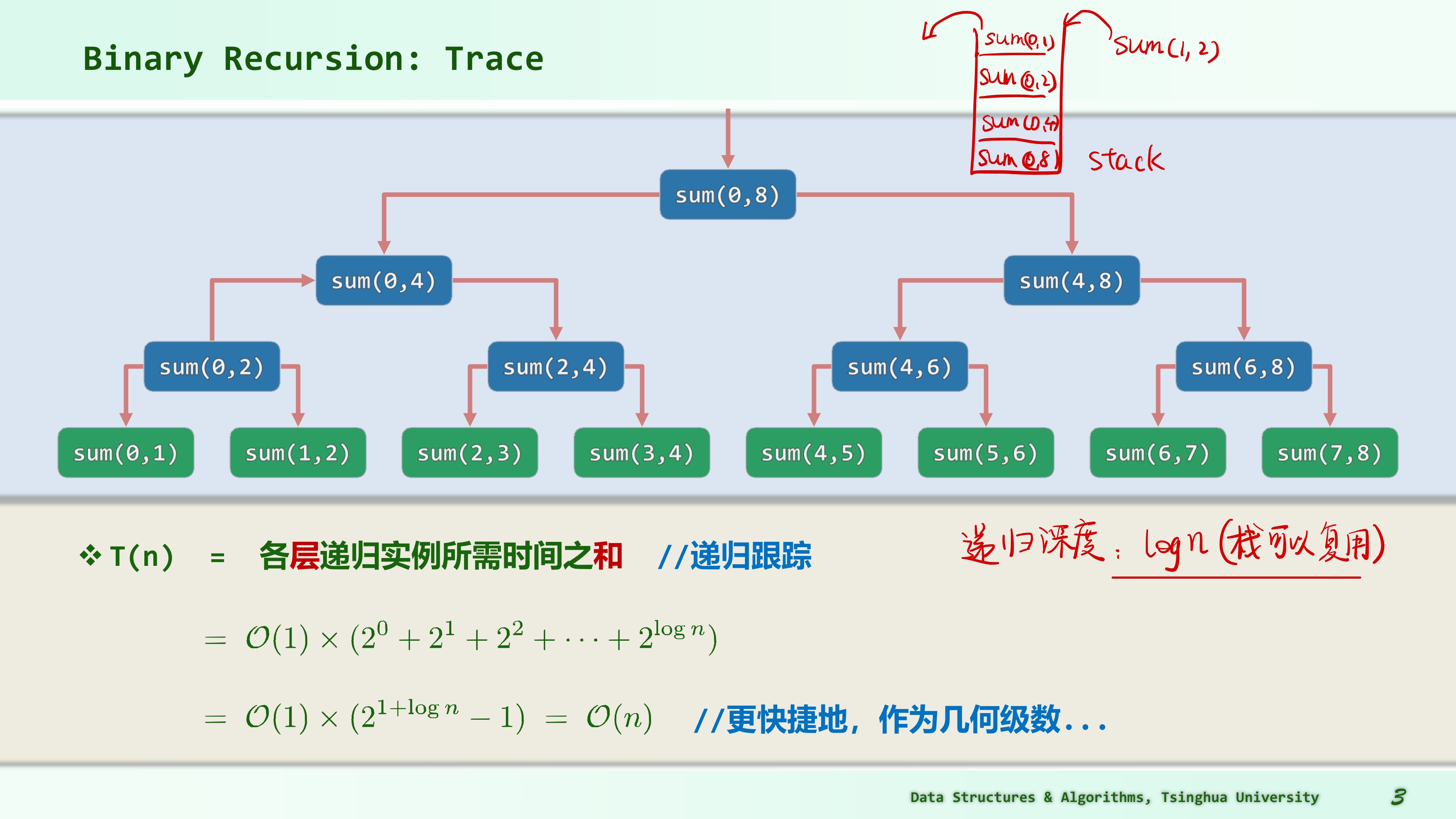
• sum (0,8) 先入栈，接着是 sum (0,4)，接着是 sum (0,2)，最后是 sum (0,1)，此时栈顶为平凡地返回 A[0]，出栈后 sum (1,2) 入栈得到 A[1]，出栈后栈顶变为 sum (0,2) 则得到 sum (0,1)+sum (1,2)=A[0]+A[1]，以此类推；
• 递归深度为 $\log n$；

二分递推方程

$$\begin{array}{rl}& T(n)=2\cdot T(\frac{n}{2})+O(1)\\ & ...\\ & T(1)=O(1)//递归基:sum(A,k,k)\end{array}$$

求解：

$$\begin{array}{rl}T(n)& =2\cdot T(\frac{n}{2})+O(1)\\ & =4\cdot T(\frac{n}{4})+O(3)\\ & =8\cdot T(\frac{n}{8})+O(7)\\ & ...\\ & =n\cdot T(1)+O(n-1)\\ & =O(2n-1)\\ & =O(n)\end{array}$$

判断题：关于减治和分治的区分

判断: 用分治思想来解决长度为 n 的数组求和问题 (n 足够大), 递归实例的数目会比用减治的方法少. (❌)

解析:

• 减冶算法中递归实例分别是: 1 个规模为 n 的实例, 1 个规模为 n-1 的实例, 1 个规模为 n-2 的实例, … 共 n 个；
• 分治算法中, 递归实例分别是: 1 个规模为 n 的实例, 2 个规模为 $\frac{n}{2}$ 的实例, 4 个规模为 $\frac{n}{4}$ 的实例, 共有 1 + 2 + 4 + … + n 个。

主定理

Generic form

Master Theorem 是一种用于分析递归算法时间复杂度的工具，特别适用于分治算法中的递归情况。这些算法将输入划分为大小相等的较小子问题，递归求解子问题，然后组合子问题解决方案以给出原始问题的解决方案。这种算法的时间可以通过将它们在递归的顶层执行的工作（将问题划分为子问题，然后组合子问题解决方案）与算法的递归调用中所做的时间相加来表示。

以下内容来自 Wikipedia：Master theorem (analysis of algorithms)

Master Theorem的一般形式如下：

如果递归算法的递归式可以表示为：$T(n)=aT(\frac{n}{b})+f(n)$，其中：

• $n$ is the size of an input problem
• $a$ is the number of subproblems in the recursion,
• $b$ is the factor by which the subproblem size is reduced in each recursive call (b>1), (a、b 不能与 n 相关)
• $f(n)$ denotes the amount of time taken at the top level of the recurrence. Another word, $f(n)$ is the time to create the subproblems and combine their results in the above procedure.

Recurrences of this form often satisfy one of the three following regimes, based on how the work to split/recombine the problem $f(n)$ relates to the critical exponent $c_{crit}={\log }_{b}a=\frac{\log (\#\text{subproblems})}{\log (\text{relative subproblem size)}}$.

Case 1

Work to split/recombine a problem is dwarfed by subproblems. (recursion tree is leaf-heavy. )

• 如果 $f(n)=O(n^c),c<c_{crit}$ (upper-bounded by a lesser exponent polynomial)，
• 那么 $T(n)=\Theta (n^{c_{crit}})$, The splitting term does not appear; the recursive tree structure dominates.
• i.e. If $b=a^2$ and $f(n)=O(n^{\frac{1}{2}-ϵ})$, then $T(n)=\Theta (n^{\frac{1}{2}})$.

Case 2

Work to split/recombine a problem is comparable to subproblems.

• 如果 $f(n)=\Theta (n^{c_{crit}}\times {\log }^{k}n),k\ge 0$，(rangebound by the critical-exponent polynomial, times zero or more optional $\log s$.)
• 那么 $T(n)=\Theta (n^{c_{crit}}\times {\log }^{(k+1)}n)$，(The bound is splitting term, where the $\log$ is augmented by a single power.)
• i.e. If $b=a^2$ and $f(n)=\Theta (n^{\frac{1}{2}})$, then $T(n)=\Theta (n^{\frac{1}{2}}\log n)$
• i.e. If $b=a^2$ and $f(n)=\Theta (n^{\frac{1}{2}}\log n)$, then $T(n)=\Theta (n^{\frac{1}{2}}{\log }^{2}n)$.

Extension of Case 2 handles all values of $k$

1. When $f(n)=\Theta (n^{c_{crit}}{\log }^{k}n)$ for any $k>-1$,

• then $T(n)=\Theta (n^{c_{crit}}{\log }^{k+1}n)$. (The bound is the splitting term, where the $\log$ is augmented by a single power.)
• i.e. if $b=a^2$ and $f(n)=\Theta (n^{\frac{1}{2}}\times {\log }^{-\frac{1}{2}}n)$, then $T(n)=\Theta (n^{\frac{1}{2}}{\log }^{\frac{1}{2}}n)$.

2. When $f(n)=\Theta (n^{c_{crit}}{\log }^{k}n)$ for any $k=-1$,

• then $T(n)=\Theta (n^{c_{crit}}\log \log n)$. (The bound is the splitting term, where the $\log$ reciprocal is replaced by an iterated $\log$.)
• i.e. if $b=a^2$ and $f(n)=\Theta (n^{\frac{1}{2}}\times {\log }^{-1}n)$, then $T(n)=\Theta (n^{\frac{1}{2}}\log \log n)$.

3. When $f(n)=\Theta (n^{c_{crit}}{\log }^{k}n)$ for any $k<-1$,

• then $T(n)=\Theta (n^{c_{crit}})$. (The bound is the splitting term, where the $\log$ is disappears.)
• i.e. if $b=a^2$ and $f(n)=\Theta (n^{\frac{1}{2}}\times {\log }^{-2}n)$, then $T(n)=\Theta (n^{\frac{1}{2}})$.

Case 3

Work to split/recombine a problem dominates subproblems. (recursion tree is root-heavy. )

• 如果 $f(n)=\Omega (n^c),c>c_{crit}$ (lower-bounded by a greater-exponent polynomial)，且存在 $k<1$，使得 $af(\frac{n}{b})\le kf(n)$ (the second condition is called regularity condition)，
• 那么 $T(n)=\Theta (f(n))$ (total is dominated by the splitting term $f(n)$.)
• i.e. if $b=a^2$ and $f(n)=\Omega (n^{\frac{1}{2}+ϵ})$ and the regularity condition holds, then $T(n)=\Theta (f(n))$.

Example

Case 1：

$$T(n)=8T\left(\frac{n}{2}\right)+1000n^2$$

As one can see from the formula above:

a=8,\,b=2,\,f(n)=1000n^{2} $$, so

f(n) = O\left(n^c\right) $$, where $c=2$.

Next, we see if we satisfy the case 1 condition:

$${\log }_{b}a={\log }_{2}8=3>c$$

It follows from the first case of the master theorem that

$$T(n)=\Theta \left(n^{{\log }_{b}a}\right)=\Theta \left(n^3\right)$$

(This result is confirmed by the exact solution of the recurrence relation, which is $T(n)=1001n^3-1000n^2$, assuming $T(1)=1$).

Case 2

$$T(n)=2T\left(\frac{n}{2}\right)+10n$$

As we can see in the formula above the variables get the following values:

$$a=2,b=2,c=1,f(n)=10n$$ f(n)=\Theta \left(n^{c}\log ^{k}n\right) $$ where $c=1,k=0$. Next, we see if we satisfy the case 2 condition:

\log _{b}a=\log _{2}2=1

and therefore, c and $\displaystyle \log _{b}a$ are equal. So it follows from the second case of the master theorem:

T(n)=\Theta \left(n^{\log _{b}a}\log ^{k+1}n\right)=\Theta \left(n^{1}\log ^{1}n\right)=\Theta \left(n\log n\right)

Thus the given recurrence relation $T(n)$ was in $\Theta(n \log n)$. (This result is confirmed by the exact solution of the recurrence relation, which is $T(n)=n+10n\log _{2}n$, assuming $T(1)=1$). #### Case 3

T(n)=2T\left({\frac {n}{2}}\right)+n^{2}

$$Aswecanseeintheformulaabovethevariablesgetthefollowingvalues:$$

a=2,,b=2,,f(n)=n^{2}

f(n)=\Omega \left(n^{c}\right) $$, where $c=2$.

Next, we see if we satisfy the case 3 condition:

\log _{b}a=\log _{2}2=1 $$, and therefore, yes,

c>\log _{b}a

$$Theregularityconditionalsoholds:$$

2\left({\frac {n^{2}}{4}}\right)\leq kn^{2} $$, choosing $k=\frac{1}{2}$.

So it follows from the third case of the master theorem:

$$T\left(n\right)=\Theta \left(f(n)\right)=\Theta \left(n^2\right)$$

Thus the given recurrence relation $T(n)$ was in $\Theta (n^2)$, that complies with the $f(n)$ of the original formula.

(This result is confirmed by the exact solution of the recurrence relation, which is $T(n)=2n^2-n$, assuming $T(1)=1$)

Inadmissible equations

The following equations cannot be solved using the master theorem:

• $T(n)=2^{n}T\left(\frac{n}{2}\right)+n^n$， $a$ is not a constant; the number of subproblems should be fixed.

• $T(n)=2T\left(\frac{n}{2}\right)+\frac{n}{\log n}$， non-polynomial difference between $f(n)$ and $n^{{\log }_{b}a}$ (see below; extended version applies)

• $T(n)=0.5T\left(\frac{n}{2}\right)+n$， $a<1$ cannot have less than one sub problem.

• $T(n)=64T\left(\frac{n}{8}\right)-n^2\log n$， $f(n)$, which is the combination time, is not positive

• $T(n)=T\left(\frac{n}{2}\right)+n(2-\cos n)$， case 3 but regularity violation.

In the second inadmissible example above, the difference between $f(n)$ and $n^{{\log }_{b}a}$ can be expressed with the ratio $\frac{f(n)}{n^{{\log }_{b}a}}=\frac{n/\log n}{n^{{\log }_{2}2}}=\frac{n}{n\log n}=\frac{1}{\log n}$. It is clear that $\frac{1}{\log n}<n^{ϵ}$ for any constant $ϵ>0$. Therefore, the difference is not polynomial and the basic form of the Master Theorem does not apply. The extended form (case 2b) does apply, giving the solution $T(n)=\Theta (n\log \log n)$.

Application

Algo	Recurrence relationship	Run time	Comment
Binary Search	$T(n)=T(\frac{n}{2})+O(1)$	$O(\log n)$	Apply Master theorem case $c={\log }_{b}a$, where $a=1,b=2,c=0,k=0$
Binary Tree Traversal	$T(n)=2T(\frac{n}{2})+O(1)$	$O(n)$	Apply Master theorem case $c<{\log }_{b}a$ where $a=2,b=2,c=0$
Merge Sort	$T(n)=2T(\frac{n}{2})+O(n)$	$O(n\log n)$	Apply Master theorem case $c={\log }_{b}a$ where $a=2,b=2,c=1,k=0$

迭代与递归应用：总和最大区段

从整数数列中找出总和最大的区段（有多个时，短者、靠后者优先）。

蛮力

递增策略

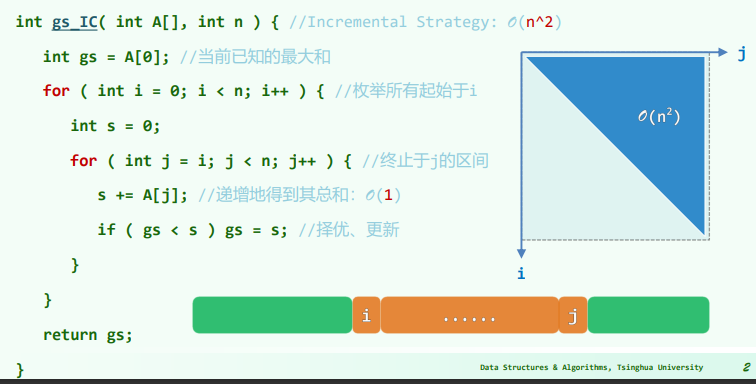
1. 首先，代码定义了一个变量 gs，用于存储当前已知的最大和，初始值为序列的第一个元素 A[0]。
2. 外层循环使用变量 i 枚举所有可能的起始位置。这个循环将从序列的第一个元素开始，依次遍历到序列的最后一个元素。
3. 在内层循环中，使用变量 j 从当前起始位置 i 开始遍历到序列的末尾。在这个循环中，定义了一个变量 s 用于累计当前区段的和。
4. 对于每个 j，将序列中的元素 A[j] 加到变量 s 中，从而递增地计算当前区段的总和。这个操作的时间复杂度是 O(1)，因为每次只需进行一次加法。
5. 在每次计算完区段的和后，代码比较 gs（当前已知的最大和）与 s（当前区段的和）。如果 s 更大，则更新 gs 为 s，从而保持 gs 始终存储最大的连续区段和。
6. 继续循环，内层循环将覆盖所有可能的终止位置，并计算以每个可能的起始位置 i 开始的连续区段的最大和。
7. 外层循环的结束后，gs 将包含整个序列中总和最大的连续区段的和，函数返回这个值作为结果。

分治

递推公式得：

$$T(n)=2T(\frac{n}{2})+O(n)+O(1)$$

减治

考查最短的总和非正后缀 $A[k,hi)$，以及总和最大区段 $GS(lo,hi)=A[i,j)$ ，如下：

• 非正数 (负数和 0)不会是 GS 的前缀；

这段代码使用了一个循环来处理整数序列 A，以寻找总和最大的连续区段。下面逐步解释代码的执行过程：

1. 首先，代码定义了三个变量：gs 用于存储当前已知的最大和，初始值为序列的第一个元素 A[0]；s 用于累计当前区段的和，初始值为 0；i 用于追踪当前处理的元素位置，初始值为序列的长度 n。
2. 使用 while 循环，条件是 0 < i--，这表示从序列的末尾向开始位置逐步遍历。循环将在当前区间内进行操作，区间的起始位置在 i 处。
3. 在循环中，将当前元素 A[i] 加到变量 s 中，从而递增地累计当前区段的总和。
4. 接着，代码比较 gs（当前已知的最大和）与 s（当前区段的和）。如果 s 更大，则更新 gs 为 s，从而保持 gs 始终存储最大的连续区段和。
5. 然后，代码检查变量 s 的值是否小于等于 0。如果是，说明当前区段的和已经为负数或零，这时将变量 s 重置为 0。这是减治策略的关键步骤，因为负和的后缀对于整体和的增加没有贡献，所以可以将这部分”剪除”。
6. 继续循环，逐步向序列的起始位置移动，同时更新 s 和 gs 的值。
7. 循环结束后，变量 gs 将包含整个序列中总和最大的连续区段的和，函数返回这个值作为结果。

这种减治策略的思路相对于递增策略具有更好的时间复杂度，为 $O(n)$，因为它只需一次遍历即可找到最大连续区段和。这是因为在遍历过程中，通过每次比较和重置 s 的方式，有效地剪除了负和的后缀，从而保证了在连续区段和变得负数之后能够重新开始寻找可能的更大区段和。

动态规划

求 fib(n)

递归法求 fib(n) 的复杂度：

• 递归深度/空间复杂度 $O(n)$

递归法低效的原因在于，递归实例被重复调用多次，先后出现的递归实例达到 $O({\Phi }^n)$ 个，而实际上递归实例的种类不过 $O(n)$ 种。

若能记忆递归实例计算的结果，保存沿途信息，使得后续不必再重复计算，即可降低无用计算。 动态规划——颠倒计算方向，将自顶向下的递归改为自底向上的迭代。

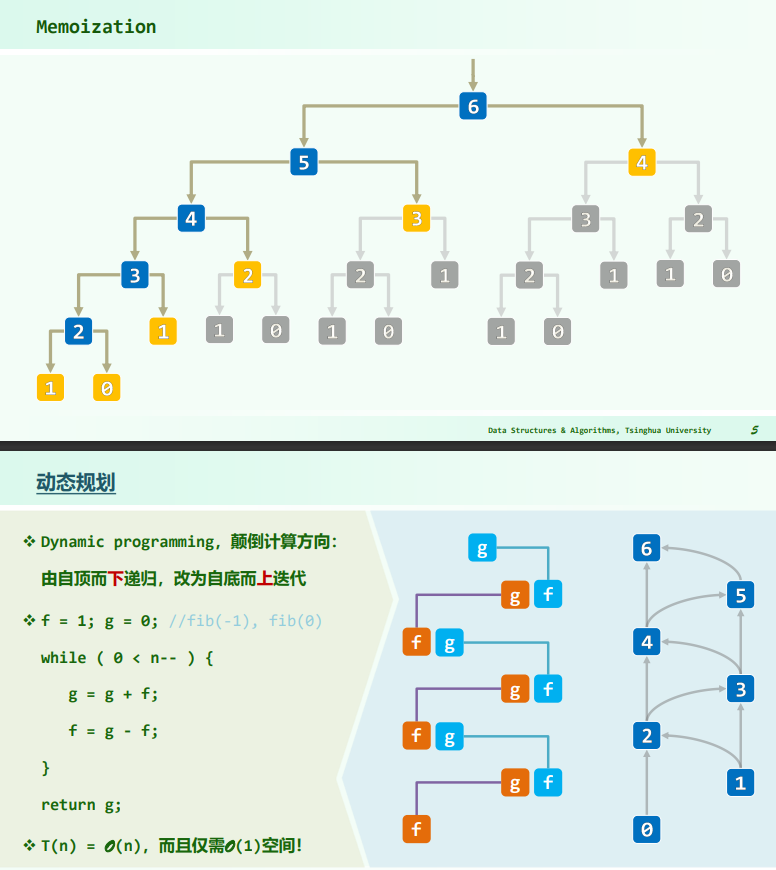
• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

最长公共子序列

• 子序列：原序列中若干字符，按原相对次序构成，不必连续；

递归

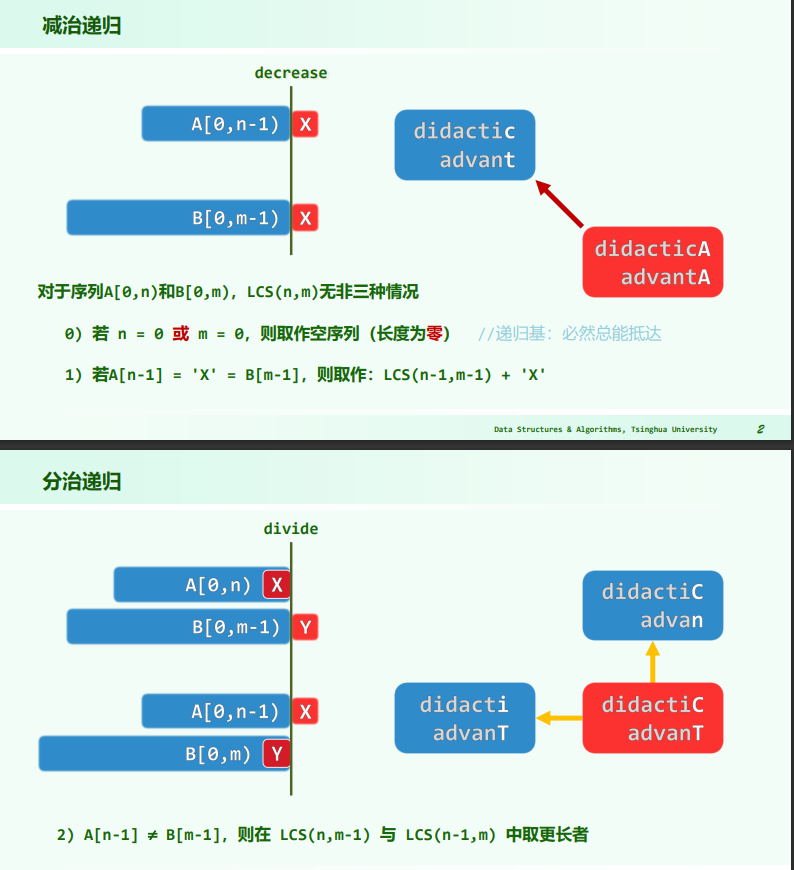
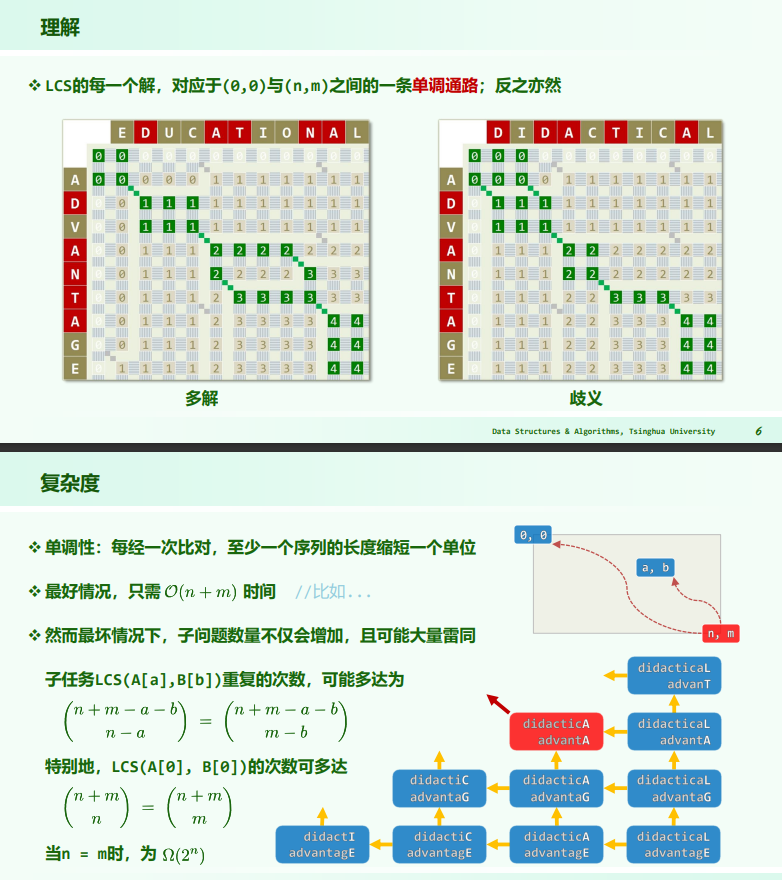
当两个字符序列 A 和 B 的内容相似度很低，即它们在大部分位置上没有相同的字符，且长度较长时，递归法求解最长公共子序列问题会陷入最坏情况。最坏情况发生在每次递归调用都需要进行两个分支，即分别调用 lcs(A, n-1, B, m) 和 lcs(A, n, B, m-1)，这会产生大量的重复实例，导致算法的时间复杂度急剧增加。

假设有两个字符序列：

• A: ABCDEFGHIJKLMNOPQRSTUVWXYZ
• B: abcdefghijklmnopqrstuvwxyz

在这个例子中，序列 A 包含大写字母，序列 B 包含小写字母，它们之间没有相同的字符。这意味着无论怎样的子序列都不会同时出现在两个序列中。因此，在这种情况下，每次递归调用都会产生两个分支，即 lcs(A, n-1, B, m) 和 lcs(A, n, B, m-1)，并且这两个分支的递归调用也会继续以相同的方式进行，直到序列的长度减少到 0。

考虑其中一个分支，比如 lcs(A, n-1, B, m)，这个分支将继续产生类似的分支，一直到 n 减少到 0。而另一个分支 lcs(A, n, B, m-1) 也会以相同的方式进行。这种情况下，递归调用会产生大量的重复计算，导致时间复杂度急剧上升。

动态规划

// 记忆化版
unsigned int lcsMemo(char const* A, int n, char const* B, int m) {
	unsigned int *lcs = new unsigned int[n*m]; //lookup-table of sub-solutions
	memset(lcs, 0xFF, sizeof(unsigned int)*n*m); //initialized with n*m UINT_MAX's
	unsigned int solu = lcsM(A, n, B, m, lcs, m);
	delete[] lcs;
	return solu;
}
unsigned int lcsM( char const * A, int n, char const * B, int m,
unsigned int * const lcs, int const M ) {
	if (n < 1 || m < 1) return 0; //trivial cases
	if (UINT_MAX != lcs[(n-1)*M + m-1]) return lcs[(n-1)*M + m-1]; //recursion stops
	else return lcs[(n-1)*M + m-1] = (A[n-1] == B[m-1]) ? 1 + lcsM(A, n-1, B, m-1, lcs, M) : max( lcsM(A, n-1, B, m, lcs, M), lcsM(A, n, B, m-1, lcs, M) );
}

这段代码实现了一个优化过的最长公共子序列（LCS）算法，使用记忆化（也称为动态规划的自顶向下方法）来保存已计算过的子问题的解，从而避免重复计算，提高了算法的效率.

1. lcsMemo 函数是主函数，它初始化了一个大小为 n * m 的查找表（lcs），用于存储子问题的解。这个表的每个元素 lcs[i][j] 表示字符串 A 的前 i 个字符与字符串 B 的前 j 个字符之间的最长公共子序列长度。
2. memset 函数用于将 lcs 表的所有元素初始化为无效值 UINT_MAX，表示这些子问题的解尚未计算过。
3. lcsM 函数是一个递归辅助函数，用于实际计算最长公共子序列的长度，并使用记忆化来避免重复计算。
4. 在 lcsM 函数中，首先检查基本情况，即如果 n 或 m 小于 1，则返回 0，因为这表示一个空串的最长公共子序列长度为 0。
5. 接着，通过查找 lcs 表，判断是否已经计算过当前子问题的解。如果已经计算过，就直接返回该解，从而避免了重复计算。
6. 如果当前子问题的解尚未计算过，那么进入递归的计算过程。如果当前 A 的第 n-1 个字符等于 B 的第 m-1 个字符，则将问题划分为更小的子问题：计算 A 的前 n-1 个字符与 B 的前 m-1 个字符之间的最长公共子序列长度，并在其基础上加上 1。
7. 如果当前字符不相等，那么问题被划分为两个子问题：计算 A 的前 n-1 个字符与 B 的前 m 个字符之间的最长公共子序列长度，以及计算 A 的前 n 个字符与 B 的前 m-1 个字符之间的最长公共子序列长度。然后，取这两个子问题解的较大值。
8. 在计算子问题的解后，将其保存到 lcs 表中，以便以后的查询，避免了对同一子问题的重复计算。
9. 主函数 lcsMemo 在调用 lcsM 函数时传入了 lcs 表，以便在递归过程中保存已计算过的子问题的解。最终，主函数返回整个序列的最长公共子序列长度。

这种优化方法通过避免重复计算显著提高了算法的效率，将时间复杂度从指数级别（递归法）降低到了线性时间复杂度 $O(n\times m)$。

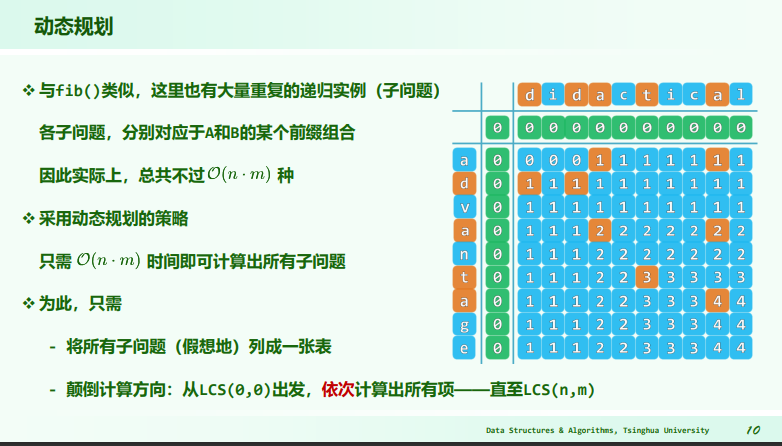
// 从底向上的迭代法DP
unsigned int lcs(char const * A, int n, char const * B, int m) {
	if (n < m) { swap(A, B); swap(n, m); } //make sure m <= n
	unsigned int* lcs1 = new unsigned int[m+1]; //the current two rows are
	unsigned int* lcs2 = new unsigned int[m+1]; //buffered alternatively
	memset(lcs1, 0x00, sizeof(unsigned int) * (m+1));
	memset(lcs2, 0x00, sizeof(unsigned int) * (m+1));
	for (int i = 0; i < n; swap(lcs1, lcs2), i++)
		for (int j = 0; j < m; j++)
			lcs2[j+1] = (A[i] == B[j]) ? 1 + lcs1[j] : max(lcs2[j], lcs1[j+1]);
	unsigned int solu = lcs1[m]; 
	delete[] lcs1; 
	delete[] lcs2; 
	return solu;
}

这段代码是使用迭代方法实现的动态规划来计算最长公共子序列（LCS）。相较于之前的递归法，这种迭代方法是自底向上地构建了一个二维数组（或表格）来存储子问题的解，从而避免了递归过程中的重复计算。

1. 首先，代码会检查 n 和 m 的大小关系，以确保 m 小于等于 n。这是因为动态规划的思路中，会使用两个数组来保存当前行和前一行的 LCS 值，以交替更新。为了减小空间复杂度，始终选择较短的字符串作为列。
2. 然后，代码创建了两个大小为 m + 1 的数组 lcs1 和 lcs2，用于存储当前行和前一行的LCS值。
3. 通过 memset 函数，将 lcs1 和 lcs2 数组初始化为全零。
4. 使用两个嵌套的循环，外层循环遍历字符串 A，内层循环遍历字符串 B。
5. 在循环中，根据动态规划的思想，计算 lcs2[j + 1]，即当前位置 (i, j) 处的LCS值。这是根据以下两种情况来计算的：
   • 如果 A[i] 等于 B[j]，则说明这两个字符可以贡献到LCS，所以 lcs2[j + 1] 将等于 1 + lcs1[j]，其中 lcs1[j] 表示上一行前一列的LCS值。
   • 如果 A[i] 不等于 B[j]，则需要在 lcs2[j]（当前行前一列的LCS值）和 lcs1[j + 1]（上一行当前列的LCS值）之间选择较大的值，因为当前字符不匹配，LCS值保持不变。
6. 每次内层循环结束时，lcs2 数组将更新为当前行的LCS值。
7. 外层循环结束后，整个 lcs1 数组中的最后一个元素即为最终结果，它表示字符串 A 和字符串 B 的最长公共子序列长度。
8. 最后，释放之前分配的内存，即 lcs1 和 lcs2 数组。

番外

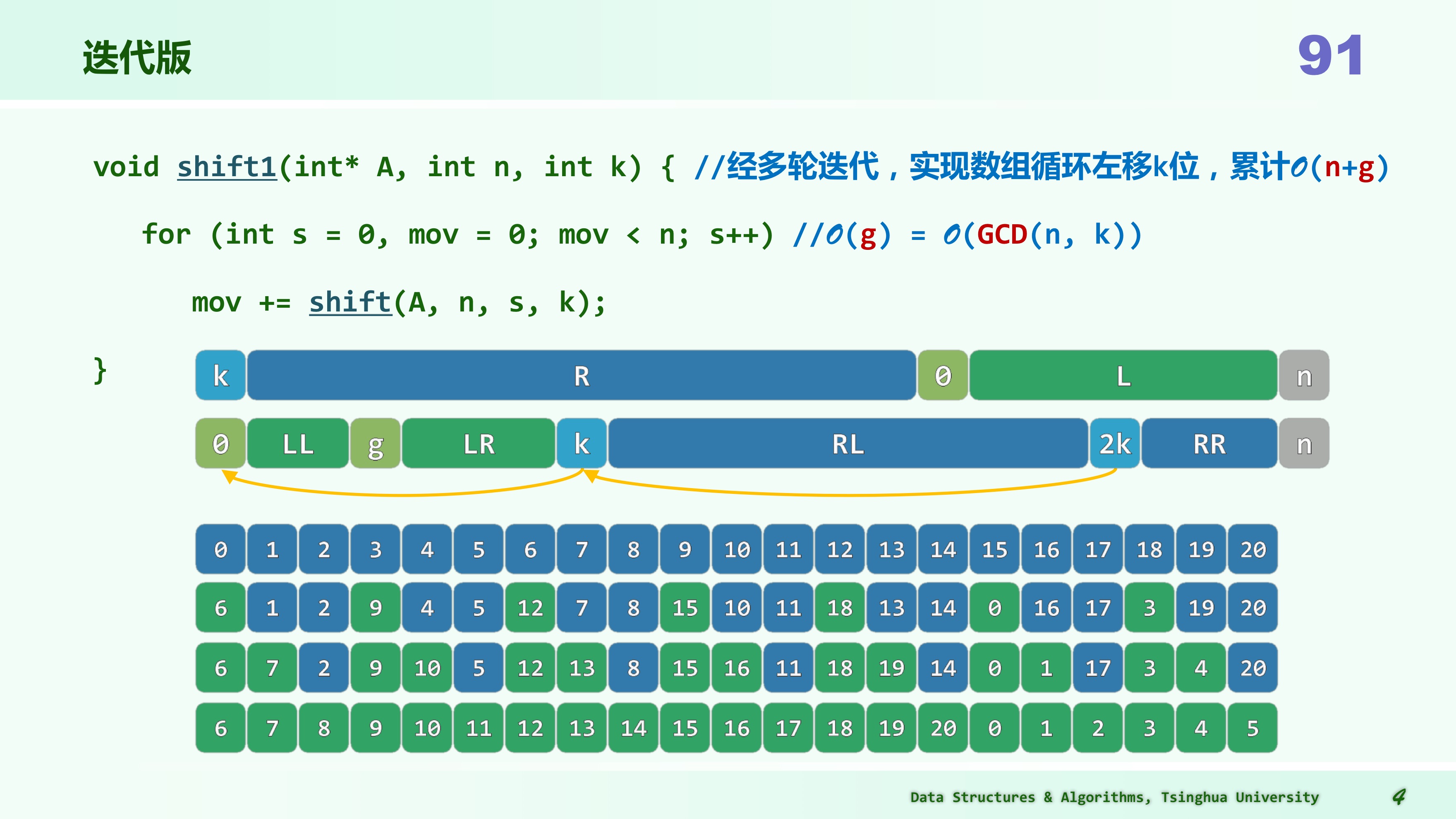
局限 1: 缓存——就地循环位移

要求：仅用 $O(1)$ 辅助空间，将数组 A[0, n) 中的元素向左循环移动 k 个单元。

BF 版

迭代版

int shift(int *A, int n, int s, int k)
{
	// O(n/gcd(n,k))
	int b=A[s];
	int i=s,j=(s+k)%n;
	int mov=0; // mov记录移动的次数
	while(s!=j){
		// 从A[s]出发，以k为间隔，依次左移k位
		A[i]=A[j];
		i=j;
		j=(j+k)%n;
		mov++;
	}
	A[i]=b;
	return mov+1; // 最后起始元素转入对应位置
}//[0,n)由关于k的gcd(n,k)个同余类组成，shift(s,k)能够且只能够使其中之一就位
 
void shift1(int *A,int n,int k){
	//O(n+g)
	for(int s=0,mov=0;mov<n;s++){
		//O(g)=O(gcd(n,k))
		mov+=shift(A,n,s,k);
	}
}

1. shift 函数：
   • 首先，它保存了起始位置s处的元素到变量b中。
   • 然后，使用两个指针i和j来表示当前位置和目标位置（根据间隔k计算得到）。
   • 接下来，使用一个循环来依次将元素从位置j移动到位置i，同时更新i和j，直到s等于j，即回到起始位置。
   • 最后，将保存在b中的元素赋值给i位置，完成循环位移。同时，返回移动的次数mov+1。
   • 时间复杂度：循环的次数取决于 gcd(n, k)，因为 gcd(n, k)代表了在进行循环位移时需要遍历的同余类的数量。因此时间复杂度为 $O(\frac{n}{gcd(n,k)})$。
2. shift1 函数：
   • 在这个函数中，使用了一个循环来调用 shift 函数，每次从不同的起始位置s开始进行循环位移，直到所有元素都移动到合适的位置。
   • 时间复杂度：总共进行了n次 shift 操作，每个 shift 操作的时间复杂度为$O(\frac{n}{gcd(n,k)})$，所以总体时间复杂度为$O(\frac{n^2}{gcd(n,k)})$。

同余类

同余类：在模运算中，如果两个整数 a 和 b 除以一个正整数 m 的余数相同，即 (a % m) = (b % m)，那么 a 和 b 被称为在模 m 下是同余的。这意味着它们在模 m 的情况下具有相同的剩余值。 例如，考虑模 5 的情况

• 7 % 5 = 2
• 12 % 5 = 2

在模 5 下，7 和 12 是同余的，因为它们的余数都是 2。

现在让回到循环位移问题。在这个问题中，将一个数组 A 中的元素按照指定的间隔 k 进行循环位移。这意味着你从某个位置 s 开始，然后按照间隔 k 将元素移到新的位置。这个过程一直持续，直到回到起始位置 s。

为了理解时间复杂度涉及到同余类的原因，考虑以下情况：

• 数组长度为 n。
• 间隔 k。

数组的长度 n 和间隔 k 之间的最大公约数（gcd）决定了需要多少次循环才能回到起始位置。这是因为在每次循环中，按照间隔 k 将元素移动，直到回到起始位置。如果 n 和 k 的 gcd 是 1，那么需要 n 次循环才能回到起始位置，因为每次移动都会导致一个新的位置。如果 n 和 k 的 gcd 大于 1，那么需要更少的循环次数，因为多个位置属于同一个同余类。

举例来说，假设 n=8 和 k=2：

• gcd (8, 2) = 2

在这种情况下，只需要 4 次循环就能回到起始位置，因为每次移动都会将元素移到同一个同余类中的位置。

因此，时间复杂度与 gcd (n, k)有关，因为 gcd (n, k)代表了需要遍历的同余类的数量，它决定了循环的次数。如果 gcd (n, k)等于 1，时间复杂度可能达到 O (n)，但如果 gcd (n, k)大于 1，时间复杂度会更低，因为你需要更少的循环操作。

倒置版

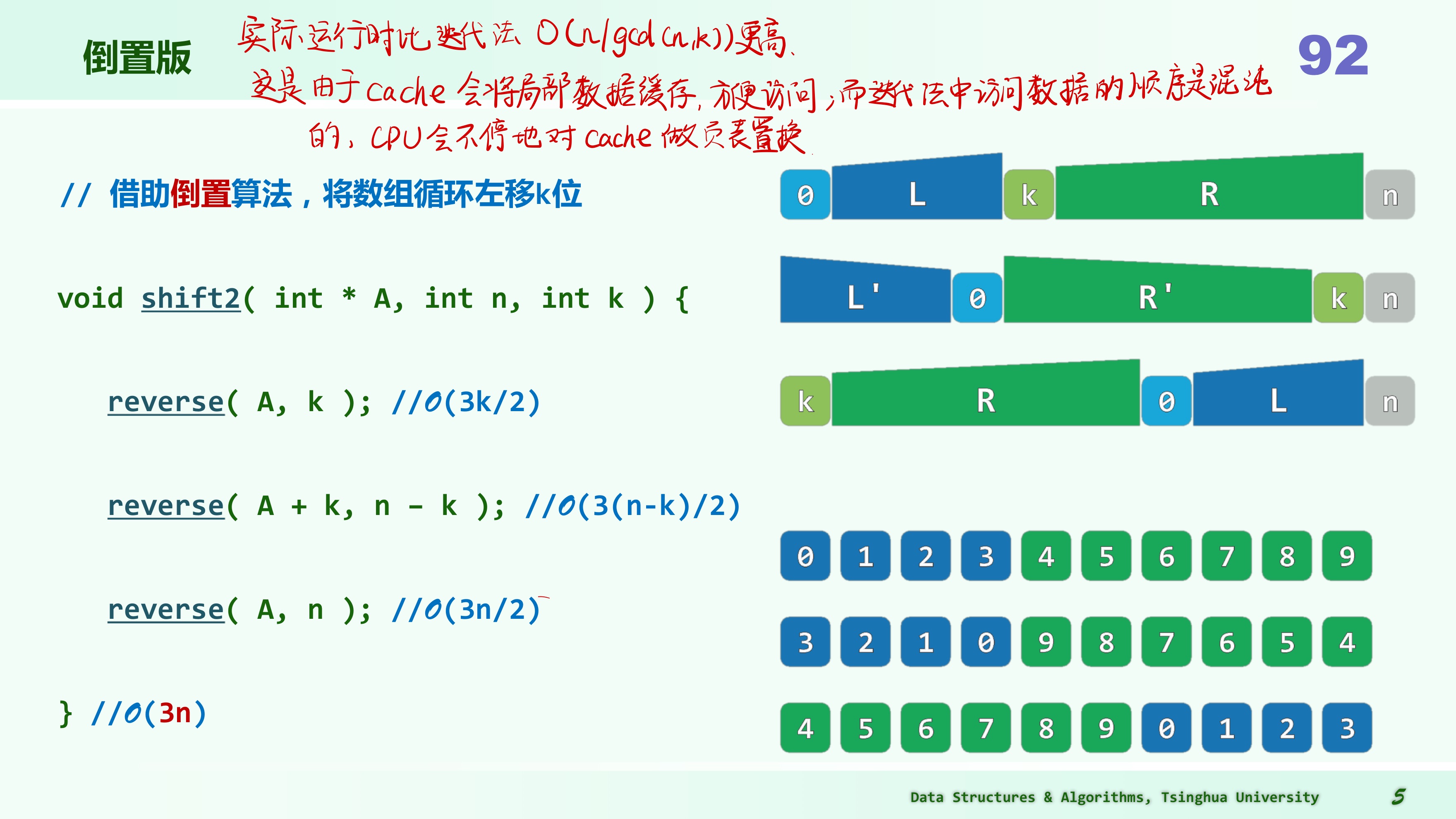
void reverse(int *A,int lo,int hi){
	//数组倒置递归版
	if(lo<hi){
		swap(A[lo],A[hi]);
		reverse(A,lo+1,hi-1);
	}// else 隐含了两种递归基
}// O(hi-lo+1)
 
void reverse(int *A,int lo,int hi){
	//数组倒置迭代版1
next: //算法起始位置添加跳转标志
	if ( lo < hi ) {
		swap( A[lo], A[hi] ); //交换A[lo]和A[hi]
		lo++; hi--; //收缩待倒置区间
		goto next; //跳转至算法体的起始位置，迭代地倒置A(lo, hi)
	} //else隐含了迭代的终止
}//O(hi-lo+1)

该算法的迭代版本有可能只需更少的交换操作，故单就此指标而言，似乎更加“优于”以上版本。然而就实际的计算效率而言，以上版本却要远远优于其它版本。

究其原因在于，reverse() 之类的操作所涉及的数据元素，在物理上是连续分布的，因此操作系统的缓存机制可以轻易地被激活，并充分发挥作用；其它版本的交换操作尽管可能更少，但数据元素在空间往往相距很远，甚至随机分布，缓存机制将几乎甚至完全失效。

在实际的算法设计与编程中，这些方面也是首先必须考虑的因素；在当下，面对规模日益膨胀的大数据，这方面的技巧对算法的实际性能更是举足轻重。

局限 2: 字宽

输入规模，准确地定义应为——用以描述输入所需的空间规模。思考计算 $powe{r}_a(n)=a^n$，其迭代法代码如下：

pow=1;//O(1)
while(0<n){//O(n)
	pow *= a;
	n--; //O(2)
}

这个计算直接推算时间复杂度，是 $T(n)=1+2n=O(n)$，这是以 $n$ 本身的数值作为输入规模考量，似乎没问题，算法到达了最优。

真的如此吗？实际上，此类计算中若以输入指数 $n$ 的二进制位数 $r=1+\lfloor {\log }_{2}n\rfloor$ 作为输入规模，则运行时间为 $O(2^r)$，显然，算法还有优化的潜力。

从 $O(n)$ 到 $O(r=\log n)$

int power(int a,int n){
	//迭代版
	int pow=1,p=a; //O(1)
	while(0<n){ //O(logn)
		if(n & 1) //O(1)
			pow *= p; // O(1)
		n>>=1; //O(1)
		p*=p; //O(1)
	}
	return pow; //O(1)
}
 

1. int pow = 1, p = a;：初始化两个变量，pow 用于保存结果，初始为1，p 用于保存底数 a 的不断平方的结果，初始为 a。
2. while (n > 0)：使用一个循环，只要n大于0，就执行下面的操作。
3. if (n & 1)：这个条件检查n的最低位是否为1，如果是1，就将结果乘以p。这是因为如果n的二进制表示的最低位是1，那么$a^n$可以拆分为$a\ast a^{(n-1)}$，而如果最低位是0，可以拆分为$a^{\frac{n}{2}}\ast a^{\frac{n}{2}}$，这正是这个算法的核心。
4. n >>= 1：将n右移一位，相当于将n除以2，这是因为在每一步中，都在将指数减小一半。
5. p *= p：将底数p平方，因为在每一步中，都在将底数p不断平方。
6. 最后，返回 pow，即最终的计算结果。

这个优化版代码的关键思想在于通过二进制分解指数 $n$，将计算复杂度从 $O(n)$ 降低到 $O(\log n)$ 。它的核心观察是利用了指数 $n$ 的二进制表示，如果 $n$ 的某一位是 1，就将对应的底数 $a$ 的幂累积到结果中，然后将 $n$ 右移一位，将指数减小一半，同时底数 $a$ 不断平方。这个方法明显更高效，特别是在计算大指数的情况下。

inline int sqr(int a){return a*a;}
int power(int a,int n){
	//递归版
	if(0==n) return 1;//递归基，否则视n的奇偶分别递归
	else{
		if(n&1){
			return sqr(power(a,n>>1))<<1;
		}else{
			return sqr(power(a,n>>1));
		}	
	}
} // O(logn)=O(r),r为输入指数n的比特位数

悖论？

上面算法可以在 $O(\log n)$ 时间内计算出 $powe{r}_a(n)=a^n$，但是 $a^n$ 的二进制展开宽度为 $\Theta (n)$，这意味着即使是直接打印 $a^n$ 也需要至少 $\Omega (n)$ 的时间。

哪里错了？

1. 常数代价原则 (Uniform Cost Criterion)：这个原则指出，对于算法的分析，我们通常会关注计算中最昂贵（最耗时）的操作，而忽略较低阶或常数因子的操作。在计算复杂度分析中，我们关注的是算法的渐近行为，即随着输入规模的增加，计算时间的增长趋势。这意味着，即使输入规模 n 较大，只要计算某一步的代价是 O (1)，我们可以将其视为常数时间，不会对渐近复杂度产生重大影响。

2. 对数代价原则 (Logarithmic Cost Criterion)：这个原则强调了对数时间复杂度的重要性。如果一个算法的计算步骤随着输入规模 n 的增加而以对数方式增加（如 $O(\log n)$），那么它在大规模问题上的性能会比线性增长（$O(n)$）的算法好得多，即使在小规模问题上，它可能因为常数因子较大而不如线性算法。

现在来解释为什么这个悖论实际上不存在：

• 计算 $a^n$ 的二进制展开确实需要 $\Theta (n)$ 的时间，但这并不意味着我们必须显式计算每一位的二进制展开并执行相应的乘法操作。在实际的计算机算术中，使用的是更高效的算法，如快速幂算法（也称为指数的二分法），它的时间复杂度是 $O(\log n)$。这意味着我们能够以对数级别的成本来计算 $a^n$，而不需要逐位计算。
• 在常数代价原则的背景下，虽然 $a^n$ 的二进制展开宽度为 $\Theta (n)$，但计算 $a^n$ 的代价并不是逐位计算，而是通过快速幂算法将指数 $n$ 分解为对数级别的子问题。因此，每个子问题的代价是 $O(1)$，虽然有多个子问题，但总的计算时间仍然是 $O(\log n)$，这符合对数代价原则。

因此，尽管 $a^n$ 的二进制展开宽度较大，但我们可以使用高效的算法在 $O(\log n)$ 时间内计算 $a^n$，而这并不违反常数代价原则或对数代价原则。这个悖论实际上是由于算法的高效性和渐近分析的原则相结合而产生的。

局限 3: 随机数

任给一个数组，理想地将其中元素次序随机打乱：

void shuffle(int A[],int n){
	while (1<n) swap(A[rand()%n],A[--n]);
}

这段代码使用了 Fisher-Yates shuffle 算法来将数组内所有元素的次序随机打乱。该算法是一个经典的洗牌算法，可以等概率地生成所有 $n!$ 中的排列，前提是 rand() 函数生成的随机数是均匀分布的，且不会出现重复的随机数。

让我们来分析一下为什么这个算法能够生成等概率的排列：

1. 在每次循环迭代中，从未被处理的元素中随机选择一个元素（通过 rand() % n），并与当前尚未处理的最后一个元素（A[--n]）交换位置。

2. 通过这种方式，每个元素都有机会成为数组的当前区间最后一个元素，而每个元素被选中的概率是相等的，因为 rand() 函数通常会产生均匀分布的随机数。

3. 当所有元素都被处理（n 变为 1）时，洗牌过程完成。

由于每个元素都有机会在每一轮中被选为最后一个元素，最终生成的排列是等概率的。这是因为每个元素被选中的概率是 1/n，其中 n 是剩余未处理元素的数量。

关于该问题，可以详细阅读下一章的内容：习题 2-6：permute 生成随机排列 和 18-Fisher-Yates-shuffle 。

习题请看： 11-Intro-Exercise 。