Introduction
A B+ tree is an advanced form of a self-balancing tree in which all the values are present in the leaf level.
An important concept to be understood before learning B+ tree is multilevel indexing. In multilevel indexing, the index of indices is created as in figure below. It makes accessing the data easier and faster.
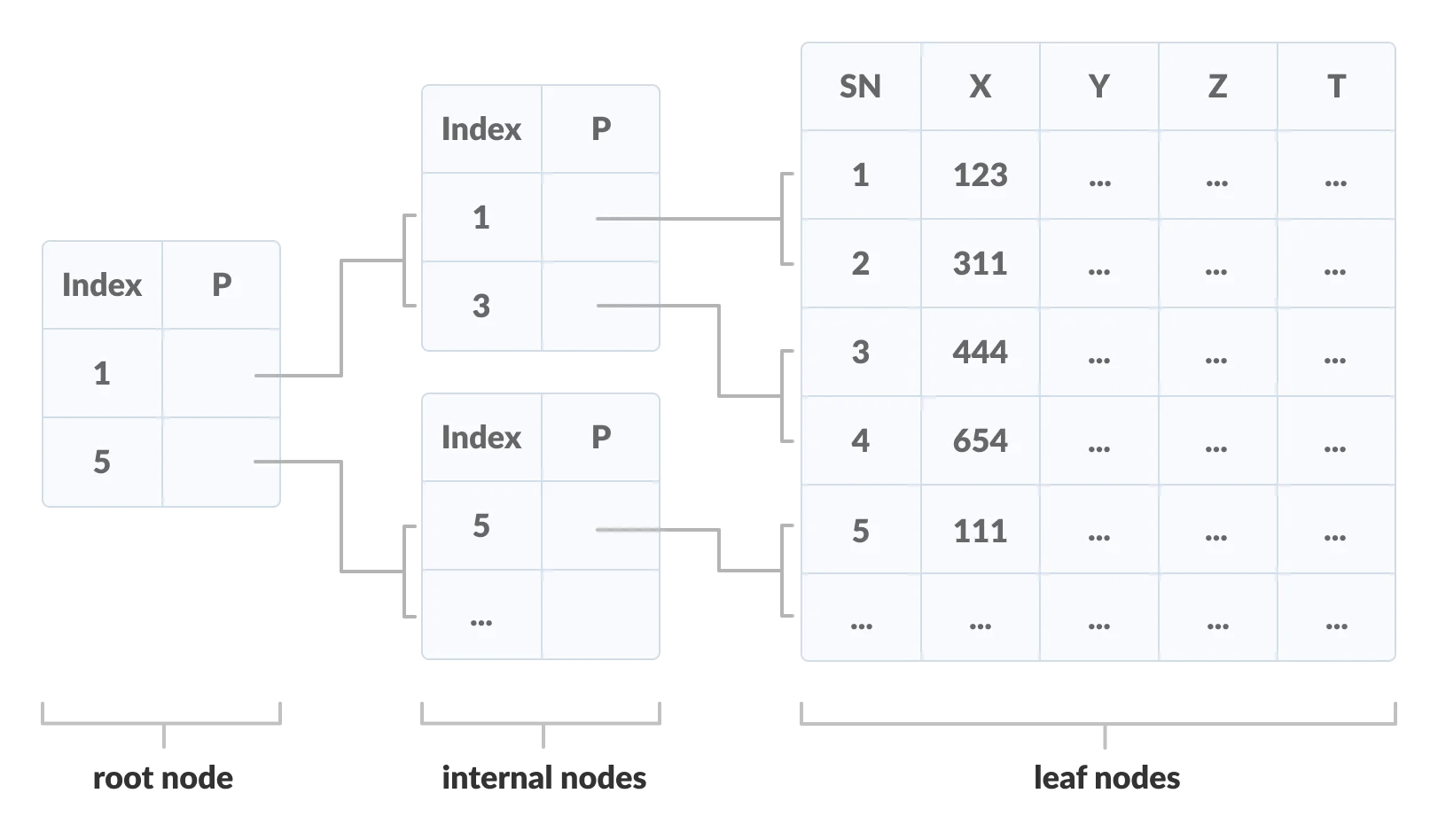
Properties of a B+ Tree
- All leaves are at the same level.
- The root has at least two children.
- Each node except root can have a maximum of
mchildren and at leastm/2children. - Each node can contain a maximum of
m - 1keys and a minimum of⌈m/2⌉ - 1keys.
Comparison with BTree
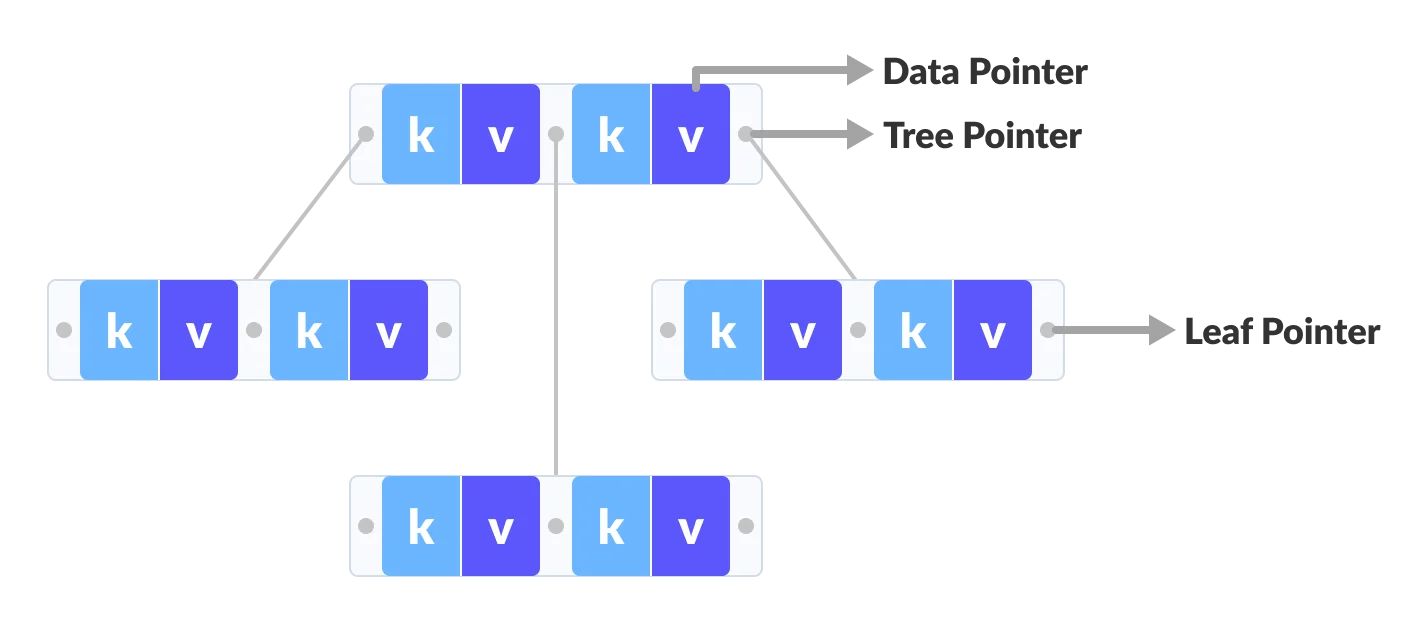
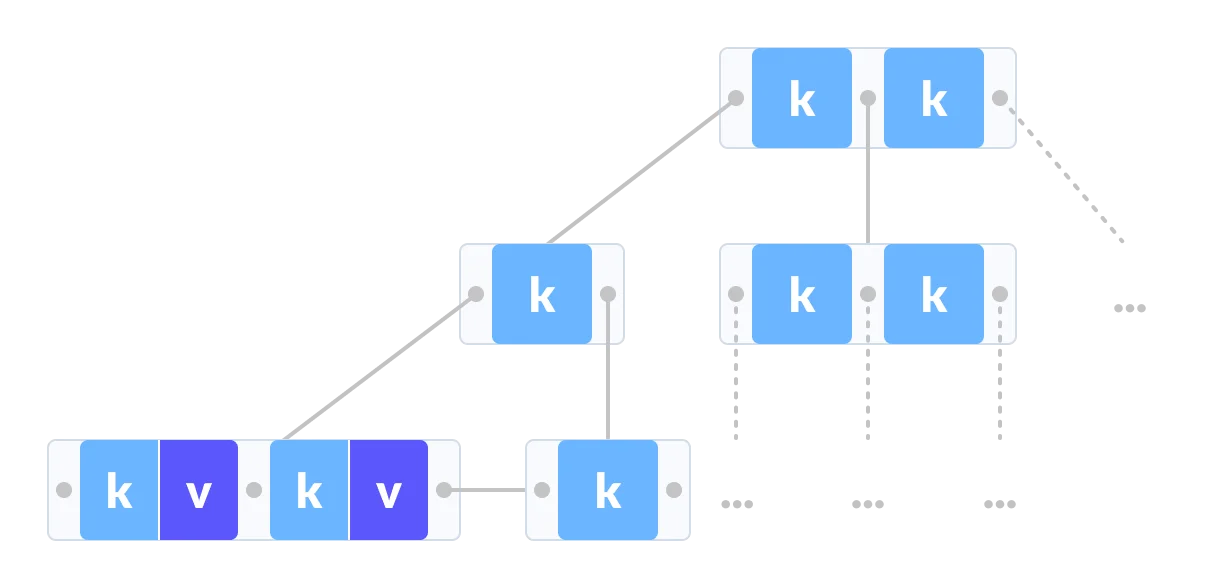
The data pointers are present only at the leaf nodes on a B+ tree whereas the data pointers are present in the internal, leaf or root nodes on a B-tree.
The leaves are not connected with each other on a B-tree whereas they are connected on a B+ tree.
Operations on a B+ tree are faster than on a B-tree.
B+ Tree Applications
- Multilevel Indexing
- Faster operations on the tree (insertion, deletion, search)
- Database indexing
Searching
The following steps are followed to search for data in a B+ Tree of order m. Let the data to be searched be k.
- Start from the root node. Compare
kwith the keys at the root node[k1, k2, k3,......km - 1]. - If
k < k1, go to the left child of the root node. - Else if
k == k1, comparek2. Ifk < k2,klies betweenk1andk2. So, search in the left child ofk2. - If
k > k2, go fork3,k4,…km-1as in steps 2 and 3. - Repeat the above steps until a leaf node is reached.
- If
kexists in the leaf node, return true else return false.
Example
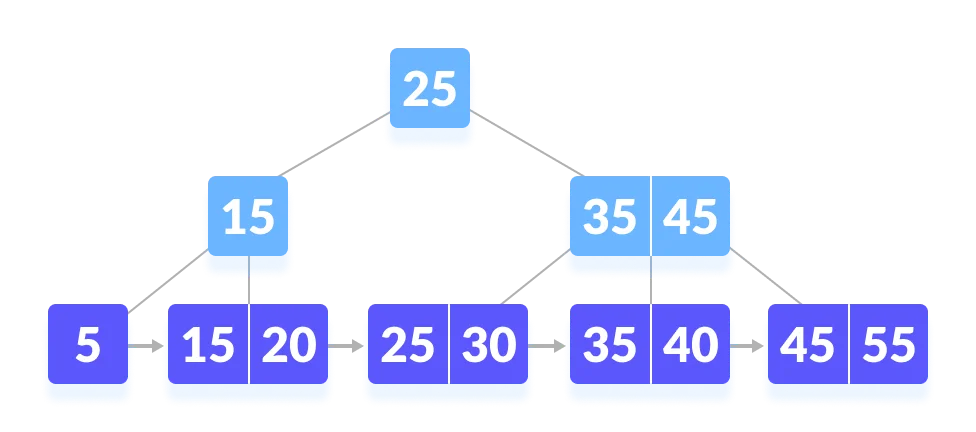
Let us search k = 45 on the following B+ tree.
-
Compare
kwith the root node.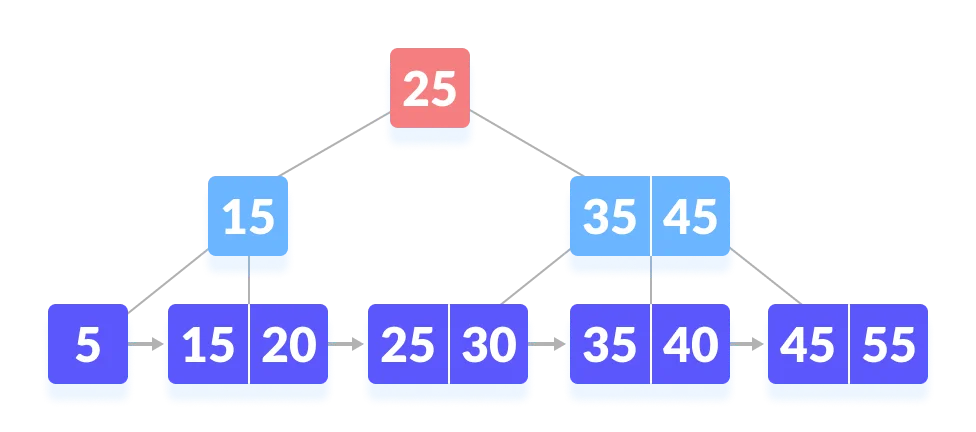
-
Since
k>25, go to the right child.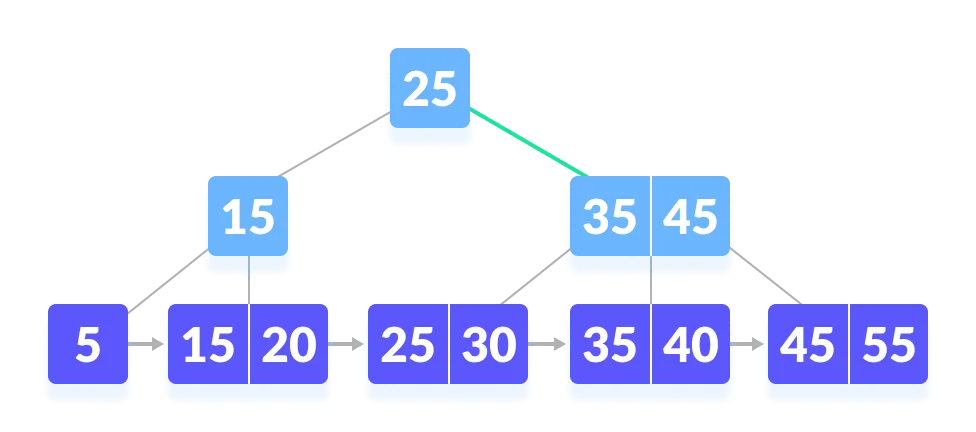
-
Compare
kwith 35. Sincek>35, comparekwith 45.
-
Since
k>=45, so go to the right child.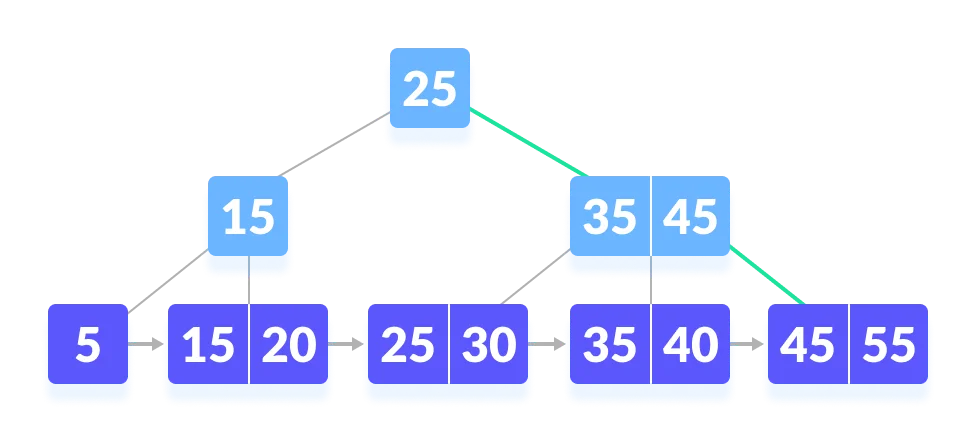
-
kis found.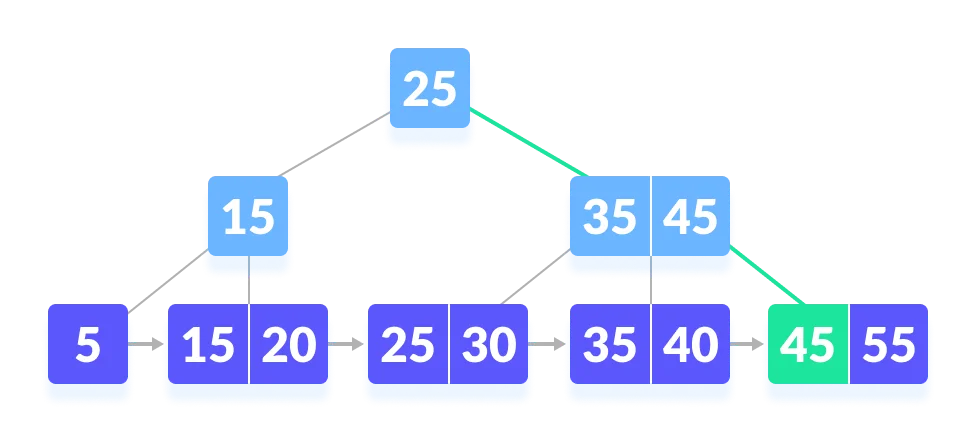
Implementation
in python
# B+ tee in python
import math
# Node creation
class Node:
def __init__(self, order):
self.order = order
self.values = []
self.keys = []
self.nextKey = None
self.parent = None
self.check_leaf = False
# Insert at the leaf
def insert_at_leaf(self, leaf, value, key):
if (self.values):
temp1 = self.values
for i in range(len(temp1)):
if (value == temp1[i]):
self.keys[i].append(key)
break
elif (value < temp1[i]):
self.values = self.values[:i] + [value] + self.values[i:]
self.keys = self.keys[:i] + [[key]] + self.keys[i:]
break
elif (i + 1 == len(temp1)):
self.values.append(value)
self.keys.append([key])
break
else:
self.values = [value]
self.keys = [[key]]
# B plus tree
class BplusTree:
def __init__(self, order):
self.root = Node(order)
self.root.check_leaf = True
# Insert operation
def insert(self, value, key):
value = str(value)
old_node = self.search(value)
old_node.insert_at_leaf(old_node, value, key)
if (len(old_node.values) == old_node.order):
node1 = Node(old_node.order)
node1.check_leaf = True
node1.parent = old_node.parent
mid = int(math.ceil(old_node.order / 2)) - 1
node1.values = old_node.values[mid + 1:]
node1.keys = old_node.keys[mid + 1:]
node1.nextKey = old_node.nextKey
old_node.values = old_node.values[:mid + 1]
old_node.keys = old_node.keys[:mid + 1]
old_node.nextKey = node1
self.insert_in_parent(old_node, node1.values[0], node1)
# Search operation for different operations
def search(self, value):
current_node = self.root
while(current_node.check_leaf == False):
temp2 = current_node.values
for i in range(len(temp2)):
if (value == temp2[i]):
current_node = current_node.keys[i + 1]
break
elif (value < temp2[i]):
current_node = current_node.keys[i]
break
elif (i + 1 == len(current_node.values)):
current_node = current_node.keys[i + 1]
break
return current_node
# Find the node
def find(self, value, key):
l = self.search(value)
for i, item in enumerate(l.values):
if item == value:
if key in l.keys[i]:
return True
else:
return False
return False
# Inserting at the parent
def insert_in_parent(self, n, value, ndash):
if (self.root == n):
rootNode = Node(n.order)
rootNode.values = [value]
rootNode.keys = [n, ndash]
self.root = rootNode
n.parent = rootNode
ndash.parent = rootNode
return
parentNode = n.parent
temp3 = parentNode.keys
for i in range(len(temp3)):
if (temp3[i] == n):
parentNode.values = parentNode.values[:i] + \
[value] + parentNode.values[i:]
parentNode.keys = parentNode.keys[:i +
1] + [ndash] + parentNode.keys[i + 1:]
if (len(parentNode.keys) > parentNode.order):
parentdash = Node(parentNode.order)
parentdash.parent = parentNode.parent
mid = int(math.ceil(parentNode.order / 2)) - 1
parentdash.values = parentNode.values[mid + 1:]
parentdash.keys = parentNode.keys[mid + 1:]
value_ = parentNode.values[mid]
if (mid == 0):
parentNode.values = parentNode.values[:mid + 1]
else:
parentNode.values = parentNode.values[:mid]
parentNode.keys = parentNode.keys[:mid + 1]
for j in parentNode.keys:
j.parent = parentNode
for j in parentdash.keys:
j.parent = parentdash
self.insert_in_parent(parentNode, value_, parentdash)
# Delete a node
def delete(self, value, key):
node_ = self.search(value)
temp = 0
for i, item in enumerate(node_.values):
if item == value:
temp = 1
if key in node_.keys[i]:
if len(node_.keys[i]) > 1:
node_.keys[i].pop(node_.keys[i].index(key))
elif node_ == self.root:
node_.values.pop(i)
node_.keys.pop(i)
else:
node_.keys[i].pop(node_.keys[i].index(key))
del node_.keys[i]
node_.values.pop(node_.values.index(value))
self.deleteEntry(node_, value, key)
else:
print("Value not in Key")
return
if temp == 0:
print("Value not in Tree")
return
# Delete an entry
def deleteEntry(self, node_, value, key):
if not node_.check_leaf:
for i, item in enumerate(node_.keys):
if item == key:
node_.keys.pop(i)
break
for i, item in enumerate(node_.values):
if item == value:
node_.values.pop(i)
break
if self.root == node_ and len(node_.keys) == 1:
self.root = node_.keys[0]
node_.keys[0].parent = None
del node_
return
elif (len(node_.keys) < int(math.ceil(node_.order / 2)) and node_.check_leaf == False) or (len(node_.values) < int(math.ceil((node_.order - 1) / 2)) and node_.check_leaf == True):
is_predecessor = 0
parentNode = node_.parent
PrevNode = -1
NextNode = -1
PrevK = -1
PostK = -1
for i, item in enumerate(parentNode.keys):
if item == node_:
if i > 0:
PrevNode = parentNode.keys[i - 1]
PrevK = parentNode.values[i - 1]
if i < len(parentNode.keys) - 1:
NextNode = parentNode.keys[i + 1]
PostK = parentNode.values[i]
if PrevNode == -1:
ndash = NextNode
value_ = PostK
elif NextNode == -1:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
else:
if len(node_.values) + len(NextNode.values) < node_.order:
ndash = NextNode
value_ = PostK
else:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
if len(node_.values) + len(ndash.values) < node_.order:
if is_predecessor == 0:
node_, ndash = ndash, node_
ndash.keys += node_.keys
if not node_.check_leaf:
ndash.values.append(value_)
else:
ndash.nextKey = node_.nextKey
ndash.values += node_.values
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
self.deleteEntry(node_.parent, value_, node_)
del node_
else:
if is_predecessor == 1:
if not node_.check_leaf:
ndashpm = ndash.keys.pop(-1)
ndashkm_1 = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [value_] + node_.values
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
p.values[i] = ndashkm_1
break
else:
ndashpm = ndash.keys.pop(-1)
ndashkm = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [ndashkm] + node_.values
parentNode = node_.parent
for i, item in enumerate(p.values):
if item == value_:
parentNode.values[i] = ndashkm
break
else:
if not node_.check_leaf:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [value_]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndashk0
break
else:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [ndashk0]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndash.values[0]
break
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
if not node_.check_leaf:
for j in node_.keys:
j.parent = node_
if not parentNode.check_leaf:
for j in parentNode.keys:
j.parent = parentNode
# Print the tree
def printTree(tree):
lst = [tree.root]
level = [0]
leaf = None
flag = 0
lev_leaf = 0
node1 = Node(str(level[0]) + str(tree.root.values))
while (len(lst) != 0):
x = lst.pop(0)
lev = level.pop(0)
if (x.check_leaf == False):
for i, item in enumerate(x.keys):
print(item.values)
else:
for i, item in enumerate(x.keys):
print(item.values)
if (flag == 0):
lev_leaf = lev
leaf = x
flag = 1
record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert('5', '33')
bplustree.insert('15', '21')
bplustree.insert('25', '31')
bplustree.insert('35', '41')
bplustree.insert('45', '10')
printTree(bplustree)
if(bplustree.find('5', '34')):
print("Found")
else:
print("Not found")in java
// Searching on a B+ tree in Java
import java.util.*;
public class BPlusTree {
int m;
InternalNode root;
LeafNode firstLeaf;
// Binary search program
private int binarySearch(DictionaryPair[] dps, int numPairs, int t) {
Comparator<DictionaryPair> c = new Comparator<DictionaryPair>() {
@Override
public int compare(DictionaryPair o1, DictionaryPair o2) {
Integer a = Integer.valueOf(o1.key);
Integer b = Integer.valueOf(o2.key);
return a.compareTo(b);
}
};
return Arrays.binarySearch(dps, 0, numPairs, new DictionaryPair(t, 0), c);
}
// Find the leaf node
private LeafNode findLeafNode(int key) {
Integer[] keys = this.root.keys;
int i;
for (i = 0; i < this.root.degree - 1; i++) {
if (key < keys[i]) {
break;
}
}
Node child = this.root.childPointers[i];
if (child instanceof LeafNode) {
return (LeafNode) child;
} else {
return findLeafNode((InternalNode) child, key);
}
}
// Find the leaf node
private LeafNode findLeafNode (InternalNode node, int key) {
Integer[] keys = node. keys;
int i;
for (i = 0; i < node. degree - 1; i++) {
if (key < keys[i]) {
break;
}
}
Node childNode = node. childPointers[i];
if (childNode instanceof LeafNode) {
return (LeafNode) childNode;
} else {
return findLeafNode ((InternalNode) node. childPointers[i], key);
}
}
// Finding the index of the pointer
private int findIndexOfPointer (Node[] pointers, LeafNode node) {
int i;
for (i = 0; i < pointers. length; i++) {
if (pointers[i] == node) {
break;
}
}
return i;
}
// Get the mid point
private int getMidpoint () {
return (int) Math.ceil ((this. m + 1) / 2.0) - 1;
}
// Balance the tree
private void handleDeficiency (InternalNode in) {
InternalNode sibling;
InternalNode parent = in. parent;
if (this. root == in) {
for (int i = 0; i < in. childPointers. length; i++) {
if (in. childPointers[i] != null) {
if (in. childPointers[i] instanceof InternalNode) {
this. root = (InternalNode) in. childPointers[i];
this. root. parent = null;
} else if (in. childPointers[i] instanceof LeafNode) {
this. root = null;
}
}
}
}
else if (in. leftSibling != null && in.leftSibling.isLendable ()) {
sibling = in. leftSibling;
} else if (in. rightSibling != null && in.rightSibling.isLendable ()) {
sibling = in. rightSibling;
int borrowedKey = sibling. keys[0];
Node pointer = sibling. childPointers[0];
in. keys[in. degree - 1] = parent. keys[0];
in. childPointers[in. degree] = pointer;
parent. keys[0] = borrowedKey;
sibling.removePointer (0);
Arrays.sort (sibling. keys);
sibling.removePointer (0);
shiftDown (in. childPointers, 1);
} else if (in. leftSibling != null && in.leftSibling.isMergeable ()) {
} else if (in. rightSibling != null && in.rightSibling.isMergeable ()) {
sibling = in. rightSibling;
sibling. keys[sibling. degree - 1] = parent. keys[parent. degree - 2];
Arrays.sort (sibling. keys, 0, sibling. degree);
parent. keys[parent. degree - 2] = null;
for (int i = 0; i < in. childPointers. length; i++) {
if (in. childPointers[i] != null) {
sibling.prependChildPointer (in. childPointers[i]);
in. childPointers[i]. parent = sibling;
in.removePointer (i);
}
}
parent.removePointer (in);
sibling. leftSibling = in. leftSibling;
}
if (parent != null && parent.isDeficient ()) {
handleDeficiency (parent);
}
}
private boolean isEmpty () {
return firstLeaf == null;
}
private int linearNullSearch (DictionaryPair[] dps) {
for (int i = 0; i < dps. length; i++) {
if (dps[i] == null) {
return i;
}
}
return -1;
}
private int linearNullSearch (Node[] pointers) {
for (int i = 0; i < pointers. length; i++) {
if (pointers[i] == null) {
return i;
}
}
return -1;
}
private void shiftDown (Node[] pointers, int amount) {
Node[] newPointers = new Node[this. m + 1];
for (int i = amount; i < pointers. length; i++) {
newPointers[i - amount] = pointers[i];
}
pointers = newPointers;
}
private void sortDictionary (DictionaryPair[] dictionary) {
Arrays.sort (dictionary, new Comparator<DictionaryPair>() {
@Override
public int compare (DictionaryPair o1, DictionaryPair o2) {
if (o1 == null && o2 == null) {
return 0;
}
if (o1 == null) {
return 1;
}
if (o2 == null) {
return -1;
}
return o1.compareTo (o2);
}
});
}
private Node[] splitChildPointers (InternalNode in, int split) {
Node[] pointers = in. childPointers;
Node[] halfPointers = new Node[this. m + 1];
for (int i = split + 1; i < pointers. length; i++) {
halfPointers[i - split - 1] = pointers[i];
in.removePointer (i);
}
return halfPointers;
}
private DictionaryPair[] splitDictionary (LeafNode ln, int split) {
DictionaryPair[] dictionary = ln. dictionary;
DictionaryPair[] halfDict = new DictionaryPair[this. m];
for (int i = split; i < dictionary. length; i++) {
halfDict[i - split] = dictionary[i];
ln.delete (i);
}
return halfDict;
}
private void splitInternalNode (InternalNode in) {
InternalNode parent = in. parent;
int midpoint = getMidpoint ();
int newParentKey = in. keys[midpoint];
Integer[] halfKeys = splitKeys (in. keys, midpoint);
Node[] halfPointers = splitChildPointers (in, midpoint);
in. degree = linearNullSearch (in. childPointers);
InternalNode sibling = new InternalNode (this. m, halfKeys, halfPointers);
for (Node pointer : halfPointers) {
if (pointer != null) {
pointer. parent = sibling;
}
}
sibling. rightSibling = in. rightSibling;
if (sibling. rightSibling != null) {
sibling. rightSibling. leftSibling = sibling;
}
in. rightSibling = sibling;
sibling. leftSibling = in;
if (parent == null) {
Integer[] keys = new Integer[this. m];
keys[0] = newParentKey;
InternalNode newRoot = new InternalNode (this. m, keys);
newRoot.appendChildPointer (in);
newRoot.appendChildPointer (sibling);
this. root = newRoot;
in. parent = newRoot;
sibling. parent = newRoot;
} else {
parent. keys[parent. degree - 1] = newParentKey;
Arrays.sort (parent. keys, 0, parent. degree);
int pointerIndex = parent.findIndexOfPointer (in) + 1;
parent.insertChildPointer (sibling, pointerIndex);
sibling. parent = parent;
}
}
private Integer[] splitKeys (Integer[] keys, int split) {
Integer[] halfKeys = new Integer[this. m];
keys[split] = null;
for (int i = split + 1; i < keys. length; i++) {
halfKeys[i - split - 1] = keys[i];
keys[i] = null;
}
return halfKeys;
}
public void insert (int key, double value) {
if (isEmpty ()) {
LeafNode ln = new LeafNode (this. m, new DictionaryPair (key, value));
this. firstLeaf = ln;
} else {
LeafNode ln = (this. root == null) ? this. firstLeaf : findLeafNode (key);
if (! ln.insert (new DictionaryPair (key, value))) {
ln. dictionary[ln. numPairs] = new DictionaryPair (key, value);
ln. numPairs++;
sortDictionary (ln. dictionary);
int midpoint = getMidpoint ();
DictionaryPair[] halfDict = splitDictionary (ln, midpoint);
if (ln. parent == null) {
Integer[] parent_keys = new Integer[this. m];
parent_keys[0] = halfDict[0]. key;
InternalNode parent = new InternalNode (this. m, parent_keys);
ln. parent = parent;
parent.appendChildPointer (ln);
} else {
int newParentKey = halfDict[0]. key;
ln. parent. keys[ln. parent. degree - 1] = newParentKey;
Arrays.sort (ln. parent. keys, 0, ln. parent. degree);
}
LeafNode newLeafNode = new LeafNode (this. m, halfDict, ln. parent);
int pointerIndex = ln.parent.findIndexOfPointer (ln) + 1;
ln.parent.insertChildPointer (newLeafNode, pointerIndex);
newLeafNode. rightSibling = ln. rightSibling;
if (newLeafNode. rightSibling != null) {
newLeafNode. rightSibling. leftSibling = newLeafNode;
}
ln. rightSibling = newLeafNode;
newLeafNode. leftSibling = ln;
if (this. root == null) {
this. root = ln. parent;
} else {
InternalNode in = ln. parent;
while (in != null) {
if (in.isOverfull ()) {
splitInternalNode (in);
} else {
break;
}
in = in. parent;
}
}
}
}
}
public Double search (int key) {
if (isEmpty ()) {
return null;
}
LeafNode ln = (this. root == null) ? this. firstLeaf : findLeafNode (key);
DictionaryPair[] dps = ln. dictionary;
int index = binarySearch (dps, ln. numPairs, key);
if (index < 0) {
return null;
} else {
return dps[index]. value;
}
}
public ArrayList<Double> search (int lowerBound, int upperBound) {
ArrayList<Double> values = new ArrayList<Double>();
LeafNode currNode = this. firstLeaf;
while (currNode != null) {
DictionaryPair dps[] = currNode. dictionary;
for (DictionaryPair dp : dps) {
if (dp == null) {
break;
}
if (lowerBound <= dp. key && dp. key <= upperBound) {
values.add (dp. value);
}
}
currNode = currNode. rightSibling;
}
return values;
}
public BPlusTree (int m) {
this. m = m;
this. root = null;
}
public class Node {
InternalNode parent;
}
private class InternalNode extends Node {
int maxDegree;
int minDegree;
int degree;
InternalNode leftSibling;
InternalNode rightSibling;
Integer[] keys;
Node[] childPointers;
private void appendChildPointer (Node pointer) {
this. childPointers[degree] = pointer;
this. degree++;
}
private int findIndexOfPointer (Node pointer) {
for (int i = 0; i < childPointers. length; i++) {
if (childPointers[i] == pointer) {
return i;
}
}
return -1;
}
private void insertChildPointer (Node pointer, int index) {
for (int i = degree - 1; i >= index; i--) {
childPointers[i + 1] = childPointers[i];
}
this. childPointers[index] = pointer;
this. degree++;
}
private boolean isDeficient () {
return this. degree < this. minDegree;
}
private boolean isLendable () {
return this. degree > this. minDegree;
}
private boolean isMergeable () {
return this. degree == this. minDegree;
}
private boolean isOverfull () {
return this. degree == maxDegree + 1;
}
private void prependChildPointer (Node pointer) {
for (int i = degree - 1; i >= 0; i--) {
childPointers[i + 1] = childPointers[i];
}
this. childPointers[0] = pointer;
this. degree++;
}
private void removeKey (int index) {
this. keys[index] = null;
}
private void removePointer (int index) {
this. childPointers[index] = null;
this. degree--;
}
private void removePointer (Node pointer) {
for (int i = 0; i < childPointers. length; i++) {
if (childPointers[i] == pointer) {
this. childPointers[i] = null;
}
}
this. degree--;
}
private InternalNode (int m, Integer[] keys) {
this. maxDegree = m;
this. minDegree = (int) Math.ceil (m / 2.0);
this. degree = 0;
this. keys = keys;
this. childPointers = new Node[this. maxDegree + 1];
}
private InternalNode (int m, Integer[] keys, Node[] pointers) {
this. maxDegree = m;
this. minDegree = (int) Math.ceil (m / 2.0);
this. degree = linearNullSearch (pointers);
this. keys = keys;
this. childPointers = pointers;
}
}
public class LeafNode extends Node {
int maxNumPairs;
int minNumPairs;
int numPairs;
LeafNode leftSibling;
LeafNode rightSibling;
DictionaryPair[] dictionary;
public void delete (int index) {
this. dictionary[index] = null;
numPairs--;
}
public boolean insert (DictionaryPair dp) {
if (this.isFull ()) {
return false;
} else {
this. dictionary[numPairs] = dp;
numPairs++;
Arrays.sort (this. dictionary, 0, numPairs);
return true;
}
}
public boolean isDeficient () {
return numPairs < minNumPairs;
}
public boolean isFull () {
return numPairs == maxNumPairs;
}
public boolean isLendable () {
return numPairs > minNumPairs;
}
public boolean isMergeable () {
return numPairs == minNumPairs;
}
public LeafNode (int m, DictionaryPair dp) {
this. maxNumPairs = m - 1;
this. minNumPairs = (int) (Math.ceil (m / 2) - 1);
this. dictionary = new DictionaryPair[m];
this. numPairs = 0;
this.insert (dp);
}
public LeafNode (int m, DictionaryPair[] dps, InternalNode parent) {
this. maxNumPairs = m - 1;
this. minNumPairs = (int) (Math.ceil (m / 2) - 1);
this. dictionary = dps;
this. numPairs = linearNullSearch (dps);
this. parent = parent;
}
}
public class DictionaryPair implements Comparable<DictionaryPair> {
int key;
double value;
public DictionaryPair (int key, double value) {
this. key = key;
this. value = value;
}
public int compareTo (DictionaryPair o) {
if (key == o.key) {
return 0;
} else if (key > o.key) {
return 1;
} else {
return -1;
}
}
}
public static void main (String[] args) {
BPlusTree bpt = null;
bpt = new BPlusTree (3);
bpt.insert (5, 33);
bpt.insert (15, 21);
bpt.insert (25, 31);
bpt.insert (35, 41);
bpt.insert (45, 10);
if (bpt.search (15) != null) {
System.out.println ("Found");
} else {
System.out.println ("Not Found");
}
;
}
}in c
// Searching on a B+ Tree in C
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// Default order
#define ORDER 3
typedef struct record {
int value;
} record;
// Node
typedef struct node {
void **pointers;
int *keys;
struct node *parent;
bool is_leaf;
int num_keys;
struct node *next;
} node;
int order = ORDER;
node *queue = NULL;
bool verbose_output = false;
// Enqueue
void enqueue(node *new_node);
// Dequeue
node *dequeue(void);
int height(node *const root);
int pathToLeaves(node *const root, node *child);
void printLeaves(node *const root);
void printTree(node *const root);
void findAndPrint(node *const root, int key, bool verbose);
void findAndPrintRange(node *const root, int range1, int range2, bool verbose);
int findRange(node *const root, int key_start, int key_end, bool verbose,
int returned_keys[], void *returned_pointers[]);
node *findLeaf(node *const root, int key, bool verbose);
record *find(node *root, int key, bool verbose, node **leaf_out);
int cut(int length);
record *makeRecord(int value);
node *makeNode(void);
node *makeLeaf(void);
int getLeftIndex(node *parent, node *left);
node *insertIntoLeaf(node *leaf, int key, record *pointer);
node *insertIntoLeafAfterSplitting(node *root, node *leaf, int key,
record *pointer);
node *insertIntoNode(node *root, node *parent,
int left_index, int key, node *right);
node *insertIntoNodeAfterSplitting(node *root, node *parent,
int left_index,
int key, node *right);
node *insertIntoParent(node *root, node *left, int key, node *right);
node *insertIntoNewRoot(node *left, int key, node *right);
node *startNewTree(int key, record *pointer);
node *insert(node *root, int key, int value);
// Enqueue
void enqueue(node *new_node) {
node *c;
if (queue == NULL) {
queue = new_node;
queue->next = NULL;
} else {
c = queue;
while (c->next != NULL) {
c = c->next;
}
c->next = new_node;
new_node->next = NULL;
}
}
// Dequeue
node *dequeue(void) {
node *n = queue;
queue = queue->next;
n->next = NULL;
return n;
}
// Print the leaves
void printLeaves(node *const root) {
if (root == NULL) {
printf("Empty tree.\n");
return;
}
int i;
node *c = root;
while (!c->is_leaf)
c = c->pointers[0];
while (true) {
for (i = 0; i < c->num_keys; i++) {
if (verbose_output)
printf("%p ", c->pointers[i]);
printf("%d ", c->keys[i]);
}
if (verbose_output)
printf("%p ", c->pointers[order - 1]);
if (c->pointers[order - 1] != NULL) {
printf(" | ");
c = c->pointers[order - 1];
} else
break;
}
printf("\n");
}
// Calculate height
int height(node *const root) {
int h = 0;
node *c = root;
while (!c->is_leaf) {
c = c->pointers[0];
h++;
}
return h;
}
// Get path to root
int pathToLeaves(node *const root, node *child) {
int length = 0;
node *c = child;
while (c != root) {
c = c->parent;
length++;
}
return length;
}
// Print the tree
void printTree(node *const root) {
node *n = NULL;
int i = 0;
int rank = 0;
int new_rank = 0;
if (root == NULL) {
printf("Empty tree.\n");
return;
}
queue = NULL;
enqueue(root);
while (queue != NULL) {
n = dequeue();
if (n->parent != NULL && n == n->parent->pointers[0]) {
new_rank = pathToLeaves(root, n);
if (new_rank != rank) {
rank = new_rank;
printf("\n");
}
}
if (verbose_output)
printf("(%p)", n);
for (i = 0; i < n->num_keys; i++) {
if (verbose_output)
printf("%p ", n->pointers[i]);
printf("%d ", n->keys[i]);
}
if (!n->is_leaf)
for (i = 0; i <= n->num_keys; i++)
enqueue(n->pointers[i]);
if (verbose_output) {
if (n->is_leaf)
printf("%p ", n->pointers[order - 1]);
else
printf("%p ", n->pointers[n->num_keys]);
}
printf("| ");
}
printf("\n");
}
// Find the node and print it
void findAndPrint(node *const root, int key, bool verbose) {
node *leaf = NULL;
record *r = find(root, key, verbose, NULL);
if (r == NULL)
printf("Record not found under key %d.\n", key);
else
printf("Record at %p -- key %d, value %d.\n",
r, key, r->value);
}
// Find and print the range
void findAndPrintRange(node *const root, int key_start, int key_end,
bool verbose) {
int i;
int array_size = key_end - key_start + 1;
int returned_keys[array_size];
void *returned_pointers[array_size];
int num_found = findRange(root, key_start, key_end, verbose,
returned_keys, returned_pointers);
if (!num_found)
printf("None found.\n");
else {
for (i = 0; i < num_found; i++)
printf("Key: %d Location: %p Value: %d\n",
returned_keys[i],
returned_pointers[i],
((record *)
returned_pointers[i])
->value);
}
}
// Find the range
int findRange(node *const root, int key_start, int key_end, bool verbose,
int returned_keys[], void *returned_pointers[]) {
int i, num_found;
num_found = 0;
node *n = findLeaf(root, key_start, verbose);
if (n == NULL)
return 0;
for (i = 0; i < n->num_keys && n->keys[i] < key_start; i++)
;
if (i == n->num_keys)
return 0;
while (n != NULL) {
for (; i < n->num_keys && n->keys[i] <= key_end; i++) {
returned_keys[num_found] = n->keys[i];
returned_pointers[num_found] = n->pointers[i];
num_found++;
}
n = n->pointers[order - 1];
i = 0;
}
return num_found;
}
// Find the leaf
node *findLeaf(node *const root, int key, bool verbose) {
if (root == NULL) {
if (verbose)
printf("Empty tree.\n");
return root;
}
int i = 0;
node *c = root;
while (!c->is_leaf) {
if (verbose) {
printf("[");
for (i = 0; i < c->num_keys - 1; i++)
printf("%d ", c->keys[i]);
printf("%d] ", c->keys[i]);
}
i = 0;
while (i < c->num_keys) {
if (key >= c->keys[i])
i++;
else
break;
}
if (verbose)
printf("%d ->\n", i);
c = (node *)c->pointers[i];
}
if (verbose) {
printf("Leaf [");
for (i = 0; i < c->num_keys - 1; i++)
printf("%d ", c->keys[i]);
printf("%d] ->\n", c->keys[i]);
}
return c;
}
record *find(node *root, int key, bool verbose, node **leaf_out) {
if (root == NULL) {
if (leaf_out != NULL) {
*leaf_out = NULL;
}
return NULL;
}
int i = 0;
node *leaf = NULL;
leaf = findLeaf(root, key, verbose);
for (i = 0; i < leaf->num_keys; i++)
if (leaf->keys[i] == key)
break;
if (leaf_out != NULL) {
*leaf_out = leaf;
}
if (i == leaf->num_keys)
return NULL;
else
return (record *)leaf->pointers[i];
}
int cut(int length) {
if (length % 2 == 0)
return length / 2;
else
return length / 2 + 1;
}
record *makeRecord(int value) {
record *new_record = (record *)malloc(sizeof(record));
if (new_record == NULL) {
perror("Record creation.");
exit(EXIT_FAILURE);
} else {
new_record->value = value;
}
return new_record;
}
node *makeNode(void) {
node *new_node;
new_node = malloc(sizeof(node));
if (new_node == NULL) {
perror("Node creation.");
exit(EXIT_FAILURE);
}
new_node->keys = malloc((order - 1) * sizeof(int));
if (new_node->keys == NULL) {
perror("New node keys array.");
exit(EXIT_FAILURE);
}
new_node->pointers = malloc(order * sizeof(void *));
if (new_node->pointers == NULL) {
perror("New node pointers array.");
exit(EXIT_FAILURE);
}
new_node->is_leaf = false;
new_node->num_keys = 0;
new_node->parent = NULL;
new_node->next = NULL;
return new_node;
}
node *makeLeaf(void) {
node *leaf = makeNode();
leaf->is_leaf = true;
return leaf;
}
int getLeftIndex(node *parent, node *left) {
int left_index = 0;
while (left_index <= parent->num_keys &&
parent->pointers[left_index] != left)
left_index++;
return left_index;
}
node *insertIntoLeaf(node *leaf, int key, record *pointer) {
int i, insertion_point;
insertion_point = 0;
while (insertion_point < leaf->num_keys && leaf->keys[insertion_point] < key)
insertion_point++;
for (i = leaf->num_keys; i > insertion_point; i--) {
leaf->keys[i] = leaf->keys[i - 1];
leaf->pointers[i] = leaf->pointers[i - 1];
}
leaf->keys[insertion_point] = key;
leaf->pointers[insertion_point] = pointer;
leaf->num_keys++;
return leaf;
}
node *insertIntoLeafAfterSplitting(node *root, node *leaf, int key, record *pointer) {
node *new_leaf;
int *temp_keys;
void **temp_pointers;
int insertion_index, split, new_key, i, j;
new_leaf = makeLeaf();
temp_keys = malloc(order * sizeof(int));
if (temp_keys == NULL) {
perror("Temporary keys array.");
exit(EXIT_FAILURE);
}
temp_pointers = malloc(order * sizeof(void *));
if (temp_pointers == NULL) {
perror("Temporary pointers array.");
exit(EXIT_FAILURE);
}
insertion_index = 0;
while (insertion_index < order - 1 && leaf->keys[insertion_index] < key)
insertion_index++;
for (i = 0, j = 0; i < leaf->num_keys; i++, j++) {
if (j == insertion_index)
j++;
temp_keys[j] = leaf->keys[i];
temp_pointers[j] = leaf->pointers[i];
}
temp_keys[insertion_index] = key;
temp_pointers[insertion_index] = pointer;
leaf->num_keys = 0;
split = cut(order - 1);
for (i = 0; i < split; i++) {
leaf->pointers[i] = temp_pointers[i];
leaf->keys[i] = temp_keys[i];
leaf->num_keys++;
}
for (i = split, j = 0; i < order; i++, j++) {
new_leaf->pointers[j] = temp_pointers[i];
new_leaf->keys[j] = temp_keys[i];
new_leaf->num_keys++;
}
free(temp_pointers);
free(temp_keys);
new_leaf->pointers[order - 1] = leaf->pointers[order - 1];
leaf->pointers[order - 1] = new_leaf;
for (i = leaf->num_keys; i < order - 1; i++)
leaf->pointers[i] = NULL;
for (i = new_leaf->num_keys; i < order - 1; i++)
new_leaf->pointers[i] = NULL;
new_leaf->parent = leaf->parent;
new_key = new_leaf->keys[0];
return insertIntoParent(root, leaf, new_key, new_leaf);
}
node *insertIntoNode(node *root, node *n,
int left_index, int key, node *right) {
int i;
for (i = n->num_keys; i > left_index; i--) {
n->pointers[i + 1] = n->pointers[i];
n->keys[i] = n->keys[i - 1];
}
n->pointers[left_index + 1] = right;
n->keys[left_index] = key;
n->num_keys++;
return root;
}
node *insertIntoNodeAfterSplitting(node *root, node *old_node, int left_index,
int key, node *right) {
int i, j, split, k_prime;
node *new_node, *child;
int *temp_keys;
node **temp_pointers;
temp_pointers = malloc((order + 1) * sizeof(node *));
if (temp_pointers == NULL) {
exit(EXIT_FAILURE);
}
temp_keys = malloc(order * sizeof(int));
if (temp_keys == NULL) {
exit(EXIT_FAILURE);
}
for (i = 0, j = 0; i < old_node->num_keys + 1; i++, j++) {
if (j == left_index + 1)
j++;
temp_pointers[j] = old_node->pointers[i];
}
for (i = 0, j = 0; i < old_node->num_keys; i++, j++) {
if (j == left_index)
j++;
temp_keys[j] = old_node->keys[i];
}
temp_pointers[left_index + 1] = right;
temp_keys[left_index] = key;
split = cut(order);
new_node = makeNode();
old_node->num_keys = 0;
for (i = 0; i < split - 1; i++) {
old_node->pointers[i] = temp_pointers[i];
old_node->keys[i] = temp_keys[i];
old_node->num_keys++;
}
old_node->pointers[i] = temp_pointers[i];
k_prime = temp_keys[split - 1];
for (++i, j = 0; i < order; i++, j++) {
new_node->pointers[j] = temp_pointers[i];
new_node->keys[j] = temp_keys[i];
new_node->num_keys++;
}
new_node->pointers[j] = temp_pointers[i];
free(temp_pointers);
free(temp_keys);
new_node->parent = old_node->parent;
for (i = 0; i <= new_node->num_keys; i++) {
child = new_node->pointers[i];
child->parent = new_node;
}
return insertIntoParent(root, old_node, k_prime, new_node);
}
node *insertIntoParent(node *root, node *left, int key, node *right) {
int left_index;
node *parent;
parent = left->parent;
if (parent == NULL)
return insertIntoNewRoot(left, key, right);
left_index = getLeftIndex(parent, left);
if (parent->num_keys < order - 1)
return insertIntoNode(root, parent, left_index, key, right);
return insertIntoNodeAfterSplitting(root, parent, left_index, key, right);
}
node *insertIntoNewRoot(node *left, int key, node *right) {
node *root = makeNode();
root->keys[0] = key;
root->pointers[0] = left;
root->pointers[1] = right;
root->num_keys++;
root->parent = NULL;
left->parent = root;
right->parent = root;
return root;
}
node *startNewTree(int key, record *pointer) {
node *root = makeLeaf();
root->keys[0] = key;
root->pointers[0] = pointer;
root->pointers[order - 1] = NULL;
root->parent = NULL;
root->num_keys++;
return root;
}
node *insert(node *root, int key, int value) {
record *record_pointer = NULL;
node *leaf = NULL;
record_pointer = find(root, key, false, NULL);
if (record_pointer != NULL) {
record_pointer->value = value;
return root;
}
record_pointer = makeRecord(value);
if (root == NULL)
return startNewTree(key, record_pointer);
leaf = findLeaf(root, key, false);
if (leaf->num_keys < order - 1) {
leaf = insertIntoLeaf(leaf, key, record_pointer);
return root;
}
return insertIntoLeafAfterSplitting(root, leaf, key, record_pointer);
}
int main() {
node *root;
char instruction;
root = NULL;
root = insert(root, 5, 33);
root = insert(root, 15, 21);
root = insert(root, 25, 31);
root = insert(root, 35, 41);
root = insert(root, 45, 10);
printTree(root);
findAndPrint(root, 15, instruction = 'a');
}in cpp
// Searching on a B+ tree in C++
#include <climits>
#include <fstream>
#include <iostream>
#include <sstream>
using namespace std;
int MAX = 3;
// BP node
class Node {
bool IS_LEAF;
int *key, size;
Node **ptr;
friend class BPTree;
public:
Node();
};
// BP tree
class BPTree {
Node *root;
void insertInternal(int, Node *, Node *);
Node *findParent(Node *, Node *);
public:
BPTree();
void search(int);
void insert(int);
void display(Node *);
Node *getRoot();
};
Node::Node() {
key = new int[MAX];
ptr = new Node *[MAX + 1];
}
BPTree::BPTree() {
root = NULL;
}
// Search operation
void BPTree::search(int x) {
if (root == NULL) {
cout << "Tree is empty\n";
} else {
Node *cursor = root;
while (cursor->IS_LEAF == false) {
for (int i = 0; i < cursor->size; i++) {
if (x < cursor->key[i]) {
cursor = cursor->ptr[i];
break;
}
if (i == cursor->size - 1) {
cursor = cursor->ptr[i + 1];
break;
}
}
}
for (int i = 0; i < cursor->size; i++) {
if (cursor->key[i] == x) {
cout << "Found\n";
return;
}
}
cout << "Not found\n";
}
}
// Insert Operation
void BPTree::insert(int x) {
if (root == NULL) {
root = new Node;
root->key[0] = x;
root->IS_LEAF = true;
root->size = 1;
} else {
Node *cursor = root;
Node *parent;
while (cursor->IS_LEAF == false) {
parent = cursor;
for (int i = 0; i < cursor->size; i++) {
if (x < cursor->key[i]) {
cursor = cursor->ptr[i];
break;
}
if (i == cursor->size - 1) {
cursor = cursor->ptr[i + 1];
break;
}
}
}
if (cursor->size < MAX) {
int i = 0;
while (x > cursor->key[i] && i < cursor->size)
i++;
for (int j = cursor->size; j > i; j--) {
cursor->key[j] = cursor->key[j - 1];
}
cursor->key[i] = x;
cursor->size++;
cursor->ptr[cursor->size] = cursor->ptr[cursor->size - 1];
cursor->ptr[cursor->size - 1] = NULL;
} else {
Node *newLeaf = new Node;
int virtualNode[MAX + 1];
for (int i = 0; i < MAX; i++) {
virtualNode[i] = cursor->key[i];
}
int i = 0, j;
while (x > virtualNode[i] && i < MAX)
i++;
for (int j = MAX + 1; j > i; j--) {
virtualNode[j] = virtualNode[j - 1];
}
virtualNode[i] = x;
newLeaf->IS_LEAF = true;
cursor->size = (MAX + 1) / 2;
newLeaf->size = MAX + 1 - (MAX + 1) / 2;
cursor->ptr[cursor->size] = newLeaf;
newLeaf->ptr[newLeaf->size] = cursor->ptr[MAX];
cursor->ptr[MAX] = NULL;
for (i = 0; i < cursor->size; i++) {
cursor->key[i] = virtualNode[i];
}
for (i = 0, j = cursor->size; i < newLeaf->size; i++, j++) {
newLeaf->key[i] = virtualNode[j];
}
if (cursor == root) {
Node *newRoot = new Node;
newRoot->key[0] = newLeaf->key[0];
newRoot->ptr[0] = cursor;
newRoot->ptr[1] = newLeaf;
newRoot->IS_LEAF = false;
newRoot->size = 1;
root = newRoot;
} else {
insertInternal(newLeaf->key[0], parent, newLeaf);
}
}
}
}
// Insert Operation
void BPTree::insertInternal(int x, Node *cursor, Node *child) {
if (cursor->size < MAX) {
int i = 0;
while (x > cursor->key[i] && i < cursor->size)
i++;
for (int j = cursor->size; j > i; j--) {
cursor->key[j] = cursor->key[j - 1];
}
for (int j = cursor->size + 1; j > i + 1; j--) {
cursor->ptr[j] = cursor->ptr[j - 1];
}
cursor->key[i] = x;
cursor->size++;
cursor->ptr[i + 1] = child;
} else {
Node *newInternal = new Node;
int virtualKey[MAX + 1];
Node *virtualPtr[MAX + 2];
for (int i = 0; i < MAX; i++) {
virtualKey[i] = cursor->key[i];
}
for (int i = 0; i < MAX + 1; i++) {
virtualPtr[i] = cursor->ptr[i];
}
int i = 0, j;
while (x > virtualKey[i] && i < MAX)
i++;
for (int j = MAX + 1; j > i; j--) {
virtualKey[j] = virtualKey[j - 1];
}
virtualKey[i] = x;
for (int j = MAX + 2; j > i + 1; j--) {
virtualPtr[j] = virtualPtr[j - 1];
}
virtualPtr[i + 1] = child;
newInternal->IS_LEAF = false;
cursor->size = (MAX + 1) / 2;
newInternal->size = MAX - (MAX + 1) / 2;
for (i = 0, j = cursor->size + 1; i < newInternal->size; i++, j++) {
newInternal->key[i] = virtualKey[j];
}
for (i = 0, j = cursor->size + 1; i < newInternal->size + 1; i++, j++) {
newInternal->ptr[i] = virtualPtr[j];
}
if (cursor == root) {
Node *newRoot = new Node;
newRoot->key[0] = cursor->key[cursor->size];
newRoot->ptr[0] = cursor;
newRoot->ptr[1] = newInternal;
newRoot->IS_LEAF = false;
newRoot->size = 1;
root = newRoot;
} else {
insertInternal(cursor->key[cursor->size], findParent(root, cursor), newInternal);
}
}
}
// Find the parent
Node *BPTree::findParent(Node *cursor, Node *child) {
Node *parent;
if (cursor->IS_LEAF || (cursor->ptr[0])->IS_LEAF) {
return NULL;
}
for (int i = 0; i < cursor->size + 1; i++) {
if (cursor->ptr[i] == child) {
parent = cursor;
return parent;
} else {
parent = findParent(cursor->ptr[i], child);
if (parent != NULL)
return parent;
}
}
return parent;
}
// Print the tree
void BPTree::display(Node *cursor) {
if (cursor != NULL) {
for (int i = 0; i < cursor->size; i++) {
cout << cursor->key[i] << " ";
}
cout << "\n";
if (cursor->IS_LEAF != true) {
for (int i = 0; i < cursor->size + 1; i++) {
display(cursor->ptr[i]);
}
}
}
}
// Get the root
Node *BPTree::getRoot() {
return root;
}
int main() {
BPTree node;
node.insert(5);
node.insert(15);
node.insert(25);
node.insert(35);
node.insert(45);
node.insert(55);
node.insert(40);
node.insert(30);
node.insert(20);
node.display(node.getRoot());
node.search(15);
}Search Complexity
Time Complexity
If linear search is implemented inside a node, then total complexity is Θ(logt n).
If binary search is used, then total complexity is Θ(log2t.logt n).
Insertion
Inserting an element into a B+ tree consists of three main events: searching the appropriate leaf, inserting the element and balancing/splitting the tree.
Let us understand these events below.
Insertion Operation
Before inserting an element into a B+ tree, these properties must be kept in mind.
- The root has at least two children.
- Each node except root can have a maximum of
mchildren and at leastm/2children. - Each node can contain a maximum of
m - 1keys and a minimum of⌈m/2⌉ - 1keys.
The following steps are followed for inserting an element.
- Since every element is inserted into the leaf node, go to the appropriate leaf node.
- Insert the key into the leaf node.
Case I
- If the leaf is not full, insert the key into the leaf node in increasing order.
Case II
- If the leaf is full, insert the key into the leaf node in increasing order and balance the tree in the following way.
- Break the node at m/2th position.
- Add m/2th key to the parent node as well.
- If the parent node is already full, follow steps 2 to 3.
Example
Let us understand the insertion operation with the illustrations below.
The elements to be inserted are 5,15, 25, 35, 45.
-
Insert 5.

-
Insert 15.

-
Insert 25.
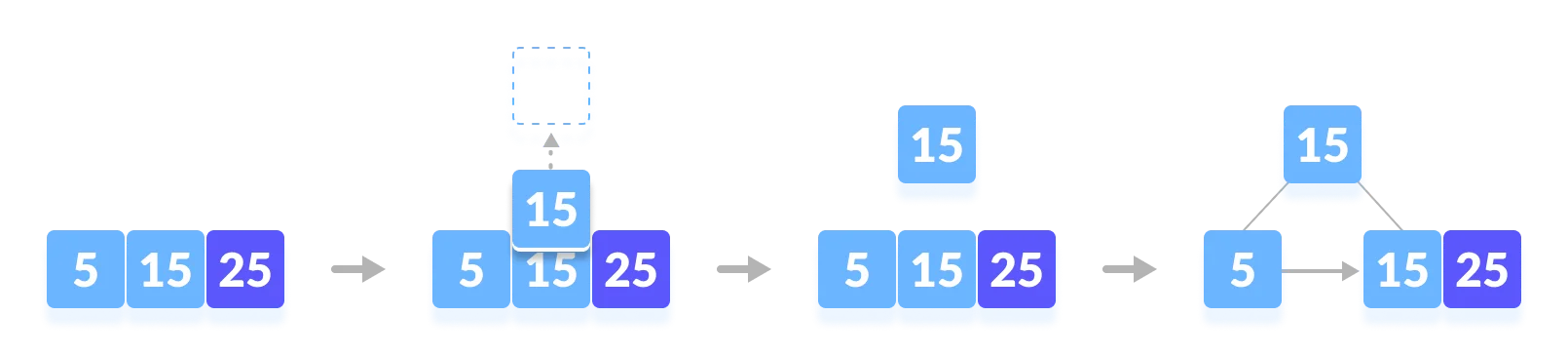
-
Insert 35.
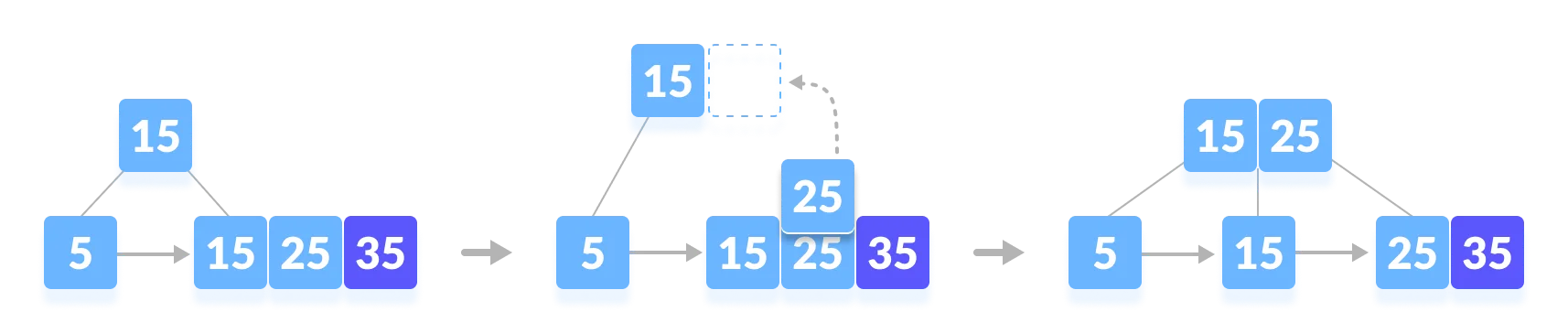
-
Insert 45.
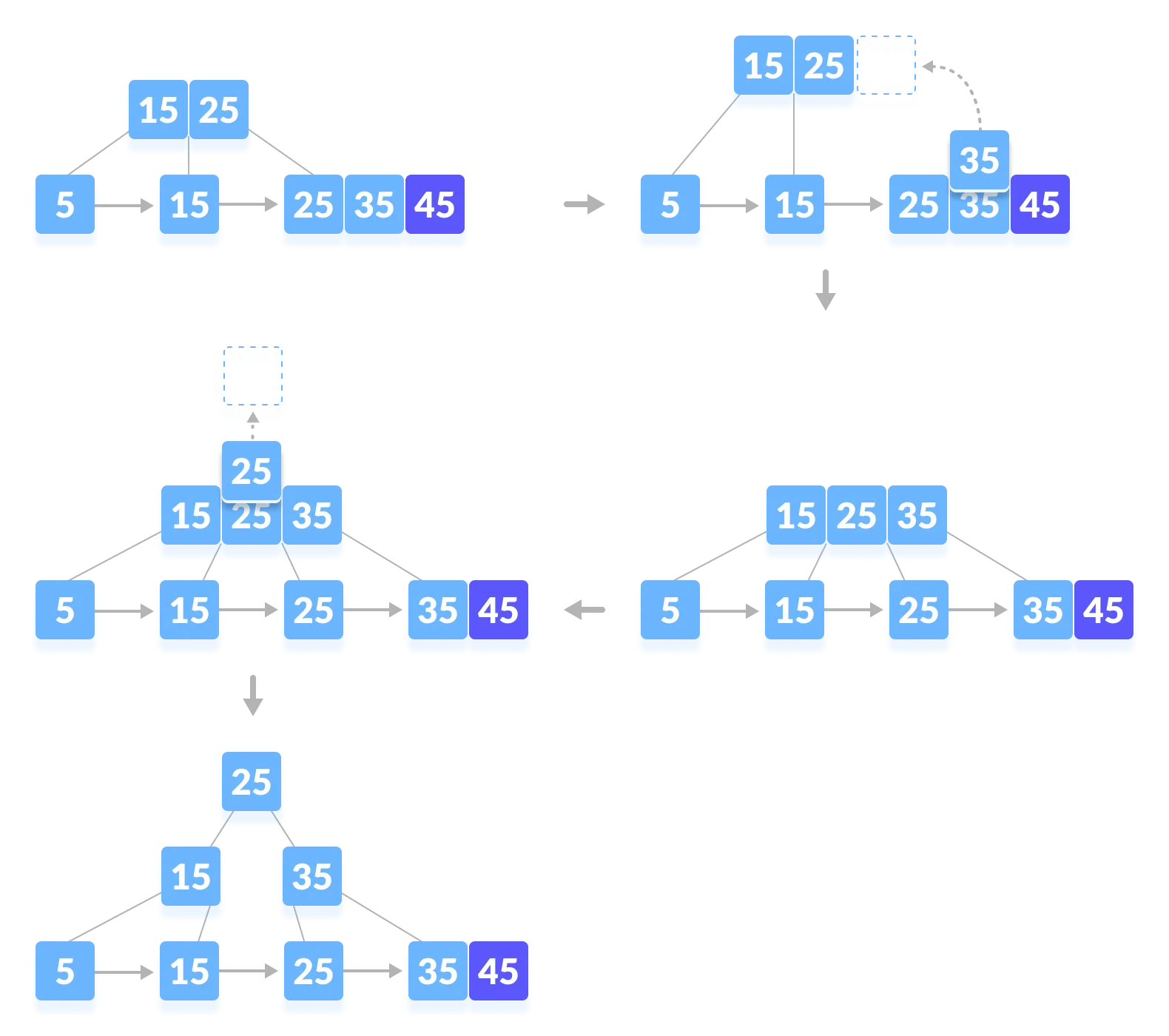
Insertion Complexity
-
Time complexity:
-
The complexity is dominated by .
Delete
Deleting an element on a B+ tree consists of three main events: searching the node where the key to be deleted exists, deleting the key and balancing the tree if required.Underflow is a situation when there is less number of keys in a node than the minimum number of keys it should hold.
Deletion Operation
Before going through the steps below, one must know these facts about a B+ tree of degree m.
- A node can have a maximum of m children. (i.e. 3)
- A node can contain a maximum of
m - 1keys. (i.e. 2) - A node should have a minimum of
⌈m/2⌉children. (i.e. 2) - A node (except root node) should contain a minimum of
⌈m/2⌉ - 1keys. (i.e. 1)
While deleting a key, we have to take care of the keys present in the internal nodes (i.e. indexes) as well because the values are redundant in a B+ tree. Search the key to be deleted then follow the following steps.
Case I
The key to be deleted is present only at the leaf node not in the indexes (or internal nodes). There are two cases for it:
-
There is more than the minimum number of keys in the node. Simply delete the key.
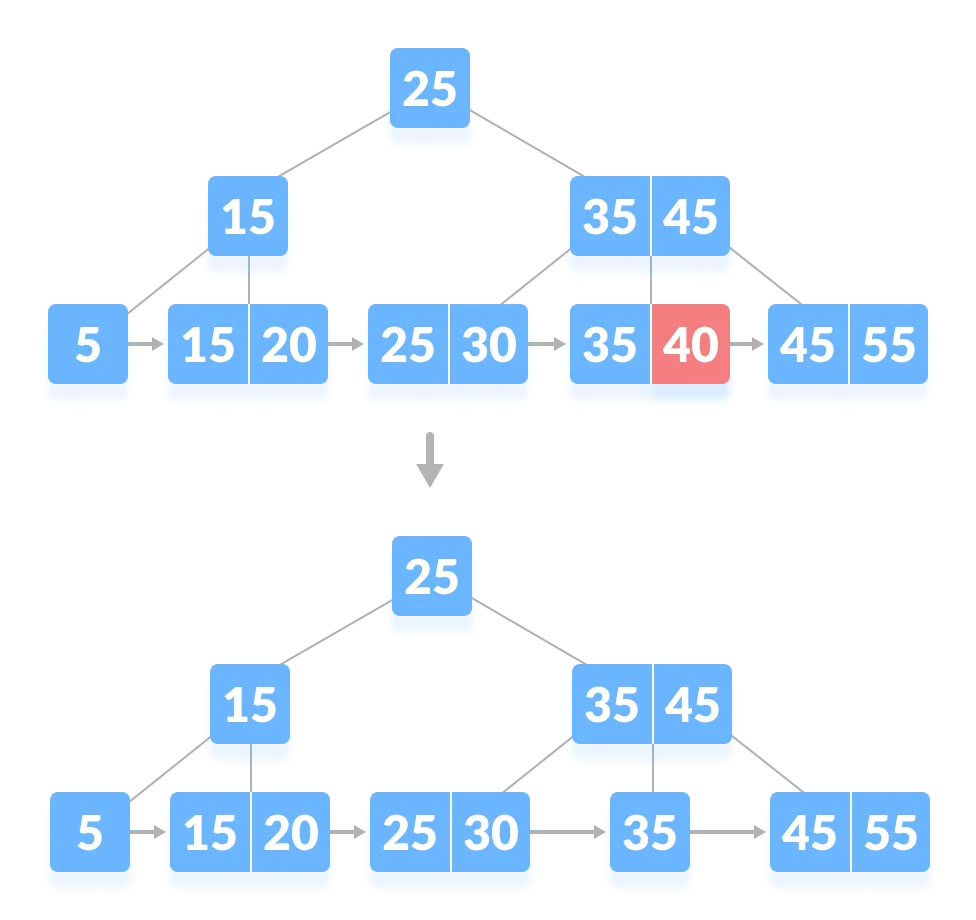
-
There is an exact minimum number of keys in the node. Delete the key and borrow a key from the immediate sibling. Add the median key of the sibling node to the parent.
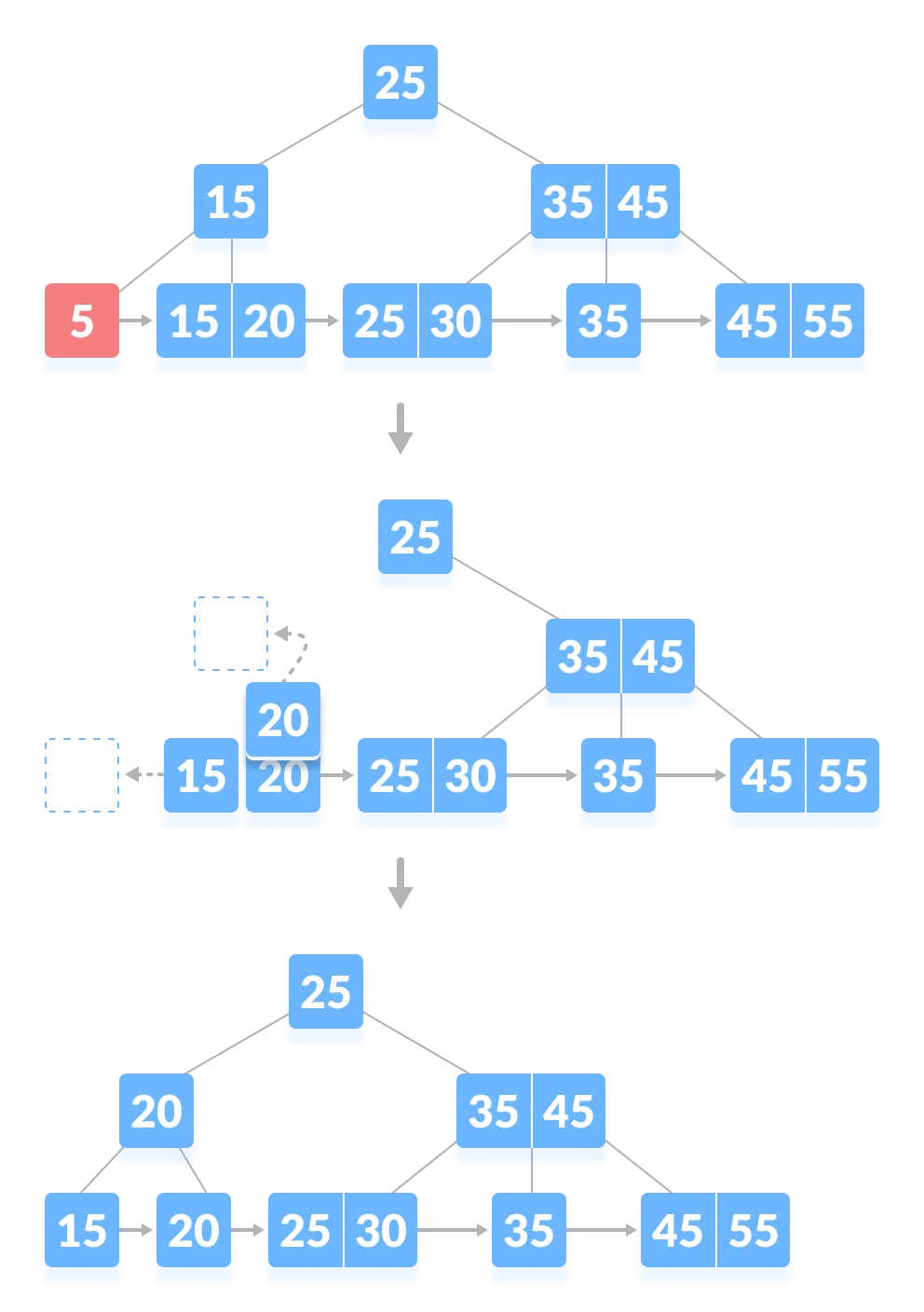
Case II
The key to be deleted is present in the internal nodes as well. Then we have to remove them from the internal nodes as well. There are the following cases for this situation.
-
If there is more than the minimum number of keys in the node, simply delete the key from the leaf node and delete the key from the internal node as well. Fill the empty space in the internal node with the inorder successor.
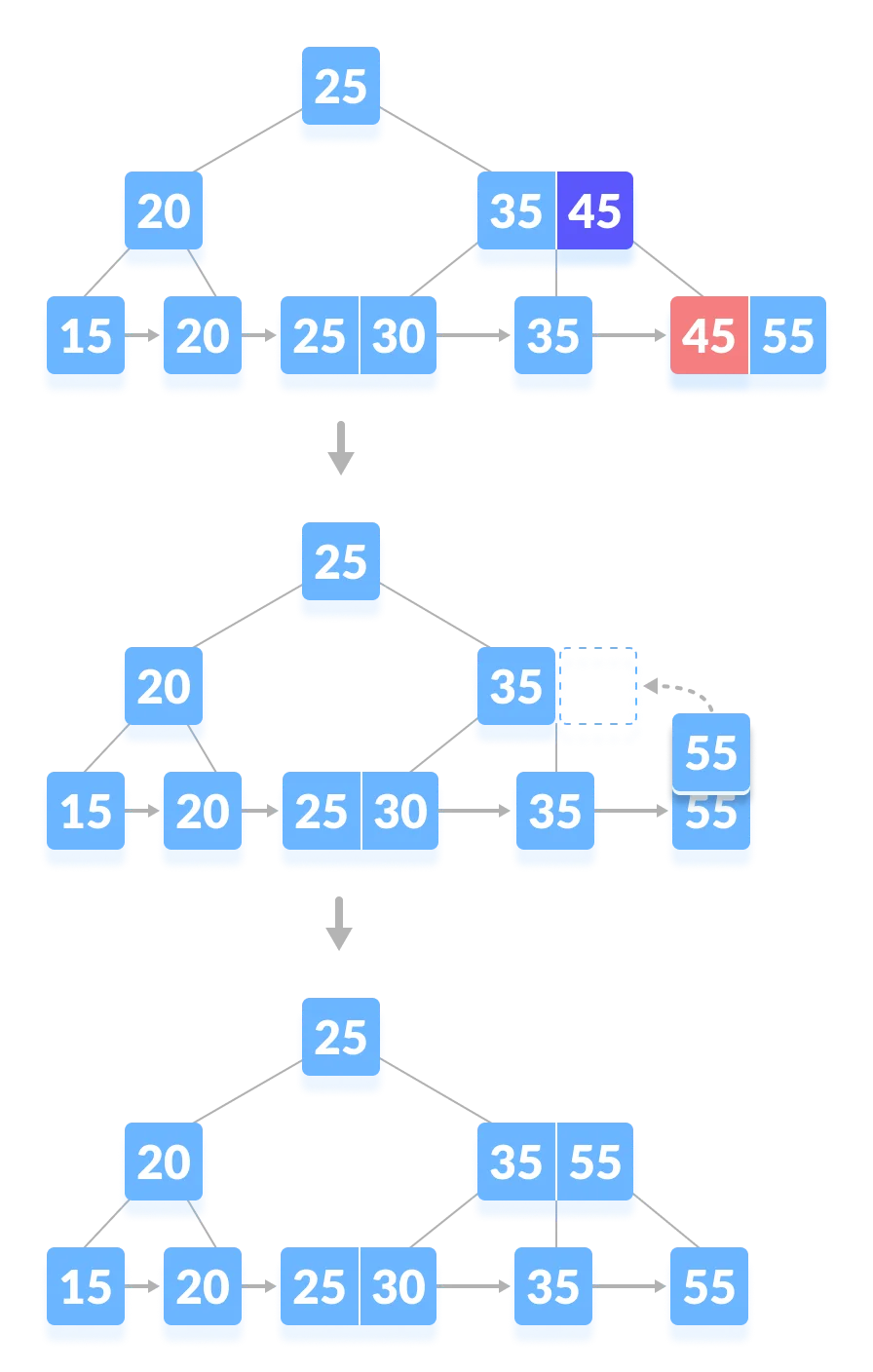
-
If there is an exact minimum number of keys in the node, then delete the key and borrow a key from its immediate sibling (through the parent). Fill the empty space created in the index (internal node) with the borrowed key.
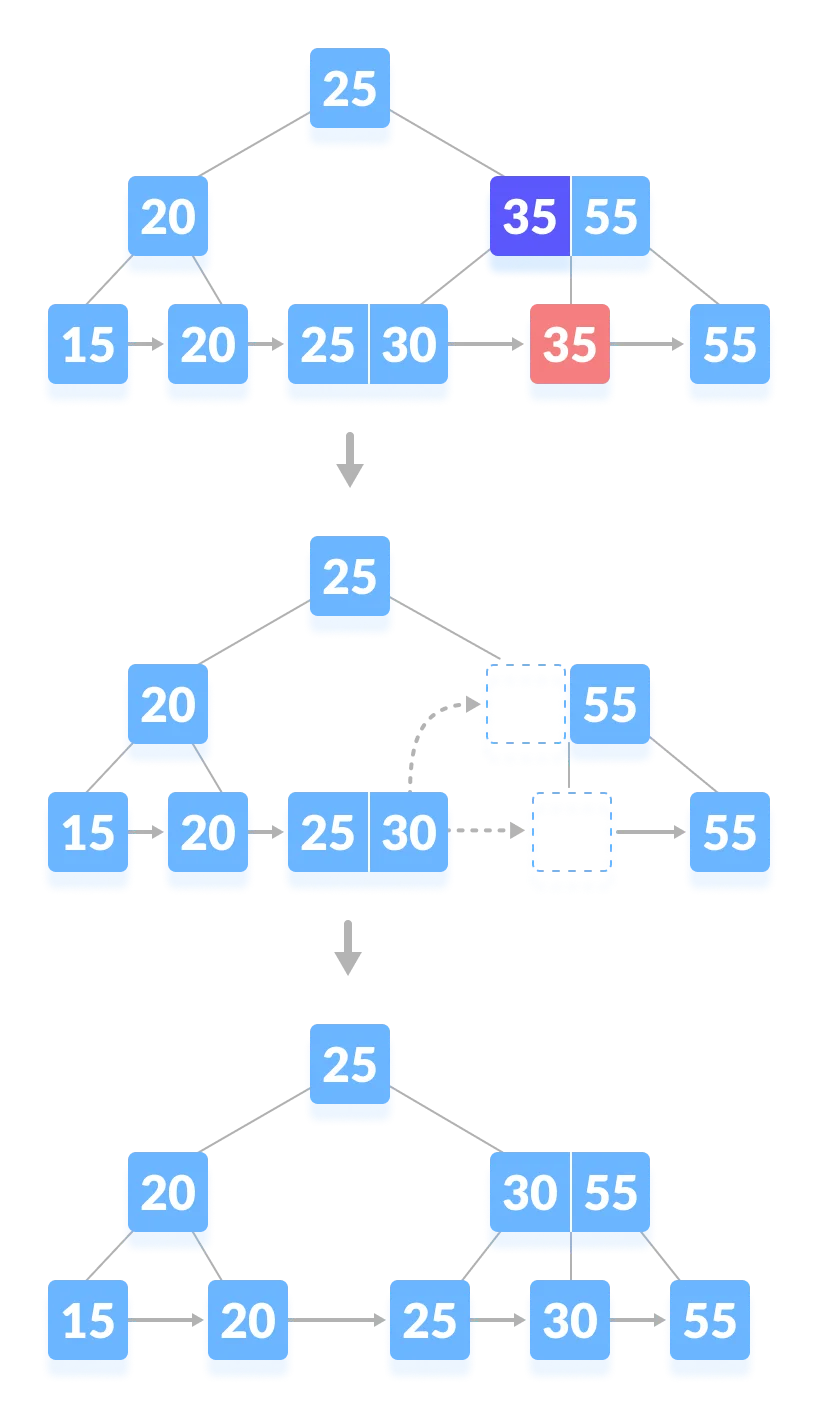
-
This case is similar to Case II (1) but here, empty space is generated above the immediate parent node. After deleting the key, merge the empty space with its sibling. Fill the empty space in the grandparent node with the inorder successor.
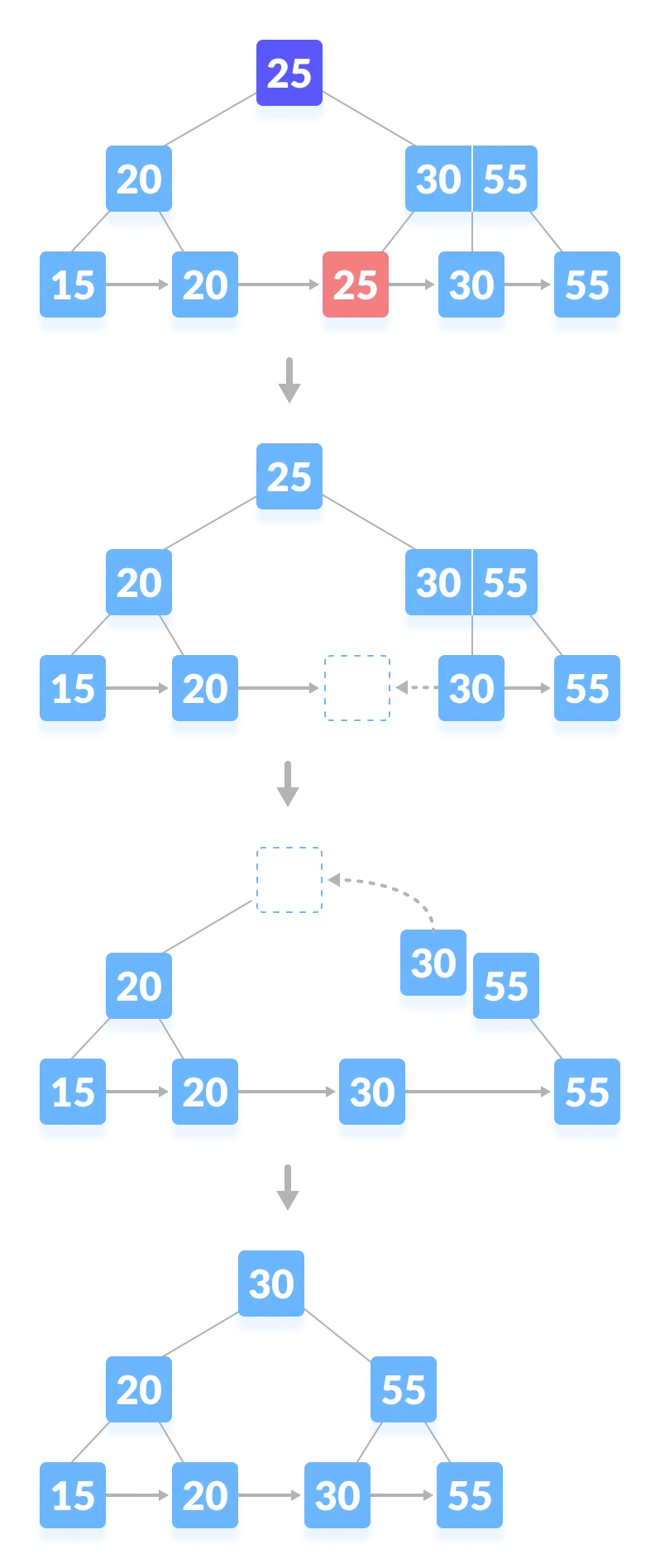
Case III
In this case, the height of the tree gets shrinked. It is a little complicated.Deleting 55 from the tree below leads to this condition. It can be understood in the illustrations below.