95-Skew-heap

Introduction

[! warning] Not to be confused with Skew binomial heap.

A skew heap (or self-adjusting heap) is a heap data structure implemented as a binary tree. Skew heaps are advantageous because of their ability to merge more quickly than binary heaps. In contrast with binary heaps, there are no structural constraints, so there is no guarantee that the height of the tree is logarithmic. Only two conditions must be satisfied:

The general heap order must be enforced
Every operation (add, remove_min, merge) on two skew heaps must be done using a special skew heap merge.

A skew heap is a self-adjusting form of a leftist heap which attempts to maintain balance by unconditionally swapping all nodes in the merge path when merging two heaps. (The merge operation is also used when adding and removing values.) With no structural constraints, it may seem that a skew heap would be horribly inefficient. However, amortized complexity analysis can be used to demonstrate that all operations on a skew heap can be done in O(logn)¹. In fact, with $φ = \frac{1 + 5}{2}$ denoting the golden ratio, the exact amortized complexity is known to be $lo g_{φ} n$ (approximately $1.44 lo g_{2} n$ ).²,³

Definition

Skew heaps may be described with the following recursive definition:

A heap with only one element is a skew heap.
The result of skew merging two skew heaps $s h_{1}$ and $s h_{2}$ is also a skew heap.

Features

Only two conditions must be satisfied :

The general heap order must be there (root is minimum and same is recursively true for subtrees), but balanced property (all levels must be full except the last) is not required.

一般堆序必须存在（根最小，子树也递归为真），但不需要平衡属性（除最后一级外，所有级别都必须满）。

Main operation in Skew Heaps is Merge. We can implement other operations like insert, extractMin (), etc using Merge only.

Recursive Merge Process :
merge (h1, h2)

Let h1 and h2 be the two min skew heaps to be merged. Let h1’s root be smaller than h2’s root (If not smaller, we can swap to get the same).
We swap h1→left and h1→right.
h1→left = merge (h2, h1→left)

Examples :

Let h1 be
        10
     /    \
   20      30
  /        /
40        50

Let h2 be
       15
     /    \
   25      35
  /  \
45    55

After swapping h1->left and h1->right, we get
        10
     /    \
   30      20
  /        /
50        40

Now we recursively Merge
   30
   /     AND   
  50

       15
     /    \
   25      35
  /  \
45    55
After recursive merge, we get (Please do it 
using pen and paper).
        15
     /     \
   30        25
  /  \     /    \
35    50  45    55

We make this merged tree as left of original
h1 and we get following result.
             10
         /         \
       15           20
    /      \       /   
   30       25    40   
 /   \    /    \
35   40  45    55

For visualization : https://www.cs.usfca.edu/~galles/JavascriptVisual/LeftistHeap.html

Operations

Merging two heaps

When two skew heaps are to be merged, we can use a similar process as the merge of two leftist heaps:

Compare roots of two heaps; let p be the heap with the smaller root, and q be the other heap. Let r be the name of the resulting new heap.
Let the root of r be the root of p (the smaller root), and let r’s right subtree be p’s left subtree.
Now, compute r’s left subtree by recursively merging p’s right subtree with q.

template<class T, class CompareFunction>
SkewNode<T>* CSkewHeap<T, CompareFunction>::Merge(SkewNode<T>* root_1, SkewNode<T>* root_2)
{
    SkewNode<T>* firstRoot = root_1;
    SkewNode<T>* secondRoot = root_2;

    if (firstRoot == NULL)
        return secondRoot;

    else if (secondRoot == NULL)
        return firstRoot;

    if (sh_compare->Less(firstRoot->key, secondRoot->key))
    {
        SkewNode<T>* tempHeap = firstRoot->rightNode;
        firstRoot->rightNode = firstRoot->leftNode;
        firstRoot->leftNode = Merge(secondRoot, tempHeap);
        return firstRoot;
    }
    else
        return Merge(secondRoot, firstRoot);
}

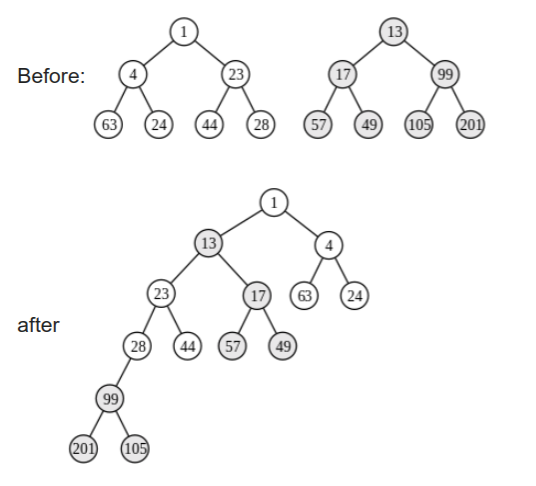
Non-recursive merging

Alternatively, there is a non-recursive approach which is more wordy, and does require some sorting at the outset.

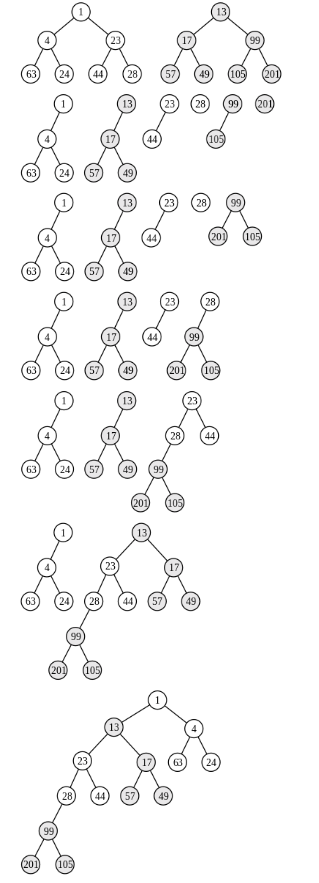
Split each heap into subtrees by cutting every path. (From the root node, sever the right node and make the right child its own subtree.) This will result in a set of trees in which the root either only has a left child or no children at all.
Sort the subtrees in ascending order based on the value of the root node of each subtree.
While there are still multiple subtrees, iteratively recombine the last two (from right to left).
- If the root of the second-to-last subtree has a left child, swap it to be the right child.
- Link the root of the last subtree as the left child of the second-to-last subtree.

Insert values

Adding a value to a skew heap is like merging a tree with one node together with the original tree.

Remove values

Removing the first value in a heap can be accomplished by removing the root and merging its child subtrees.

Implementation

CPP

// CPP program to implement Skew Heap
// operations.
#include <bits/stdc++.h>
using namespace std;
 
struct SkewHeap
{
	int key;
	SkewHeap* right;
	SkewHeap* left;
 
	// constructor to make a new
	// node of heap
	SkewHeap()
	{
		key = 0;
		right = NULL;
		left = NULL;
	}
 
	// the special merge function that's
	// used in most of the other operations
	// also
	SkewHeap* merge(SkewHeap* h1, SkewHeap* h2)
	{
		// If one of the heaps is empty
		if (h1 == NULL)
			return h2;
		if (h2 == NULL)
			return h1;
 
		// Make sure that h1 has smaller
		// key.
		if (h1->key > h2->key)
		swap(h1, h2);
 
		// Swap h1->left and h1->right
		swap(h1->left, h1->right);
 
		// Merge h2 and h1->left and make
		// merged tree as left of h1.
		h1->left = merge(h2, h1->left);
 
		return h1;
	}
 
	// function to construct heap using
	// values in the array
	SkewHeap* construct(SkewHeap* root,
					int heap[], int n)
	{
		SkewHeap* temp;
		for (int i = 0; i < n; i++) {
			temp = new SkewHeap;
			temp->key = heap[i];
			root = merge(root, temp);
		}
		return root;
	}
 
	// function to print the Skew Heap,
	// as it is in form of a tree so we use
	// tree traversal algorithms
	void inorder(SkewHeap* root)
	{
		if (root == NULL)
			return;
		else {
			inorder(root->left);
			cout << root->key << " ";
			inorder(root->right);
		}
		return;
	}
};
 
// Driver Code
int main()
{
	// Construct two heaps
	SkewHeap heap, *temp1 = NULL,
				*temp2 = NULL;
	/*
			5
		/ \
		/ \
		10 12 */
	int heap1[] = { 12, 5, 10 };
	/*
			3
		/ \
		/ \
		7	 8
		/
	/
	14 */
	int heap2[] = { 3, 7, 8, 14 };
	int n1 = sizeof(heap1) / sizeof(heap1[0]);
	int n2 = sizeof(heap2) / sizeof(heap2[0]);
	temp1 = heap.construct(temp1, heap1, n1);
	temp2 = heap.construct(temp2, heap2, n2);
 
	// Merge two heaps
	temp1 = heap.merge(temp1, temp2);
	/*
			3
		/ \
		/ \
		5	 7
		/ \ /
	8 10 14
	/
	12 */
	cout << "Merged Heap is: " << endl;
	heap.inorder(temp1);
}

Java

// Java program to implement Skew Heap operations.
import java.util.*;
 
class SkewHeap {
	int key;
	SkewHeap right;
	SkewHeap left;
 
	// constructor to make a new
	// node of heap
	SkewHeap()
	{
		key = 0;
		right = null;
		left = null;
	}
 
	// the special merge function that's
	// used in most of the other operations
	// also
	SkewHeap merge(SkewHeap h1, SkewHeap h2)
	{
		// If one of the heaps is empty
		if (h1 == null)
			return h2;
		if (h2 == null)
			return h1;
 
		// Make sure that h1 has smaller
		// key.
		if (h1.key > h2.key) {
			SkewHeap temp = h1;
			h1 = h2;
			h2 = temp;
		}
 
		// Swap h1.left and h1.right
		SkewHeap temp = h1.left;
		h1.left = h1.right;
		h1.right = temp;
 
		// Merge h2 and h1.left and make
		// merged tree as left of h1.
		h1.left = merge(h2, h1.left);
 
		return h1;
	}
 
	// function to construct heap using
	// values in the array
	SkewHeap construct(SkewHeap root, int[] heap, int n)
	{
		SkewHeap temp;
		for (int i = 0; i < n; i++) {
			temp = new SkewHeap();
			temp.key = heap[i];
			root = merge(root, temp);
		}
		return root;
	}
 
	// function to print the Skew Heap,
	// as it is in form of a tree so we use
	// tree traversal algorithms
	void inorder(SkewHeap root)
	{
		if (root == null)
			return;
		else {
			inorder(root.left);
			System.out.print(root.key + " ");
			inorder(root.right);
		}
		return;
	}
}
 
// Driver Code
public class Main {
	public static void main(String[] args)
	{
		// Construct two heaps
		SkewHeap heap = new SkewHeap(), temp1 = null,
				temp2 = null;
		/*
		5
		/
		/
		10 12 /
		
		/
		3
		/
		/
		7 8
		/
		/
		14 */
	int[] heap1 = { 12, 5, 10 };
		int[] heap2 = { 3, 7, 8, 14 };
		int n1 = heap1.length;
		int n2 = heap2.length;
		temp1 = heap.construct(temp1, heap1, n1);
		temp2 = heap.construct(temp2, heap2, n2);
 
		// Merge two heaps
		temp1 = heap.merge(temp1, temp2);
		/*
			3
		/ \
		/ \
		5	 7
		/ \ /
	8 10 14
	/
	12 */
		System.out.println("Merged Heap is: ");
		heap.inorder(temp1);
	}
}

Python3

# Python code implementation

class SkewHeap:
	def __init__(self):
		self.key = 0
		self.right = None
		self.left = None

	# the special merge function that's used 
	# in most of the other operations also
	def merge(self, h1, h2):
		# If one of the heaps is empty
		if h1 is None:
			return h2
		if h2 is None:
			return h1

		# Make sure that h1 has smaller key.
		if h1.key > h2.key:
			h1, h2 = h2, h1

		# Swap h1.left and h1.right
		h1.left, h1.right = h1.right, h1.left

		# Merge h2 and h1.left and make 
		# merged tree as left of h1.
		h1.left = self.merge(h2, h1.left)

		return h1

	# function to construct heap using values in the array
	def construct(self, root, heap, n):
		for i in range(n):
			temp = SkewHeap()
			temp.key = heap[i]
			root = self.merge(root, temp)
		return root

	# function to print the Skew Heap, as it is 
	# in form of a tree so we use
	# tree traversal algorithms
	def inorder(self, root):
		if root is None:
			return
		else:
			self.inorder(root.left)
			print(root.key, end=" ")
			self.inorder(root.right)

# Driver Code
if __name__ == "__main__":
	# Construct two heaps
	heap, temp1, temp2 = SkewHeap(), None, None
	heap1 = [12, 5, 10]
	heap2 = [3, 7, 8, 14]
	n1 = len(heap1)
	n2 = len(heap2)
	temp1 = heap.construct(temp1, heap1, n1)
	temp2 = heap.construct(temp2, heap2, n2)

	# Merge two heaps
	temp1 = heap.merge(temp1, temp2)

	print("The heap obtained after merging is:")
	heap.inorder(temp1)

# This code is contributed by karthik.

C#

using System;

class SkewHeap {
	int key;
	SkewHeap right;
	SkewHeap left;

	// constructor to make a new
	// node of heap
	public SkewHeap()
	{
		key = 0;
		right = null;
		left = null;
	}

	// the special merge function that's
	// used in most of the other operations
	// also
	public SkewHeap merge(SkewHeap h1, SkewHeap h2)
	{
		// If one of the heaps is empty
		if (h1 == null)
			return h2;
		if (h2 == null)
			return h1;

		// Make sure that h1 has smaller
		// key.
		if (h1.key > h2.key) {
			SkewHeap temp = h1;
			h1 = h2;
			h2 = temp;
		}

		// Swap h1.left and h1.right
		SkewHeap temp2 = h1.left;
		h1.left = h1.right;
		h1.right = temp2;

		// Merge h2 and h1.left and make
		// merged tree as left of h1.
		h1.left = merge(h2, h1.left);

		return h1;
	}

	// function to construct heap using
	// values in the array
	public SkewHeap construct(SkewHeap root, int[] heap,
							int n)
	{
		SkewHeap temp;
		for (int i = 0; i < n; i++) {
			temp = new SkewHeap();
			temp.key = heap[i];
			root = merge(root, temp);
		}
		return root;
	}

	// function to print the Skew Heap,
	// as it is in form of a tree so we use
	// tree traversal algorithms
	public void inorder(SkewHeap root)
	{
		if (root == null)
			return;
		else {
			inorder(root.left);
			Console.Write(root.key + " ");
			inorder(root.right);
		}
		return;
	}
}

// Driver Code
class Program {
	static void Main(string[] args)
	{
		// Construct two heaps
		SkewHeap heap = new SkewHeap(), temp1 = null,
				temp2 = null;
		/*
		5
		/
		/
		10 12 /


			/
			3
			/
			/
			7 8
			/
			/
			14 */
		int[] heap1 = { 12, 5, 10 };
		int[] heap2 = { 3, 7, 8, 14 };
		int n1 = heap1.Length;
		int n2 = heap2.Length;
		temp1 = heap.construct(temp1, heap1, n1);
		temp2 = heap.construct(temp2, heap2, n2);

		// Merge two heaps
		temp1 = heap.merge(temp1, temp2);
		/*
			3
			/ \
		/ \
		5	 7
		/ \ /
	8 10 14
	/
	12 */
		Console.WriteLine("Merged Heap is: ");
		heap.inorder(temp1);
	}
}

Javascript

// JavaScript code implementation
class SkewHeap {
constructor() {
	this.key = 0;
	this.right = null;
	this.left = null;
}

// the special merge function that's
// used in most of the other operations
// also
merge(h1, h2) {
	// If one of the heaps is empty
	if (h1 == null) return h2;
	if (h2 == null) return h1;

	// Make sure that h1 has smaller key.
	if (h1.key > h2.key) {
	[h1, h2] = [h2, h1];
	}

	// Swap h1.left and h1.right
	[h1.left, h1.right] = [h1.right, h1.left];

	// Merge h2 and h1.left and make merged tree as left of h1.
	h1.left = this.merge(h2, h1.left);

	return h1;
}

// function to construct heap using values in the array
construct(root, heap, n) {
	let temp;
	for (let i = 0; i < n; i++) {
	temp = new SkewHeap();
	temp.key = heap[i];
	root = this.merge(root, temp);
	}
	return root;
}

// function to print the Skew Heap,
// as it is in form of a tree so we use
// tree traversal algorithms
inorder(root) {
	if (root == null) return;
	else {
	this.inorder(root.left);
	console.log(root.key + " ");
	this.inorder(root.right);
	}
	return;
}
}

// Driver Code
// Construct two heaps
let heap = new SkewHeap(),
temp1 = null,
temp2 = null;

let heap1 = [12, 5, 10];
let heap2 = [3, 7, 8, 14];
let n1 = heap1.length;
let n2 = heap2.length;
temp1 = heap.construct(temp1, heap1, n1);
temp2 = heap.construct(temp2, heap2, n2);

// Merge two heaps
temp1 = heap.merge(temp1, temp2);

console.log("The heap obtained after merging is: <br>");
heap.inorder(temp1);

// This code is contributed by sankar.

Output

The heap obtained after merging is: 
12  8  5  10  3  14  7

Analysis

Time Complexity: O(NlogN)

Auxiliary Space: O(N)

Sleator, Daniel Dominic; Tarjan, Robert Endre (February 1986). “Self-Adjusting Heaps”. _SIAM Journal on Computing _. 15 (1): 52–69. CiteSeerX 10.1.1.93.6678. doi: 10.1137/0215004. ↩
Kaldewaij, Anne; Schoenmakers, Berry (1991). “The Derivation of a Tighter Bound for Top-Down Skew Heaps” . Information Processing Letters. 37 (5): 265–271. CiteSeerX 10.1.1.56.8717. doi:10.1016/0020-0190(91)90218-7. ↩
Schoenmakers, Berry (1997). “A Tight Lower Bound for Top-Down Skew Heaps”. Information Processing Letters. 61 (5): 279–284. CiteSeerX 10.1.1.47.447. doi: 10.1016/S0020-0190(97)00028-8. S2CID 11288837. ↩

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索

95-Skew-heap

Introduction

Definition

Features

Operations

Merging two heaps

Non-recursive merging

Insert values

Remove values

Implementation

CPP

Java

Python3

C#

Javascript

Output

Analysis

关系图谱

目录

反向链接

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索

95-Skew-heap

Introduction

Definition

Features

Operations

Merging two heaps

Non-recursive merging

Insert values

Remove values

Implementation

CPP

Java

Python3

C#

Javascript

Output

Analysis

Footnotes

关系图谱

目录

反向链接