70-Blending-and-Bagging

Motivation of Aggregation

如果已经预先知晓数据集的一些特点（Feature），或者已经对问题作出了部分假设，这些已知信息可以帮助我们进行预测。如果我们能够将这些先见性的知识融合起来，以便于获得 ML 的学习目标，这样的模型就是 Aggregation Model（聚合模型）。

现实生活中也有很多这样的例子，考虑这样的情形：当你想要购买一只股票，但不确定这只股票的未来涨跌，于是你向朋友们请教，根据他们的建议再做购买或放弃的抉择，那么我们如何参考他们的意见呢？有这样几种方法：

1. 选择过去预测最准确的朋友的建议，

   • 也就是 ML 中 Validation 效果最好的那个假设，
   • 写成数学形式：$G(\mathbf{x})=g_{t_{\ast }}(\mathbf{x})\text{ with }{t}_{\ast }=\underset{t\in \{1,2,...,T\}}{\mathrm{argmin}}{E}_{val}(g_t^{-})$ ，即从 $T$ 个假设（朋友的建议）中选择验证效果最佳（$E_{val}$ 最小）的假设；

2. 让朋友们对购买与否投票，然后平均地考虑投票结果，

   • 写成数学形式：$G(\mathbf{x})=\text{sign}\left(\sum _{t=1}^{T}1\cdot g_t(\mathbf{x})\right)$ ，这里 $g_t(\mathbf{x})\in \{-1,+1\}$ 分别代表不建议购买或建议购买；

3. 同样让朋友们投票，但不同的投票有不同的权重，

   • 写成数学形式：$G(\mathbf{x})=\text{sign}\left(\sum _{t=1}^T{\alpha }_t\cdot g_t(\mathbf{x})\right)\text{ with }{\alpha }_t\ge 0$ ，这里 ${\alpha }_t$ 的取值就是使得 $E_{val}$ 最小的权重组合；

4. 视情况而定，有选择地考虑部分建议，

   • 写成数学形式：$G(\mathbf{x})=\text{sign}\left(\sum _{t=1}^T{q}_t(\mathbf{x})\cdot g_t(\mathbf{x})\right)\text{ with }{q}_t(\mathbf{x})\ge 0$ ，这实际上是第三种方法的扩展（第三种方法分配好的权重是不变的）；

还有更多方法，在此暂不列举，后文我们会学到更多的聚合模型策略。

回想我们在 验证方法 一节中，我们也涉及到模型的选择，那么与聚合模型中的选取有什么区别呢？通过验证进行选择，可以公式化地描述为：$G(\mathbf{x})=g_{t_{\ast }}(\mathbf{x})\text{ with }{t}_{\ast }=\underset{t\in \{1,2,...,T\}}{\mathrm{argmin}}{E}_{val}(g_t^{-})$ ，这是非常简单且常见的选取策略，不过要实现这一目标，需要足够强力的假设 $g_t^{-}$ 使得 $E_{val}$ 足够小，以保证我们的模型可以对 $E_{out}$ 做到最好。

然而聚合模型中我们不必要求假设足够有力，而是集群体之智慧，取长补短。正如这样的情形：

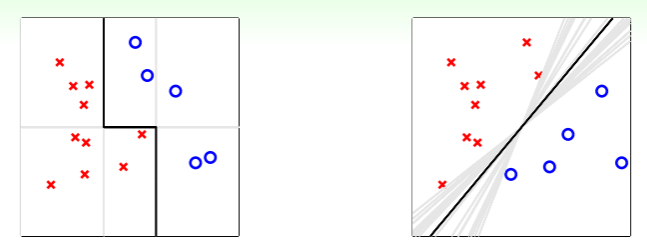
• 左图若是限制所有分类器必须横平竖直，即任何单个假设都不能有力地实现分类，但是若是我们结合多个假设的力量——取两个竖直的分类器和一个水平的分类器组合成一个折线的分类器，那么就可以做得足够好。在这里，聚合模型就像之前我们提到的特征转换策略，拓展了简单模型在复杂场景中的应用能力；
• 右图则是 PLA 的经典场景，《技法》的第一部分 SVM 中详细探讨了如何选择最佳的分类器，那么聚合模型会怎样做呢？实际上，由中心极限定理可知，对于无数的 PLA 分类器，我们无论如何为其赋予权重，最后得到的最佳假设都是趋向“中庸”的（即黑色直线代表的分类器处于有效分类器集合的中间）。这时，聚合模型做到了类似 large-margin 的 regulization 的效果；

关于中心极限定理

这是概率论中的知识，大意上讲如果一个结果是由大量不想干的原因累加导致，每个原因的作用范围又非常有限，那么最终的结果就会服从正态分布。

想要形象地理解，可以参考这个高尔顿板的示例程序： 运行结果如下：

练习：聚合模型的假设如何得出？

Uniform Blending

上面提到，我们公平地考虑每一份投票，然后综合起来做出抉择，这在 ML 中称为 uniform blending 。

blend 的本义是融合、交融，在此处就是均匀地进行融合。

利用 uniform blending 策略进行分类，就是对已知的假设 $g_t$ ，每个假设都有一份投票权，那么最终的抉择 $G(\mathbf{x})=\text{sign}\left(\sum _{t=1}^{T}1\cdot g_t(\mathbf{x})\right)$ ：

• 如果所有假设 $g_t$ 都一致，那自然别无选择；可若是假设各不相同，那么通过投票这样“民主”的考量，就可以实现少数服从多数、找到比较好的决策—— manjority can correct minority ；
• 如果要应用于多分类，则可以简单地扩展：$G(\mathbf{x})=\underset{1\le k\le K}{\mathrm{argmax}}\sum _{t=1}^T[g_t(\mathbf{x})=k]$ ；

利用 uniform blending 策略进行回归分析，则需要对所有投票进行平均：$G(\mathbf{x})=\frac{1}{T}\sum _{t=1}^T{g}_t(\mathbf{x})$ ：

• 同样，假设全部一致时只有唯一结果；而对于不同的假设时，有些假设的结果可能比目标结果大（即 $g_t(\mathbf{x})>f(\mathbf{x})$ ），有些则可能小，因此平均后的结果比单一假设得到的结果更加精确；
• 可以说，即使简单的 uniform blending 也会比单一的假设更佳。

如何从理论上证明 uniform blending 的优越性呢？我们考虑所有假设与目标假设之间的距离作为错误估计：

$$\begin{array}{rl}\text{avg}\left((g_t(\mathbf{x})-f(\mathbf{x}){)}^2\right)& =\text{avg}(g_t^2-2g_{t}f+f^2)\\ & =\text{avg}(g_t^2)-2Gf+f^2\\ & =\text{avg}(g_t^2)-G^2+G^2-2Gf+f^2\\ & =\text{avg}(g_t^2)-2G^2+G^2+(G-f{)}^2\\ & =\text{avg}(g_t^2-2g_{t}G+G^2)+(G-f{)}^2\\ & =\text{avg}((g_t-G{)}^2)+(G-f{)}^2\end{array}$$

这意味着对任意单个假设 $g_t$ ，其与“群体的智慧”—— $G$ 的差距期望满足：

$$\begin{array}{rlr}\text{avg}(E_{out}(g_t))& =\text{avg}\left(\mathbb{E}(g_t-G{)}^2\right)+& E_{out}(G)\\ & \Downarrow & \\ \text{avg}(E_{out}(g_t))& \ge & E_{out}(G)\end{array}$$

左边是单个假设的 $E_{out}$ ，它总是不小于群众智慧的 $E_{out}$ 。

因此，总的来考虑这样一个抽象的聚合模型训练流程：

1. 训练总共要进行 $T$ 轮，每一轮都需要规模为 $N$ 的数据集 ${\mathcal{D}}_t$ ，这些数据是独立同分布地产生自 $P^N$ ；
2. 每一轮通过学习算法 $\mathcal{A}({\mathcal{D}}_t)$ 获得一个最佳假设 $g_t$ ；

经过无限多轮的训练，我们将所有假设进行平均，则可以得到学习算法的期望：

$$\underset{T\to \infty }{\lim }G=\underset{T\to \infty }{\lim }\frac{1}{T}\sum _{t=1}^T{g}_t=\underset{\mathcal{D}}{\mathbb{E}}\mathcal{A}(\mathcal{D})$$

我们可以将其记作 $\bar{g}$ ，于是用其替代 $G$ ，可以得到：

$$\text{avg}(E_{out}(g_t))=\text{avg}\left(\mathbb{E}(g_t-\bar{g}{)}^2\right)+E_{out}(\bar{g})$$

这个式子左边是学习算法 $\mathcal{A}$ 在测试集上表现的期望，右边则是假设与共识 $\bar{g}$ 偏离程度的期望与共识 $\bar{g}$ 在测试集上表现的期望之和。通常在 ML 中将共识的性能称为 bias ，与共识的偏离程度的期望称为 variance 。而 uniform blending 在这里的作用，就是消除偏差，以获得更稳定、更优秀的共识。

练习：uniform blending 用于线性回归

Linear and Any Blending

如果我们为每个投票者分配不止一票，那么就可以看作对各自假设的加权，这是一种线性组合，因此称为 linear blending 。

利用 linear blending 进行分类，我们可以公式化描述为：

$$G(\mathbf{x})=\text{sign}\left(\sum _{t=1}^T{\alpha }_t\cdot g_t(\mathbf{x})\right)\text{ with }{\alpha }_t\ge 0$$

很自然地，我们想要得知最佳的票数分配，因此可以考虑使得训练时犯错最少的票数分配组合：$\underset{{\alpha }_t\ge 0}{\min }{E}_{in}(\mathbf{\alpha })$ 。

而若利用 linear blending 进行回归分析，要选择最佳的票数分配，我们考虑判断与实际的差距最小者：

$$\underset{{\alpha }_t\ge 0}{\min }\frac{1}{N}\sum _{n=1}^N{\left(y_n-\sum _{t=1}^T{\alpha }_t{g}_t({\mathbf{x}}_n)\right)}^2$$

这个式子似乎有些熟悉？我们在 probabilistic SVM 中先做一个 SVM 再做一个 logistic regression 时的 two-level learning ，在那里我们的最优化选择是：

$$\underset{w_i}{\min }\frac{1}{N}\sum _{n=1}^N{\left(y_n-\sum _{i=1}^{\tilde{d}}{w}_i{\varphi }_i({\mathbf{x}}_n)\right)}^2$$

因此，linear blending 其实可以看作线性模型、通过特征转换的假设集、部分限制的组合：

$$\text{linear blending=LinModel+hypotheses as transform+constraints}$$

不过与以往线性模型不同的是，我们这里有一个限制 ${\alpha }_t\ge 0$ ，不必惊慌，我们思考一下当 ${\alpha }_t<0$ 时意味着什么？指东往西！也就是说，我们可以将 ${\alpha }_t<0$ 的情况转换为 $|{\alpha }_t|$ 与 $-g_t(\mathbf{x})$ 的乘积——毕竟，二分类问题里99%的概率判断错误，那反过来不就是有 99%的概率排除错误选项吗？

不过在实际中，我们得到的假设不一定来自同一种模型，很有可能是在不同模型中训练得到最小 $E_{in}$ 的假设：$g_1\in {\mathcal{H}}_1,g_2\in {\mathcal{H}}_2,...,g_T\in {\mathcal{H}}_T$ 。不过我们需要知道几个特点：

• 我们已经知道，要从已经得到的假设里再挑出最好的假设，这是一个 best of best 的问题，因此时间代价是 $\mathcal{O}\left(d_{VC}\left(\bigcup _{t=1}^T{\mathcal{H}}_t\right)\right)$ ，这在大量模型中进行 blending 的开销可能超出我们的想象；
• 本节开头处我们就提到，selection 其实就是 blending 的一个特例——取 ${\alpha }_t=\min [E_{val}(g_t^{-})]$ ；
• 我们在 aggregation 中选取最佳模型时，要考量最小的 $E_{in}$ ，此时会再加上 best of best 的代价，使得最后的时间复杂度比 $\mathcal{O}\left(d_{VC}\left(\bigcup _{t=1}^T{\mathcal{H}}_t\right)\right)$ 更大，因此不建议使用 $E_{in}$ 作为衡量，而是使用验证犯错率 $E_{val}$ ——从 $E_{train}$ 中得到的 $g_t^{-}$ ；

Any Blending

因此对于从训练集 ${\mathcal{D}}_{train}$ 中获取的不同假设 $g_1^{-},g_2^{-},...,g_T^{-}$ ，我们可以通过特征转换将验证集 ${\mathcal{D}}_{val}$ 中的样本 $({\mathbf{x}}_n,y_n)$ 转换到更高维：$({\mathbf{z}}_n={\Phi }^{-}({\mathbf{x}}_n),y_n)$ ，此处 ${\Phi }^{-}(\mathbf{x})=(g_1^{-}(\mathbf{x}),...,g_T^{-}(\mathbf{x}))$ 。

于是 linear blending 的计算步骤是：

1. 在特征转换后的数据集上求解权重：$\mathbf{\alpha }=\text{LinearModel}(\{({\mathbf{z}}_n,y_n)\})$ ，
2. 然后返回 blending 的结果：$G_{LINB}(\mathbf{x})={\text{LinearHypothesis}}_{\alpha }(\text{innerprod}(\alpha ,\Phi (\mathbf{x})))$ ；

当然也可以选择非线性模型，这称之为 any blending （也称为 stacking ，取一层一层叠加之意）：

1. 在任意模型上计算假设：$\tilde{g}=\text{AnyModel}(\{({\mathbf{z}}_n,y_n)\})$ ，
2. 然后返回结果：$G_{ANYB}(\mathbf{x})=\tilde{g}(\Phi (\mathbf{x}))$ ；

这里要注意 $\Phi (\mathbf{x})=(g_1(\mathbf{x}),...,g_T(\mathbf{x}))$ 并没有 ${}^{-}$ 这个标号，这表明为了充分利用数据集，要在选择好假设后再次从训练集和验证集的并集中进行训练。

any blending 的优势就是更强大的适应性，它实现了因地制宜地 blending，不过正因如此也有过拟合的风险，需要小心。

blending 的时间代价是否值得？

林老师举了他在率队完成一个推荐系统的比赛时的例子，其中他利用两重 blending 使得最终得分远超竞争者： 实践中，blending 非常有效，尽管有计算负担，但也值得一试。

练习：使用 linear blending

Bagging (Bootstrap Aggregation)

blending 的前提是我们已经在不同模型中运算得到了一组假设，那么我们可否边求解假设时边进行聚合分析呢？

首先，我们知道学习假设 $g_t$ 时关键点就是要有差异（diversity），否则也就没有聚合的必要了。那么实现差异的策略有若干种：

1. 我们可以从不同的模型中学习：$g_1\in {\mathcal{H}}_1,g_2\in {\mathcal{H}}_2,...,g_T\in {\mathcal{H}}_T$ ；
2. 还可以设置不同的参数：例如梯度下降中的 $\eta =0.001,0.01,...,10,100$ ；
3. 也可以通过将学习算法随机化：比如为 PLA 算法设置随机的 seeds ；
4. 更可以直接从不同数据中进行求取：交叉验证中会将验证集从完整的数据集中抽取出来，因此得到的假设 $g_V^{-}$ 也有一定的随机性；

不过我们可否不将数据集缩小这种策略来实现数据随机导致的差异呢？重新回顾共识性能 bias 与偏离程度 variance —— 我们知道共识 $\bar{g}$ 比直接的学习算法 $\mathcal{A}(\mathcal{D})$ 性能更好，但是这对数据集的要求可能超过手头所拥有的，因此我们可以追求一种大致上类似的共识（approximate $\bar{g}$），它来自有限（尽管可能很大）的数据集 ${\mathcal{D}}_t$ ：

$$\text{approximate }{g}_t=\mathcal{A}({\mathcal{D}}_t)\text{ from }{\mathcal{D}}_t\sim P^N\text{ using only }\mathcal{D}$$

这就要用到统计学中的 bootstrapping 策略 —— 一种从数据集 $\mathcal{D}$ 中重采样获取 ${\mathcal{D}}_t$ 的方法，通常可以译作“自益”、“自助”：

• 它的原理很简单，就是从数据集 $\mathcal{D}$ 中抽样出 $N$ 个样本作为 ${\mathcal{D}}_1$ ，然后将这些样本放回原数据集，再次抽样得到 ${\mathcal{D}}_2$ …
• 这种 bootstrap aggregation 方法与之前提及的聚合方法不同：
• 通常将 bootstrap aggregation 称为 BAGging ，它是基算法 $\mathcal{A}$ 中的一种简单的 meta 算法；

通过使用 bootstrap aggregation ，原来二分类问题的分类器需要的迭代次数大大降低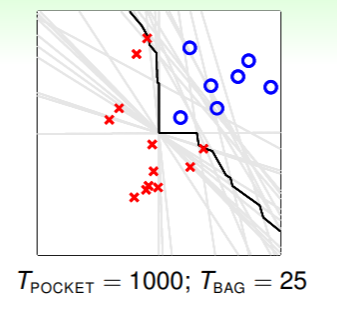： 这是由于通过 bagging 挑选出的假设 $g_t$ 的差异性非常令人满意，于是得到了正确的非线性分类器。实际上，只要基算法对数据的随机性足够敏感，那么差异性就会保证 bagging 策略足够有效、令人满意。

练习：bootstrap 策略两次踏入同一条河的概率