2010-final

散列

设散列表 H[] 容量 M=7，采用除留余数法（H(key) = key % M）确定地址，采用单向平方探测法解决冲突，即 H1 = (H(key) + 1^2 ) % M，H2 = (H(key) + 2^2 ) % M，……，Hk = (H(key) + k^2 ) % M，……。 现从空表开始依次插入关键码 {2010, 7, 4, 0}，试给出生成的散列表。

H[]:     0      1      2      3      4      5      6
key:     7     2010    0             4 

排序

对以下整型向量做就地堆排序，写出 Floyd 建堆法，以及各次迭代之后向量的内容。

rank :   0     1     2
vec[]:  16   2011    6

heap: 2011 16 6 iter1: 16 6 BBFABBA6;">2011 iter2: 6 BBFABBA6;">16 2011 iter3: BBFABBA6;">6 16 2011

图遍历

某有向图的邻接矩阵如下，现从顶点 1 出发做 DFS 遍历，遇多顶点歧义时编号小者优先。 试在右侧标出各边的分类结果（树边 T，前向边 F，后向边 B，跨边 C）

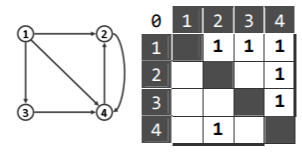
0  1  2  3  4
1     T  T  F
2           T
3           C
4     B

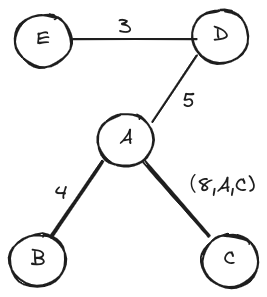
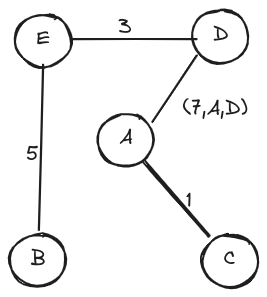
最小生成树

某无向网络及其邻接矩阵的上三角部分如下，现从顶点 A 出发采用 Prim 算法构造最小生成树，试在下三角区域标出树边及其被选用的次序。遇多边歧义时，按边端点合成数的字典序小者优先。

∞  A  B  C  D  E
A     9  1  7  7
B        7     5
C           7
D              3
E

∞  A  B  C  D  E
A     9  1  7  7
B        7     5
C  1        7
D  7           3
E     5        

注意：其中在加入第二条边时，有 4 条边的优先级数均为 7，对应的合成数为 (7, A, D) < (7, A, E) < (7, C, B) < (7, C, D) 故 (A, D) 被优先引入

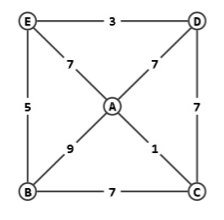
最短路径树

某无向网络及其邻接矩阵的上三角部分如下。现从顶点 A 出发采用 Dijkstra 算法构造最短路径生成树，试在下三角区域标出树边及其被选用的次序。遇多边歧义时，按边端点合成数的字典序小者优先。

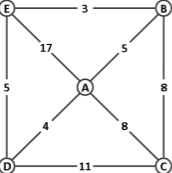
∞  A  B  C  D  E
A     5  8  4 17
B        8     3
C          11
D              5
E

∞  A  B  C  D  E
A     5  8  4 17
B  5     8     3
C  8       11
D  4           5
E     3

注意：在加入第三条边时，有两条边的优先级数均为 8，此时合成数为 (8, A, C)<(8, B, E)，故选择 (A, C)。