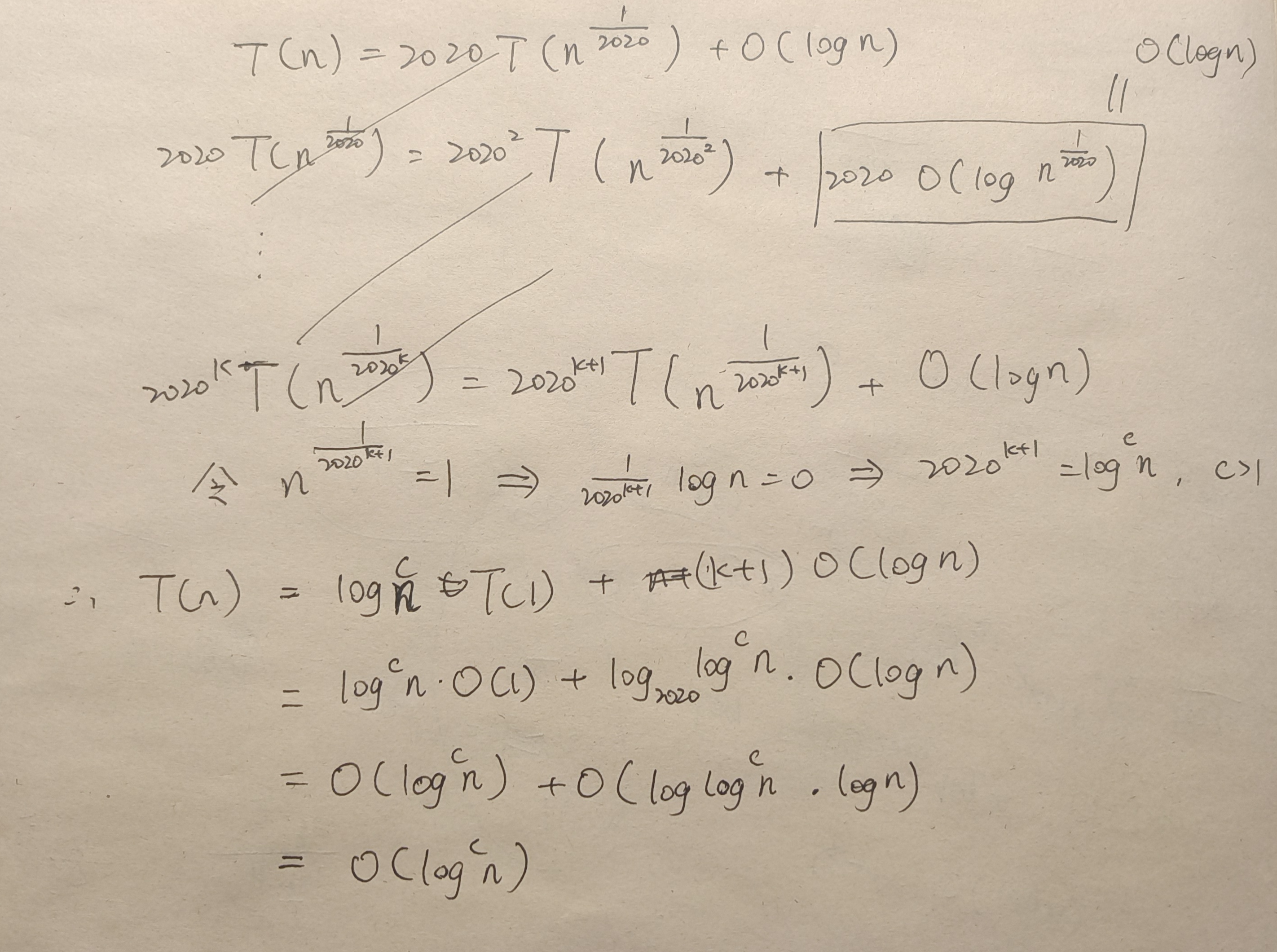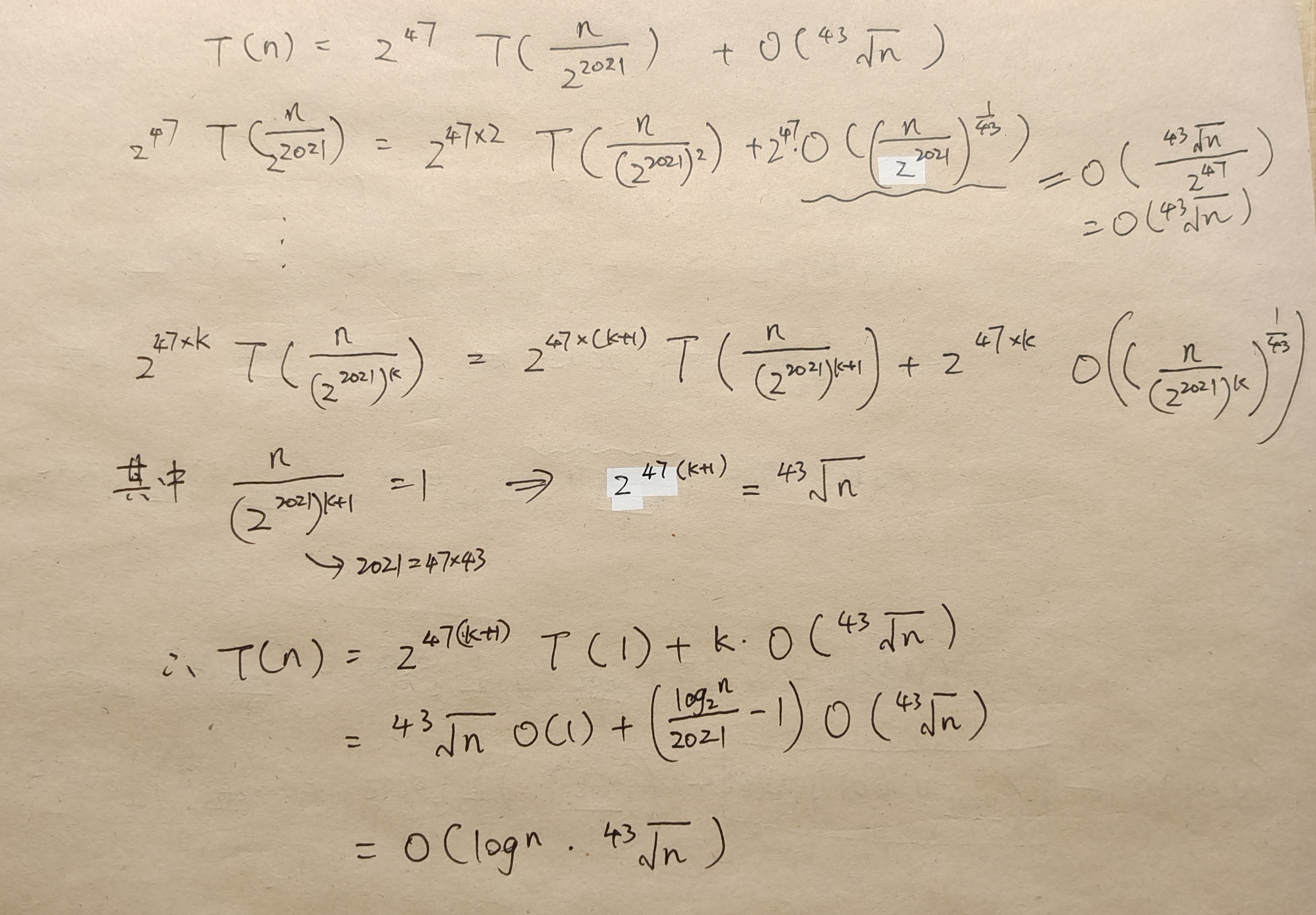2020_21-final

这一年只有回忆版，题目很不全，和官网样题合并一下。

简答

1. “在线”算法与“脱机”算法有何区别？

前者可以实时地执行，不必等待所有数据或指令归位。 后者反之。

2. 如何从 B-树中删除一个属于内部节点而非叶节点的关键码？

查找，删除，检测是否符合 B 树最小关键码数的要求，若不满足则分裂、下溢。

3. 按照 Tarjan 的定义，由 n 个节点组成的伸展树所具有的最大势能是多少？这类树是什么姿势？

$$\Phi (S)=\log (\prod _{v\in S}size(v))=\sum _{v\in S}\log (size(v))=\sum _{v\in S}rank(v)=\sum _{v\in S}\log V$$

势能的公式定义如上，因此 n 个节点的最大势能为 ${\Phi }_{max}(S)=\log n!=O(n\log n)$ 这种姿态是单调互异的序列、依次插入 Splay Tree 中得到的，形态是一条单链。

Complexity

试给出如下 T(n)的解析解，并说明理由：

$$T(n)=\{\begin{array}{rlr}& O(1)& (n\le 1)\\ & 2020\times T(n^{\frac{1}{2020}})+O(\log n)& (n\ge 2)\end{array}$$

$$T(n)=\{\begin{array}{rlr}& O(1)& (n\le 1)\\ & 2^{47}\times T(\frac{n}{2^{2021}})+O(\sqrt[43]{n})& (n\ge 2)\end{array}$$

RPN

将中缀表达式 (0!+1)*2^(3!+4)-(5!/6+(7-(8-9))) 转换为RPN。

0! 1 + 2 3! 4 + ^ * 5! 6 / 7 8 9 - - + -

Hash table

1. 一个容量 M=4079（素数）的哈希表，使用双向平方试探法，共插入了1231个词条，但在下一次插入时触发了 rehash 操作，问该哈希表此时的状态及 rehash 的原因。

4079 = 1019 * 4 + 3，因此双向平方试探可以填满整个哈希表，但是却发生了 rehash，说明装填因子高于 50%。

template <typename K, typename V>
bool Hashtable<K, V>::put( K k, V v ) { //散列表词条插入
	if ( ht[ probe4Hit( k ) ] ) return false; //雷同元素不必重复插入
	Rank r = probe4Free( k ); //为新词条找个空桶（只要装填因子控制得当，必然成功）
	ht[ r ] = new Entry<K, V>( k, v ); ++N; //插入
	if ( removed->test( r ) ) removed->clear( r );  //懒惰删除标记
	if ( (N + removed->size())*2 > M ) rehash(); //若装填因子高于50%，重散列
	return true;
}

指向原始笔记的链接

镜像地，删除操作时懒惰删除标记过多（超过 1/3 表长），则触发 rehash。

template <typename K, typename V> bool Hashtable<K, V>::remove( K k ) { //散列表词条删除算法
	int r = probe4Hit( k ); if ( !ht[r] ) return false; //确认目标词条确实存在
	release( ht[r] ); ht[r] = NULL; --N; //清除目标词条
	removed->set(r); //更新标记、计数器
	if ( removed->size() > 3*N ) rehash(); //若懒惰删除标记过多，重散列
	return true;
}

指向原始笔记的链接

2. 若采用“双向平方试探”策略的散列表长度取作 $M=2021$ ，则关键码 0 及其同义词所对应的试探链可记作：$a_0=b_0=0,a_1=1,b_1=2020,a_2=4,b_2=2017,...$ 试问：$\{a_i|i=0,1,2,3,...\}\cap \{b_j|j=0,1,2,3,...\}$ 除 0 以外，还包含哪些试探位置？为什么？

{an} = {0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,529,576,625,676,729,784,841,900,961,1024,1089,1156,1225,1296,1369,1444,1521,1600,1681,1764,1849,1936,}， {bn}={0,2020,2017,2012,2005,1996,1985,1972,1957,1940,1921,1900,1877,1852,1825,1796,1765,1732,1697,1660,1621,1580,1537,1492,1445,1396,1345,1292,1237,1180,1121,1060,997,932,865,796,725,652,577,500,421,340,257,172,85}

除 0之外，不包含相同的试探位置

KMP

给出下列模式串对应的 next[] 和改进后的 next[]。

     j:       0  1  2  3  4  5  6  7  8  9  10  11  12
   P[j]:      C  B  C  B  A  C  D  C  B  F   B   E   A
  next[j]:   -1  0  0  1  2  0  1  0  1  2   0   0   0
imp-next[j]: -1  0 -1  0  2 -1  1 -1  0  2   0   0   0

B-Tree

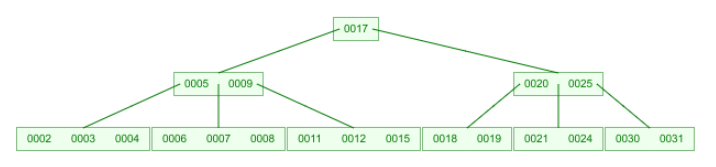
1. 2019 阶的 B 树 插入某关键码后树高增加，此时再次删除该关键码后树高一定降低? 给出证明或反例

否。 插入 22 后得到： 删除 22 后得到：

2. 2019阶的 B 树 删除某关键码后树高降低，此时再次插入该关键码后树高一定增加? 给出证明或反例

否。 删除 35 得到： 插入 35 得到：

QuickSelect

quickselect (A, k)中，给定 n 个数并随机置乱得到（无序）序列 $a_1,a_2,\dots ,a_n$，问

1. $a_i$ 与 $a_j$ 进行比较的概率（用 n, i, j, k 表示）；

不会。

Red-black Tree

红黑树结构，如果不显式记录颜色，通过隐式记录应该如何操作？

所谓节点颜色，本质上黑高度有关，维护高度

SubTree

二叉树 S, T 给出算法在 $O(S.size()+T.size())$ 内判断 S 是否为 T 中任一子树，节点只存了 rc, lc

1. 给出算法大概思路

利用二叉树的遍历序列+ KMP 算法匹配。 中序遍历+先序遍历可以唯一的确定一棵二叉树，因此这种算法的复杂度为：

• 中序遍历 S 和 T：$O(S.size()+T.size())$
• 先序遍历 S 和 T：$O(S.size()+T.size())$
• 以 S 的中序遍历序列为模式串，在 T 的中序遍历序列中检查：$O(S.size()+T.size())$
• 以 S 的先序遍历序列为模式串，在 T 的先序遍历序列中检查：$O(S.size()+T.size())$
• 如果中序遍历序列和先序遍历序列的检查都成功，说明存在。

2. 写出并说明你的算法

3. 证明你的算法是对的

Geometric Series

在本课的学习中，曾出现过许多利用几何分布（算法执行到下一步停止的概率为 p）进行计算的实例，请举出 4 处并简要说明之。

1. 跳转表的高度
2. 模式匹配的暴力算法的性能分析
3. 堆的上滤
4. 快排中 pivot 的选择

Sort

长度为2020的序列仅能用交换进行排序，最坏情况下至少要交换几次? 为什么?

以循环节做考量，选择排序的思路就是选择 unsorted 区间内最大者，与 unsorted 区间的最后一个元素交换，使得 sorted 区间长度+1。

这反映在循环节的表现，即是 unsorted 区间的最大者 M 脱离所属的循环节，在sorted区间内自成一个单元素的循环节，而 M 原来的循环节长度-1。

初始时，sorted 区间长度为 0，其包含的单元素循环节数量也为 0，每一轮扫描、交换，都会使得 sorted 区间+1，同样地其中单元素循环节的数量也+1。迭代循环下去，直到最后一轮，一次交换使得 2个单元素循环节归位，因此总共至少需要交换 2020-1=2019次。

Reconstruction Binary Tree

// 由先序、中序遍历序列，重构一棵由n个节点组成的二叉树 
BinNodePosi reconstruct( T pre[], T in[], int n ) {
	if ( n < 1 ) return NULL;
	k = search( pre[0], in, n ); //locate pre[0] in in[] by SEQUENTIAL search
	return new BinNode(
				pre[a], //key
				reconstruct( , , ) //left subtree
				reconstruct( , , ) //right subtree
			);
}

1. 试补全递归调用处缺失的参数；

2. 设每次 search ()的返回值随机分布于 [0,n)，试估计算法的期望时间复杂度。