🌰Senjl's Digital Garden🐉

Recent writing

Insertion in a Red-Black Tree

37分钟阅读

Introduction

Red-Black tree is a self-balancing binary search tree in which each node contains an extra bit for denoting the color of the node, either red or black.

A red-black tree satisfies the following properties:

  1. Red/Black Property: Every node is colored, either red or black.
  2. Root Property: The root is black.
  3. Leaf Property: Every leaf (NIL) is black.
  4. Red Property: If a red node has children then, the children are always black.
  5. Depth Property: For each node, any simple path from this node to any of its descendant leaf has the same black-depth (the number of black nodes).

An example of a red-black tree is:

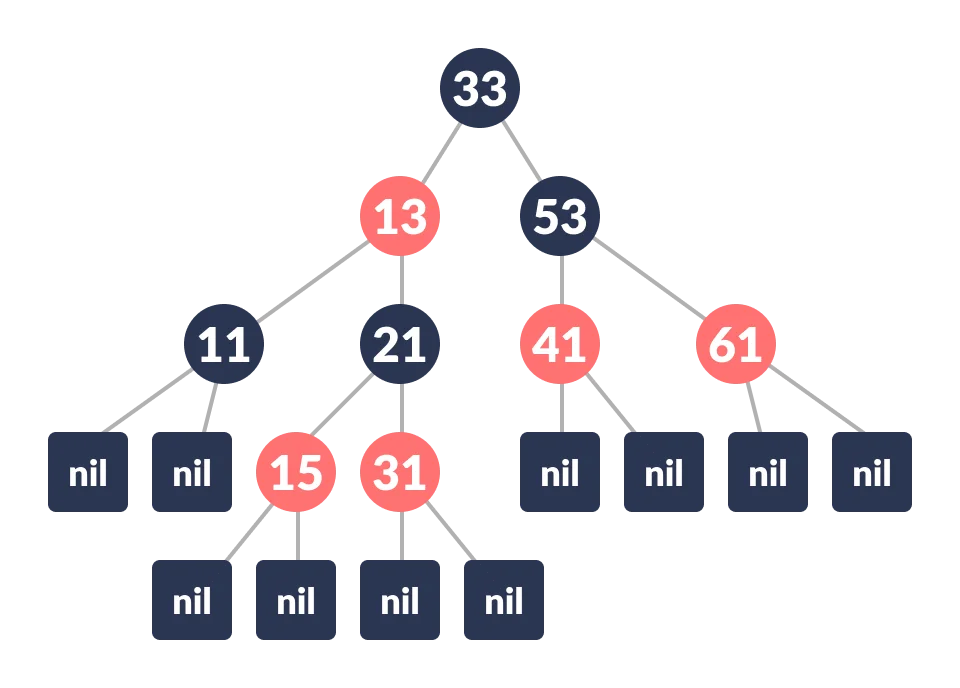
Each node has the following attributes:

  • color
  • key
  • leftChild
  • rightChild
  • parent (except root node)

[! question] How the red-black tree maintains the property of self-balancing?

The red-black color is meant for balancing the tree.

The limitations put on the node colors ensure that any simple path from the root to a leaf is not more than twice as long as any other such path. It helps in maintaining the self-balancing property of the red-black tree.

Operations on a Red-Black Tree

Various operations that can be performed on a red-black tree are:

Rotating the subtrees

In rotation operation, the positions of the nodes of a subtree are interchanged.

Rotation operation is used for maintaining the properties of a red-black tree when they are violated by other operations such as insertion and deletion.

There are two types of rotations:

Left Rotate

In left-rotation, the arrangement of the nodes on the right is transformed into the arrangements on the left node.

Algorithm

  1. Let the initial tree be:

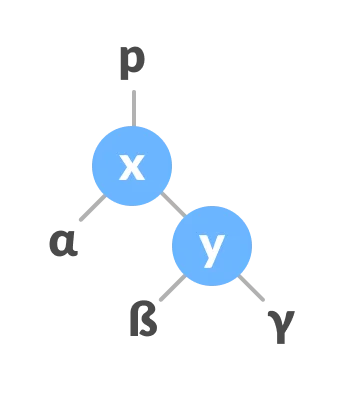
  2. If y has a left subtree, assign x as the parent of the left subtree of y.

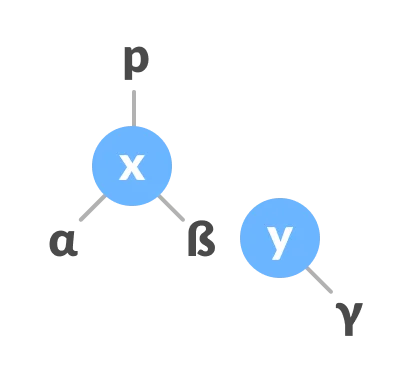
  1. If the parent of x is NULL, make y as the root of the tree.
  2. Else if x is the left child of p, make y as the left child of p.
  3. Else assign y as the right child of p.

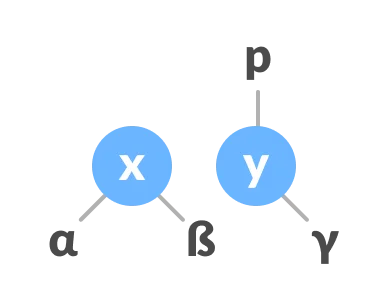
  1. Make y as the parent of x.

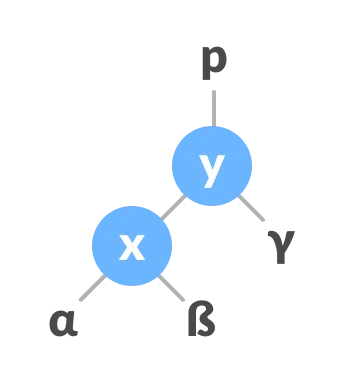
Right Rotate

In right-rotation, the arrangement of the nodes on the left is transformed into the arrangements on the right node.

  1. Let the initial tree be:

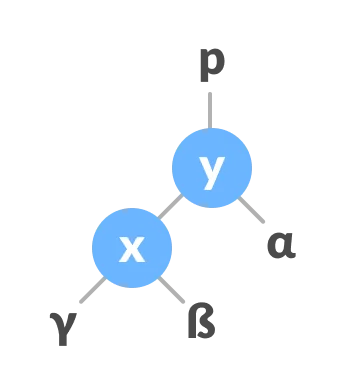
  2. If x has a right subtree, assign y as the parent of the right subtree of x.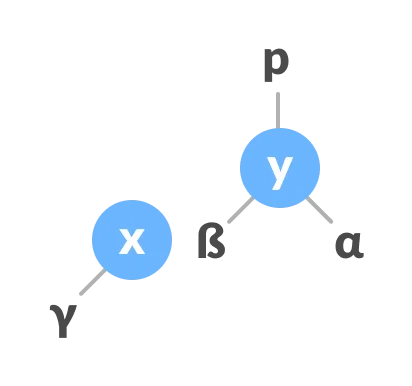

  3. If the parent of y is NULL, make x as the root of the tree.

  4. Else if y is the right child of its parent p, make x as the right child of p.

  5. Else assign x as the left child of p.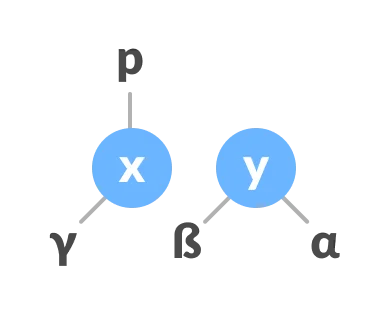

  6. Make x as the parent of y.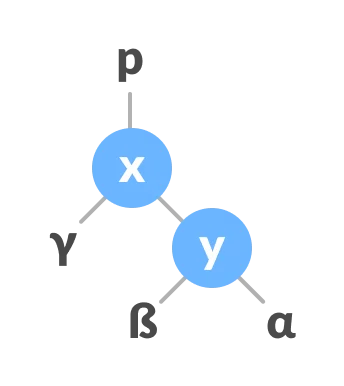

Left-Right and Right-Left Rotate

In left-right rotation, the arrangements are first shifted to the left and then to the right.

  1. Do left rotation on x-y.

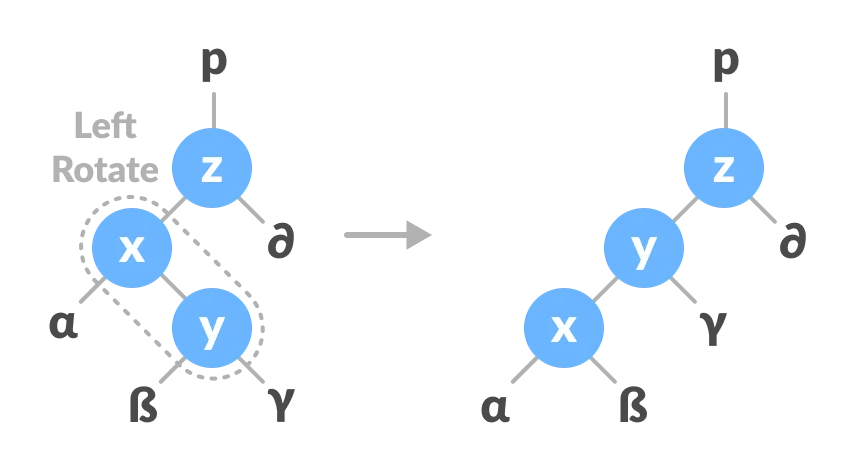
  2. Do right rotation on y-z.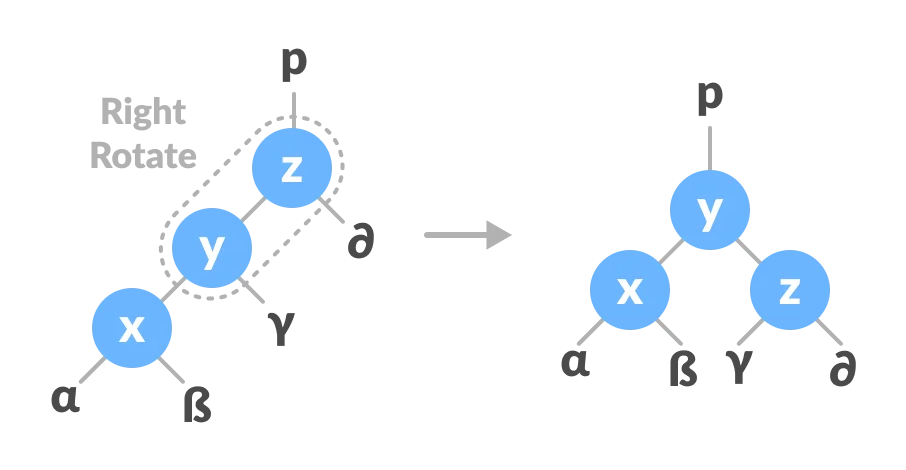

In right-left rotation, the arrangements are first shifted to the right and then to the left.

  1. Do right rotation on x-y.

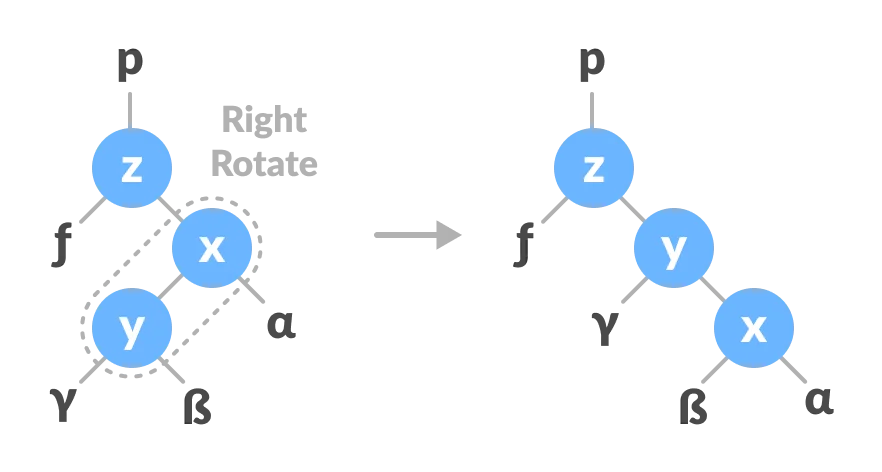
  2. Do left rotation on z-y.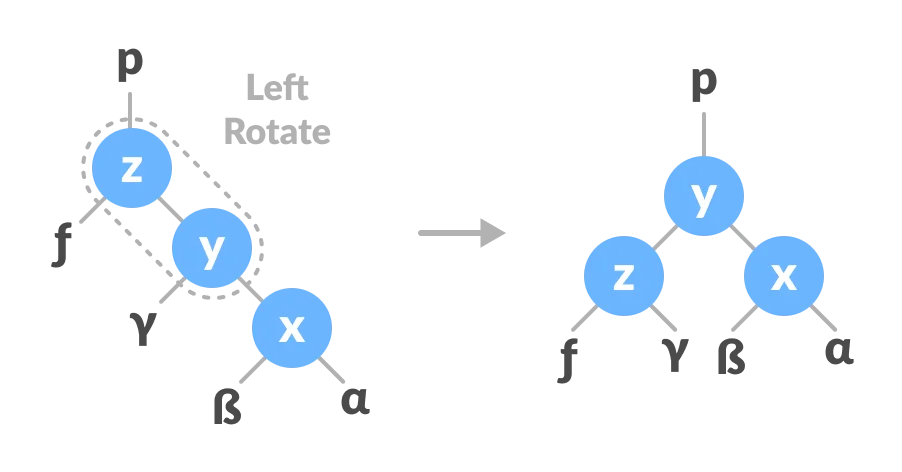

Inserting an element

While inserting a new node, the new node is always inserted as a RED node. After insertion of a new node, if the tree is violating the properties of the red-black tree then, we do the following operations.

  1. Recolor
  2. Rotation

Algorithm to insert a node

Following steps are followed for inserting a new element into a red-black tree:

  1. Let y be the leaf (ie. NIL) and x be the root of the tree.
  2. Check if the tree is empty (ie. whether x is NIL). If yes, insert newNode as a root node and color it black.
  3. Else, repeat steps following steps until leaf (NIL) is reached.
    1. Compare newKey with rootKey.
    2. If newKey is greater than rootKey, traverse through the right subtree.
    3. Else traverse through the left subtree.
  4. Assign the parent of the leaf as a parent of newNode.
  5. If leafKey is greater than newKey, make newNode as rightChild.
  6. Else, make newNode as leftChild.
  7. Assign NULL to the left and rightChild of newNode.
  8. Assign RED color to newNode.
  9. Call InsertFix-algorithm to maintain the property of red-black tree if violated.

[! note] Why newly inserted nodes are always red in a red-black tree?

This is because inserting a red node does not violate the depth property of a red-black tree.

If you attach a red node to a red node, then the rule is violated but it is easier to fix this problem than the problem introduced by violating the depth property.

Algorithm to maintain red-black property after insertion

This algorithm is used for maintaining the property of a red-black tree if the insertion of a newNode violates this property.

  1. Do the following while the parent of newNode p is RED.

  2. If p is the left child of grandParent gP of z, do the following.

    • Case-I:
      1. If the color of the right child of gP of z is RED, set the color of both the children of gP as BLACK and the color of gP as RED.
      2. Assign gP to newNode.
    • Case-II:
      1. Else if newNode is the right child of p then, assign p to newNode.
      2. Left-Rotate newNode.
    • Case-III:
      1. Set color of p as BLACK and color of gP as RED.
      2. Right-Rotate gP.

  3. Else, do the following.

    1. If the color of the left child of gP of z is RED, set the color of both the children of gP as BLACK and the color of gP as RED.
    2. Assign gP to newNode.
    3. Else if newNode is the left child of p then, assign p to newNode and Right-Rotate newNode.
    4. Set color of p as BLACK and color of gP as RED.
    5. Left-Rotate gP.

  4. Set the root of the tree as BLACK.

Deleting an element from a Red-Black Tree

This operation removes a node from the tree. After deleting a node, the red-black property is maintained again.

Algorithm to delete a node

  1. Save the color of nodeToBeDeleted in origrinalColor.
  2. If the left child of nodeToBeDeleted is NULL
    1. Assign the right child of nodeToBeDeleted to x.
    2. Transplant nodeToBeDeleted with x.
  3. Else if the right child of nodeToBeDeleted is NULL
    1. Assign the left child of nodeToBeDeleted into x.
    2. Transplant nodeToBeDeleted with x.
  4. Else
    1. Assign the minimum of right subtree of noteToBeDeleted into y.
    2. Save the color of y in originalColor.
    3. Assign the rightChild of y into x.
    4. If y is a child of nodeToBeDeleted, then set the parent of x as y.
    5. Else, transplant y with rightChild of y.
    6. Transplant nodeToBeDeleted with y.
    7. Set the color of y with originalColor.
  5. If the originalColor is BLACK, call DeleteFix (x).

Algorithm to maintain Red-Black property after deletion

This algorithm is implemented when a black node is deleted because it violates the black depth property of the red-black tree.

This violation is corrected by assuming that node x (which is occupying y’s original position) has an extra black. This makes node x neither red nor black. It is either doubly black or black-and-red. This violates the red-black properties.

However, the color attribute of x is not changed rather the extra black is represented in x’s pointing to the node.

The extra black can be removed if

  1. It reaches the root node.
  2. If x points to a red-black node. In this case, x is colored black.
  3. Suitable rotations and recoloring are performed.

The following algorithm retains the properties of a red-black tree.

  1. Do the following until the x is not the root of the tree and the color of x is BLACK
  2. If x is the left child of its parent then,
    1. Assign w to the sibling of x.
    2. If the right child of parent of x is RED,
      Case-I:
      1. Set the color of the right child of the parent of x as BLACK.
      2. Set the color of the parent of x as RED.
      3. Left-Rotate the parent of x.
      4. Assign the rightChild of the parent of x to w.
    3. If the color of both the right and the leftChild of w is BLACK,
      Case-II:
      1. Set the color of w as RED
      2. Assign the parent of x to x.
    4. Else if the color of the rightChild of w is BLACK
      Case-III:
      1. Set the color of the leftChild of w as BLACK
      2. Set the color of w as RED
      3. Right-Rotate w.
      4. Assign the rightChild of the parent of x to w.
    5. If any of the above cases do not occur, then do the following.
      Case-IV:
      1. Set the color of w as the color of the parent of x.
      2. Set the color of the parent of x as BLACK.
      3. Set the color of the right child of w as BLACK.
      4. Left-Rotate the parent of x.
      5. Set x as the root of the tree.
  3. Else the same as above with right changed to left and vice versa.
  4. Set the color of x as BLACK.

Please refer to insertion and deletion operations for more explanation with examples.

Illustration

Insert

Red-Black tree is a self-balancing binary search tree in which each node contains an extra bit for denoting the color of the node, either red or black.

Before reading this article, please refer to the article on red-black tree.

While inserting a new node, the new node is always inserted as a RED node. After insertion of a new node, if the tree is violating the properties of the red-black tree then, we do the following operations.

  1. Recolor
  2. Rotation

Algorithm to Insert a New Node

Following steps are followed for inserting a new element into a red-black tree:

  1. The newNode be:

    New node

  2. Let y be the leaf (ie. NIL) and x be the root of the tree. The new node is inserted in the following tree.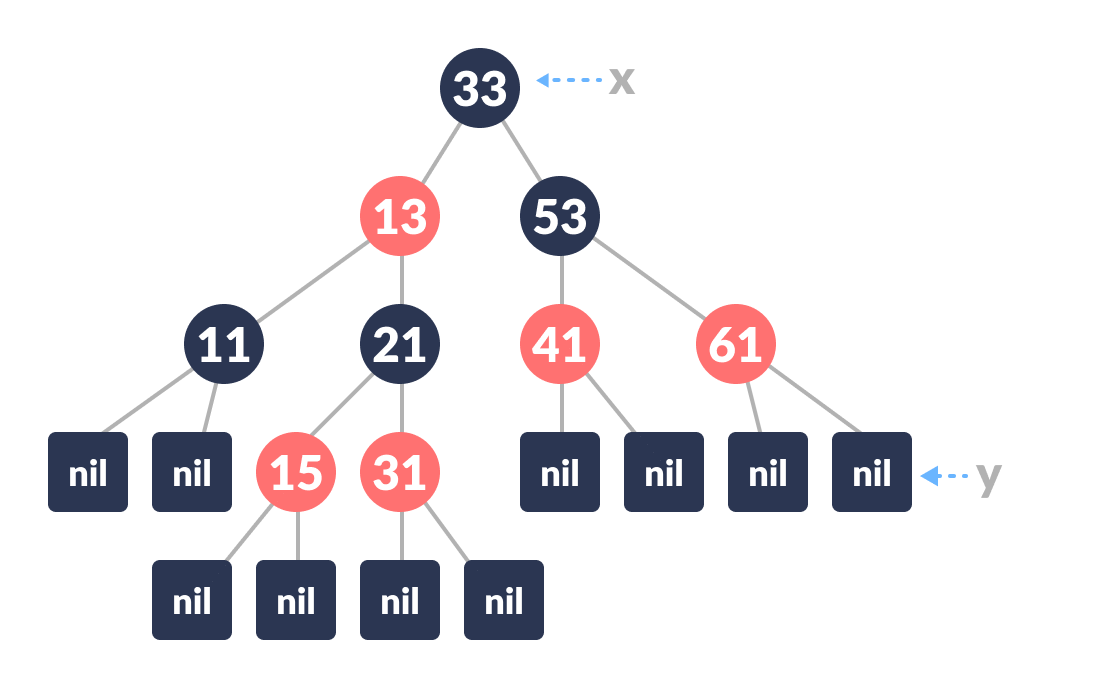

    Initial tree

  3. Check if the tree is empty (ie. whether x is NIL). If yes, insert newNode as a root node and color it black.

  4. Else, repeat steps following steps until leaf (NIL) is reached.

    1. Compare newKey with rootKey.

    2. If newKey is greater than rootKey, traverse through the right subtree.

    3. Else traverse through the left subtree.

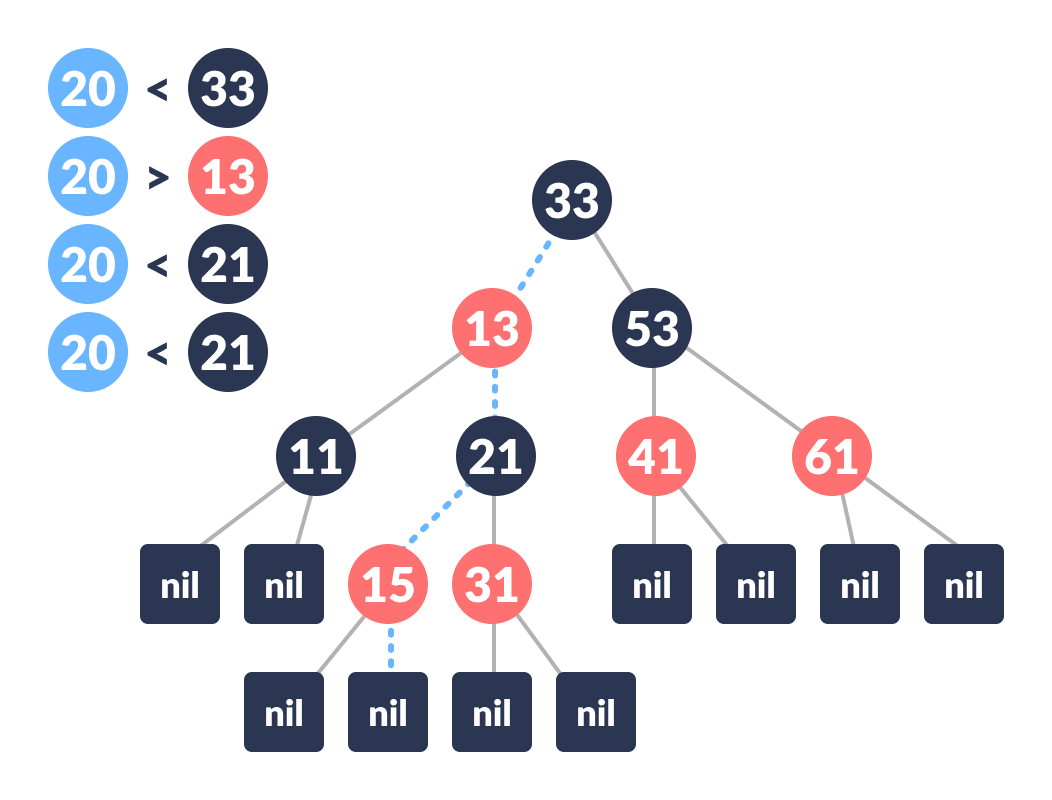
      Path leading to the node where newNode is to be inserted

  5. Assign the parent of the leaf as parent of newNode.

  6. If leafKey is greater than newKey, make newNode as rightChild.

  7. Else, make newNode as leftChild.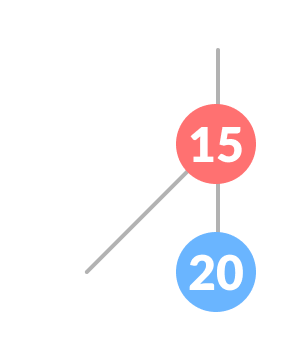

    New node inserted

  8. Assign NULL to the left and rightChild of newNode.

  9. Assign RED color to newNode.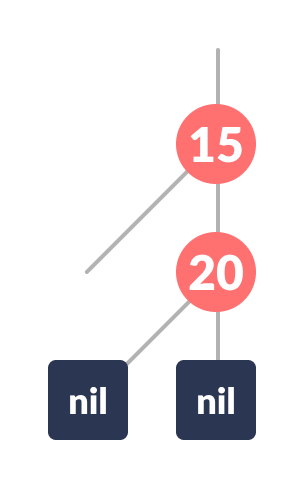

    Set the color of the newNode red and assign null to the children

  10. Call InsertFix-algorithm to maintain the property of red-black tree if violated.

Why newly inserted nodes are always red in a red-black tree?

This is because inserting a red node does not violate the depth property of a red-black tree.

If you attach a red node to a red node, then the rule is violated but it is easier to fix this problem than the problem introduced by violating the depth property.

Algorithm to Maintain Red-Black Property After Insertion

This algorithm is used for maintaining the property of a red-black tree if insertion of a newNode violates this property.

  1. Do the following until the parent of newNode p is RED.

  2. If p is the left child of grandParent gP of newNode, do the following.
    Case-I:

    1. If the color of the right child of gP of newNode is RED, set the color of both the children of gP as BLACK and the color of gP as RED.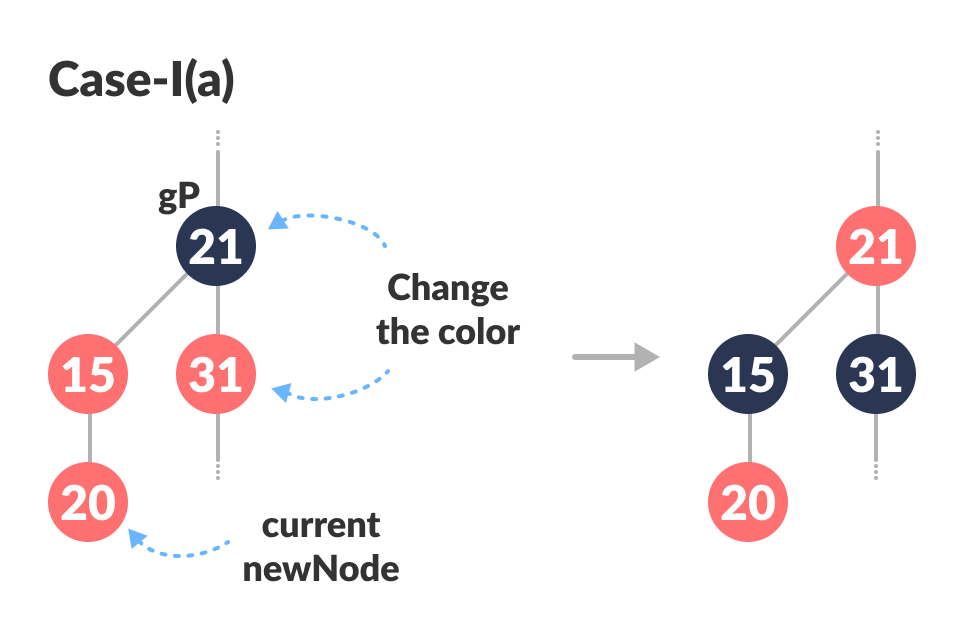

      Color change

    2. Assign gP to newNode.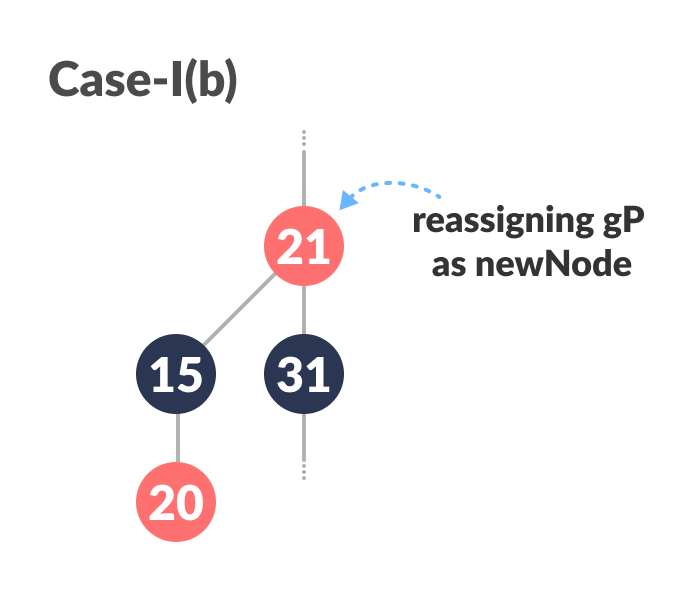

      Reassigning newNode

      Case-II:

    3. (Before moving on to this step, while loop is checked. If conditions are not satisfied, it the loop is broken.)
      Else if newNode is the right child of p then, assign p to newNode.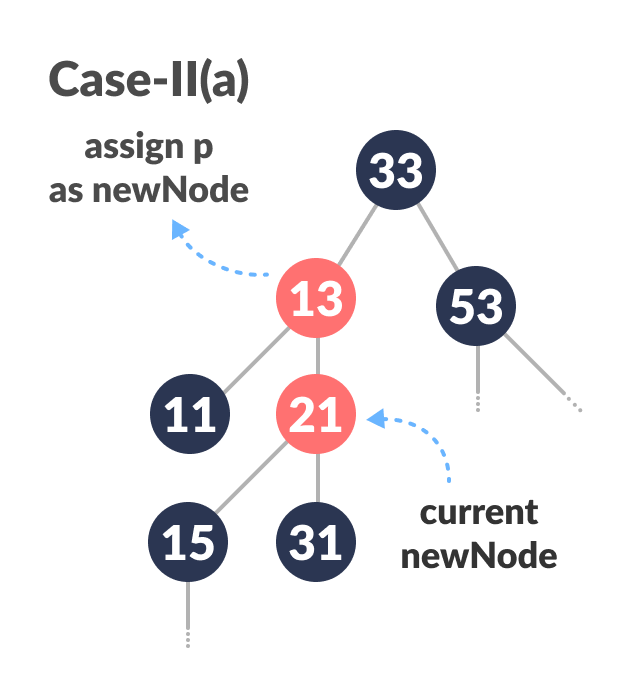

      Assigning parent of newNode as newNode

    4. Left-Rotate newNode.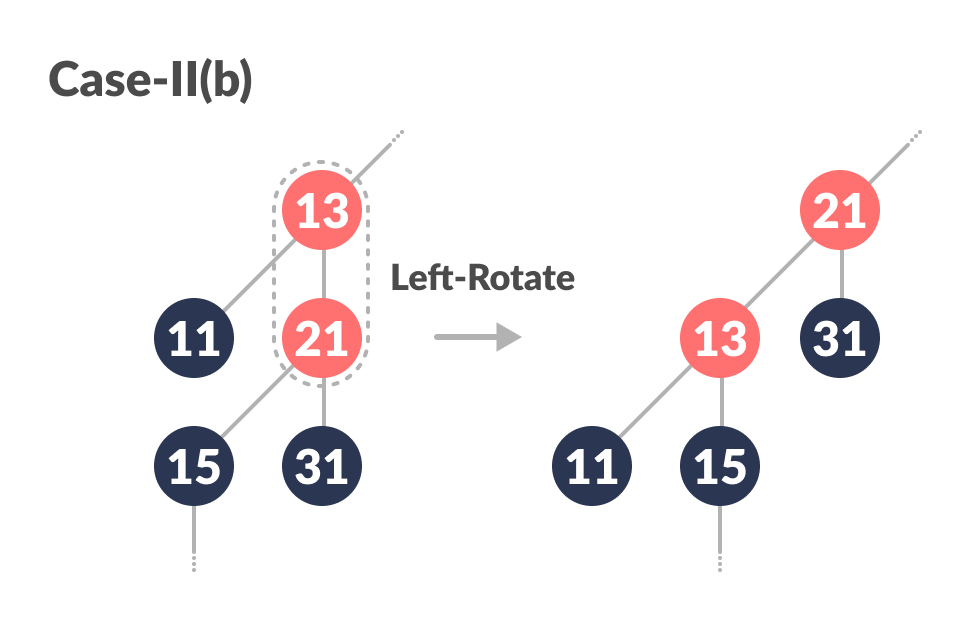

      Left Rotate

      Case-III:

    5. (Before moving on to this step, while loop is checked. If conditions are not satisfied, it the loop is broken.)
      Set color of p as BLACK and color of gP as RED.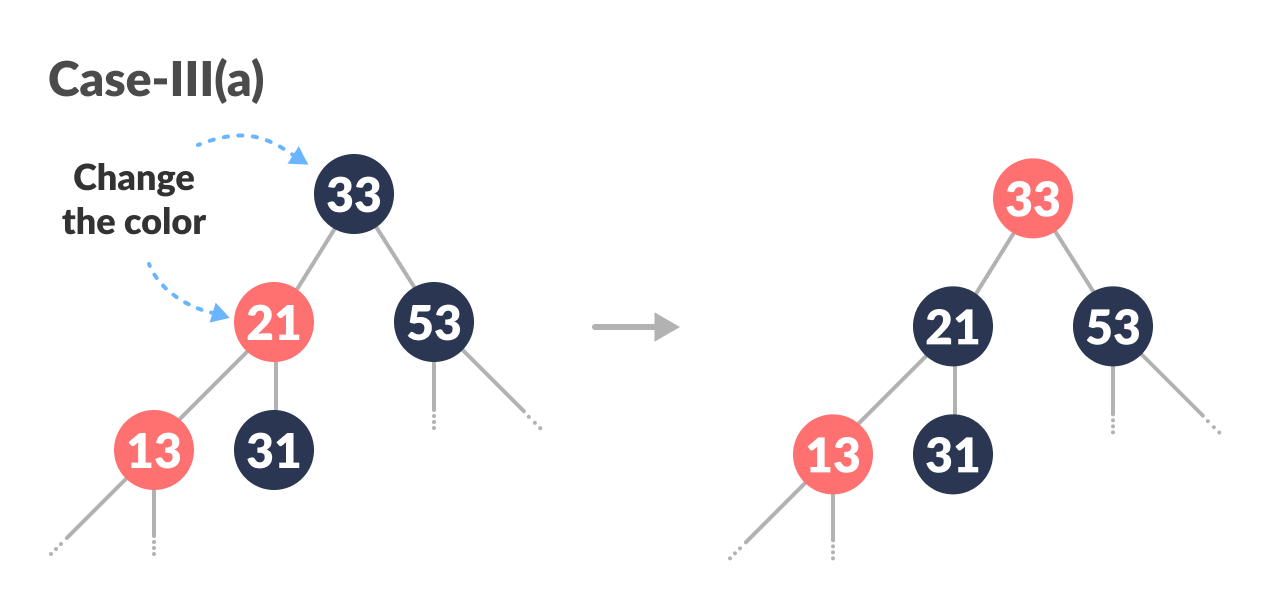

      Color change

    6. Right-Rotate gP.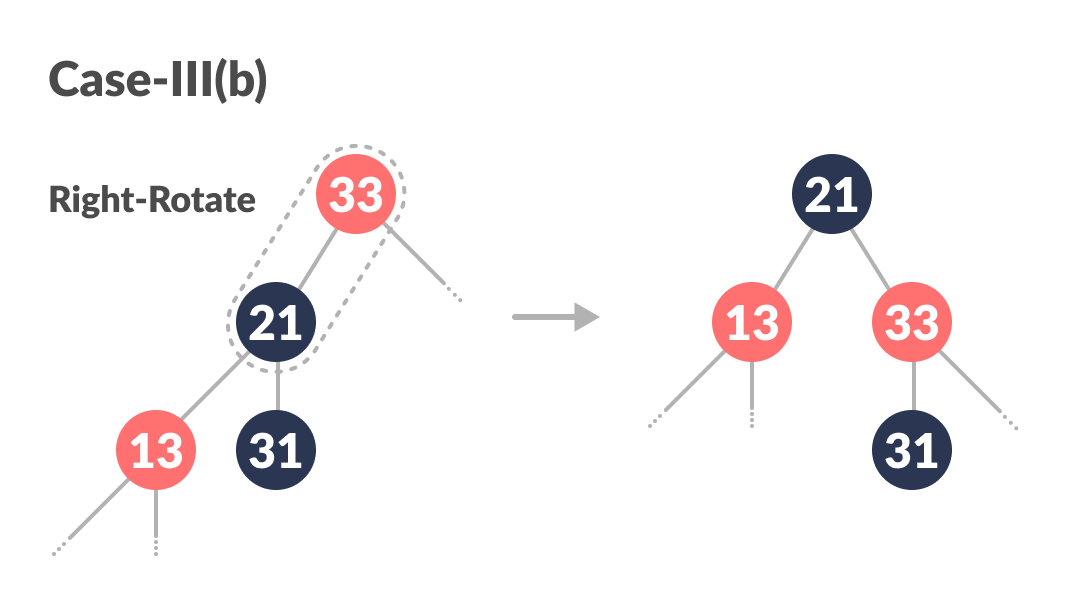

      Right Rotate

  3. Else, do the following.

    1. If the color of the left child of gP of z is RED, set the color of both the children of gP as BLACK and the color of gP as RED.
    2. Assign gP to newNode.
    3. Else if newNode is the left child of p then, assign p to newNode and Right-Rotate newNode.
    4. Set color of p as BLACK and color of gP as RED.
    5. Left-Rotate gP.

  4. (This step is performed after coming out of the while loop.)
    Set the root of the tree as BLACK.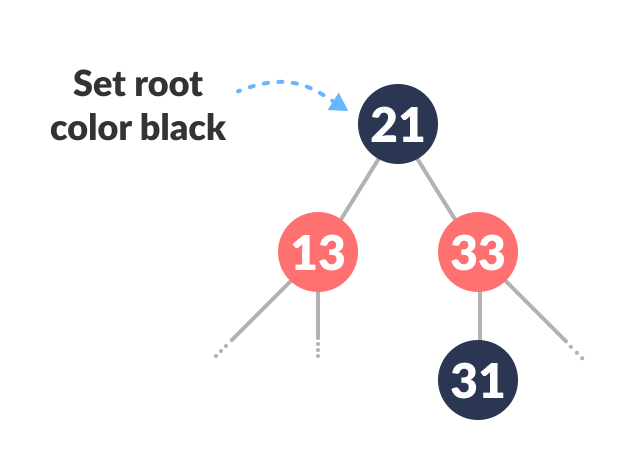

    Set root’s color black

The final tree look like this:

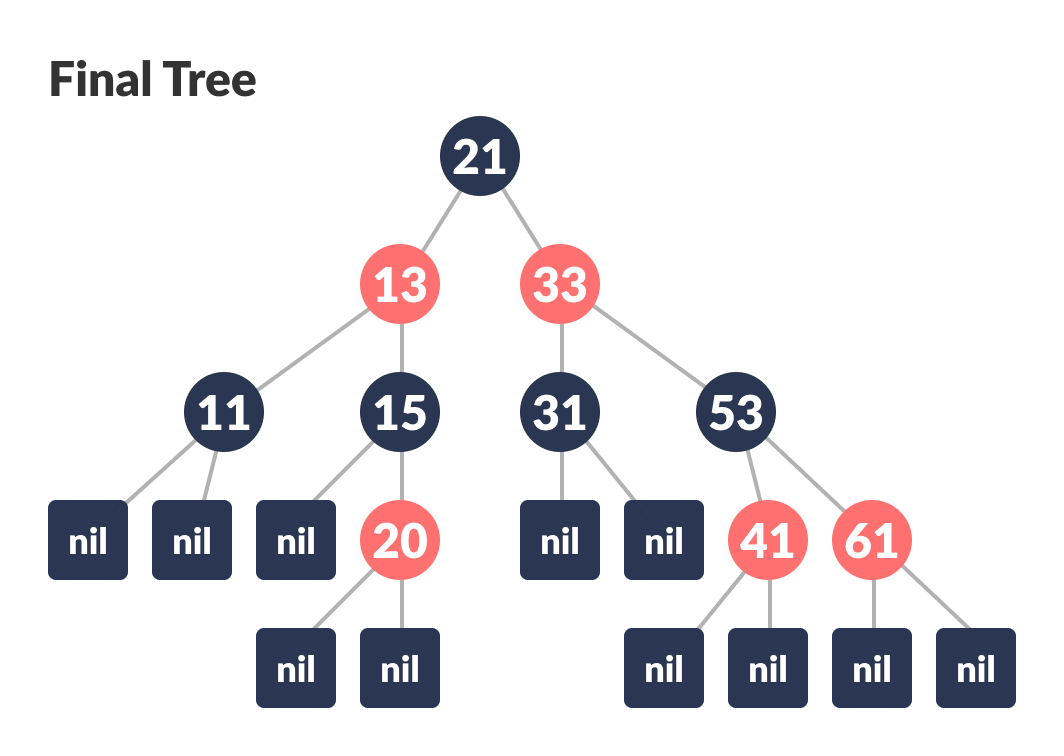
Final tree

Delete

Red-Black tree is a self-balancing binary search tree in which each node contains an extra bit for denoting the color of the node, either red or black.

Before reading this article, please refer to the article on red-black tree.

Deleting a node may or may not disrupt the red-black properties of a red-black tree. If this action violates the red-black properties, then a fixing algorithm is used to regain the red-black properties.

Deleting an element from a Red-Black Tree

This operation removes a node from the tree. After deleting a node, the red-black property is maintained again.

  1. Let the nodeToBeDeleted be: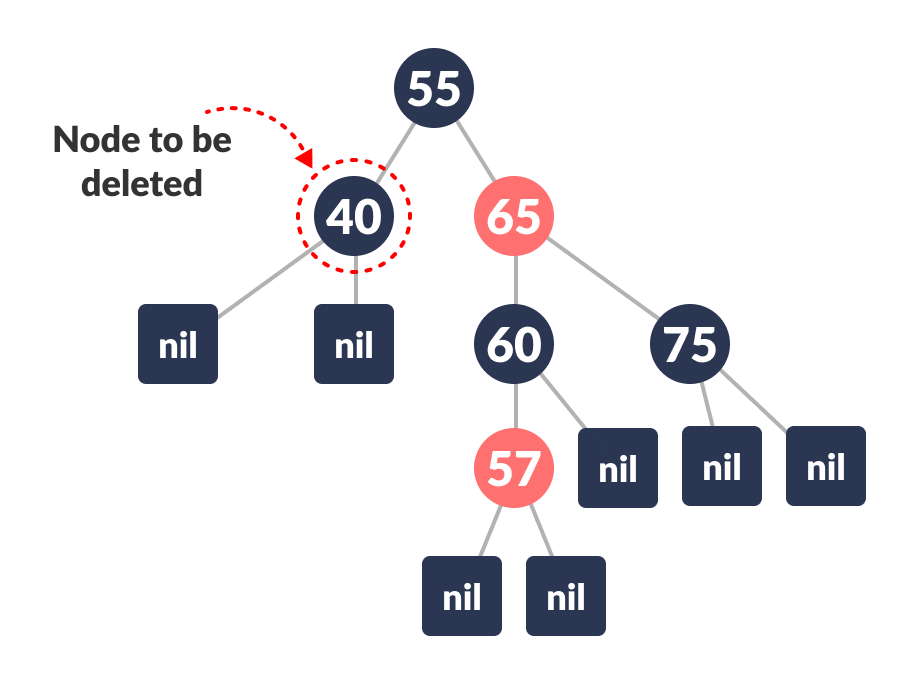

    Node to be deleted

  2. Save the color of nodeToBeDeleted in origrinalColor.

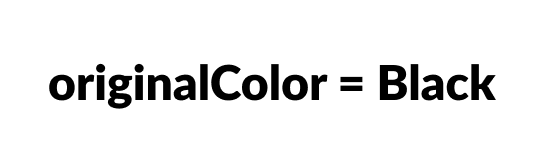
    Saving original color

  3. If the left child of nodeToBeDeleted is NULL

    1. Assign the right child of nodeToBeDeleted to x.

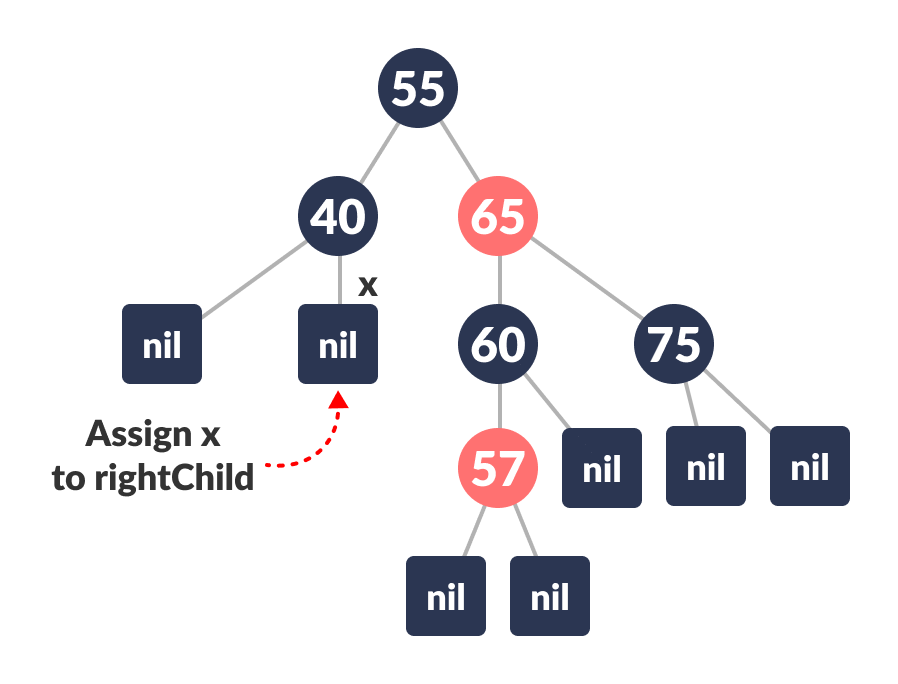
      Assign x to the rightChild

    2. Transplant nodeToBeDeleted with x.

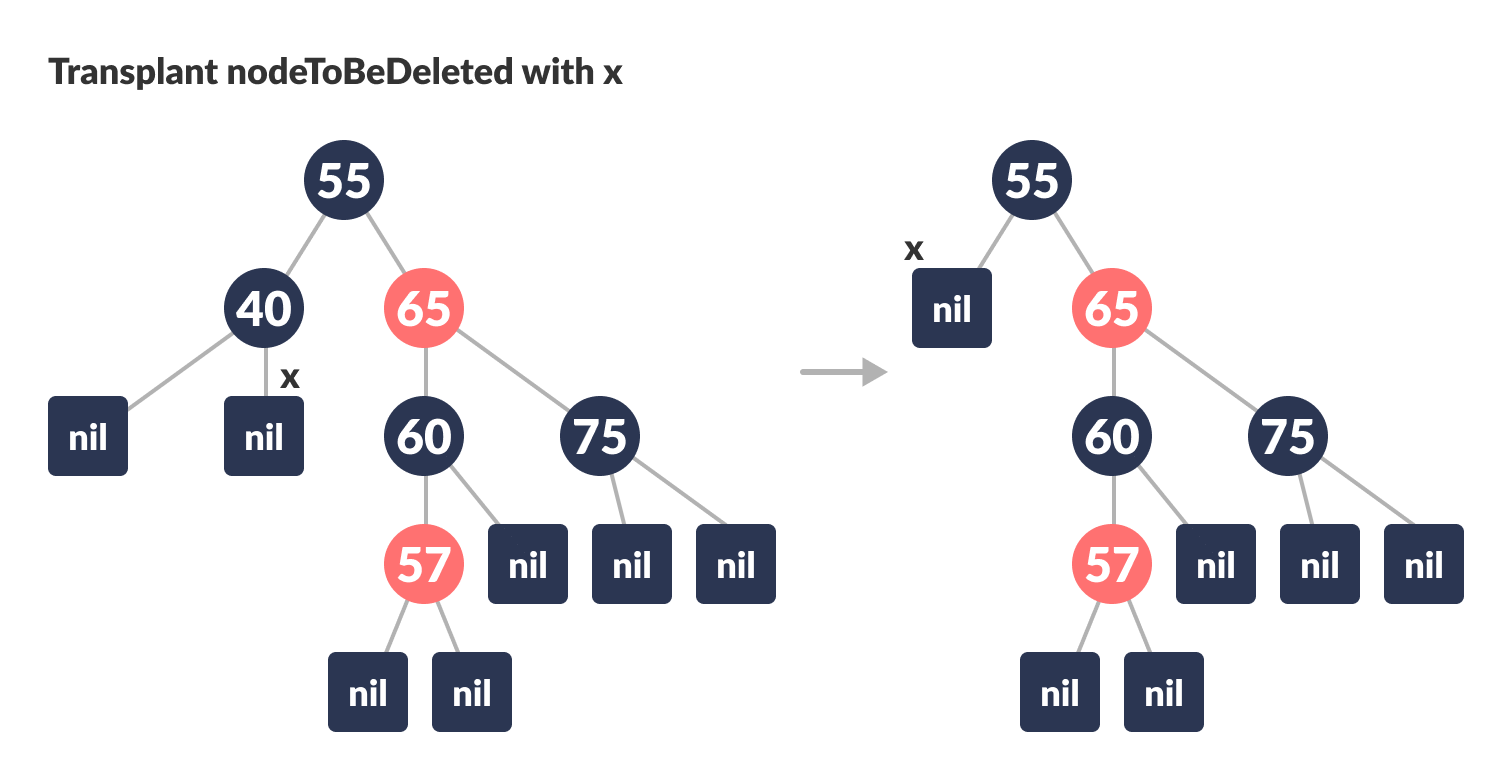
      Transplant nodeToBeDeleted with x

  4. Else if the right child of nodeToBeDeleted is NULL

    1. Assign the left child of nodeToBeDeleted into x.
    2. Transplant nodeToBeDeleted with x.

  5. Else

    1. Assign the minimum of right subtree of noteToBeDeleted into y.
    2. Save the color of y in originalColor.
    3. Assign the rightChild of y into x.
    4. If y is a child of nodeToBeDeleted, then set the parent of x as y.
    5. Else, transplant y with rightChild of y.
    6. Transplant nodeToBeDeleted with y.
    7. Set the color of y with originalColor.

  6. If the originalColor is BLACK, call DeleteFix(x).

Algorithm to maintain Red-Black property after deletion

This algorithm is implemented when a black node is deleted because it violates the black depth property of the red-black tree.

This violation is corrected by assuming that node x (which is occupying y’s original position) has an extra black. This makes node x neither red nor black. It is either doubly black or black-and-red. This violates the red-black properties.

However, the color attribute of x is not changed rather the extra black is represented in x’s pointing to the node.

The extra black can be removed if

  1. It reaches the root node.
  2. If x points to a red-black node. In this case, x is colored black.
  3. Suitable rotations and recolorings are performed.

Following algorithm retains the properties of a red-black tree.

  1. Do the following until the x is not the root of the tree and the color of x is BLACK
  2. If x is the left child of its parent then,

    1. Assign w to the sibling of x.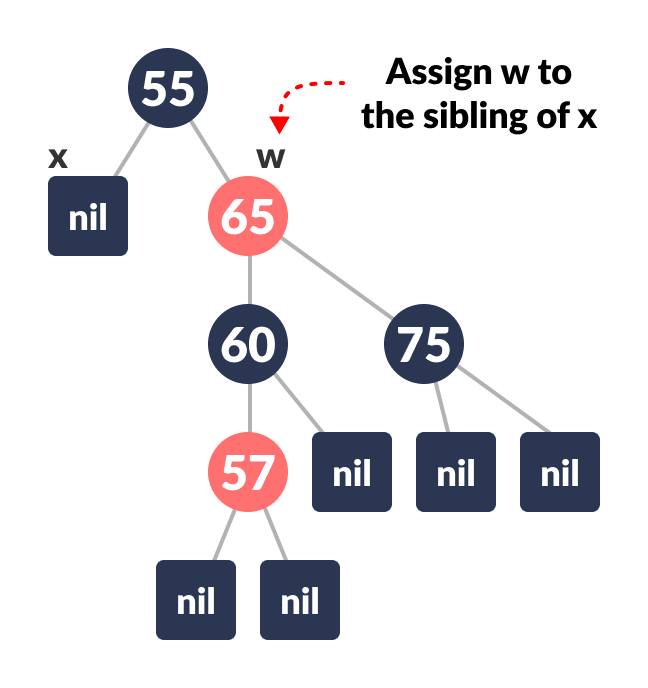

      Assigning w

    2. If the sibling of x is RED,
      Case-I:

      1. Set the color of the right child of the parent of x as BLACK.

      2. Set the color of the parent of x as RED.

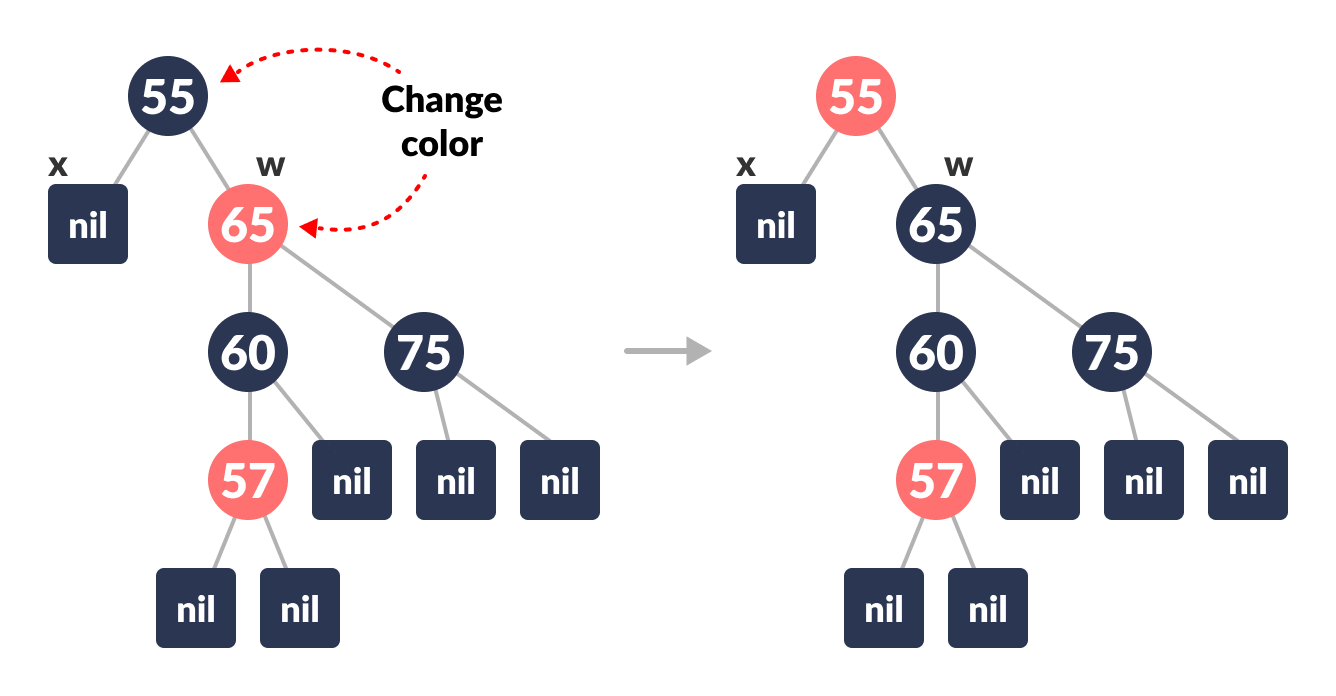
        Color change

      3. Left-Rotate the parent of x.

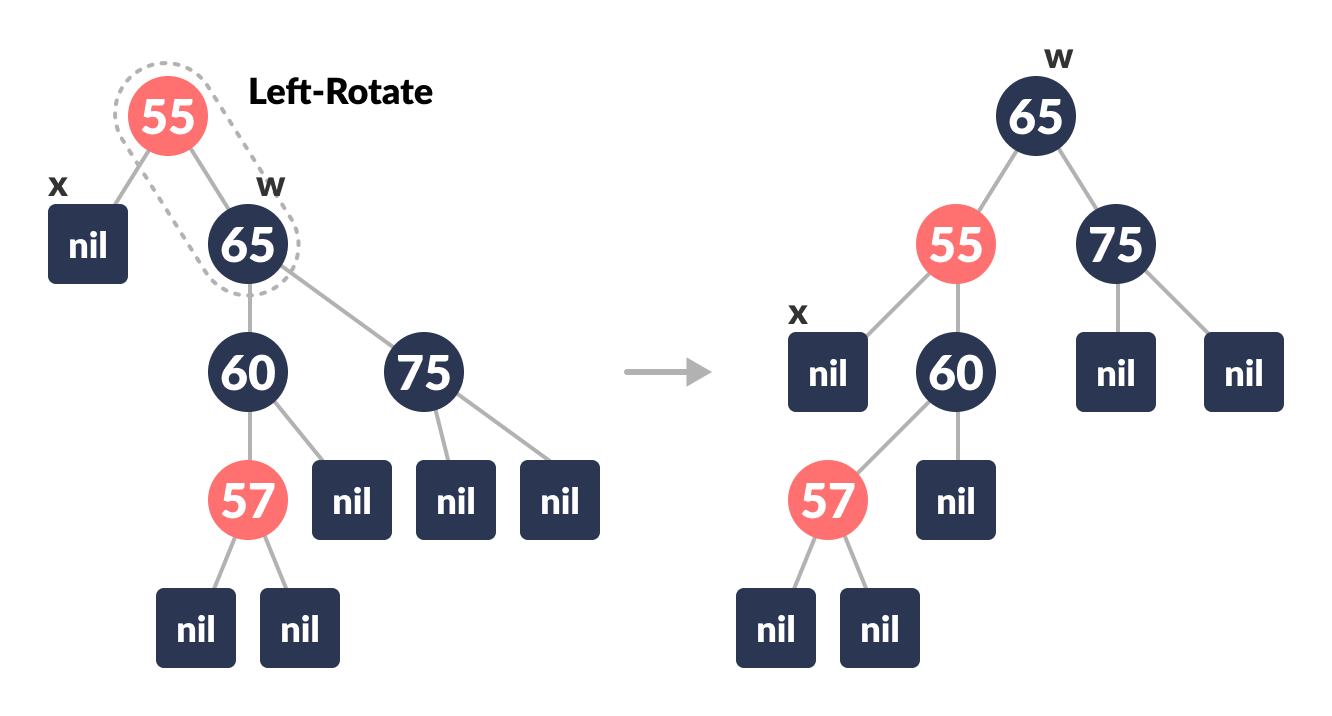
        Left-rotate

      4. Assign the rightChild of the parent of x to w.

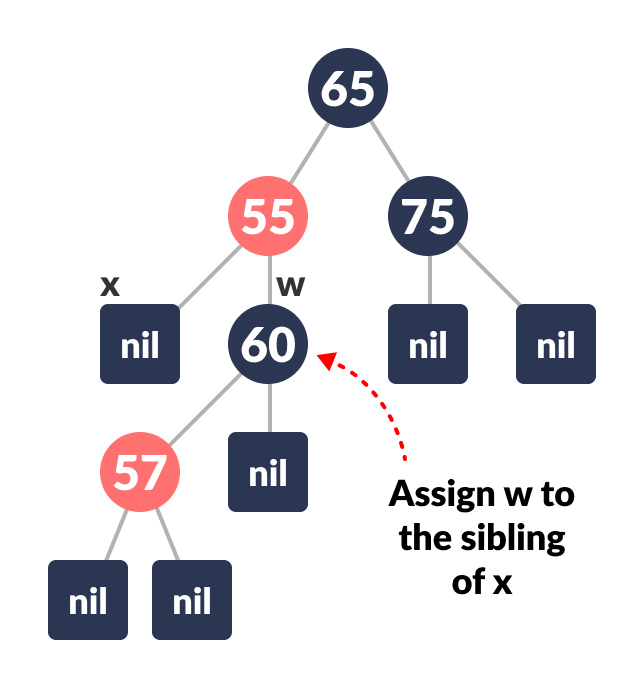
        Reassign w

    3. If the color of both the right and the leftChild of w is BLACK,
      Case-II:

      1. Set the color of w as RED
      2. Assign the parent of x to x.

    4. Else if the color of the rightChild of w is BLACK
      Case-III:

      1. Set the color of the leftChild of w as BLACK

      2. Set the color of w as RED

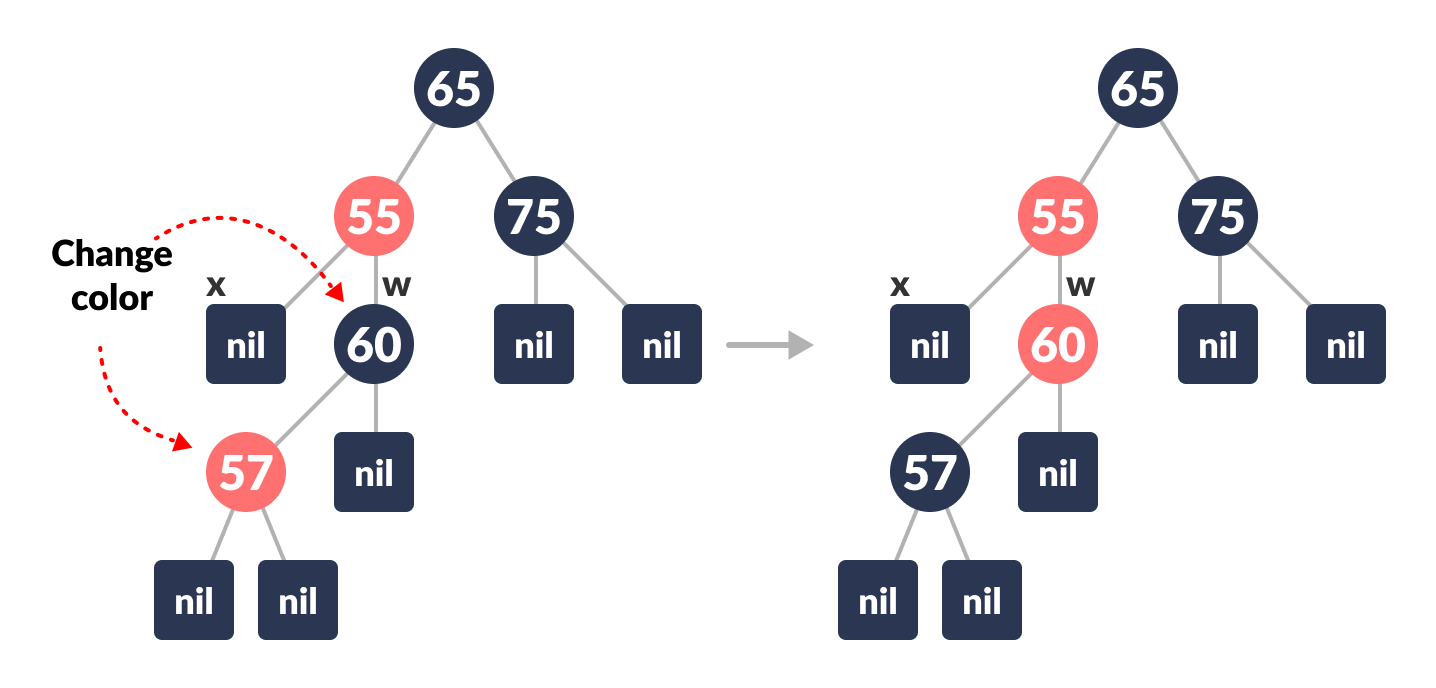
        Color change

      3. Right-Rotate w.

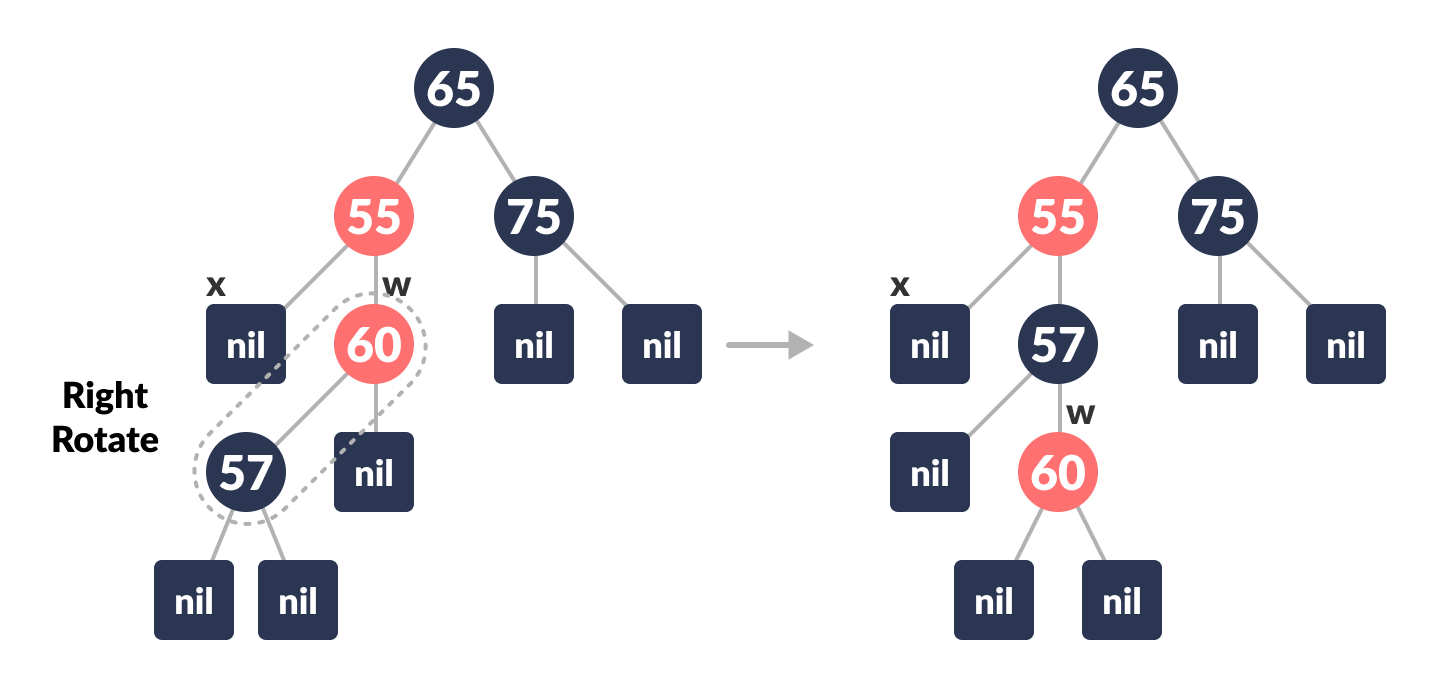
        Right rotate

      4. Assign the rightChild of the parent of x to w.

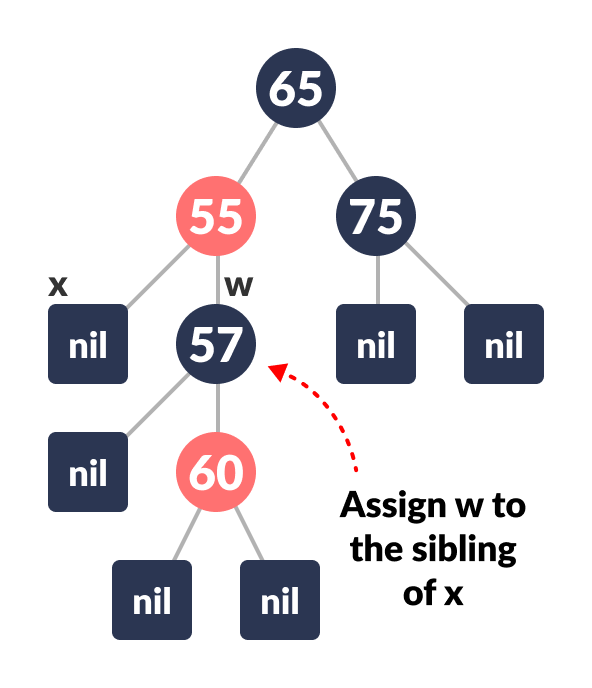
        Reassign w

    5. If any of the above cases do not occur, then do the following.
      Case-IV:

      1. Set the color of w as the color of the parent of x.

      2. Set the color of the parent of parent of x as BLACK.

      3. Set the color of the right child of w as BLACK.

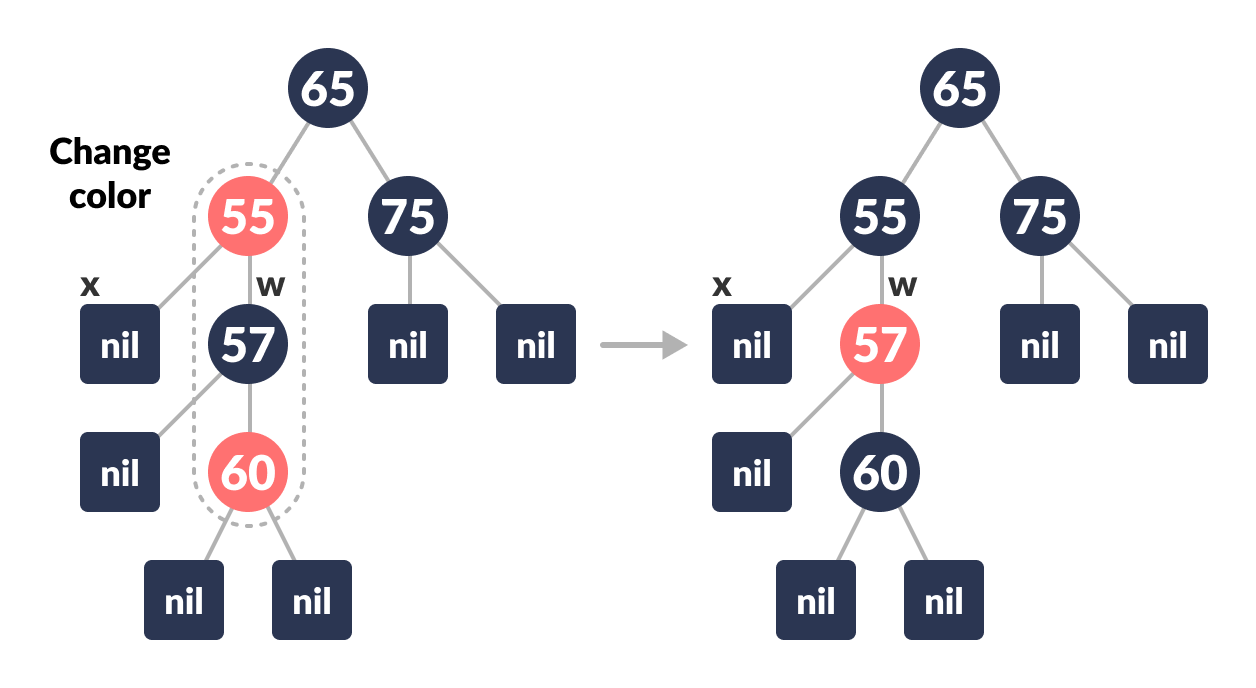
        Color change

      4. Left-Rotate the parent of x.

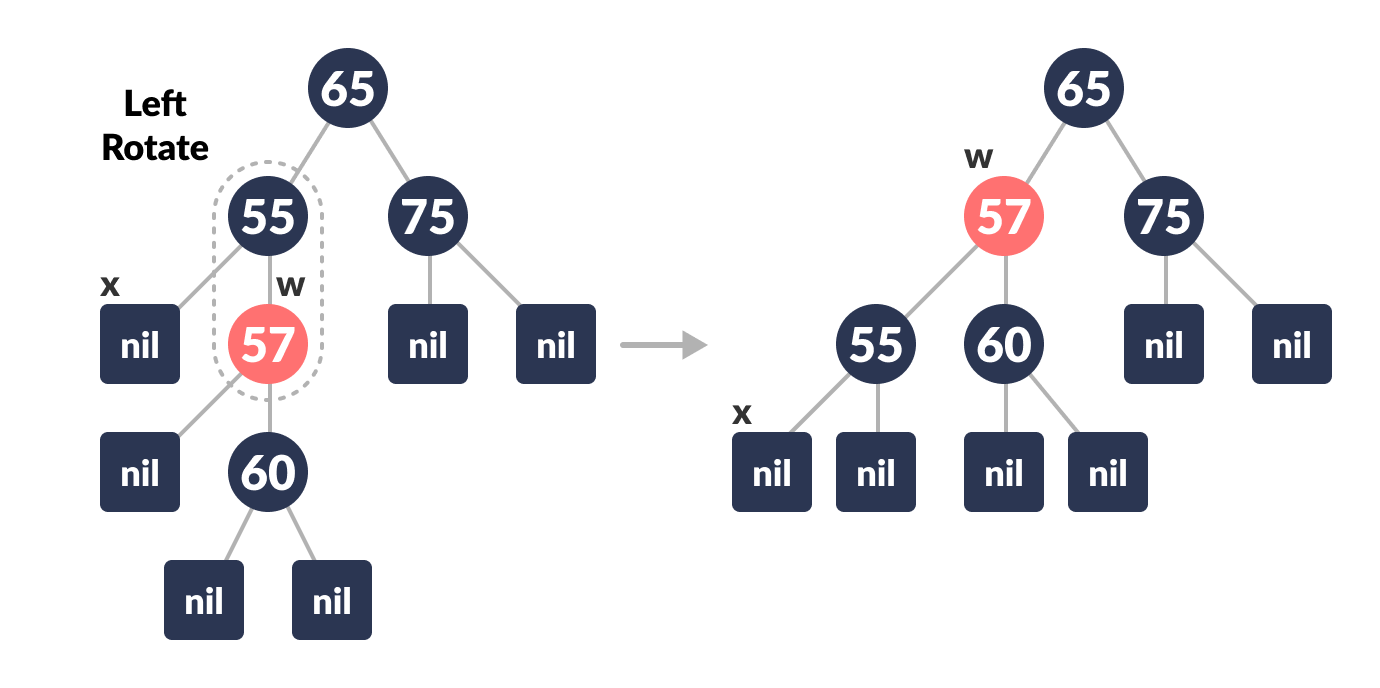
        Left-rotate

      5. Set x as the root of the tree.

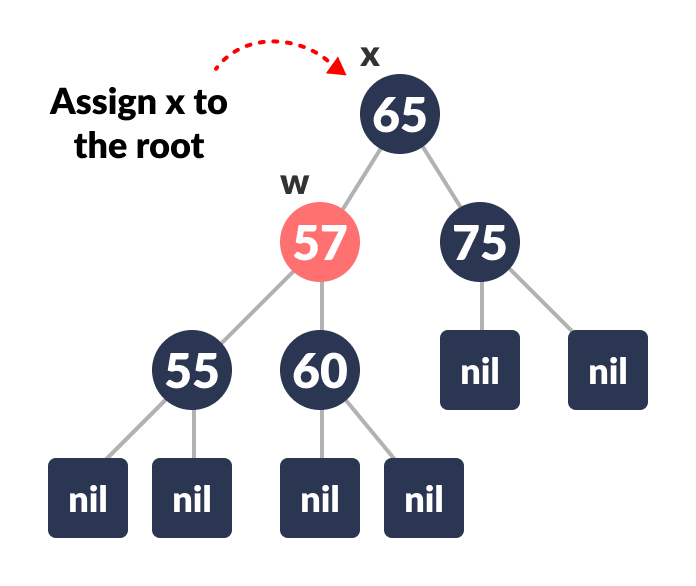
        Set x as root

  3. Else same as above with right changed to left and vice versa.
  4. Set the color of x as BLACK.

The workflow of the above cases can be understood with the help of the flowchart below.

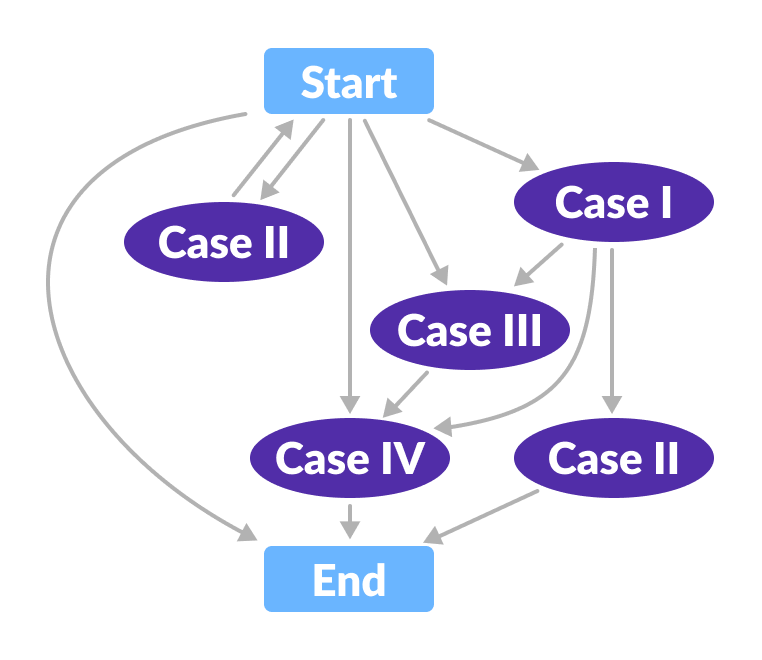
Flowchart for deletion operation

Implementation

Python

# Implementing Red-Black Tree in Python
 
 
import sys
 
 
# Node creation
class Node ():
    def __init__(self, item):
        self. item = item
        self. parent = None
        self. left = None
        self. right = None
        self. color = 1
 
 
class RedBlackTree ():
    def __init__(self):
        self. TNULL = Node (0)
        self. TNULL. color = 0
        self. TNULL. left = None
        self. TNULL. right = None
        self. root = self. TNULL
 
    # Preorder
    def pre_order_helper (self, node):
        if node != TNULL:
            sys.stdout.write (node. item + " ")
            self. pre_order_helper (node. left)
            self. pre_order_helper (node. right)
 
    # Inorder
    def in_order_helper (self, node):
        if node != TNULL:
            self. in_order_helper (node. left)
            sys.stdout.write (node. item + " ")
            self. in_order_helper (node. right)
 
    # Postorder
    def post_order_helper (self, node):
        if node != TNULL:
            self. post_order_helper (node. left)
            self. post_order_helper (node. right)
            sys.stdout.write (node. item + " ")
 
    # Search the tree
    def search_tree_helper (self, node, key):
        if node == TNULL or key == node. item:
            return node
 
        if key < node. item:
            return self. search_tree_helper (node. left, key)
        return self. search_tree_helper (node. right, key)
 
    # Balancing the tree after deletion
    def delete_fix (self, x):
        while x != self. root and x.color == 0:
            if x == x.parent. left:
                s = x.parent. right
                if s.color == 1:
                    s.color = 0
                    x.parent. color = 1
                    self. left_rotate (x.parent)
                    s = x.parent. right
 
                if s.left. color == 0 and s.right. color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.right. color == 0:
                        s.left. color = 0
                        s.color = 1
                        self. right_rotate (s)
                        s = x.parent. right
 
                    s.color = x.parent. color
                    x.parent. color = 0
                    s.right. color = 0
                    self. left_rotate (x.parent)
                    x = self. root
            else:
                s = x.parent. left
                if s.color == 1:
                    s.color = 0
                    x.parent. color = 1
                    self. right_rotate (x.parent)
                    s = x.parent. left
 
                if s.right. color == 0 and s.right. color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.left. color == 0:
                        s.right. color = 0
                        s.color = 1
                        self. left_rotate (s)
                        s = x.parent. left
 
                    s.color = x.parent. color
                    x.parent. color = 0
                    s.left. color = 0
                    self. right_rotate (x.parent)
                    x = self. root
        x.color = 0
 
    def __rb_transplant (self, u, v):
        if u.parent == None:
            self. root = v
        elif u == u.parent. left:
            u.parent. left = v
        else:
            u.parent. right = v
        v.parent = u.parent
 
    # Node deletion
    def delete_node_helper (self, node, key):
        `z` = self. TNULL
        while node != self. TNULL:
            if node. item == key:
                `z` = node
 
            if node. item <= key:
                node = node. right
            else:
                node = node. left
 
        if `z` == self. TNULL:
            print ("Cannot find key in the tree")
            return
 
        y = `z`
        y_original_color = y.color
        if `z`.left == self. TNULL:
            x = `z`.right
            self.__rb_transplant (`z`, `z`.right)
        elif (`z`.right == self. TNULL):
            x = `z`.left
            self.__rb_transplant (`z`, `z`.left)
        else:
            y = self.minimum (`z`.right)
            y_original_color = y.color
            x = y.right
            if y.parent == `z`:
                x.parent = y
            else:
                self.__rb_transplant (y, y.right)
                y.right = `z`.right
                y.right. parent = y
 
            self.__rb_transplant (`z`, y)
            y.left = `z`.left
            y.left. parent = y
            y.color = `z`.color
        if y_original_color == 0:
            self. delete_fix (x)
 
    # Balance the tree after insertion
    def fix_insert (self, k):
        while k.parent. color == 1:
            if k.parent == k.parent. parent. right:
                u = k.parent. parent. left
                if u.color == 1:
                    u.color = 0
                    k.parent. color = 0
                    k.parent. parent. color = 1
                    k = k.parent. parent
                else:
                    if k == k.parent. left:
                        k = k.parent
                        self. right_rotate (k)
                    k.parent. color = 0
                    k.parent. parent. color = 1
                    self. left_rotate (k.parent. parent)
            else:
                u = k.parent. parent. right
 
                if u.color == 1:
                    u.color = 0
                    k.parent. color = 0
                    k.parent. parent. color = 1
                    k = k.parent. parent
                else:
                    if k == k.parent. right:
                        k = k.parent
                        self. left_rotate (k)
                    k.parent. color = 0
                    k.parent. parent. color = 1
                    self. right_rotate (k.parent. parent)
            if k == self. root:
                break
        self. root. color = 0
 
    # Printing the tree
    def __print_helper (self, node, indent, last):
        if node != self. TNULL:
            sys.stdout.write (indent)
            if last:
                sys.stdout.write ("R----")
                indent += "     "
            else:
                sys.stdout.write ("L----")
                indent += "|    "
 
            s_color = "RED" if node. color == 1 else "BLACK"
            print (str (node. item) + " (" + s_color + ")")
            self.__print_helper (node. left, indent, False)
            self.__print_helper (node. right, indent, True)
 
    def preorder (self):
        self. pre_order_helper (self. root)
 
    def inorder (self):
        self. in_order_helper (self. root)
 
    def postorder (self):
        self. post_order_helper (self. root)
 
    def searchTree (self, k):
        return self. search_tree_helper (self. root, k)
 
    def minimum (self, node):
        while node. left != self. TNULL:
            node = node. left
        return node
 
    def maximum (self, node):
        while node. right != self. TNULL:
            node = node. right
        return node
 
    def successor (self, x):
        if x.right != self. TNULL:
            return self.minimum (x.right)
 
        y = x.parent
        while y != self. TNULL and x == y.right:
            x = y
            y = y.parent
        return y
 
    def predecessor (self,  x):
        if (x.left != self. TNULL):
            return self.maximum (x.left)
 
        y = x.parent
        while y != self. TNULL and x == y.left:
            x = y
            y = y.parent
 
        return y
 
    def left_rotate (self, x):
        y = x.right
        x.right = y.left
        if y.left != self. TNULL:
            y.left. parent = x
 
        y.parent = x.parent
        if x.parent == None:
            self. root = y
        elif x == x.parent. left:
            x.parent. left = y
        else:
            x.parent. right = y
        y.left = x
        x.parent = y
 
    def right_rotate (self, x):
        y = x.left
        x.left = y.right
        if y.right != self. TNULL:
            y.right. parent = x
 
        y.parent = x.parent
        if x.parent == None:
            self. root = y
        elif x == x.parent. right:
            x.parent. right = y
        else:
            x.parent. left = y
        y.right = x
        x.parent = y
 
    def insert (self, key):
        node = Node (key)
        node. parent = None
        node. item = key
        node. left = self. TNULL
        node. right = self. TNULL
        node. color = 1
 
        y = None
        x = self. root
 
        while x != self. TNULL:
            y = x
            if node. item < x.item:
                x = x.left
            else:
                x = x.right
 
        node. parent = y
        if y == None:
            self. root = node
        elif node. item < y.item:
            y.left = node
        else:
            y.right = node
 
        if node. parent == None:
            node. color = 0
            return
 
        if node. parent. parent == None:
            return
 
        self. fix_insert (node)
 
    def get_root (self):
        return self. root
 
    def delete_node (self, item):
        self. delete_node_helper (self. root, item)
 
    def print_tree (self):
        self.__print_helper (self. root, "", True)
 
 
if __name__ == "__main__":
    bst = RedBlackTree ()
 
    bst.insert (55)
    bst.insert (40)
    bst.insert (65)
    bst.insert (60)
    bst.insert (75)
    bst.insert (57)
 
    bst. print_tree ()
 
    print ("\nAfter deleting an element")
    bst. delete_node (40)
    bst. print_tree ()

Java

// Implementing Red-Black Tree in Java
 
class Node {
  int data;
  Node parent;
  Node left;
  Node right;
  int color;
}
 
public class RedBlackTree {
  private Node root;
  private Node TNULL;
 
  // Preorder
  private void preOrderHelper (Node node) {
    if (node != TNULL) {
      System.out.print (node. data + " ");
      preOrderHelper (node. left);
      preOrderHelper (node. right);
    }
  }
 
  // Inorder
  private void inOrderHelper (Node node) {
    if (node != TNULL) {
      inOrderHelper (node. left);
      System.out.print (node. data + " ");
      inOrderHelper (node. right);
    }
  }
 
  // Post order
  private void postOrderHelper (Node node) {
    if (node != TNULL) {
      postOrderHelper (node. left);
      postOrderHelper (node. right);
      System.out.print (node. data + " ");
    }
  }
 
  // Search the tree
  private Node searchTreeHelper (Node node, int key) {
    if (node == TNULL || key == node. data) {
      return node;
    }
 
    if (key < node. data) {
      return searchTreeHelper (node. left, key);
    }
    return searchTreeHelper (node. right, key);
  }
 
  // Balance the tree after deletion of a node
  private void fixDelete (Node x) {
    Node s;
    while (x != root && x.color == 0) {
      if (x == x.parent. left) {
        s = x.parent. right;
        if (s.color == 1) {
          s.color = 0;
          x.parent. color = 1;
          leftRotate (x.parent);
          s = x.parent. right;
        }
 
        if (s.left. color == 0 && s.right. color == 0) {
          s.color = 1;
          x = x.parent;
        } else {
          if (s.right. color == 0) {
            s.left. color = 0;
            s.color = 1;
            rightRotate (s);
            s = x.parent. right;
          }
 
          s.color = x.parent. color;
          x.parent. color = 0;
          s.right. color = 0;
          leftRotate (x.parent);
          x = root;
        }
      } else {
        s = x.parent. left;
        if (s.color == 1) {
          s.color = 0;
          x.parent. color = 1;
          rightRotate (x.parent);
          s = x.parent. left;
        }
 
        if (s.right. color == 0 && s.right. color == 0) {
          s.color = 1;
          x = x.parent;
        } else {
          if (s.left. color == 0) {
            s.right. color = 0;
            s.color = 1;
            leftRotate (s);
            s = x.parent. left;
          }
 
          s.color = x.parent. color;
          x.parent. color = 0;
          s.left. color = 0;
          rightRotate (x.parent);
          x = root;
        }
      }
    }
    x.color = 0;
  }
 
  private void rbTransplant (Node u, Node v) {
    if (u.parent == null) {
      root = v;
    } else if (u == u.parent. left) {
      u.parent. left = v;
    } else {
      u.parent. right = v;
    }
    v.parent = u.parent;
  }
 
  private void deleteNodeHelper (Node node, int key) {
    Node `z` = TNULL;
    Node x, y;
    while (node != TNULL) {
      if (node. data == key) {
        `z` = node;
      }
 
      if (node. data <= key) {
        node = node. right;
      } else {
        node = node. left;
      }
    }
 
    if (`z` == TNULL) {
      System.out.println ("Couldn't find key in the tree");
      return;
    }
 
    y = `z`;
    int yOriginalColor = y.color;
    if (`z`.left == TNULL) {
      x = `z`.right;
      rbTransplant (`z`, `z`.right);
    } else if (`z`.right == TNULL) {
      x = `z`.left;
      rbTransplant (`z`, `z`.left);
    } else {
      y = minimum (`z`.right);
      yOriginalColor = y.color;
      x = y.right;
      if (y.parent == `z`) {
        x.parent = y;
      } else {
        rbTransplant (y, y.right);
        y.right = `z`.right;
        y.right. parent = y;
      }
 
      rbTransplant (`z`, y);
      y.left = `z`.left;
      y.left. parent = y;
      y.color = `z`.color;
    }
    if (yOriginalColor == 0) {
      fixDelete (x);
    }
  }
 
  // Balance the node after insertion
  private void fixInsert (Node k) {
    Node u;
    while (k.parent. color == 1) {
      if (k.parent == k.parent. parent. right) {
        u = k.parent. parent. left;
        if (u.color == 1) {
          u.color = 0;
          k.parent. color = 0;
          k.parent. parent. color = 1;
          k = k.parent. parent;
        } else {
          if (k == k.parent. left) {
            k = k.parent;
            rightRotate (k);
          }
          k.parent. color = 0;
          k.parent. parent. color = 1;
          leftRotate (k.parent. parent);
        }
      } else {
        u = k.parent. parent. right;
 
        if (u.color == 1) {
          u.color = 0;
          k.parent. color = 0;
          k.parent. parent. color = 1;
          k = k.parent. parent;
        } else {
          if (k == k.parent. right) {
            k = k.parent;
            leftRotate (k);
          }
          k.parent. color = 0;
          k.parent. parent. color = 1;
          rightRotate (k.parent. parent);
        }
      }
      if (k == root) {
        break;
      }
    }
    root. color = 0;
  }
 
  private void printHelper (Node root, String indent, boolean last) {
    if (root != TNULL) {
      System.out.print (indent);
      if (last) {
        System.out.print ("R----");
        indent += "   ";
      } else {
        System.out.print ("L----");
        indent += "|  ";
      }
 
      String sColor = root. color == 1 ? "RED" : "BLACK";
      System.out.println (root. data + " (" + sColor + ")");
      printHelper (root. left, indent, false);
      printHelper (root. right, indent, true);
    }
  }
 
  public RedBlackTree () {
    TNULL = new Node ();
    TNULL. color = 0;
    TNULL. left = null;
    TNULL. right = null;
    root = TNULL;
  }
 
  public void preorder () {
    preOrderHelper (this. root);
  }
 
  public void inorder () {
    inOrderHelper (this. root);
  }
 
  public void postorder () {
    postOrderHelper (this. root);
  }
 
  public Node searchTree (int k) {
    return searchTreeHelper (this. root, k);
  }
 
  public Node minimum (Node node) {
    while (node. left != TNULL) {
      node = node. left;
    }
    return node;
  }
 
  public Node maximum (Node node) {
    while (node. right != TNULL) {
      node = node. right;
    }
    return node;
  }
 
  public Node successor (Node x) {
    if (x.right != TNULL) {
      return minimum (x.right);
    }
 
    Node y = x.parent;
    while (y != TNULL && x == y.right) {
      x = y;
      y = y.parent;
    }
    return y;
  }
 
  public Node predecessor (Node x) {
    if (x.left != TNULL) {
      return maximum (x.left);
    }
 
    Node y = x.parent;
    while (y != TNULL && x == y.left) {
      x = y;
      y = y.parent;
    }
 
    return y;
  }
 
  public void leftRotate (Node x) {
    Node y = x.right;
    x.right = y.left;
    if (y.left != TNULL) {
      y.left. parent = x;
    }
    y.parent = x.parent;
    if (x.parent == null) {
      this. root = y;
    } else if (x == x.parent. left) {
      x.parent. left = y;
    } else {
      x.parent. right = y;
    }
    y.left = x;
    x.parent = y;
  }
 
  public void rightRotate (Node x) {
    Node y = x.left;
    x.left = y.right;
    if (y.right != TNULL) {
      y.right. parent = x;
    }
    y.parent = x.parent;
    if (x.parent == null) {
      this. root = y;
    } else if (x == x.parent. right) {
      x.parent. right = y;
    } else {
      x.parent. left = y;
    }
    y.right = x;
    x.parent = y;
  }
 
  public void insert (int key) {
    Node node = new Node ();
    node. parent = null;
    node. data = key;
    node. left = TNULL;
    node. right = TNULL;
    node. color = 1;
 
    Node y = null;
    Node x = this. root;
 
    while (x != TNULL) {
      y = x;
      if (node. data < x.data) {
        x = x.left;
      } else {
        x = x.right;
      }
    }
 
    node. parent = y;
    if (y == null) {
      root = node;
    } else if (node. data < y.data) {
      y.left = node;
    } else {
      y.right = node;
    }
 
    if (node. parent == null) {
      node. color = 0;
      return;
    }
 
    if (node. parent. parent == null) {
      return;
    }
 
    fixInsert (node);
  }
 
  public Node getRoot () {
    return this. root;
  }
 
  public void deleteNode (int data) {
    deleteNodeHelper (this. root, data);
  }
 
  public void printTree () {
    printHelper (this. root, "", true);
  }
 
  public static void main (String[] args) {
    RedBlackTree bst = new RedBlackTree ();
    bst.insert (55);
    bst.insert (40);
    bst.insert (65);
    bst.insert (60);
    bst.insert (75);
    bst.insert (57);
    bst.printTree ();
 
    System.out.println ("\nAfter deleting: ");
    bst.deleteNode (40);
    bst.printTree ();
  }
}

C

// Implementing Red-Black Tree in C
 
#include <stdio.h>
#include <stdlib.h>
 
enum nodeColor {
  RED,
  BLACK
};
 
struct rbNode {
  int data, color;
  struct rbNode *link[2];
};
 
struct rbNode *root = NULL;
 
// Create a red-black tree
struct rbNode *createNode (int data) {
  struct rbNode *newnode;
  newnode = (struct rbNode *) malloc (si`z`eof (struct rbNode));
  newnode->data = data;
  newnode->color = RED;
  newnode->link[0] = newnode->link[1] = NULL;
  return newnode;
}
 
// Insert an node
void insertion (int data) {
  struct rbNode *stack[98], *ptr, *newnode, *xPtr, *yPtr;
  int dir[98], ht = 0, index;
  ptr = root;
  if (! root) {
    root = createNode (data);
    return;
  }
 
  stack[ht] = root;
  dir[ht++] = 0;
  while (ptr != NULL) {
    if (ptr->data == data) {
      printf ("Duplicates Not Allowed!!\n");
      return;
    }
    index = (data - ptr->data) > 0 ? 1 : 0;
    stack[ht] = ptr;
    ptr = ptr->link[index];
    dir[ht++] = index;
  }
  stack[ht - 1]->link[index] = newnode = createNode (data);
  while ((ht >= 3) && (stack[ht - 1]->color == RED)) {
    if (dir[ht - 2] == 0) {
      yPtr = stack[ht - 2]->link[1];
      if (yPtr != NULL && yPtr->color == RED) {
        stack[ht - 2]->color = RED;
        stack[ht - 1]->color = yPtr->color = BLACK;
        ht = ht - 2;
      } else {
        if (dir[ht - 1] == 0) {
          yPtr = stack[ht - 1];
        } else {
          xPtr = stack[ht - 1];
          yPtr = xPtr->link[1];
          xPtr->link[1] = yPtr->link[0];
          yPtr->link[0] = xPtr;
          stack[ht - 2]->link[0] = yPtr;
        }
        xPtr = stack[ht - 2];
        xPtr->color = RED;
        yPtr->color = BLACK;
        xPtr->link[0] = yPtr->link[1];
        yPtr->link[1] = xPtr;
        if (xPtr == root) {
          root = yPtr;
        } else {
          stack[ht - 3]->link[dir[ht - 3]] = yPtr;
        }
        break;
      }
    } else {
      yPtr = stack[ht - 2]->link[0];
      if ((yPtr != NULL) && (yPtr->color == RED)) {
        stack[ht - 2]->color = RED;
        stack[ht - 1]->color = yPtr->color = BLACK;
        ht = ht - 2;
      } else {
        if (dir[ht - 1] == 1) {
          yPtr = stack[ht - 1];
        } else {
          xPtr = stack[ht - 1];
          yPtr = xPtr->link[0];
          xPtr->link[0] = yPtr->link[1];
          yPtr->link[1] = xPtr;
          stack[ht - 2]->link[1] = yPtr;
        }
        xPtr = stack[ht - 2];
        yPtr->color = BLACK;
        xPtr->color = RED;
        xPtr->link[1] = yPtr->link[0];
        yPtr->link[0] = xPtr;
        if (xPtr == root) {
          root = yPtr;
        } else {
          stack[ht - 3]->link[dir[ht - 3]] = yPtr;
        }
        break;
      }
    }
  }
  root->color = BLACK;
}
 
// Delete a node
void deletion (int data) {
  struct rbNode *stack[98], *ptr, *xPtr, *yPtr;
  struct rbNode *pPtr, *qPtr, *rPtr;
  int dir[98], ht = 0, diff, i;
  enum nodeColor color;
 
  if (! root) {
    printf ("Tree not available\n");
    return;
  }
 
  ptr = root;
  while (ptr != NULL) {
    if ((data - ptr->data) == 0)
      break;
    diff = (data - ptr->data) > 0 ? 1 : 0;
    stack[ht] = ptr;
    dir[ht++] = diff;
    ptr = ptr->link[diff];
  }
 
  if (ptr->link[1] == NULL) {
    if ((ptr == root) && (ptr->link[0] == NULL)) {
      free (ptr);
      root = NULL;
    } else if (ptr == root) {
      root = ptr->link[0];
      free (ptr);
    } else {
      stack[ht - 1]->link[dir[ht - 1]] = ptr->link[0];
    }
  } else {
    xPtr = ptr->link[1];
    if (xPtr->link[0] == NULL) {
      xPtr->link[0] = ptr->link[0];
      color = xPtr->color;
      xPtr->color = ptr->color;
      ptr->color = color;
 
      if (ptr == root) {
        root = xPtr;
      } else {
        stack[ht - 1]->link[dir[ht - 1]] = xPtr;
      }
 
      dir[ht] = 1;
      stack[ht++] = xPtr;
    } else {
      i = ht++;
      while (1) {
        dir[ht] = 0;
        stack[ht++] = xPtr;
        yPtr = xPtr->link[0];
        if (! yPtr->link[0])
          break;
        xPtr = yPtr;
      }
 
      dir[i] = 1;
      stack[i] = yPtr;
      if (i > 0)
        stack[i - 1]->link[dir[i - 1]] = yPtr;
 
      yPtr->link[0] = ptr->link[0];
 
      xPtr->link[0] = yPtr->link[1];
      yPtr->link[1] = ptr->link[1];
 
      if (ptr == root) {
        root = yPtr;
      }
 
      color = yPtr->color;
      yPtr->color = ptr->color;
      ptr->color = color;
    }
  }
 
  if (ht < 1)
    return;
 
  if (ptr->color == BLACK) {
    while (1) {
      pPtr = stack[ht - 1]->link[dir[ht - 1]];
      if (pPtr && pPtr->color == RED) {
        pPtr->color = BLACK;
        break;
      }
 
      if (ht < 2)
        break;
 
      if (dir[ht - 2] == 0) {
        rPtr = stack[ht - 1]->link[1];
 
        if (! rPtr)
          break;
 
        if (rPtr->color == RED) {
          stack[ht - 1]->color = RED;
          rPtr->color = BLACK;
          stack[ht - 1]->link[1] = rPtr->link[0];
          rPtr->link[0] = stack[ht - 1];
 
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          dir[ht] = 0;
          stack[ht] = stack[ht - 1];
          stack[ht - 1] = rPtr;
          ht++;
 
          rPtr = stack[ht - 1]->link[1];
        }
 
        if ((! rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
          (! rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
          rPtr->color = RED;
        } else {
          if (! rPtr->link[1] || rPtr->link[1]->color == BLACK) {
            qPtr = rPtr->link[0];
            rPtr->color = RED;
            qPtr->color = BLACK;
            rPtr->link[0] = qPtr->link[1];
            qPtr->link[1] = rPtr;
            rPtr = stack[ht - 1]->link[1] = qPtr;
          }
          rPtr->color = stack[ht - 1]->color;
          stack[ht - 1]->color = BLACK;
          rPtr->link[1]->color = BLACK;
          stack[ht - 1]->link[1] = rPtr->link[0];
          rPtr->link[0] = stack[ht - 1];
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          break;
        }
      } else {
        rPtr = stack[ht - 1]->link[0];
        if (! rPtr)
          break;
 
        if (rPtr->color == RED) {
          stack[ht - 1]->color = RED;
          rPtr->color = BLACK;
          stack[ht - 1]->link[0] = rPtr->link[1];
          rPtr->link[1] = stack[ht - 1];
 
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          dir[ht] = 1;
          stack[ht] = stack[ht - 1];
          stack[ht - 1] = rPtr;
          ht++;
 
          rPtr = stack[ht - 1]->link[0];
        }
        if ((! rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
          (! rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
          rPtr->color = RED;
        } else {
          if (! rPtr->link[0] || rPtr->link[0]->color == BLACK) {
            qPtr = rPtr->link[1];
            rPtr->color = RED;
            qPtr->color = BLACK;
            rPtr->link[1] = qPtr->link[0];
            qPtr->link[0] = rPtr;
            rPtr = stack[ht - 1]->link[0] = qPtr;
          }
          rPtr->color = stack[ht - 1]->color;
          stack[ht - 1]->color = BLACK;
          rPtr->link[0]->color = BLACK;
          stack[ht - 1]->link[0] = rPtr->link[1];
          rPtr->link[1] = stack[ht - 1];
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          break;
        }
      }
      ht--;
    }
  }
}
 
// Print the inorder traversal of the tree
void inorderTraversal (struct rbNode *node) {
  if (node) {
    inorderTraversal (node->link[0]);
    printf ("%d  ", node->data);
    inorderTraversal (node->link[1]);
  }
  return;
}
 
// Driver code
int main () {
  int ch, data;
  while (1) {
    printf ("1. Insertion\t2. Deletion\n");
    printf ("3. Traverse\t4. Exit");
    printf ("\nEnter your choice: ");
    scanf ("%d", &ch);
    switch (ch) {
      case 1:
        printf ("Enter the element to insert: ");
        scanf ("%d", &data);
        insertion (data);
        break;
      case 2:
        printf ("Enter the element to delete: ");
        scanf ("%d", &data);
        deletion (data);
        break;
      case 3:
        inorderTraversal (root);
        printf ("\n");
        break;
      case 4:
        exit (0);
      default:
        printf ("Not available\n");
        break;
    }
    printf ("\n");
  }
  return 0;
}

Cpp

// Implementing Red-Black Tree in C++
 
#include <iostream>
using namespace std;
 
struct Node {
  int data;
  Node *parent;
  Node *left;
  Node *right;
  int color;
};
 
typedef Node *NodePtr;
 
class RedBlackTree {
   private:
  NodePtr root;
  NodePtr TNULL;
 
  void initiali`z`eNULLNode (NodePtr node, NodePtr parent) {
    node->data = 0;
    node->parent = parent;
    node->left = nullptr;
    node->right = nullptr;
    node->color = 0;
  }
 
  // Preorder
  void preOrderHelper (NodePtr node) {
    if (node != TNULL) {
      cout << node->data << " ";
      preOrderHelper (node->left);
      preOrderHelper (node->right);
    }
  }
 
  // Inorder
  void inOrderHelper (NodePtr node) {
    if (node != TNULL) {
      inOrderHelper (node->left);
      cout << node->data << " ";
      inOrderHelper (node->right);
    }
  }
 
  // Post order
  void postOrderHelper (NodePtr node) {
    if (node != TNULL) {
      postOrderHelper (node->left);
      postOrderHelper (node->right);
      cout << node->data << " ";
    }
  }
 
  NodePtr searchTreeHelper (NodePtr node, int key) {
    if (node == TNULL || key == node->data) {
      return node;
    }
 
    if (key < node->data) {
      return searchTreeHelper (node->left, key);
    }
    return searchTreeHelper (node->right, key);
  }
 
  // For balancing the tree after deletion
  void deleteFix (NodePtr x) {
    NodePtr s;
    while (x != root && x->color == 0) {
      if (x == x->parent->left) {
        s = x->parent->right;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          leftRotate (x->parent);
          s = x->parent->right;
        }
 
        if (s->left->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->right->color == 0) {
            s->left->color = 0;
            s->color = 1;
            rightRotate (s);
            s = x->parent->right;
          }
 
          s->color = x->parent->color;
          x->parent->color = 0;
          s->right->color = 0;
          leftRotate (x->parent);
          x = root;
        }
      } else {
        s = x->parent->left;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          rightRotate (x->parent);
          s = x->parent->left;
        }
 
        if (s->right->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->left->color == 0) {
            s->right->color = 0;
            s->color = 1;
            leftRotate (s);
            s = x->parent->left;
          }
 
          s->color = x->parent->color;
          x->parent->color = 0;
          s->left->color = 0;
          rightRotate (x->parent);
          x = root;
        }
      }
    }
    x->color = 0;
  }
 
  void rbTransplant (NodePtr u, NodePtr v) {
    if (u->parent == nullptr) {
      root = v;
    } else if (u == u->parent->left) {
      u->parent->left = v;
    } else {
      u->parent->right = v;
    }
    v->parent = u->parent;
  }
 
  void deleteNodeHelper (NodePtr node, int key) {
    NodePtr `z` = TNULL;
    NodePtr x, y;
    while (node != TNULL) {
      if (node->data == key) {
        `z` = node;
      }
 
      if (node->data <= key) {
        node = node->right;
      } else {
        node = node->left;
      }
    }
 
    if (`z` == TNULL) {
      cout << "Key not found in the tree" << endl;
      return;
    }
 
    y = `z`;
    int y_original_color = y->color;
    if (`z`->left == TNULL) {
      x = `z`->right;
      rbTransplant (`z`, `z`->right);
    } else if (`z`->right == TNULL) {
      x = `z`->left;
      rbTransplant (`z`, `z`->left);
    } else {
      y = minimum (`z`->right);
      y_original_color = y->color;
      x = y->right;
      if (y->parent == `z`) {
        x->parent = y;
      } else {
        rbTransplant (y, y->right);
        y->right = `z`->right;
        y->right->parent = y;
      }
 
      rbTransplant (`z`, y);
      y->left = `z`->left;
      y->left->parent = y;
      y->color = `z`->color;
    }
    delete `z`;
    if (y_original_color == 0) {
      deleteFix (x);
    }
  }
 
  // For balancing the tree after insertion
  void insertFix (NodePtr k) {
    NodePtr u;
    while (k->parent->color == 1) {
      if (k->parent == k->parent->parent->right) {
        u = k->parent->parent->left;
        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->left) {
            k = k->parent;
            rightRotate (k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          leftRotate (k->parent->parent);
        }
      } else {
        u = k->parent->parent->right;
 
        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->right) {
            k = k->parent;
            leftRotate (k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          rightRotate (k->parent->parent);
        }
      }
      if (k == root) {
        break;
      }
    }
    root->color = 0;
  }
 
  void printHelper (NodePtr root, string indent, bool last) {
    if (root != TNULL) {
      cout << indent;
      if (last) {
        cout << "R----";
        indent += "   ";
      } else {
        cout << "L----";
        indent += "|  ";
      }
 
      string sColor = root->color ? "RED" : "BLACK";
      cout << root->data << " (" << sColor << ")" << endl;
      printHelper (root->left, indent, false);
      printHelper (root->right, indent, true);
    }
  }
 
   public:
  RedBlackTree () {
    TNULL = new Node;
    TNULL->color = 0;
    TNULL->left = nullptr;
    TNULL->right = nullptr;
    root = TNULL;
  }
 
  void preorder () {
    preOrderHelper (this->root);
  }
 
  void inorder () {
    inOrderHelper (this->root);
  }
 
  void postorder () {
    postOrderHelper (this->root);
  }
 
  NodePtr searchTree (int k) {
    return searchTreeHelper (this->root, k);
  }
 
  NodePtr minimum (NodePtr node) {
    while (node->left != TNULL) {
      node = node->left;
    }
    return node;
  }
 
  NodePtr maximum (NodePtr node) {
    while (node->right != TNULL) {
      node = node->right;
    }
    return node;
  }
 
  NodePtr successor (NodePtr x) {
    if (x->right != TNULL) {
      return minimum (x->right);
    }
 
    NodePtr y = x->parent;
    while (y != TNULL && x == y->right) {
      x = y;
      y = y->parent;
    }
    return y;
  }
 
  NodePtr predecessor (NodePtr x) {
    if (x->left != TNULL) {
      return maximum (x->left);
    }
 
    NodePtr y = x->parent;
    while (y != TNULL && x == y->left) {
      x = y;
      y = y->parent;
    }
 
    return y;
  }
 
  void leftRotate (NodePtr x) {
    NodePtr y = x->right;
    x->right = y->left;
    if (y->left != TNULL) {
      y->left->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->left) {
      x->parent->left = y;
    } else {
      x->parent->right = y;
    }
    y->left = x;
    x->parent = y;
  }
 
  void rightRotate (NodePtr x) {
    NodePtr y = x->left;
    x->left = y->right;
    if (y->right != TNULL) {
      y->right->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->right) {
      x->parent->right = y;
    } else {
      x->parent->left = y;
    }
    y->right = x;
    x->parent = y;
  }
 
  // Inserting a node
  void insert (int key) {
    NodePtr node = new Node;
    node->parent = nullptr;
    node->data = key;
    node->left = TNULL;
    node->right = TNULL;
    node->color = 1;
 
    NodePtr y = nullptr;
    NodePtr x = this->root;
 
    while (x != TNULL) {
      y = x;
      if (node->data < x->data) {
        x = x->left;
      } else {
        x = x->right;
      }
    }
 
    node->parent = y;
    if (y == nullptr) {
      root = node;
    } else if (node->data < y->data) {
      y->left = node;
    } else {
      y->right = node;
    }
 
    if (node->parent == nullptr) {
      node->color = 0;
      return;
    }
 
    if (node->parent->parent == nullptr) {
      return;
    }
 
    insertFix (node);
  }
 
  NodePtr getRoot () {
    return this->root;
  }
 
  void deleteNode (int data) {
    deleteNodeHelper (this->root, data);
  }
 
  void printTree () {
    if (root) {
      printHelper (this->root, "", true);
    }
  }
};
 
int main () {
  RedBlackTree bst;
  bst.insert (55);
  bst.insert (40);
  bst.insert (65);
  bst.insert (60);
  bst.insert (75);
  bst.insert (57);
 
  bst.printTree ();
  cout << endl
     << "After deleting" << endl;
  bst.deleteNode (40);
  bst.printTree ();
}

Red-Black Tree Applications

  1. To implement finite maps
  2. To implement Java packages: java.util.TreeMap and java.util.TreeSet
  3. To implement Standard Template Libraries (STL) in C++: multiset, map, multimap
  4. In Linux Kernel (CPU scheduling - CFS)

关系图谱