40-Stack_Queue

Stack ADT

栈（stack）是受限的序列
- 只能在栈顶（top）插入和删除
- 栈底（bottom）为盲端
基本接口
- size() / empty()
- push() 入栈
- pop() 出栈
- top() 查顶
后进先出（LIFO）

扩展接口：`getMax()`

使用一个辅助栈来跟踪最大元素：

维护两个栈，一个是主栈用于正常的 push 和 pop 操作，另一个是辅助栈用于跟踪最大元素。
当往主栈中压入一个元素时，首先检查辅助栈是否为空。如果为空，就将这个元素同时压入辅助栈。
如果辅助栈不为空，就比较要压入主栈的元素与辅助栈栈顶元素的大小。如果新元素大于等于栈顶元素，就将新元素压入辅助栈。否则，不将新元素压入辅助栈，保持辅助栈栈顶元素不变。
当你主栈中弹出元素时，同时也从辅助栈中弹出元素。这样，辅助栈始终反映了主栈中的最大元素。
如果你需要查找栈中的最大元素，只需查看辅助栈的栈顶元素，它将是当前主栈中的最大元素。

class MaxStack {
public:
    void push(int x) {
        // 压入主栈
        mainStack.push(x);
 
        // 检查辅助栈是否为空，或者新元素大于等于辅助栈的栈顶元素
        if (maxStack.empty() || x >= maxStack.top()) {
            maxStack.push(x);
        }
    }
 
    void pop() {
        if (!mainStack.empty()) {
            // 如果主栈的栈顶元素等于辅助栈的栈顶元素，同时从辅助栈弹出元素
            if (mainStack.top() == maxStack.top()) {
                maxStack.pop();
            }
            mainStack.pop();
        }
    }
 
    int getMax() {
        if (!maxStack.empty()) {
            return maxStack.top();
        }
        // 如果辅助栈为空，栈中没有元素，可以根据需要返回一个默认值或抛出异常
        // 这里简单地返回0，你可以根据实际需求进行更改
        return 0;
    }
 
private:
    std::stack<int> mainStack;  // 主栈用于正常的push和pop操作
    std::stack<int> maxStack;   // 辅助栈用于跟踪最大元素
};

使用 steap 结构实现

Steap

函数调用栈

原理

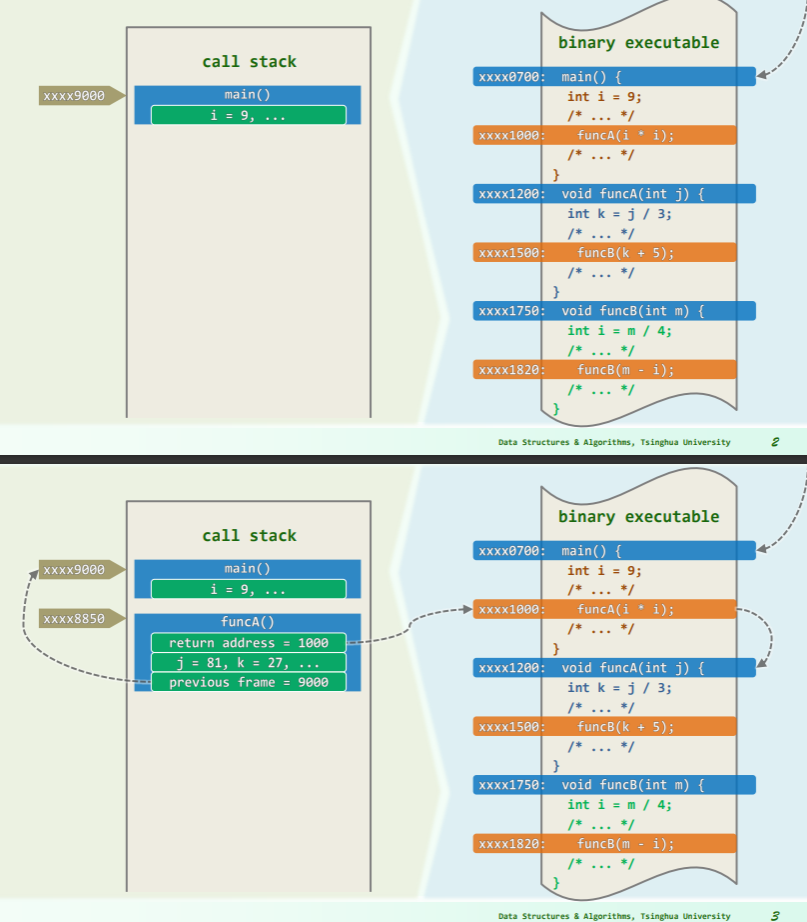
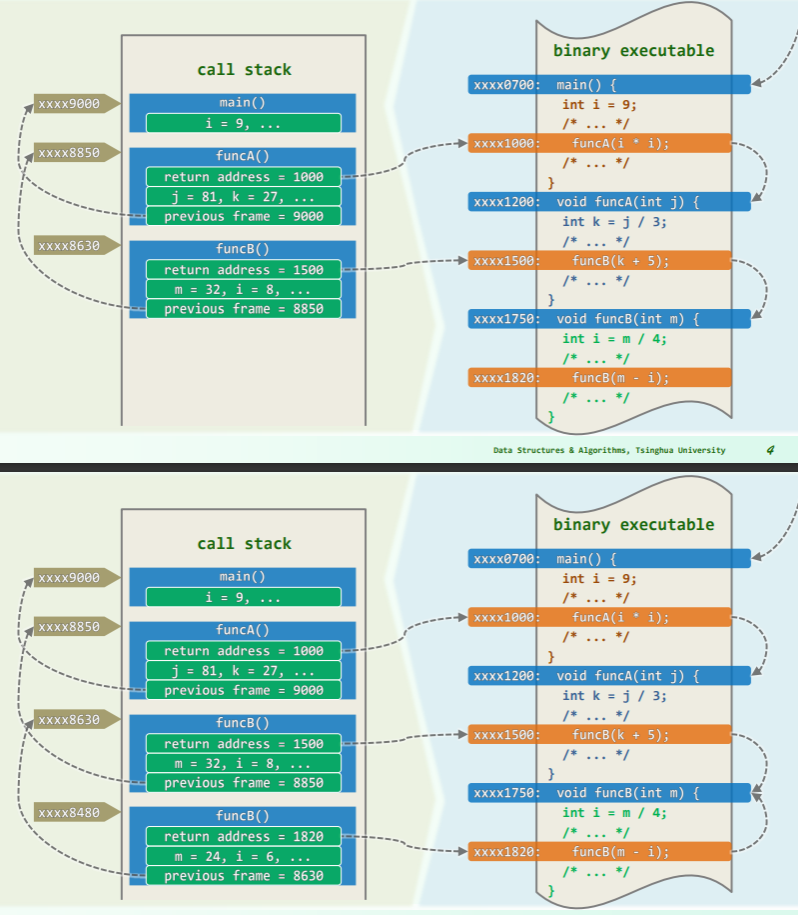
深度与空间

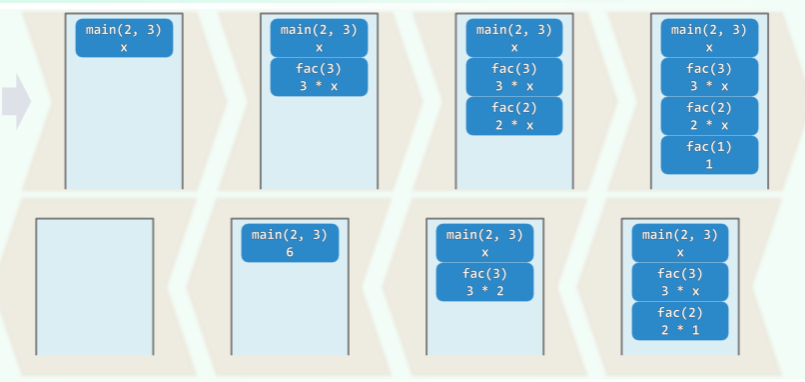
递归法求阶乘

int fac(int n){
	return (n<2) ? 1 : n * fac(n-1);
}

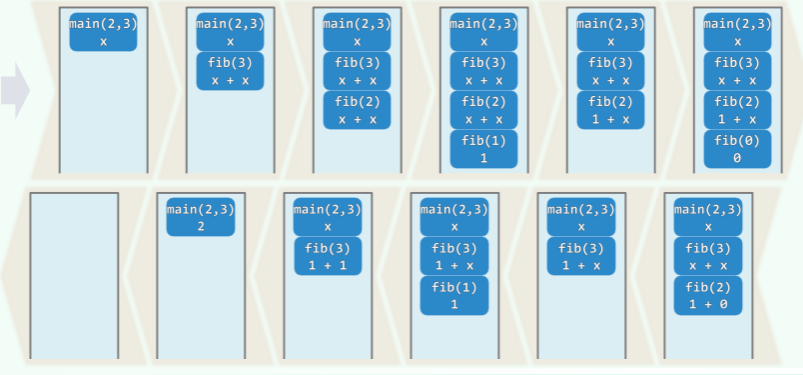
递归求 fib 序列

int fib(int n){
	return (n<2) ? n : fib(n-1) + fib(n-2);
}

空间复杂度

递归算法所需的空间，主要取决于递归深度，而非递归实例总数：

hailstone(int n) {
	if ( 1 < n )
	n % 2 ? odd( n ) : even( n );
}
even( int n ) { hailstone( n / 2 ); }
odd( int n ) { hailstone( 3*n + 1 ); }
 
main( int argc, char* argv[] )
{ hailstone( atoi( argv[1] ) ); }

消除递归

递归函数的空间复杂度

主要取决于最大递归深度
而非递归实例总数

为隐式地维护调用栈，需花费额外的时间、空间——为节省空间，可

显式地维护调用栈
将递归算法改写为迭代版本

// version: recurrence
int fac( int n ) {
	int f = 1; //O(1)空间
	while ( n > 1 )
		f *= n--;
	return f;
}
 
int fib( int n ) { //O(1)空间
	int f = 0, g = 1;
	while ( 0 < n-- )
		{ g += f; f = g - f; }
	return f;
}
 
void hailstone( int n ) { //O(1)空间
	while ( 1 < n )
		n = n % 2 ? 3*n + 1 : n/2;
}

尾递归

定义

尾递归指递归调用在函数体最后一步的递归调用。
递归求 factorial 的最后一步是乘法与函数的自我调用。

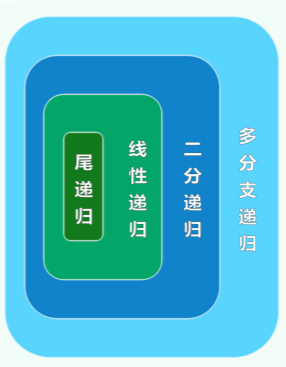
特点

尾递归是最简单的递归模式：一旦抵达递归基，便会引发一连串的 return（且返回地址相同），调用栈相应地连续 pop。

故不难改写为迭代形式，越来越多的编译器可以自动识别并代为改写

时间复杂度有常系数改进
空间复杂度或有渐近改进

消除尾递归

进制转换

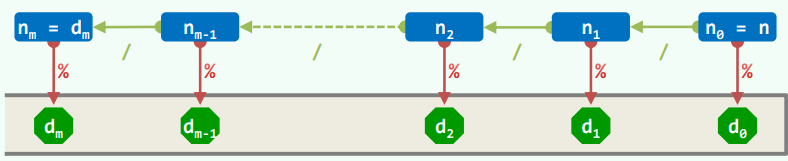
数制转换原理

$λ$ 进制的数可以表示为：

n = (d_{m} ... d_{2} d_{1} d_{0})_{λ} = d_{m} \cdot λ^{m} + ... + d_{2} \cdot λ^{2} + d_{1} \cdot λ^{1} + d_{0} \cdot λ^{0}

则令： $n_{i} = (d_{m} ... d_{i + 2} d_{i + 1} d_{i})_{λ}$

有： $n_{i + 1} = n_{i} / λ$ 和 $d_{i} = n_{i} % λ$

如此对 $λ$ 反复整除、取余，即可自低而高得出 $λ$ 进制的各位。

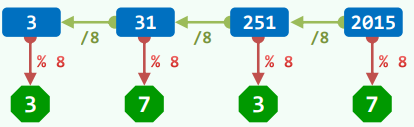
实现

原数的位数并不确定，因此不适合使用向量存储原数，并且浪费严重：

若使用向量，则扩容策略必须得当；
若使用列表，则多数接口均被闲置。

另外，运算的顺序与输出顺序相反——数位从低到高运算获得，但是输出却由高到低。这种相反的顺序非常符合栈的思想：

void convert( Stack<char> & S, __int64 n, int base ) {
	char digit[] = "0123456789ABCDEF"; //数位符号，如有必要可相应扩充
	while ( n > 0 ) //由低到高，逐一计算出新进制下的各数位
		{ S.push( digit[ n % base ] ); n /= base; } //余数入栈，n更新为除商
} //新进制下由高到低的各数位，自顶而下保存于栈S中
 
int main() {
	Stack<char> S; convert( S, n, base ); //用栈记录转换得到的各数位
	while ( ! S.empty() ) printf( "%c", S.pop() ); //逆序输出
}

括号匹配

思路尝试

核心思想：在括号串内部，消去一对紧邻的括号，不会影响全局的匹配判断。

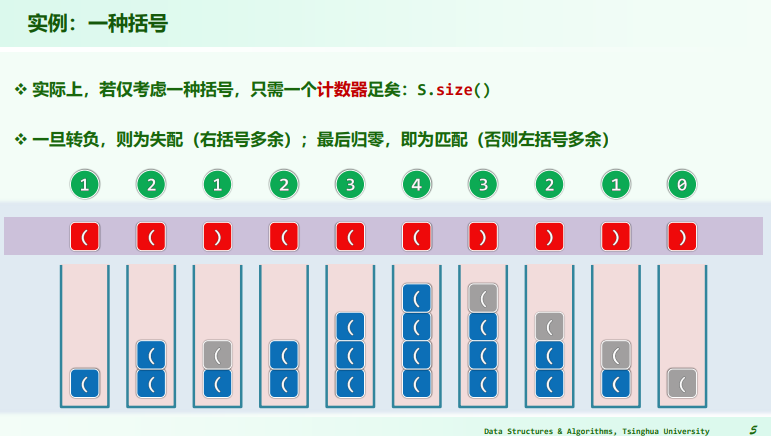
实现：一种括号

bool paren( const char exp[], Rank lo, Rank hi ) { //exp[lo, hi)
	Stack<char> S; //使用栈记录已发现但尚未匹配的左括号
	for ( Rank i = lo; i < hi; i++ ) //逐一检查当前字符
		if ( '(' == exp[i] ) S.push( exp[i] ); //遇左括号：则进栈
		else if ( ! S.empty() ) S.pop(); //遇右括号：若栈非空，则弹出对应的左括号
		else return false; //否则（遇右括号时栈已空），必不匹配
	return S.empty(); //最终栈空，当且仅当匹配
}

扩展：多类括号

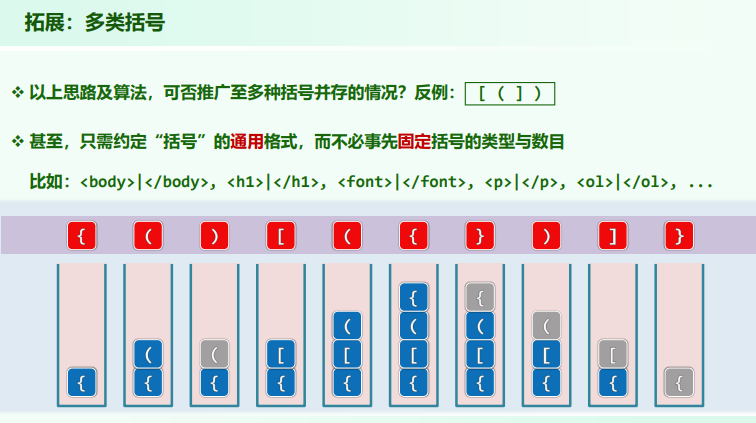
推广时要做括号类型的判断，直接根据左右是不能实现的；

栈混洗

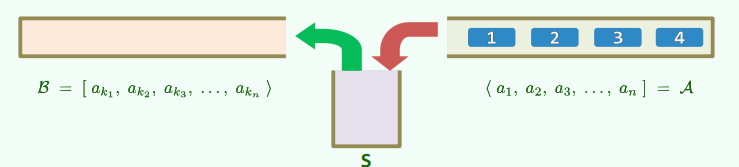
问题描述

对栈 A=<a1, a2, a3,.., an]，另有空栈 S 作中转、B 作转存处。A 只能弹出元素，B 只能压入元素，S 可以压入或弹出。经过一系列操作后，A 中所有元素转入 B 中，则 B 的当前从栈底到栈顶的序列称为对 A 的一次栈混洗：

栈混洗总数

同一输入序列有多种栈混洗，那么对长度为 n 的序列，栈混洗总数记作 SP(n)

显然，SP(1)=1 。考察当 S 变空时，即 A 的栈顶元素从 S 中弹出时，显然有 n 种情况：

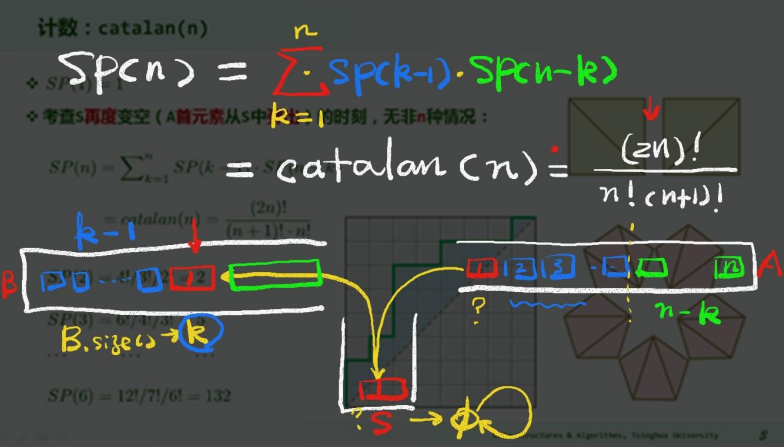
SP (n) = k = 1 \sum n SP (k - 1) \cdot SP (n - k) = c a t a l an (n) = \frac{( 2 n )!}{( n + 1 )! \cdot n !}

catalan 数应用⭐

栈混洗：catalan (n)
括号匹配 n 对：catalan (n)
二叉树形态 n 节点：catalan (n)
互异 BST 的数量 n 节点：catalan (n)
n 个叶节点的真二叉树数量：catalan (n-1)
- n 个叶节点的真二叉树，其中有内部节点 n-1个，故相当于 n-1个互异节点的 BST 的数量：Catalan(n-1)

禁形及其判断

若要判断输入序列的任一排列是否为栈混洗，则本质是判断相对次序是否符合栈的运算规律。

可以观察到并推广——任意三个元素能否按某相对次序出现于混洗中，与其它元素无关，即：对任何 1<=i<j<k<=n , [..., k,..., i,..., j,...> 一定不是栈混洗，这就是一个禁形。

$O (n^{3})$ 算法：逐个判断；
$O (n^{2})$ 算法：只需考虑 i<j 情况下，是否有 [...,j+1,...,i,...,j,...
$O (n)$ 算法：借助栈直接模拟栈混洗的过程，每次 pop 栈 S 时检查是否已空，或需弹出的元素在栈 S 中却不是栈顶，则必为禁形。

栈混洗与括号匹配

每一栈混洗，都对应于栈 S 的 n 次 push 和 pop 操作的一组序列，由括号匹配中的推广，push 和 pop 就是一对括号操作。因此 n 个元素的栈混洗，等价于 n 对括号的匹配：

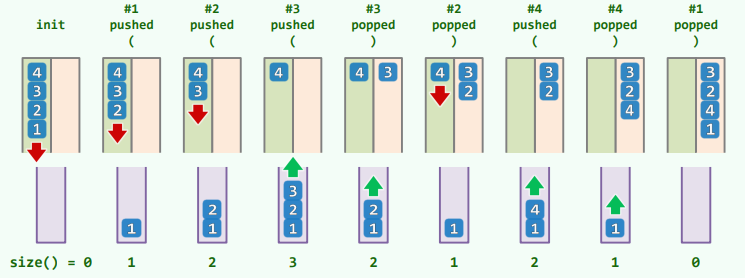
中缀表达式求值

问题描述

中缀表达式：就是运算符在两个操作数中间的计算式，如 1+1=2

自然地，中缀表达式求值的规则是基于优先级的局部计算，然后逐渐减治到全局——运算符逐渐减少，局部运算代以数值，最终得到结果。

设表达式 $S = S_{L} + S_{0} + S_{R}$ ，对 $S_{0}$ 可以优先计算（优先级局部最高）且 $v a l (S_{0}) = v_{0}$ ，则可以递推得化简式： $v a l (S) = v a l (S_{L} + s t r (v_{0}) + S_{R}$

思路

由于运算符优先级多样，并且还有括号可以改变局部运算的优先级——仅根据表达式的前缀，不足以确定各运算符的计算次序，只有获得足够的后续信息才能确定哪些运算符可以执行。

很自然地，这种读取顺序和运算顺序相反的情况，也适合用栈。栈在这里的作用，是缓冲了运算的及时需求：

自左向右扫描表达式，用栈记录已扫描的部分以及中间结果；
栈内最后所剩值（若非值，亦可判断表达式非法），就是表达式的正确结果。

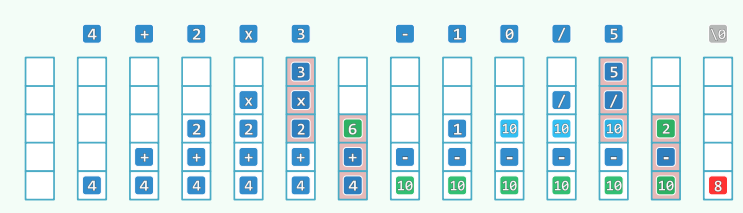
算法实现

//主算法
double evaluate( char* S, char* RPN ) { //S保证语法正确
	Stack<double> opnd; Stack<char> optr; //运算数栈、运算符栈
	optr.push('\0'); //哨兵首先入栈
	while ( ! optr.empty() ) { //逐个处理各字符，直至运算符栈空
		if ( isdigit( *S ) ) //若为操作数（可能多位、小数），则
			readNumber( S, opnd ); //读入
			append(RPN,opnd.top());//读入操作数并接至RPN末尾
		else //若为运算符，则视其与栈顶运算符之间优先级的高低
			// 根据不同的优先级切换到不同的运算情形
			switch( priority( optr.top(), *S ) ) {
				case '<': //栈顶运算符优先级更低
					optr.push( *S ); S++; break; //计算推迟，当前运算符进栈
		
				case ' =': //优先级相等（当前运算符为右括号，或尾部哨兵'\0'） 
					optr.pop(); S++; break; //脱括号并接收下一个字符
		
				case '>': {
					char op = optr.pop();
					append(RPN,op);
					if ( '!' == op ) opnd.push( calcu( op, opnd.pop() ) ); //一元运算符
					else { double opnd2 = opnd.pop(), opnd1 = opnd.pop(); //二元运算符
						opnd.push( calcu( opnd1, op, opnd2 ) ); //实施计算，结果入栈
					} //为何不直接：opnd.push( calcu( opnd.pop(), op, opnd.pop() ) )？
					break;
				} //case '>'
			} //switch
	}//while
	return opnd.pop(); //弹出并返回最后的计算结果
}

//优先级表
const char pri[N_OPTR][N_OPTR] = { //运算符优先等级 [栈顶][当前]
/* -- + */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* |  - */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* 栈 * */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 顶 / */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 运 ^ */ '>', '>', '>', '>', '>', '<', '<', '>', '>',
/* 算 ! */ '>', '>', '>', '>', '>', '>', ' ', '>', '>',
/* 符 ( */ '<', '<', '<', '<', '<', '<', '<', '=', ' ',
/* |  ) */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* -- \0 */ '<', '<', '<', '<', '<', '<', '<', ' ', '='
//           +    -    *    /    ^    !    (    )    \0
// |-------------- 当前运算符 --------------|
};

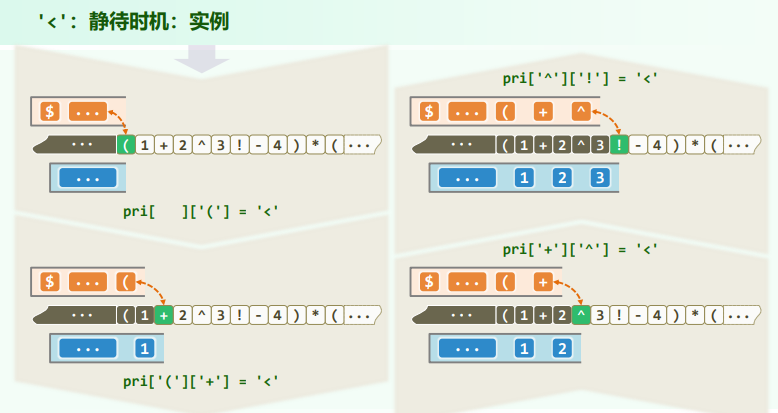
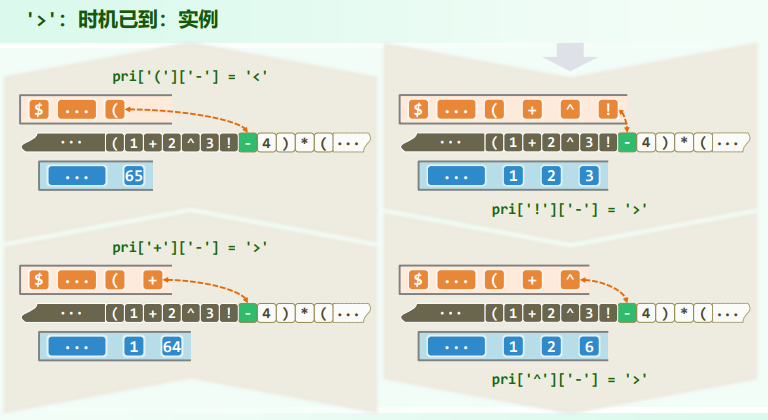
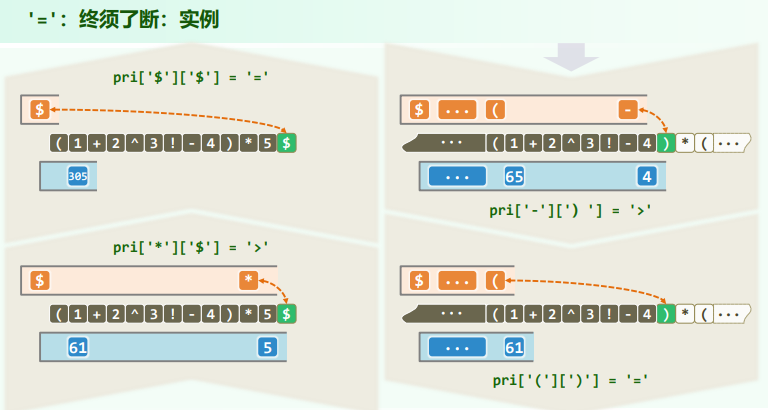
实例

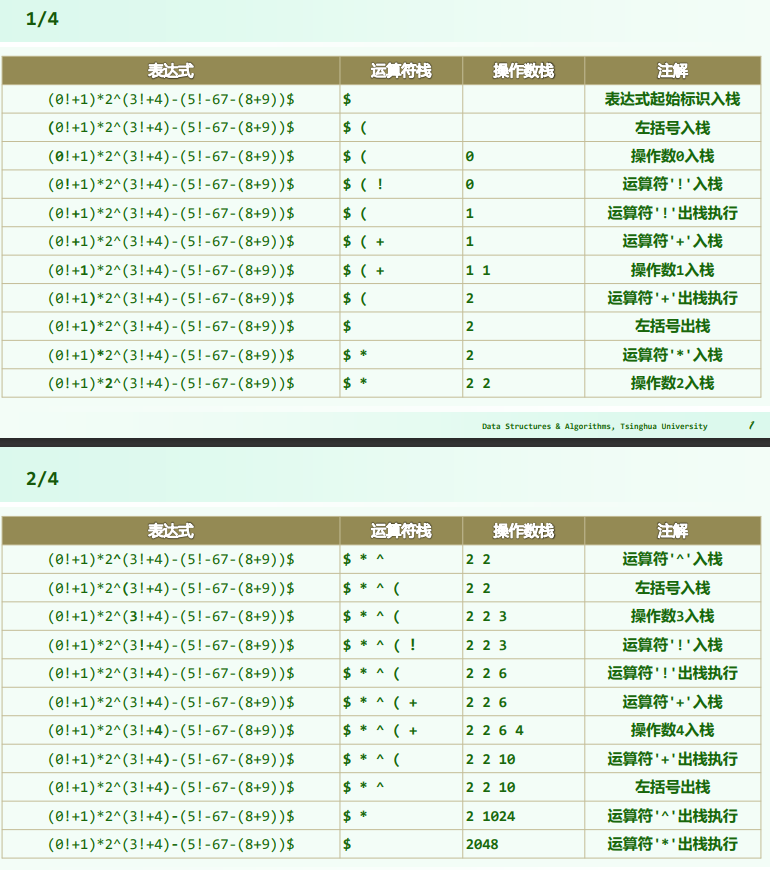
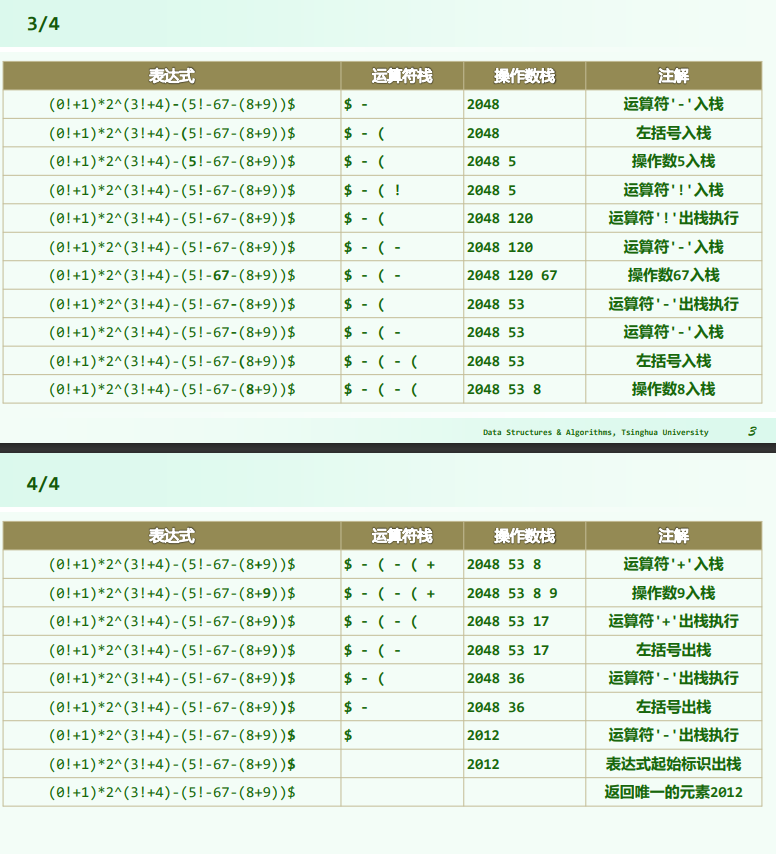
逆波兰表达式

定义

逆波兰表达式——后缀表达式：运算符在操作数之后，且不需要括号就可以表示优先级运算关系。

栈式求值

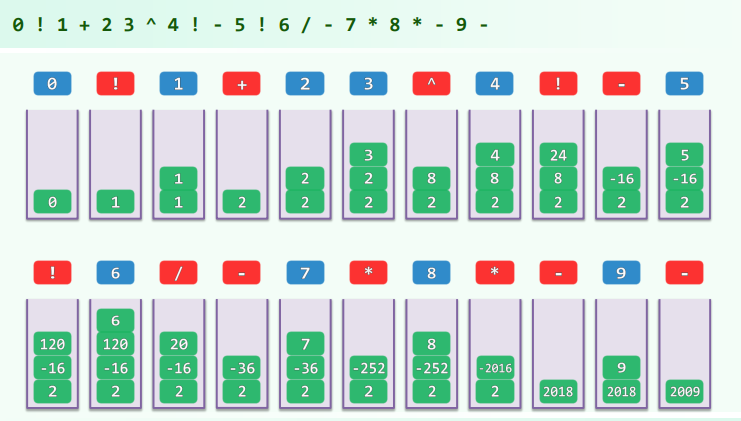
对后缀表达式：0! 123 + 4 5 6 ! * 7 ! 8 / + * 9 / + 计算方式如下：

引入栈 S 存放操作数：
逐个处理后缀表达式中下一元素 x，
- 若 x 是操作数，则压入栈 S，
- 否则弹出运算符 x 所需要的目的操作数，执行计算后再压入栈中
最后返回栈顶。

中缀表达式转后缀表达式

手动

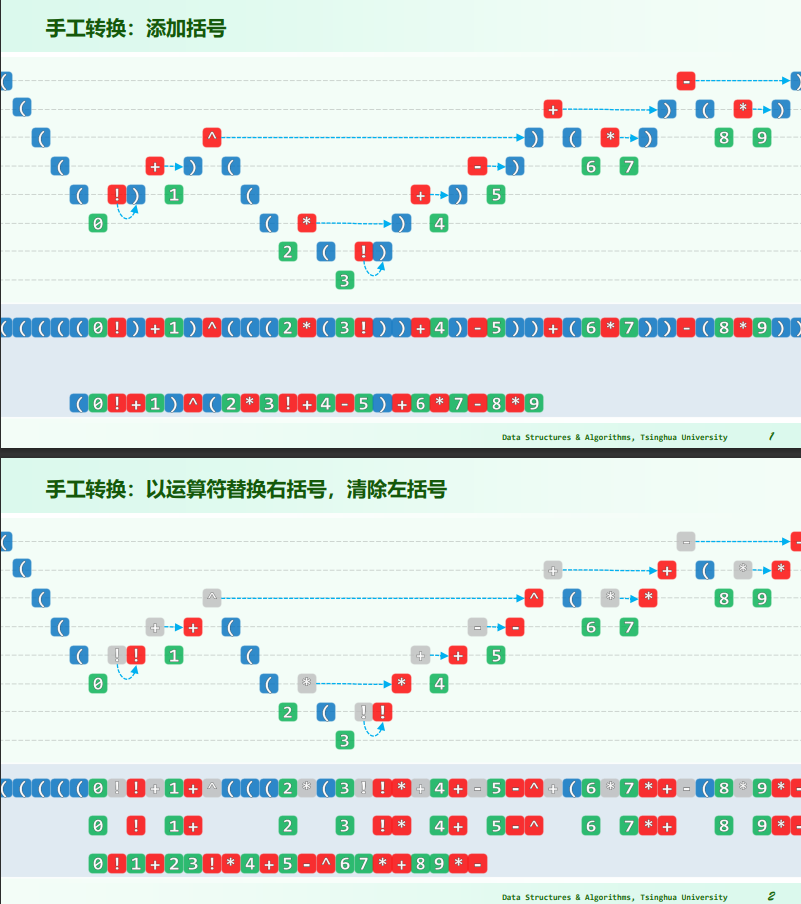
每遇到一个运算符，
- 若是一元运算符则与前面紧邻的操作数括起来，
- 若是二元运算符且后面的操作数满足与前面操作数的运行需求，则括起来；
最后将运算符移到最近的右括号之外；
脱去括号即可。

0! + 123 + 4 * (5 * 6! + 7! /8) /9 = ((0!) + 123) + 4 * ((5 * (6!)) + ((7!) /8)) /9 = ((0!) + 123) + ((4 * ((5 * (6!)) + ((7!) /8))) /9) = (((0!) + 123) + ((4 * ((5 * (6!)) + ((7!) /8))) /9)) = (((0)! 123) + ((4 ((5 (6)!) * ((7)! 8) /) +) * 9) /) + = 0! 123 + 456! * 7! 8/ + * 9/ +

自动

double evaluate ( char* S, char* RPN ) { 
	//对（已剔除白空格的）表达式S求值，并转换为逆波兰式RPN
	Stack<double> opnd; Stack<char> optr; //运算数栈、运算符栈
	optr.push ( '\0' ); //尾哨兵'\0'也作为头哨兵首先入栈
	while ( !optr.empty() ) { //在运算符栈非空之前，逐个处理表达式中各字符
		if ( isdigit ( *S ) ) { //若当前字符为操作数，则
			readNumber ( S, opnd );
			append ( RPN, opnd.top() ); //读入操作数，并将其接至RPN末尾
		} else //若当前字符为运算符，则
			switch ( priority ( optr.top(), *S ) ) { //视其与栈顶运算符之间优先级高低分别处理
				case '<': //栈顶运算符优先级更低时
					optr.push ( *S ); S++; //计算推迟，当前运算符进栈
					break;
				case '=': //优先级相等（当前运算符为右括号或者尾部哨兵'\0'）时
					optr.pop(); S++; //脱括号并接收下一个字符
					break;
				case '>': { //栈顶运算符优先级更高时，可实施相应的计算，并将结果重新入栈
					char op = optr.pop(); 
					append ( RPN, op ); //栈顶运算符出栈并续接至RPN末尾
					if ( '!' == op ) //若属于一元运算符
						opnd.push ( calcu ( op, opnd.pop() ) ); //则取一个操作数，计算结果入栈
					else { //对于其它（二元）运算符
						double opnd2 = opnd.pop(), opnd1 = opnd.pop(); //取出后、前操作数
						opnd.push ( calcu ( opnd1, op, opnd2 ) ); //实施二元计算，结果入栈
					}
					break;
				}
				default : exit ( -1 ); //逢语法错误，不做处理直接退出
			}//switch
	}//while
	return opnd.pop(); //弹出并返回最后的计算结果
}

Queue ADT

特点

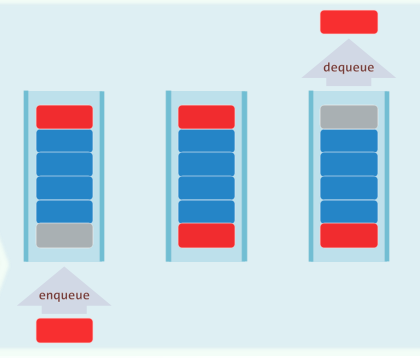
队列（queue）也是受限的序列：

只能在队尾插入（查询）：
- enqueue() / rear()
只能在队头删除（查询）：
- dequeue() / front()
先进先出（FIFO）、后进后出（LILO）

扩展接口：`getMax()`

class MaxQueue {
public:
    MaxQueue() {
        // 初始化数据队列和辅助队列
    }
 
    void enqueue(int value) {
        // 将元素插入数据队列
        dataQueue.push(value);
 
        // 将辅助队列中小于等于新元素的元素全部出队
        while (!maxQueue.empty() && maxQueue.back() < value) {
            maxQueue.pop_back();
        }
 
        // 将新元素插入辅助队列
        maxQueue.push_back(value);
    }
 
    int dequeue() {
        if (dataQueue.empty()) {
            return -1; // 队列为空
        }
 
        int front = dataQueue.front();
        dataQueue.pop();
 
        // 如果出队的元素是最大值，同时也出队辅助队列中的最大值
        if (front == maxQueue.front()) {
            maxQueue.pop_front();
        }
 
        return front;
    }
 
    int getMax() {
        if (maxQueue.empty()) {
            return -1; // 队列为空
        }
 
        return maxQueue.front();
    }
 
private:
    queue<int> dataQueue;      // 数据队列
    deque<int> maxQueue;       // 辅助队列，存储当前最大值
};
 
int main() {
    MaxQueue mq;
    mq.enqueue(1);
    mq.enqueue(3);
    mq.enqueue(2);
 
    cout << "Max: " << mq.getMax() << endl; // 输出最大值，应为3
 
    mq.dequeue();
    cout << "Max: " << mq.getMax() << endl; // 输出最大值，应为3
 
    mq.dequeue();
    cout << "Max: " << mq.getMax() << endl; // 输出最大值，应为2
 
    return 0;
}

使用 queap 结构实现

Queap

直方图最大矩形

44-Histogram-MaxRectangle-impl

问题描述

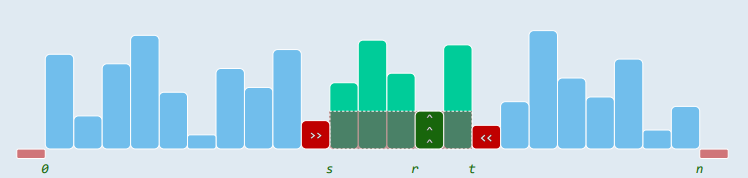在非负整数值的直方图区间 H[0, n) 中，如何找到最大的竖直矩形？显然求最大矩形面积的公式为： $ma x R ec t (r) = H [r] \cdot (t (r) - s (r))$ 这里

s (r)表示区间 [0,r] 上小于 H[r] 的最大值的坐标：
- $s (r) = ma x {k ∣0 \leq k \leq r an d H [k - 1] < H [r]}$
t (r)表示区间 [r,n] 上小于 H[r] 的最小值的坐标：
- $t (r) = min {k ∣ r < k \leq n an d H [r] > H [k]}$

暴力法

一一测试所有可能的 r 值，时间复杂度是 $O (n^{2})$ ，因为每一个 r 都要确定 $s (r)$ 和 $t (r)$

using Rank = unsigned int;
 
// 按定义蛮力地计算直方图H[]中的最大矩形（多个并列时取最靠左侧者）
int mr_BRUTE( int H[], Rank n, Rank& mr_r, Rank& mr_s, Rank& mr_t ) {
   int maxRect = 0;
   for ( Rank r = 0, s = 0, t = 0; r < n; r++, s = t = r ) {
      do s--; while ( (-1 != s) && (H[s] >= H[r]) ); s++;
      do t++; while ( (t < n) && (H[r] <= H[t]) );
      int rect = (int) H[r] * ( t - s );
      if ( maxRect < rect )
         { maxRect = rect; mr_r = r; mr_s = s; mr_t = t; }
   }
   return maxRect;
} //每个极大矩形耗时O(n)，累计O(n^2)

使用栈

int mr_STACK( int H[], Rank n, Rank& mr_r, Rank& mr_s, Rank& mr_t ) { //除末项-1哨兵，H[]皆非负
	Rank* s = new Rank[n]; Stack<Rank> S; //自右可见项的秩
	for( Rank r = 0; r < n; r++ ) { //依次计算出
		while ( !S.empty() && ( H[S.top()] >= H[r] ) ) S.pop(); //每一个s(r)
		s[r] = S.empty() ? 0 : 1 + S.top();
		S.push(r); // S总是处于递增状态
	}
	while( !S.empty() ) S.pop();
 
	Rank* t = new Rank[n]; Stack<Rank> T; //自左可见项的秩
	for( Rank r = n-1; -1 != r; r-- ) { //依次计算出
		while ( !T.empty() && H[r] <= H[T.top()] ) T.pop(); //每一个t(r)
		t[r] = T.empty() ? n : T.top();
		T.push(r);
	}
	while( !T.empty() ) T.pop();
 
	int maxRect = 0;
	for( Rank r = 0; r < n; r++ ) {
		int mR = H[r] * (t[r] - s[r]);
		if ( maxRect < mR )
		{ maxRect = mR; mr_r = r; mr_s = s[r]; mr_t = t[r]; }
		}
	delete [] s; delete [] t;
	return maxRect;
} //每项进栈、出栈不过常数次，累计成本O(n)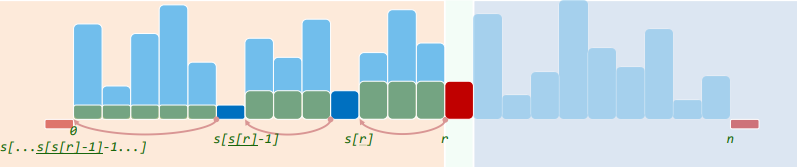

每一轮循环的结束，S 都会存储一串 s[]，有如下关系： $S [S . s i ze () - 1] = S . t o p () = r$ 并且 $\forall0 \leq k < S . s i ze (), S [k - 1] + 1 = s [S [k]]$

One-pass

对于 $t (r)$ 而言，只有当输入完全结束后才能开始，不是一个在线算法。若要改进到 $s (r)$ 和 $t (r)$ 都只是一轮扫描确定：

int mr_STACK( int H[], Rank n, Rank& mr_r, Rank& mr_s, Rank& mr_t ) { //H[]皆非负
	Stack<Rank> SR; //次栈顶、栈顶总是s[r]-1与r，当前的t = t[r]
	int maxRect = 0;
	for (Rank t = 0; t <= n; t++ ) { //逐个尝试以t为右边界的
		while ( !SR.empty() && ( t == n || H[SR.top()] > H[t] ) ) { //每一个极大矩形
			Rank r = SR.pop(), s = SR.empty() ? 0 : SR.top() + 1;
			int mR = H[r] * ( t - s );
			if ( maxRect < mR )
			{ maxRect = mR; mr_r = r; mr_s = s; mr_t = t; }
		}
		if ( t < n ) SR.push( t ); //栈中只记录所有的H[s] = min{ H[k] | s <= k <= t }
	} //assert: SR is empty at exit
	return maxRect;
} //每项进栈、出栈不过常数次，累计成本O(n)

每一次外部循环中，总有： $\forall0 \leq k > SR . s i ze (), SR [k - 1] + 1 = s [SR [k]]$ 对每个内层循环中弹出的 r，有： $t (r) = t$ 并且 $s [r] = SR . t o p () + 1$

栈堆与队列堆

Steap

Steap = Stack + Heap = push + pop + getMax

使用两个栈 S 和 P，S 存储数据，P 则存储 S 中对应后缀的最大者（即 S.getMax()）

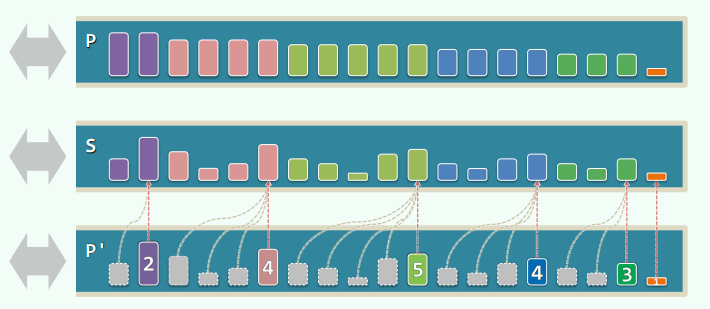
ADT:

Steap::getMax(){return P.top();}
Steap::pop(){P.pop(); return S.pop();}//O(1)
Steap::push(){P.push(max(e,P.top()));S.push(e);}//O(1)

Queap

Queap = Queue + Heap = enqueue + dequeue + getMax

使用两个队列 Q 和 P，Q 存储数据并且是单进单出；P 存放 Q 的后缀的最大值，并且允许队尾插入和删除两种操作，即单进双出：

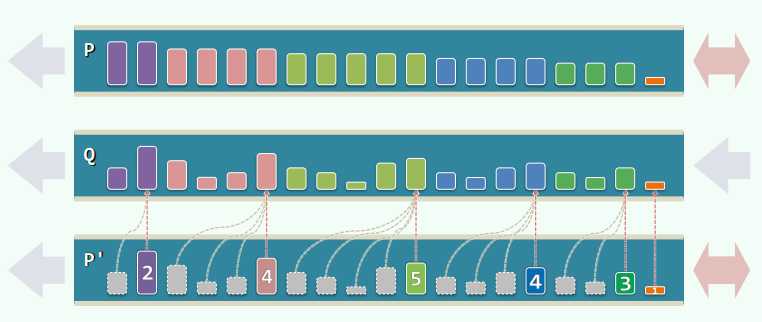
ADT：

Queap::getMax(){return P.front();}
Queap::dequeue(){P.dequeue();return Q.dequeue();}//O(1)
Queap::enqueue(e){Q.enqueue(e);P.enqueue(e);for(x=P.rear();x && (x->key <=e);x=x->pred) x->key=e;} // 最坏O(n)

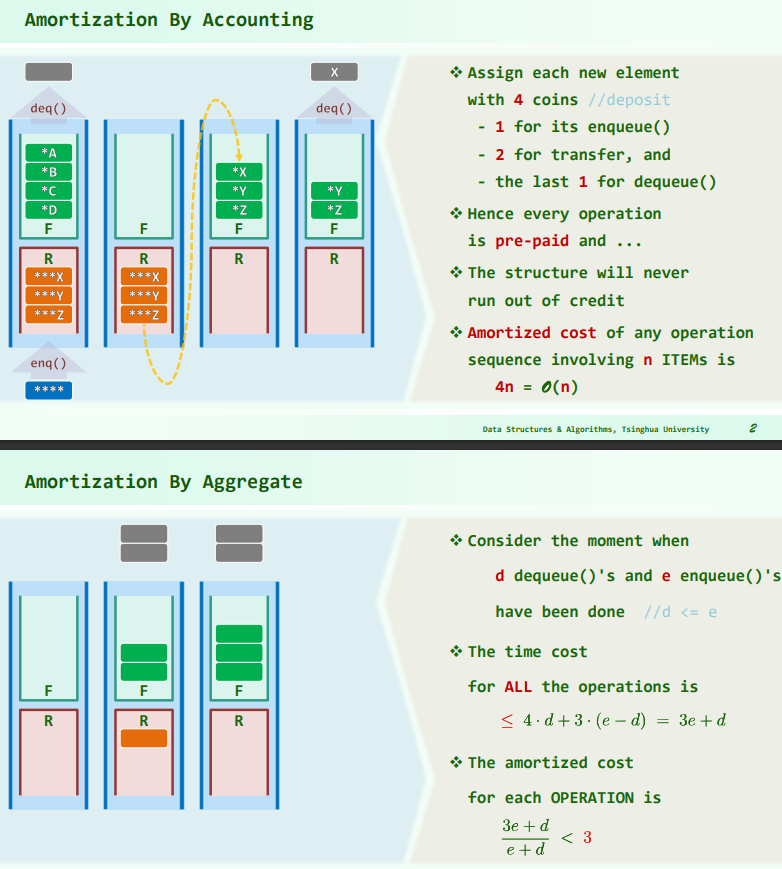
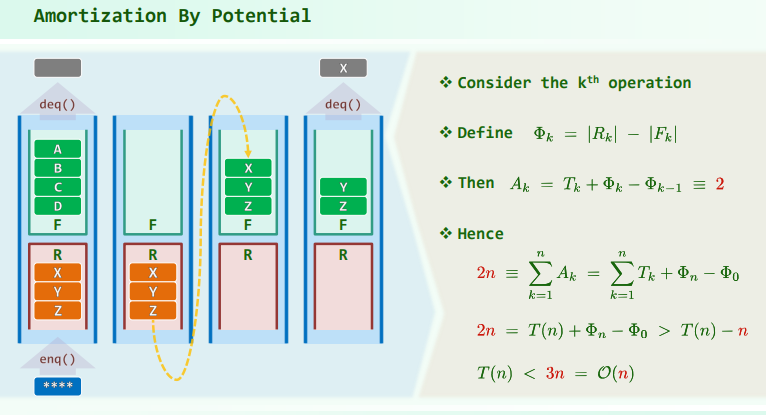
双栈当队

ADT

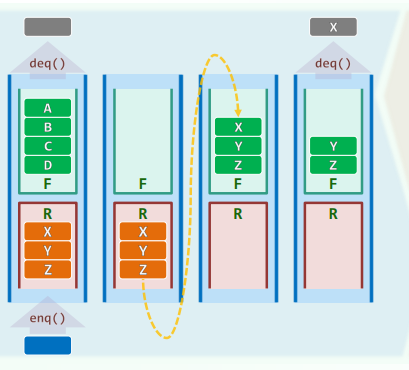
def Q.enqueue(e)
	R.push(e)
 
def Q.dequeue()
	if(F.empty())
		while(!R.empty())
			F.push(R.pop());
	return F.pop();

复杂度（均摊）

最好情况： $O (1)$ 最坏情况： $O (n)$

习题：41-Stack-queue-Exercise

🌰Senjl's Digital Garden🇨🇳

Explorer

40-Stack_Queue

Stack ADT

扩展接口 ：getMax()

使用 steap 结构实现

函数调用栈

原理

深度与空间

递归法求阶乘

递归求 fib 序列

空间复杂度

消除递归

尾递归

定义

特点

消除尾递归

进制转换

数制转换原理

实现

括号匹配

思路尝试

实现：一种括号

扩展：多类括号

栈混洗

问题描述

栈混洗总数

catalan 数应用⭐

禁形及其判断

栈混洗与括号匹配

中缀表达式求值

问题描述

思路

算法实现

实例

逆波兰表达式

定义

栈式求值

中缀表达式转后缀表达式

手动

自动

Queue ADT

特点

扩展接口 ：getMax()

使用 queap 结构实现

直方图最大矩形

问题描述

暴力法

使用栈

One-pass

栈堆与队列堆

Steap

Queap

双栈当队

ADT

复杂度（均摊）

Graph View

Table of Contents

Backlinks

扩展接口：`getMax()`

扩展接口：`getMax()`