2018-final

B-tree

考查包含2018个关键码的16阶 B-树，约定根节点常驻内存，且在各节点内部采用顺序查找。

1. 在单次成功查找的过程中，至多可能需要读多少次磁盘？请列出估算的依据。

至多读磁盘次数=B 树的最大高度，即 $h\le 1+\lfloor {\log }_{\lceil \frac{M}{2}\rceil }\frac{N+1}{2}\rfloor =1+\lfloor {\log }_{\lceil \frac{16}{2}\rceil }\frac{2018+1}{2}\rfloor =4$

2. 在单次成功查找的过程中，至多可能有多少个关键码需要不目标关键码做比较？请列出估算的依据。

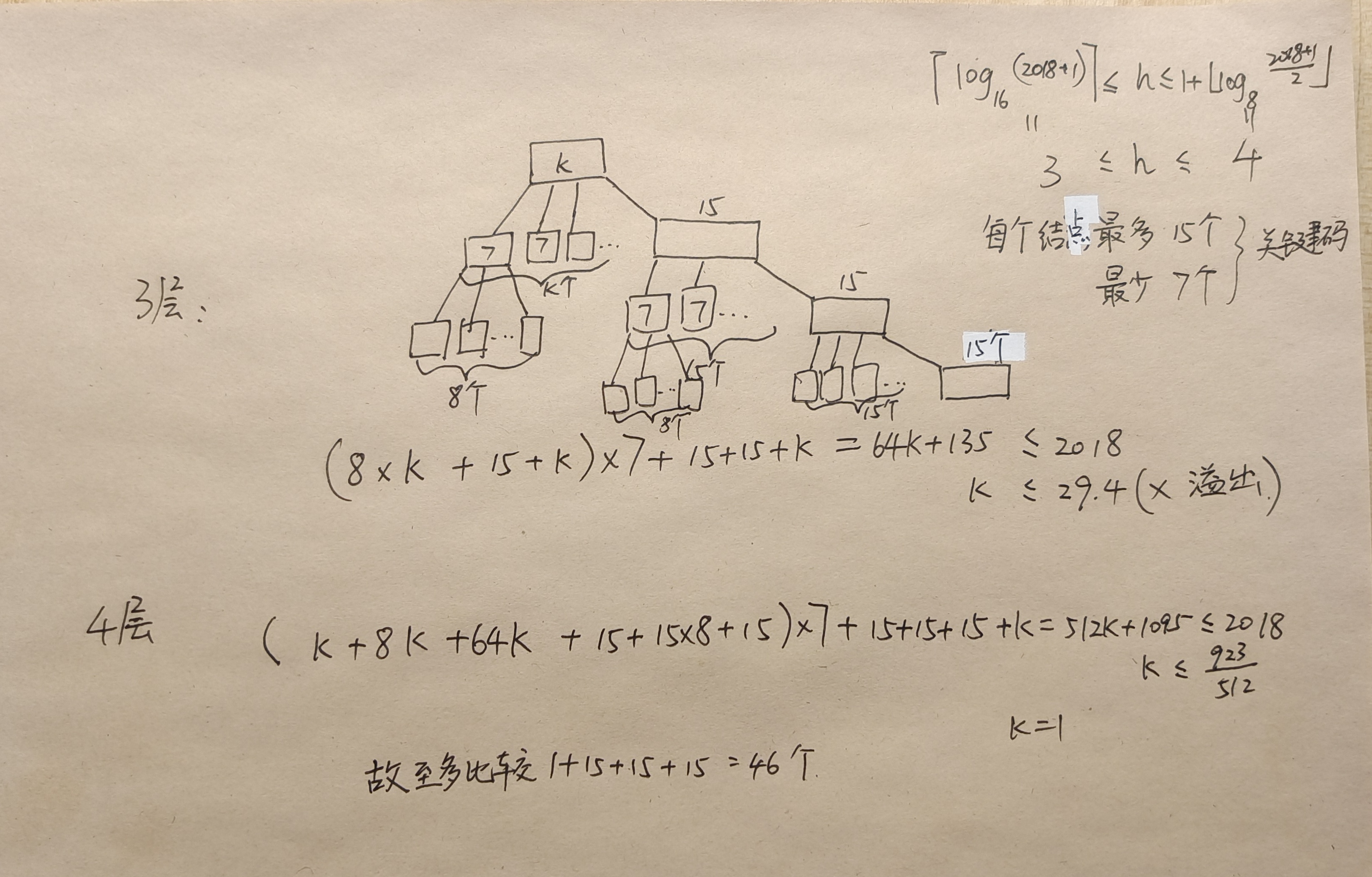
扩展：若上题给关键码数为 1024，至多比较关键码数又是多少？

显然根据四层公式 $512k+1095>1024$，因此这些关键码不足以支撑起 4 层并且右侧节点是 15 个关键码的 BTree。 考虑三层，则有 $64k+135<=1024$ 解得 $k<=13.88$，即 k=13，则至多关键码比较数为 13+15+15=43

理想随机

本课程所介绍的一些算法与数据结构，乃是针对实际应用中普遍存在的非随机数据集而设计的；反过来，只要数据集是理想随机的，则大可不必采用。试举三个这样的案例，列出讲义页码，并作简要说明（各不超过两行）

1. BST 如果理想随机，就没有必要平衡化
2. 除余法中如果 key 足够理想随机，那么 hash 表长就没有必要必须是质数；
3. 如果文本串和模式串出现的概率足够随机，那么 KMP 算法的效率和暴力算法一致。

判断

1. 某节点被删除后 AVL 树的高度即便下降了，这次操作期间也未必经过旋转调整。

✅ AVL-tree树高降低的可能性：一定要失衡吗？

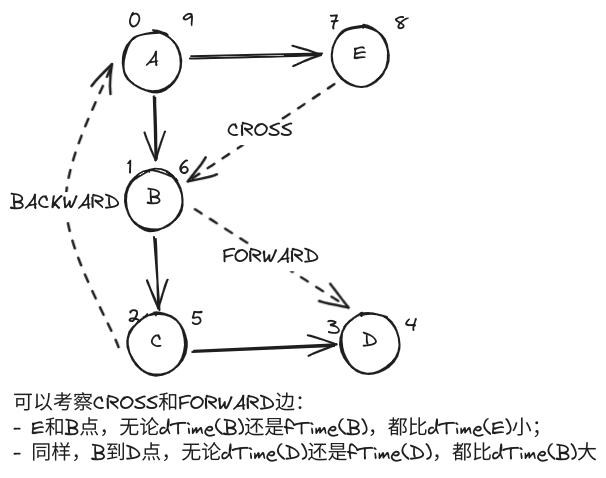
2. 图的 DFS 算法中的 default 分支，将 dTime(v)<dTime(u) 改为 dTime(v)<fTime(u) 同样可行。

❌ 正确答案是 ✅ 解答如下图

3. 有向图经 DFS 后若共有 k 条边被标记为 BACKWARD，则应该恰有 k 个环路。

✅

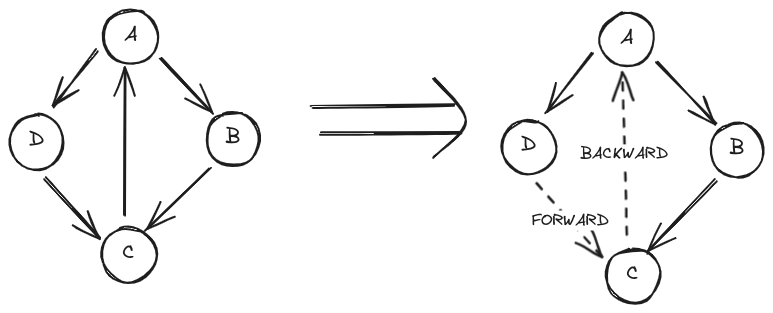
正确答案：❌ 这里注意是有向图，有向图由于存在 FORWARD 和 CROSS 边，因此并不能保证非 TREE 边一定是 BACKWARD，因此也就不能保证环路数等于 BACKWARD 边数。举例如下图：

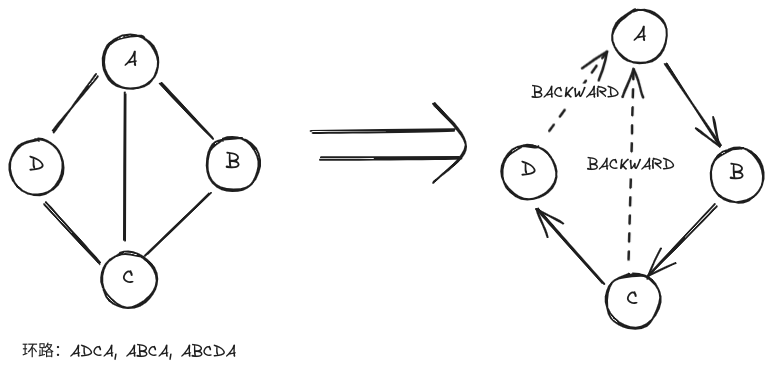
但是无向图只有 BACKWARD，能够保证其中的环路数和 BACKWARD 边数一致吗？答案也是否定的：

4. 左式堆中每一对兄弟节点的高度尽管未必左大右小，但左兄弟至少不低于右兄弟的一半。

❌ 此图中，1、2互为左右兄弟，但左兄弟远小于右兄弟高度的一半。

5. 对于同一无向图，起始于顶点 s 的 DFS 尽管可能得到结构不同的 DFS 树，但 s 在树中的度数必然固定。

✅ 相当于 DAG 的零入度拓扑排序， 或者双连通图，若 s 是关节点，则度数为 k（极大双连通分量的数量），若 s 不是关节点，则度数为 1

6. 采用 Crane 算法将左式堆 A 与 B 合并为左式堆 H，则 H 右侧链上的节点未必都来自 A 或 B 的右侧链。

✅ 左右侧链可能颠倒

7. 采用单向平方试探策略的散列表，只要长度 M 不是素数，则每一组同义词在表中都不会超过 $\lfloor M/2\rfloor$。

✅ 平方试探

8. 经快速划分 LGU 版之后，后缀 G 中的雷同元素可能调换相对次序，但其余部分的雷同元素绝不会。

✅ 习题 12-1：12-1 构造轴点的 LGU 策略

9. PFS 过程中，尽管每一步迭代都可能多次调用 prioUpdater ()，但累计不超过 O (e)次。

❌ ✅ 这个题是对的

算法框架

template <typename Tv, typename Te> 
template <typename PU> //优先级搜索（全图）
void Graph<Tv, Te>::pfs( Rank s, PU prioUpdater ) { // s < n
	reset(); //全图复位
	for ( Rank v = s; v < s + n; v++ ) //从s起顺次检查所有顶点
	    if ( UNDISCOVERED == status( v % n ) ) //一旦遇到尚未发现者
	        PFS( v % n, prioUpdater ); //即从它出发启动一次PFS
} //如此可完整覆盖全图，且总体复杂度依然保持为O(n+e)

template <typename Tv, typename Te>
template <typename PU> //顶点类型、边类型、优先级更新器
void Graph<Tv, Te>::PFS( Rank v, PU prioUpdater ) { //优先级搜索（单个连通域）
	priority( v ) = 0;
	status( v ) = VISITED; //初始化，起点v加至PFS树中
	
	while ( 1 ) { //将下一顶点和边加至PFS树中
	    for ( Rank u = firstNbr( v ); - 1 != u; u = nextNbr( v, u ) ) //对v的每一个邻居u
	        prioUpdater( this, v, u ); //更新其优先级及其父亲
	    int shortest = INT_MAX;
	    for ( Rank u = 0; u < n; u++ ) //从尚未加入遍历树的顶点中，选出下一个优先级
	        if ( ( UNDISCOVERED == status( u ) ) && ( shortest > priority( u ) ) ) //最高的
	            { shortest = priority( u ), v = u; } //顶点v
	    if ( shortest == INT_MAX ) break; //直至所有顶点均已加入
	    status( v ) = VISITED; type( parent( v ), v ) = TREE; //将v加入遍历树
	}//while
} //通过定义具体的优先级更新策略prioUpdater，即可实现不同的算法功能

指向原始笔记的链接

仔细看 PFS 的 while 循环，其中有前后两个循环，而前一循环中才有 prioUpdater，而执行 prioUpdater 的条件，则是选择到 v 的正确的邻居，而不重复地（或者说，逆向地）遍历每个顶点的邻居，最后得到的恰好就是全图的边数。

至于 PPT 上说前一循环在邻接表实现的时间复杂度是 O(n+e)，而邻接矩阵的实现是 O(n^2)，这是由于 nextNbr 的调用决定的，邻接表中调用 nextNbr 的复杂度为 O(1)，而邻接矩阵中为 O(n)。

10. 只要底层的排序算法是正确且稳定的，则 radixSort ()也必然是正确且稳定的。

✅ 基数排序如何确保正确性？底层排序一定要稳定吗？

11. 相对于 KMP 算法而言，BM 算法更适合于大字符集的应用场合。

✅

12. 若调用 BST::remove(e) 将节点 x 从常规 BST 中删除，则所需时间为被删除之前 x 的深度。

❌ 如果是内部节点，则还需要找到 x 的直接后继。

13. 在存有 n 个词条的跳转表中，各塔高度的期望值为 $\Theta (\log n)$。

❌ expected-height = 2 = O(1)

14. 将 n 个词条逐个插入一个容量为 M、采用线性试探策略、初始为空的散列表，n<M，则无论它们的插入次序如何，最终的平均查找长度必然一致。

✅

15. 红黑树的插入或删除操作，都有可能导致 $\Omega (\log n)$ 个节点的颜色反转。

✅ 相当于 B 树的上溢或下溢。（RR-2 和 BB-2B）

16. 只有在访问序列具有较强的局部性时，伸展树才能保证分摊 $O(\log n)$ 的性能。

❌

17. 将 {0,1,2,…, 2018} 插入一棵空的伸展树后若树高为 2018，则上述词条必是按单调次序插入的。

✅

18. 相对于同样规模的完全二叉堆，多叉堆 delMax ()操作的时间成本更低。

❌ 有一定争议，但是选❌是不会错的。虽然 PPT 上说在 d>4 时下滤成本增加至 $d\cdot {\log }_{d}n$，但是三叉堆的下滤操作实际上是更低的，并且四叉堆的下滤操作虽说和二叉堆复杂度一致，但由于缓存的原因，实际效率也要更高。

参考资料：

• ics.uci.edu/~eppstein/261/lecture5a.pdf
• d-ary heap - Wikipedia

19. 在插入操作后若红黑树的黑高度增加，则在双红修复过程中仅做过重染色，无需任何结构调整。

✅ RR-2

20. 最底层的叶节点一旦被访问（并做过 splay 调整）之后，伸展树的高度必然随即下降。

❌ 这里反而上升。

21. 若输入序列包含 $\Omega (n^2)$ 个逆序对，则快速排序算法 LUG 版至少需要经过 $\Omega (n\log n)$ 次元素交换操作。

✅

22. 胜者树的根节点即是总冠军，而败者树的根节点即是亚军。

❌ 其实这里我觉得有歧义，亚军并不一定是全局次强者，如果全局次强者第一轮遇到冠军，即会被淘汰。

23. 采用 12-C 节中介绍的任何一种增量序列，shellSort ()最后的 1-sorting 都只需要 $O(n)$ 的时间。

❌ shell 序列最坏情况下仍需要 $\Omega (n^2)$ 的时间。

24. B-Tree 的任一非叶节点内，每个关键码都存在直接后继，且必然来自某个叶节点。

✅

25. 无论是单独借助 BC 表或 GS 表，BM 算法在最好情况下都只需要 $O(|T|/|P|)=O(n/m)$ 的时间。

✅

26. shellSort ()每按照某个增量做过逐列排序，序列中逆序对的总数都会减少或持平，但绝不致增加。

✅ 即使 shell 序列也会满足。

27. 对规模为 n 的 AVL 树做一次插入操作，最坏情况下可能引发 $\Omega (\log n)$ 次局部重构。

❌ 考虑最坏情况 Fib-AVL 树，最坏情况也只不过是 $O(1)$ 次重构。

28. 若采用完全二叉堆来实现 PFS，则各顶点在出堆之前，深度只可能逐步减少或保持，而不致增加。

✅ 完全二叉堆的特点，高层节点在删除时不会下降。

封闭散列

某散列表 $H[0,M=2^s]$ 采用封闭散列策略（初始令 c=d=0 )：对于任何 key ，首先试探 $H[key\%M]$ ；以下，只要冲突，就令 c<-c+1 再 d<-d+c ，并继而试探 $H[(key+d]\%M$。以 $M=2^4=16$ 为例，关键码 key=27 的前五个试探位置依次是：11、12、14、1、5。但如同对于平方试探策略，我们首先需要确认，这种试探序列是否总能覆盖所有桶单元。若是，请给出证明；否则，试举一（ s 和 key 组合的）反例。

s=3, H (key)=4的地方永远无法填上。证明方法就是得到 d 的递推公式，再画函数曲线

多产的计算机科学家

计算机科学家往往在多个方面同时有所建树。试以讲义上介绍的算法或数据结构为例，列举出其中的三位，以及他们各自的两项贡献。请注明在讲义上对应的页码，并作简要说明（每人每项不超过一行）

1. Dijkstra：SPT algo、哲学家就餐问题、信号量
2. Tarjan：LCA 算法、Splay 双层伸展、强连通分量算法、fibonacci heap、中位数选取算法、并查集
3. Floyd：快速建堆法、Floyd-Warshall algo、环路检测
4. Knuth: KMP algo、计算复杂度理论、TeX 排版系统、The Art of Computer Programming

KMP

所谓 Fibonacci Strings，系由字符集 $\Sigma ={\{}^{\prime }{O}^{\prime }{,}^{\prime }{X}^{\prime }\}$ 组成：

• ${\varphi }_0$ = "O"
• ${\varphi }_1$ = "X"
• 对于 k>=2，有 ${\varphi }_k={\varphi }_{k-1}{\varphi }_{k-2}$，如 ${\varphi }_2$ = "XO", ${\varphi }_3$ = "XOX", ${\varphi }_4$ = "XOXXO",…

1. 以下考查 KMP 算法的改进版，试列出 ${\varphi }_8$ 并给出对应查询表。

${\varphi }_8$ 太长了，这里写个 ${\varphi }_7$ 意思意思。

j	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
${\varphi }_7[j]$	X	O	X	X	O	X	O	X	X	O	X	X	O	X	O	X	X	O	X	O	X
imp-next[j]	-1	0	-1	1	0	0	3	-1	1	0	0	1	1	2	3	0	1	1	2	3	-1

2. 若 $|\varphi |>2$，则将 $\varphi$ 末尾的两个字符翻转，得到的串记作 ${\varphi }^{{}^{\prime }}$，如 ${\varphi }_5^{{}^{\prime }}$ = XOXXOXXO。试证明：$\forall k\ge 2,{\varphi }_{k-2}{\varphi }_{k-1}={\varphi }_k^{{}^{\prime }}$

归纳法证明。 k=3 时，${\varphi }_3^{{}^{\prime }}$ = "XXO"，而 ${\varphi }_1{\varphi }_2$ = "XXO" 满足要求。 假设 $\forall k\ge 2,{\varphi }_{k-2}{\varphi }_{k-1}={\varphi }_k^{{}^{\prime }}$ 成立，那么… 不会了

3. 试证明：若以 ${\varphi }_k$ 做为模式串，文本串的某个 $T[i]$ 可能参与 $\Omega (k)$ 次比较。

4. 试证明，对于任何模式串 P，文本串的每一字符至多会与 P 中的 $O\log m$ 个字符做比对，$m=|P|$。