Applications of Catalan Numbers

Math formula

Catalan numbers are defined using below formula:

C a t a l an (n) = \frac{( 2 n )!}{( n + 1 )! \cdot n !} = k = 2 \prod n \frac{n + k}{k}, f or n > 0

Catalan numbers can also be defined using following recursive formula.

C a t a l an (0) C a t a l an (n + 1) = 1, = i = 0 \sum n (C a t a l an (i) \cdot C a t a l an (n - i))

The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …

Implementation

recursive version

#include <iostream>
using namespace std;
 
// A recursive function to find nth catalan number
unsigned long int catalan(unsigned int n)
{
	// Base case
	if (n <= 1)
		return 1;
 
	// catalan(n) is sum of
	// catalan(i)*catalan(n-i-1)
	unsigned long int res = 0;
	for (int i = 0; i < n; i++)
		res += catalan(i) * catalan(n - i - 1);
 
	return res;
}
 
// Driver code
int main()
{
	for (int i = 0; i < 10; i++)
		cout << catalan(i) << " ";
	return 0;
}

Time Complexity: O (2^n) The above implementation is equivalent to nth Catalan number.

$T (n) = i = 0 \sum n - 1 T (i) * T (n - i - 1) f or n \geq 1;$

The value of nth Catalan number is exponential which makes the time complexity exponential.

Auxiliary Space: O(n)

dynamic programming version

We can observe that the above recursive implementation does a lot of repeated work. Since there are overlapping subproblems, we can use dynamic programming for this.

Below is the implementation of the above idea:

Create an array catalan[] for storing ith Catalan number.
Initialize, catalan[0] and catalan[1] = 1
Loop through i = 2 to the given Catalan number n.
- Loop through j = 0 to j < i and Keep adding value of catalan[j] * catalan[i – j – 1] into catalan[i].
Finally, return catalan[n]

Follow the steps below to implement the above approach:

#include <iostream>
using namespace std;
 
// A dynamic programming based function to find nth
// Catalan number
unsigned long int catalanDP(unsigned int n)
{
	// Table to store results of subproblems
	unsigned long int catalan[n + 1];
 
	// Initialize first two values in table
	catalan[0] = catalan[1] = 1;
 
	// Fill entries in catalan[] using recursive formula
	for (int i = 2; i <= n; i++) {
		catalan[i] = 0;
		for (int j = 0; j < i; j++)
			catalan[i] += catalan[j] * catalan[i - j - 1];
	}
 
	// Return last entry
	return catalan[n];
}
 
// Driver code
int main()
{
	for (int i = 0; i < 10; i++)
		cout << catalanDP(i) << " ";
	return 0;
}

Time Complexity: O(n^2)
Auxiliary Space: O(n)

Binomial Coefficient Solution

We can also use the below formula to find nth Catalan number in O(n) time.

C a t a l an (n) = \frac{1}{n + 1} (n 2 n) = \frac{( 2 n )!}{( n + 1 )! \cdot n !}

In the pascal triangle,

							1 
                      1         1
                 1        2        1 
             1       3         3       1 
        1      4         6       4         1
   1     5         10     10       5         1

the formula for a cell of Pascal’s triangle:

C_{n}^{k} = (k n) = \frac{n !}{k ! \cdot ( n - k )!}

Below are the steps for calculating $n C_{r}$ .

Create a variable to store the answer and change r to n – r if r is greater than n – r because we know that C(n, r) = C(n, n-r) if r > n – r
Run a loop from 0 to r-1
- In every iteration update ans as *(ans(n-i))/(i+1)**, where i is the loop counter.
So the answer will be equal to ((n/1) * ((n-1)/2) * … * ((n-r+1)/r), which is equal to $n C_{r}$ .

Below are steps to calculate Catalan numbers using the formula: 2nCn/(n+1)

Calculate $2 n C_{n}$ using the similar steps that we use to calculate $n C_{r}$
Return the value $2 n C_{n} / (n + 1)$

Below is the implementation of the above approach:

// C++ program for nth Catalan Number
#include <iostream>
using namespace std;
 
// Returns value of Binomial Coefficient C(n, k)
unsigned long int binomialCoeff(unsigned int n,
								unsigned int k)
{
	unsigned long int res = 1;
 
	// Since C(n, k) = C(n, n-k)
	if (k > n - k)
		k = n - k;
 
	// Calculate value of [n*(n-1)*---*(n-k+1)] /
	// [k*(k-1)*---*1]
	for (int i = 0; i < k; ++i) {
		res *= (n - i);
		res /= (i + 1);
	}
 
	return res;
}
 
// A Binomial coefficient based function to find nth catalan
// number in O(n) time
unsigned long int catalan(unsigned int n)
{
	// Calculate value of 2nCn
	unsigned long int c = binomialCoeff(2 * n, n);
 
	// return 2nCn/(n+1)
	return c / (n + 1);
}
 
// Driver code
int main()
{
	for (int i = 0; i < 10; i++)
		cout << catalan(i) << " ";
	return 0;
}

Time Complexity: O(n).
Auxiliary Space: O(1)

Applications

Number of possible Binary Search Trees with n keys.
Number of expressions containing n pairs of parentheses which are correctly matched. For n = 3, possible expressions are ((())), ()(()), ()()(), (())(), (()()).
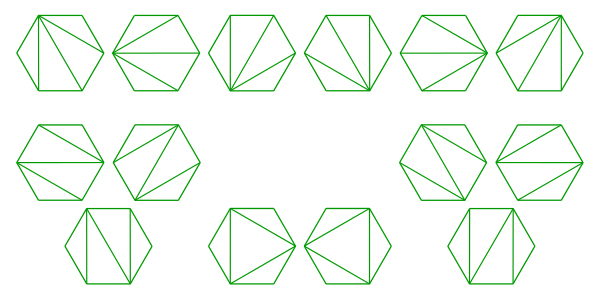
Number of ways a convex polygon of n+2 sides can split into triangles by connecting vertices.
Number of full binary trees (A rooted binary tree is full if every vertex has either two children or no children) with n+1 leaves.
Number of different Unlabeled Binary Trees can be there with n nodes.
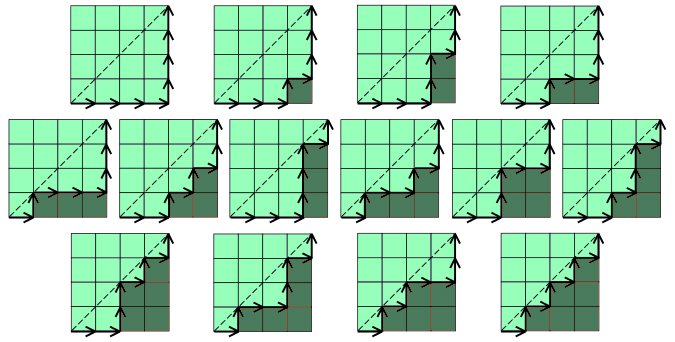
The number of paths with 2n steps on a rectangular grid from bottom left, i.e., (n-1, 0) to top right (0, n-1) that do not cross above the main diagonal.
Number of ways to insert n pairs of parentheses in a word of n+1 letters, e.g., for n=2 there are 2 ways: ((ab)c) or (a(bc)). For n=3 there are 5 ways, ((ab)(cd)), (((ab)c)d), ((a(bc))d), (a((bc)d)), (a(b(cd))).
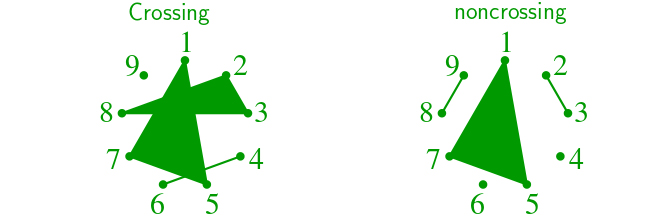
Number of noncrossing partitions of the set {1, …, 2n} in which every block is of size 2. A partition is noncrossing if and only if in its planar diagram, the blocks are disjoint (i.e. don’t cross). For example, below two are crossing and non-crossing partitions of {1, 2, 3, 4, 5, 6, 7, 8, 9}. The partition {{1, 5, 7}, {2, 3, 8}, {4, 6}, {9}} is crossing and partition {{1, 5, 7}, {2, 3}, {4}, {6}, {8, 9}} is non-crossing.
Number of Dyck words of length 2n. A Dyck word is a string consisting of n X’s and n Y’s such that no initial segment of the string has more Y’s than X’s. For example, the following are the Dyck words of length 6: XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.
Number of ways to tile a stairstep shape of height n with n rectangles. The following figure illustrates the case n = 4:
Given a number n, return the number of ways you can draw n chords in a circle with 2 x n points such that no 2 chords intersect.
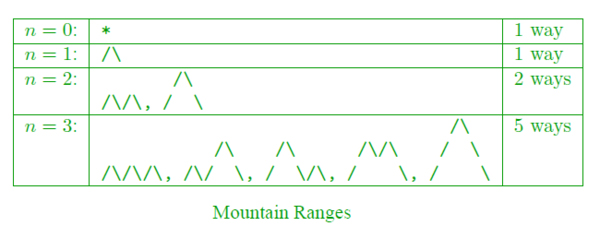
Number of ways to form a “mountain ranges” with n upstrokes and n down-strokes that all stay above the original line.The mountain range interpretation is that the mountains will never go below the horizon.
Number of stack-sortable permutations of {1, …, n}. A permutation w is called stack-sortable if S(w) = (1, …, n), where S(w) is defined recursively as follows: write w = unv where n is the largest element in w and u and v are shorter sequences, and set S(w) = S(u)S(v)n, with S being the identity for one-element sequences.
Number of permutations of {1, …, n} that avoid the pattern 123 (or any of the other patterns of length 3); that is, the number of permutations with no three-term increasing subsequence. For n = 3, these permutations are 132, 213, 231, 312 and 321. For n = 4, they are 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312 and 4321