A0-Logistic-Regression

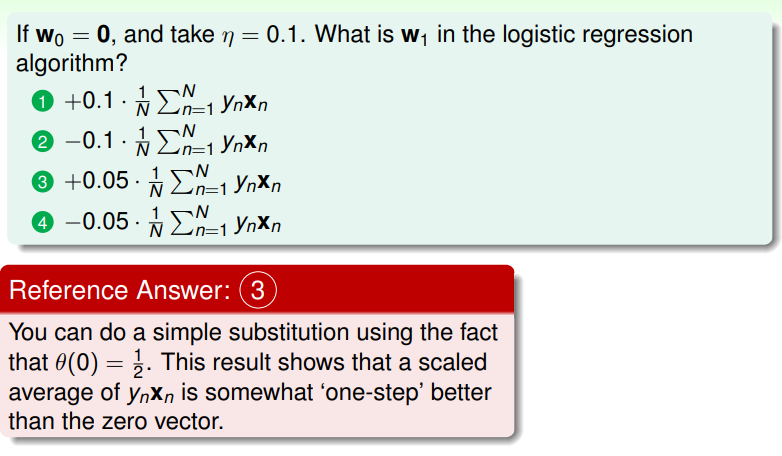
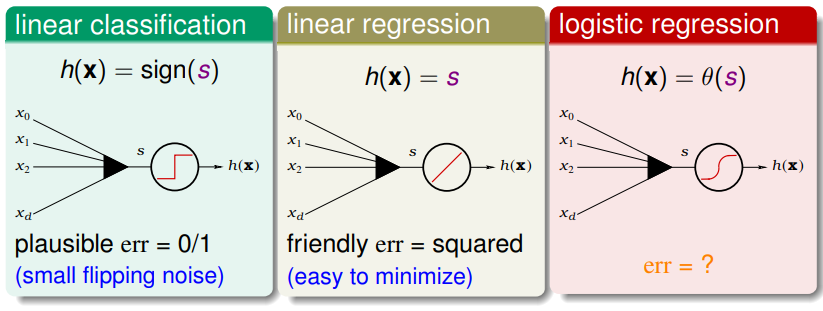
Logistic Regression Problem

考虑这样的情形：在医院中医生需要根据病人的情况，对其接下来患心脏病的概率作出预测，给出患病的概率。这种情况不是简单的二元分类，也不是线性回归，因为其输出的值是一个概率，处于 0~1 之间。

这种问题适合使用 Logistic Regression ，其学习流程如下：

• 
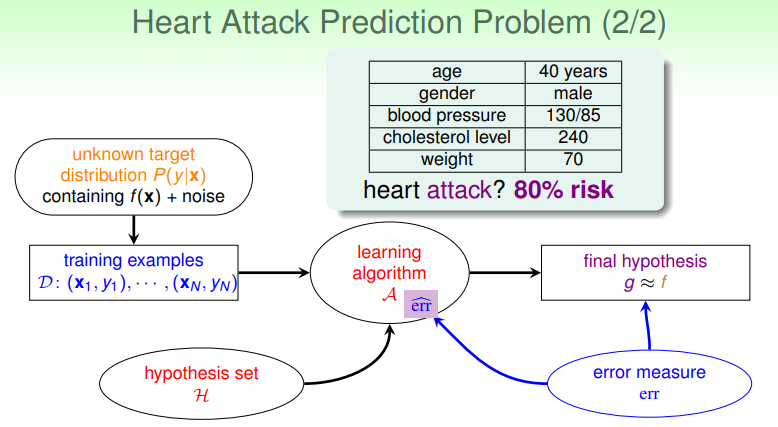
• 有时称之为“soft”二元分类，其目标函数为：$f(\mathbf{x})=P(y=+1|\mathbf{x})\in [0,1]$ ；

Why don't translate it as "逻辑回归"?

周志华西瓜书（Page 58）上指出，中文的逻辑与此处的 logistic 含义相去甚远，并且在这个算法中取对数操作占据了很重要的地位，因此建议称之为“对数几率回归”，或者干脆不译。

Feature of Data

Logistic Regression 的训练数据比较难得，因为我们无法获取以概率标好的样本，因为我们只能知道一个病人是否患了心脏病，而不是知道其患病概率：

• 
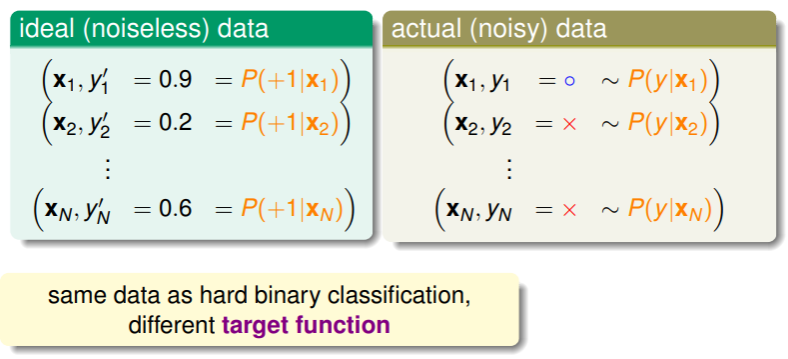
• 实际的数据是有噪音的，因为高概率患病的人实际上并不一定患病，低概率患病的人却有可能患病，这可以看作是一种服从正态分布的采样。

Logistic Function

对于 Logistic Regression ，其输入样本的特征向量为 $\mathbf{x}=(x_0,x_1,x_2,...,x_d)$ ，

• 为各维分配权重后相乘，可以得到一个分值 $s=\sum _{i=0}^d{w}_i{x}_i={\mathbf{w}}^T\mathbf{x}$ ，如果能够将结果 $s$ 映射到 $[0,1]$ 区间内，就得到了概率；
• 实现这一映射的函数称为 Logistic Function ，它的形式是 $\theta (s)=\frac{e^s}{1+e^s}=\frac{1}{1+e^{-s}}$ ，这是一个光滑的、单调递增的、S 形的（sigmoid）函数：
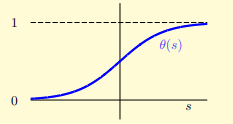
• 可以看出，这个函数在 $|s|$ 较大时变化平缓，而在 $|s|\to 0$ 时变化剧烈，函数关于 $(0,\frac{1}{2})$ 对称，因此有 $\theta (-s)=1-\theta (s)$ ；

另外，我们考虑 $1-\theta =1-\frac{1}{1+e^{-s}}=\frac{e^{-s}}{1+e^{-s}}$ ，则取对数后有 $\ln (\frac{\theta }{1-\theta })=s$ ，如果把 $\theta (\mathbf{x})$ 看作 $\mathbf{x}$ 为正例的可能性，则 $1-\theta$ 就是 $\mathbf{x}$ 为反例的可能性，$\frac{\theta }{1-\theta }$ 就是 $\mathbf{x}$ 作为正例的相对可能性，称为几率（odds），取对数后就能化为线性关系，这就是西瓜书中认为它应该叫作对数几率的由来；不过这里林老师没有提及，仅作补充了解

综合起来，我们对 Logistic Regression 的假设为 $h(\mathbf{x})=\theta ({\mathbf{w}}^T\mathbf{x})=\frac{1}{1+e^{-{\mathbf{w}}^T\mathbf{x}}}$ ，它是对目标函数 $f(\mathbf{x})=P(y=+1|\mathbf{x})$ 的近似。

练习：理解 Logistic Regression 与二元分类

Logistic Regression Error

回想一下学过的三种线性模型，它们的 scoring function 都是一样的：$s={\mathbf{w}}^T\mathbf{x}$ ，分析三者的特点我们尝试推导 Logistic Regression 的错误估计：

• 

Logistic Regression 的目标函数为 $f(\mathbf{x})=P(y=+1|\mathbf{x})$ ，写成目标分布的形式，等价于

$$P(y|\mathbf{x})=\{\begin{array}{ll}f(\mathbf{x})& \text{for }y=+1\\ 1-f(\mathbf{x})& \text{for }y=-1\end{array}$$

Cross-Entropy

考虑这样的样本数据：$\mathcal{D}=\{({\mathbf{x}}_1,\circ ),({\mathbf{x}}_2,\times ),...,({\mathbf{x}}_N,\times )\}$ ，要使用目标函数生成这样的数据，其概率（probability）为

$$P({\mathbf{x}}_1)f({\mathbf{x}}_1)\times P({\mathbf{x}}_2)(1-f({\mathbf{x}}_2))\times ...\times P({\mathbf{x}}_N)(1-f({\mathbf{x}}_N))$$

，类似的，我们的假设 $h$ 要同样生成这样的数据，其可能性（likelihood）为

$$P({\mathbf{x}}_1)h({\mathbf{x}}_1)\times P({\mathbf{x}}_2)(1-h({\mathbf{x}}_2))\times ...\times P({\mathbf{x}}_N)(1-h({\mathbf{x}}_N))$$

，因此如果假设与目标接近，那么应有

$$h\approx f⟺\text{likelihood}(h)\approx \text{probability of using }f$$

likelihood 翻译

大陆概率论课本中将 likelihood 通常翻译为“似然”。

目标函数 $f$ 是理想的，因此其产生对应样本的概率是很大的，因此最佳估计 g 应当取自所有假设中可能性最高者：$g=\underset{h}{\arg }\max \{\text{likelihood}(h)\}$ ，而对于 Logistic Regression 的假设函数 $h(\mathbf{x})=\theta ({\mathbf{w}}^T\mathbf{x})$ ，由其对称性可得：

$$\begin{array}{rl}\text{likelihood}(h)& =P({\mathbf{x}}_1)h({\mathbf{x}}_1)\times P({\mathbf{x}}_2)(1-h({\mathbf{x}}_2))\times ...P({\mathbf{x}}_N)(1-h({\mathbf{x}}_N))\\ & =P({\mathbf{x}}_1)h({\mathbf{x}}_1)\times P({\mathbf{x}}_2)h(-{\mathbf{x}}_2))\times ...P({\mathbf{x}}_N)h(-{\mathbf{x}}_N))\end{array}$$

，从而得知假设 $h$ 的可能性与假设在每个样本上的结果的连乘成正比：

$$\text{likelihood}(\text{logistic }h)\propto \prod _{n=1}^{N}h(y_n{\mathbf{x}}_n)$$

我们取所有 Logistic Regression 假设的最大者，即有

$$\underset{h}{\max }\{\text{likelihood}(\text{logistic }h)\}\propto \prod _{n=1}^{N}h(y_n{\mathbf{x}}_n)$$

，以权重向量替换其中的假设 $h$，则得到

$$\underset{\mathbf{w}}{\max }\{\text{likelihood}(\mathbf{w})\}\propto \prod _{n=1}^N\theta (y_n{\mathbf{w}}^T{\mathbf{x}}_n)$$

，对其取对数，得

$$\underset{\mathbf{w}}{\max }\{\ln \prod _{n=1}^N\theta (y_n{\mathbf{w}}^T{\mathbf{x}}_n)\}=\underset{\mathbf{w}}{\max }\sum _{n=1}^N\ln \theta (y_n{\mathbf{w}}^T{\mathbf{x}}_n)=\underset{\mathbf{w}}{\min }\sum _{n=1}^N-\ln \theta (y_n{\mathbf{w}}^T{\mathbf{x}}_n)$$

，将 $\theta (s)=\frac{1}{1+e^{-s}}$ 代入并增添一个取均值的操作（为了与之前的错误估计在形式上统一），得到

$$\underset{\mathbf{w}}{\min }\underset{E_{in}(\mathbf{w})}{\underbrace{\frac{1}{N}\sum _{n=1}^N\ln (1+e^{-y_n{\mathbf{w}}^T{\mathbf{x}}_n})}}=\underset{\mathbf{w}}{\min }\frac{1}{N}\sum _{n=1}^N\text{err}(\mathbf{w},{\mathbf{x}}_n,y_n)$$

此时，我们称 $\text{err}(\mathbf{w},\mathbf{x},y)=\ln (1+e^{-y{\mathbf{w}}^T\mathbf{x}})$ 为 cross-entropy error ，这就是 Logistic Regression 的错误估计函数。

练习：理解交叉熵错误估计

Gradient of Logistic Regression Error

接下来我们思考如何使 $E_{in}(\mathbf{w})$ 取得最小：

• 思考之前的情况，$E_{in}(\mathbf{w})$ 如果是连续、可微、凸的（矩阵的二阶导数形式如果是正定的，那么就是凸的），那么就很容易找到 $\nabla E_{in}(\mathbf{w})=0$ ，此处自然是最小值点；
• 因此对其求导：

但是，在令 $\nabla E_{in}(\mathbf{w})=0$ 时，并不像之前那么轻松：我们可以将 $\nabla E_{in}(\mathbf{w})=\frac{1}{N}\sum _{n=1}^N\theta (-y_n{\mathbf{w}}^T{\mathbf{x}}_n)(-y_n{\mathbf{x}}_n)$ 看作是对 $-y_n{\mathbf{x}}_n$ 求 $\theta -\text{weighted}$ 的加权平均，要使其为零，有两种可能：

1. 所有 $\theta (-y_n{\mathbf{w}}^T{\mathbf{x}}_n)=0$ ，回想 Logistic Function 的定义，此时相当于 $-y_n{\mathbf{w}}^T{\mathbf{x}}_n\to -\infty$ ，这意味着每个 $y_n$ 都与输入样本加权后的 ${\mathbf{w}}^T{\mathbf{x}}_n$ 是同号的，即输入样本 $\mathcal{D}$ 是线性可分的；但这种情况可遇而不可求😢
2. 所以不得不求解 $\nabla E_{in}(\mathbf{w})=0$ ，这又是一个非线性的方程，没法像线性回归那样一步登天地找到确切的解。于是，我们求助于 PLA 的思路：
   • PLA 中我们迭代地更新 ${\mathbf{w}}_t$，其规则是自 ${\mathbf{w}}_0$ 起始，每轮修正一个错误：${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t+\underset{\eta }{\underbrace{1}}\cdot \underset{\mathbf{v}}{\underbrace{([\text{sign}({\mathbf{w}}_t^T{\mathbf{x}}_n)\ne y_n]\cdot y_n{\mathbf{x}}_n)}}$ ，当不再犯错时就得到最佳近似 g ；
   • PLA 的思路是一种 iterative optimization approach ，我们下一部分讲的梯度下降法也是如此。

练习：理解样本对梯度的影响

• 最小的 $y_n{\mathbf{w}}^T{\mathbf{x}}_n$ 代表预测是错误的，而犯错在迭代式优化的方法里权重更高；

Gradient Descent

Understand Gradient

迭代式优化的步骤可以写作：${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t+\eta \mathbf{v}$ ，对于 PLA ，这里的 $\mathbf{v}$ 来自于犯错，而对 Logistic Regression ，从梯度的视角来看，相当于从山顶（或山坡的某个高度）下降到山谷：

• 
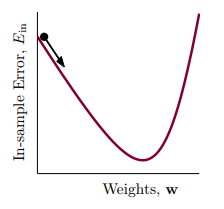
• $\mathbf{v}$ 代表着方向（单位向量），$\eta$ 代表着步长（通常为正），要找到 $E_{in}$ 的最小值，通常使用贪心策略——每一步都走到当前最低处：$\underset{||\mathbf{v}||=1}{\min }{E}_{in}({\mathbf{w}}_t+\eta \mathbf{v})$ ，
• 不过这个形式仍然不是线性的，我们可以从微元的角度——每次都走一小步，则每一小步都是线性的——来近似成线性：$E_{in}({\mathbf{w}}_t+\eta \mathbf{v})\approx E_{in}({\mathbf{w}}_t)+\eta {\mathbf{v}}^T\nabla E_{in}({\mathbf{w}}_t)$ ，这里 $\eta \to 0$ ，实际上是泰勒展开在高维中的应用；

因此最小的 $E_{in}$ 可以通过贪心策略近似地转换为线性关系：

$$\underset{||\mathbf{v}||=1}{\min }\{\underset{\text{known}}{\underbrace{E_{in}({\mathbf{w}}_t)}}+\underset{\text{given positive}}{\underbrace{\eta }}{\mathbf{v}}^T\underset{\text{known}}{\underbrace{\nabla E_{in}({\mathbf{w}}_t)}}\}$$

，要使其最小，则 $\mathbf{v}$ 与 $\nabla E_{in}({\mathbf{w}}_t)$ 方向相反，即 $\mathbf{v}=-\frac{\nabla E_{in}({\mathbf{w}}_t)}{||\nabla E_{in}({\mathbf{w}}_t)||}$ ；

综合起来，梯度下降的迭代步骤就是，对足够小的 $\eta$ ，${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t-\eta \frac{\nabla E_{in}({\mathbf{w}}_t)}{||\nabla E_{in}({\mathbf{w}}_t)||}$ ；

Fixing Learning Rate

现在来看看 $\eta$ 的取值：

• 
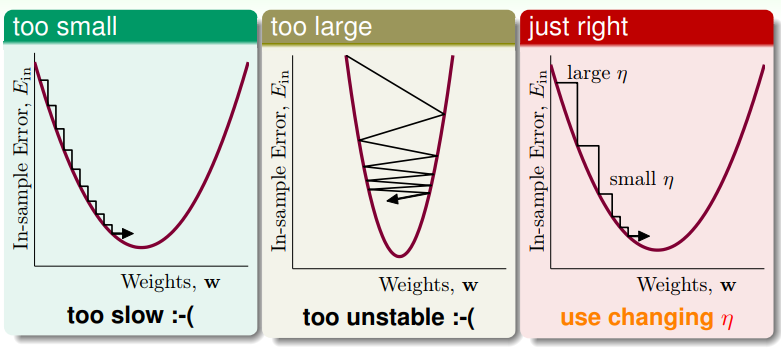
• 显然它过小时梯度下降缓慢，过大时甚至可能出错，而最佳的方法应当是在梯度大时较大，梯度小时较小，动态地变化，即与 $||\nabla E_{in}({\mathbf{w}}_t)||$ 正相关，
• 不妨记其相关比例为 ${\eta }^{{}^{\prime }}$，则有 ${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t-\eta \frac{\nabla E_{in}({\mathbf{w}}_t)}{||\nabla E_{in}({\mathbf{w}}_t)||}={\mathbf{w}}_t-{\eta }^{{}^{\prime }}\nabla E_{in}({\mathbf{w}}_t)$ ，在 ML 中 ${\eta }^{{}^{\prime }}$ 称为 fixing learning rate .

因此，完整的 Logistic Regression Algorithm 的流程是这样： 0. 初始设置一个 ${\mathbf{w}}_0$ ，每一轮迭代，都做如下步骤：

1. 计算 $\nabla E_{in}({\mathbf{w}}_t)=\frac{1}{N}\sum _{n=1}^N\theta (-y_n{\mathbf{w}}_t^T{\mathbf{x}}_n)(-y_n{\mathbf{x}}_n)$
2. 每轮通过梯度下降法 ${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t-{\eta }^{{}^{\prime }}\nabla E_{in}({\mathbf{w}}_t)$ 进行更新，直到 $\nabla E_{in}({\mathbf{w}}_{t+1})=0$ 或经历过足够多的迭代轮次
3. 返回最后的 ${\mathbf{w}}_{t+1}$ 作为最佳估计 g ；

练习：理解 Logistic Regression 的迭代