背包问题
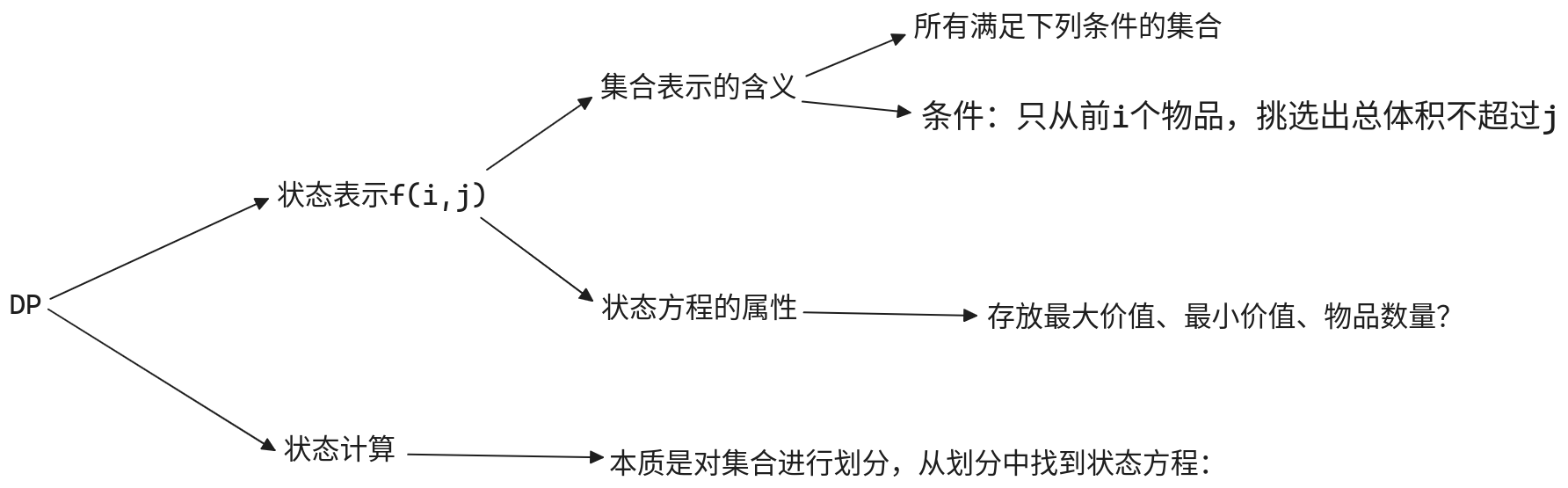
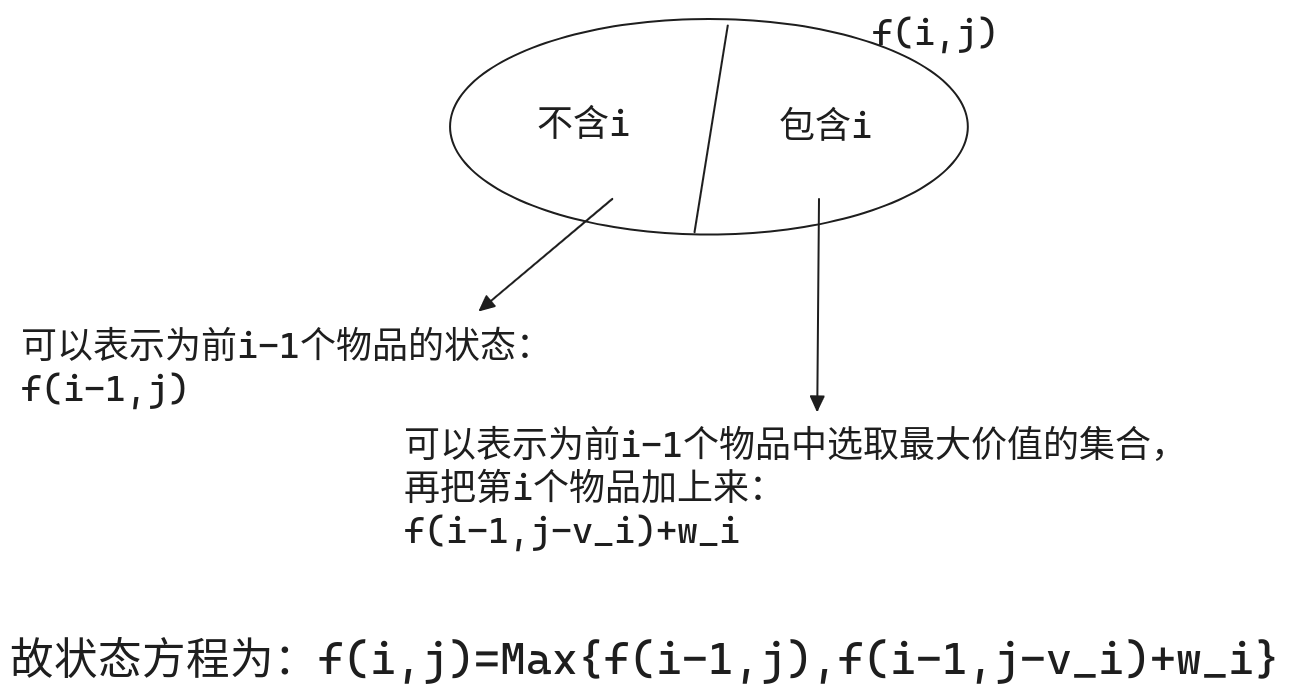
002. 0/1背包问题
// 01-knapsack
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N]; // f[i][j] 表示只看前i件物品,总体积是j的情况下,最大的总价值
int v[N], w[N]; // 记录每个物品的体积和价值
/*
result = max{f[n][0],f[n][1],f[n][2],...,f[n][V]}
计算f[i][j]:
0. f[0][0]=0 ,最开始时只有一个合法状态;(全局变量会在堆中存储,所有元素都会初始化为0)
1. 不选第i个物品,f[i][j]=f[i-1][j];
2. 选第i个物品, f[i][j]=f[i-1][j-v[i]];
3. f[i][j]=max{(1.), (2.)}
时间复杂度:O(n*V)
*/
int main() {
int num, vol;
cin >> num >> vol;
for (int i = 1; i <= num; i++)
cin >> v[i] >> w[i];
for (int i = 1; i <= num; i++)
for (int j = 0; j <= vol; j++) {
f[i][j] = f[i - 1][j];
if (j >= v[i]) // 背包体积至少要大于物品体积才可以选择
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
int res = 0;
for (int i = 0; i <= vol; i++) res = max(res, f[num][i]);
cout << res << endl;
return 0;
}DP 优化都是对基本递推方程的变形,所以一切基于基本的递推方程。上面的二阶矩阵可以考虑改用滚动数组的形式来优化:由于对 有影响的只有 ,可以去掉第一维,直接用 来表示处理到当前物品时背包容量为 的最大价值,得出以下方程::
#include <iostream>
using namespace std;
const int N = 1010;
int f[N]; // f[i] 表示总体积是i的情况下,最大的总价值
int v[N], w[N]; // 记录每个物品的体积和价值
int main() {
int num, vol;
cin >> num >> vol;
for (int i = 1; i <= num; i++)
cin >> v[i] >> w[i];
for (int i = 1; i <= num; i++)
for (int j = vol; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[vol] << endl;
return 0;
}003. 完全背包问题

// 未优化状态方程版
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N]; // f[i][j] 表示前i件物品在总体积是j的情况下,最大的总价值
int v[N], w[N]; // 记录每个物品的体积和价值
int main() {
int num, vol;
cin >> num >> vol;
for (int i = 1; i <= num; i++)
cin >> v[i] >> w[i];
for (int i = 1; i <= num; i++)
for (int j = 0; j <= vol; j++)
for (int k = 0; k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
cout << f[num][vol] << endl;
return 0;
}
// 优化状态方程版
int main() {
int num, vol;
cin >> num >> vol;
for (int i = 1; i <= num; i++)
cin >> v[i] >> w[i];
for (int i = 1; i <= num; i++)
for (int j = 0; j <= vol; j++)
if (v[i] <= j) // 第 i 种能放进去
f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
else // 如果第 i 件物品不能放进去
f[i][j] = f[i - 1][j];
cout << f[num][vol] << endl;
return 0;
}
// 再度一维数组优化版
#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i = 1 ; i <= n ;i ++)
{
cin>>v[i]>>w[i];
}
for(int i = 1 ; i<=n ;i++)
for(int j = v[i] ; j<=m ;j++)
{
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
cout<<f[m]<<endl;
}004. 多重背包问题I
数据范围:
- 物品种数与背包空间: ;
- 物品属性: ;
// 多重背包问题I
#include <iostream>
using namespace std;
const int N = 110;
int f[N][N]; // f[i][j] 表示前i件物品在总体积是j的情况下,最大的总价值
int v[N], w[N], s[N]; // 记录每个物品的体积、价值、数量
int main() {
int num, vol;
cin >> num >> vol;
for (int i = 1; i <= num; i++)
cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= num; i++)
for (int j = 0; j <= vol; j++)
for (int k = 0; k <= s[i] && k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
cout << f[num][vol] << endl;
return 0;
}005. 多重背包问题 II
数据范围:
- 物品种数与背包空间: ;
- 物品属性: ;
二进制优化 二进制优化的基本思想是将每种物品的数量进行二进制拆分,即将每种物品拆分为多个物品,每个物品的数量是 2 的幂次(1, 2, 4, …, 2^k),这样做的目的是利用二进制的特性,通过对数级别的物品数量来模拟任意数量的物品组合,从而将多重背包问题转化为 01 背包问题来求解。
#include <iostream>
#include <vector>
using namespace std;
const int N = 20010; // 根据问题规模调整N的大小
int f[N];
struct Good {
int v, w;
};
int main() {
int num, vol;
cin >> num >> vol;
vector<Good> goods;
for (int i = 1; i <= num; i++) {
int v, w, s;
cin >> v >> w >> s;
for (int k = 1; k <= s; k *= 2) { // 二进制拆分
s -= k;
goods.push_back({v * k, w * k});
}
if (s > 0) goods.push_back({v * s, w * s}); // 加入剩余的部分
}
// 01背包问题
for (auto &good : goods) {
for (int j = vol; j >= good.v; j--) {
f[j] = max(f[j], f[j - good.v] + good.w);
}
}
cout << f[vol] << endl;
return 0;
}
006. 多重背包问题 III
数据范围:
- 物品种数与背包空间: ;
- 物品属性: ;
单调队列优化 单调队列优化的多重背包问题的核心思想是,对于每种物品,使用一个单调队列来维护可能的最优解。这种方法特别适用于解决空间复杂度或时间复杂度较高的情况。单调队列可以帮助我们在 时间内得到当前窗口中的最大值,从而有效降低整个算法的时间复杂度。
- 对于每种物品,我们将它看作若干个子问题来处理,每个子问题对应物品的一部分数量。
- 对于每种物品的每个体积 ,我们考虑以 为间隔,对背包容量进行遍历,并对每个间隔内的情况使用单调队列进行优化。
- 对于给定的体积间隔,我们维护一个单调递减的队列,队列中存储的是当前体积下,选择不同数量物品时背包的价值。队列的首元素即为这个间隔内的最大价值。
- 通过队列中元素的下标差和物品的最大数量来维护队列的长度,以确保队列中的状态不会超过物品的最大数量。
// 单调队列优化 多重背包III
#include <iostream>
using namespace std;
const int N = 1010, M = 20010;
int n, m; // n是物品种数,m是背包容量
int v[N], w[N], s[N]; // v[i], w[i], s[i] 分别表示第i件物品的体积、价值和数量
int f[N][M]; // f[i][j] 表示考虑前i种物品,总体积为j时的最大价值
int q[M]; // 单调队列,用于优化DP过程
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; ++i) {
for (int r = 0; r < v[i]; ++r) { // 对于每种物品,按照余数r进行分组,确保每组中物品体积之和对v[i]取余相同
int head = 0, tail = -1; // head是队列头指针,tail是队列尾指针
for (int j = r; j <= m; j += v[i]) {
// 如果队列头部的状态已经无法转移到当前状态,则出队
while (head <= tail && j - q[head] > s[i] * v[i]) head++;
// 如果当前状态的价值不优于队尾状态的价值,则队尾状态出队
while (head <= tail && f[i - 1][q[tail]] + (j - q[tail]) / v[i] * w[i] <= f[i - 1][j]) --tail;
// 当前状态入队
q[++tail] = j;
// 计算当前状态的最优价值
f[i][j] = f[i - 1][q[head]] + (j - q[head]) / v[i] * w[i];
}
}
}
cout << f[n][m] << endl;
return 0;
}
多重背包的原始状态转移方程:
考虑用完全背包的优化方式来优化这个方程:
写出这个公式好像并不是那么管用,因为 完全背包 是一口气把所有体积全部用掉,即
然而 多重背包 对于每个物品的个数是有限制的,导致我们最终的等式是如下样子:
但是,我们可以把这个式子 继续 推导下去,直到背包体积被用到不能再用为止
其中 ,也可以理解为 完全背包 下把当前物品 选到不能再选 后,剩下的 余数。
得到 后,我们再利用 完全背包优化思路 往回倒推一遍,会惊奇的发现一个 滑动窗口求最大值 的模型,具体如下:为了方便大家观察,我们把 改写成
可能看上去还是有点复杂,为了再方便大家观察,我们去掉 w,然后把数组展开成一条链——具体如下图:

于是通过该 滑动窗口 ,我们就能在 线性 的时间里求出 i 阶段里,所有满足 的 。滑动窗口 求 最大值 的实现,只需利用 队列 在队头维护一个 最大值 的 单调递减 的 单调队列 即可。为了更新所有 i 阶段里的状态 f(i,j) ,我们只需再额外枚举所有的 余数 r 即可。
不要忘记,滑动窗口内部比较最大值的时候,有一个在之前为了方便观察,被删掉的偏移量 w ,要记得加上再比较。具体就是 当前下标 和该 最大值的下标 之间差了 个 ,那么就要加上 个 。
最后,上面朴素的优化版本的复杂度为:
- 时间复杂度: ;
- 空间复杂度: ,如果利用 01 背包问题中滚动数组的策略,还可以进一步降低到 ;
- 滑动窗口长度:
007. 混合背包问题
#include <iostream>
using namespace std;
const int N = 1010;
int f[N]; // 优化为一维数组,减少空间复杂度
int main() {
int num, vol;
cin >> num >> vol;
for (int i = 1; i <= num; i++) {
int v, w, s;
cin >> v >> w >> s;
if (s == -1) { // 01 背包
for (int j = vol; j >= v; j--)
f[j] = max(f[j], f[j - v] + w);
} else if (s == 0) { // 完全背包
for (int j = v; j <= vol; j++)
f[j] = max(f[j], f[j - v] + w);
} else { // 多重背包,使用二进制优化
if (s * v > vol) s = vol / v; // 如果物品总体积超过背包容量,则视为完全背包处理
for (int k = 1; k <= s; k *= 2) {
int mv = k * v, mw = k * w;
for (int j = vol; j >= mv; --j) {
f[j] = max(f[j], f[j - mv] + mw);
}
s -= k;
}
if (s > 0) { // 处理剩余部分,确保所有数量的物品都被考虑到
int mv = s * v, mw = s * w;
for (int j = vol; j >= mv; --j) {
f[j] = max(f[j], f[j - mv] + mw);
}
}
}
}
cout << f[vol] << endl;
return 0;
}
009. 分组背包问题
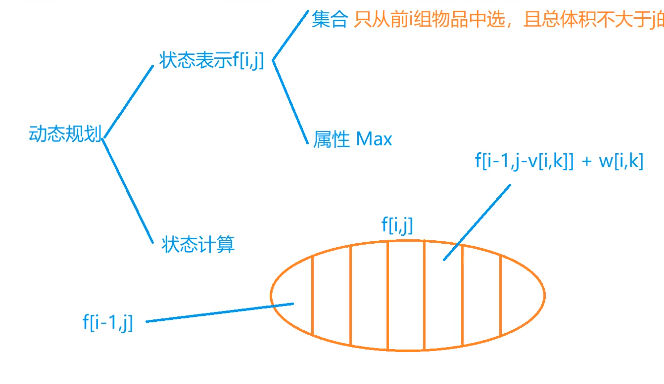
// 分组背包
#include <iostream>
using namespace std;
const int N = 110;
int f[N][N]; // 只从前i组物品中选,当前体积小于等于j的最大值
int v[N][N], w[N][N], s[N]; // v为体积,w为价值,s代表第i组物品的个数
int n, m, k;
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> s[i];
for (int j = 0; j < s[i]; j++) {
cin >> v[i][j] >> w[i][j]; // 读入
}
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j]; // 不选
for (int k = 0; k < s[i]; k++) {
if (j >= v[i][k]) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
cout << f[n][m] << endl;
}//优化版
#include<iostream>
using namespace std;
const int N=110;
int f[N];
int v[N][N],w[N][N],s[N];
int n,m,k;
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>s[i];
for(int j=0;j<s[i];j++){
cin>>v[i][j]>>w[i][j];
}
}
for(int i=0;i<n;i++){
for(int j=m;j>=0;j--){
for(int k=0;k<s[i];k++){ //for(int k=s[i];k>=1;k--)也可以
if(j>=v[i][k]) f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
cout<<f[m]<<endl;
}线性 DP
898. 数字三角形
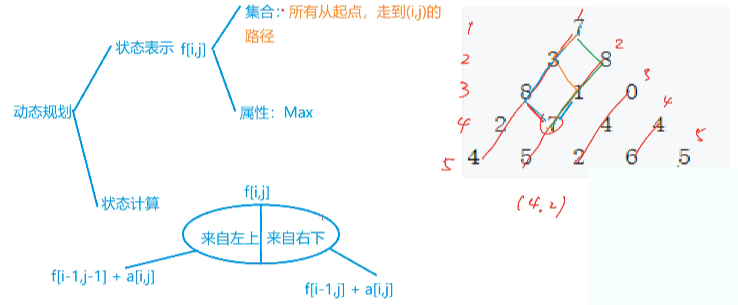
// 数字三角形
#include <iostream>
using namespace std;
const int N = 510;
int f[N][N]; // f[i][j] 表示从三角形顶部到达点(i,j)的最大路径和
/*
! [i]表示i轴坐标,(j)表示j轴坐标
[1] (1)
[2] 7 (2)
[3] 3 8 (3)
[4] 8 1 0 (4)
[5] 2 7 4 4 (5)
4 5 2 6 5
*/
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
cin >> f[i][j];
// 从三角形的倒数第二行开始向上逐行计算每个点的最大路径和
for (int i = n - 1; i >= 1; i--) // 从下往上遍历行
for (int j = 1; j <= i; j++) // 在当前行中从左到右遍历
// 更新当前点的最大路径和为:从它下方和右下方选一个较大值,再加上当前点的值
f[i][j] = max(f[i + 1][j + 1], f[i + 1][j]) + f[i][j];
// 输出从顶点到底边的最大路径和,这个值在更新后存储在f[1][1]中
cout << f[1][1] << endl;
}895. 最长上升子序列
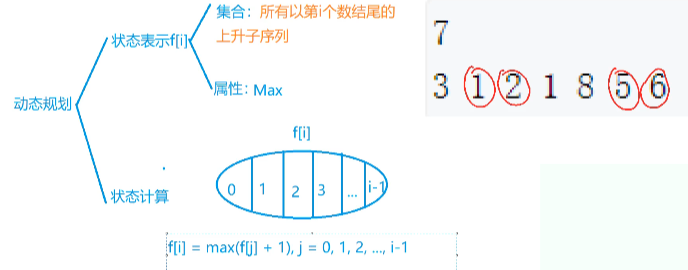
// 最长上升子序列
#include <iostream>
using namespace std;
const int N = 1010;
int f[N]; // f[i] 表示所有以第i个数结尾的(严格)上升子序列
int a[N]; // 记录输入序列
/*
3 1 2 1 8 5 6
---- ---- 故最长上升子序列的长度为4
*/
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n; i++) {
f[i] = 1; // 只有a[i]一个数
for (int j = 1; j < i; j++)
if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for (int i = 1; i <= n; i++) res = max(res, f[i]);
cout << res << endl;
}但是在数据量超过 时,上面代码的时间复杂度就会超过 1s ,从而 TLE。若要进行优化,则可以采取贪心+二分的策略将时间复杂度降低到 ,思路如下:
- 使用一个辅助数组
d[i],其中d[i]表示长度为i的所有上升子序列中末尾元素的最小值。通过维护这个数组,我们可以快速判断新的元素能被添加到哪个子序列中。 - 对于每个元素
a[i],如果它比d数组中所有元素都大,那么它可以形成一个更长的上升子序列,将其添加到d数组的末尾。 - 如果
a[i]不能添加到d数组的末尾,则通过二分查找找到d数组中第一个大于等于a[i]的元素,并用a[i]替换这个元素。这个替换保证了d数组依旧满足定义。
// 最长上升子序列II
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
const int N = 100010;
int a[N];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i];
vector<int> d(n + 1, 0);
int len = 0; // 记录当前最长上升子序列的长度
for (int i = 0; i < n; i++) {
// 通过二分查找在d中找到第一个大于等于a[i]的元素位置
int l = 1, r = len, pos = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (d[mid] < a[i]) {
pos = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
// 如果这个元素不存在,说明a[i]可以增加到d数组末尾形成更长的子序列
d[pos + 1] = a[i];
if (pos + 1 > len) len++; // 更新当前最长上升子序列的长度
}
cout << len << endl;
}
注意二分边界!
使用二分时要格外关注边界条件,比较好的办法就是坚持左闭右闭(或左闭右开)这样的限制,不要轻易改变。
897. 最长公共子序列
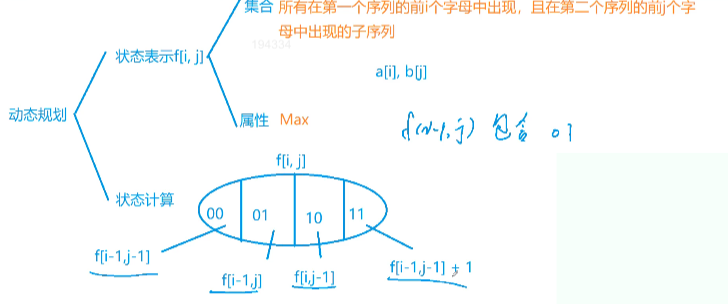
注意这里四种情况虽然有重叠,但取 Max 是没关系的,只要不漏就行。
// 最长公共子序列
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N]; // f[i][j]记录所有在第一个序列的前i个字母中出现,且在第二个序列的前j个字母中出现的子序列
char A[N], B[N];
/*
(a) c (b c)
(a b) e d (c)
*/
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> A[i];
for (int i = 1; i <= m; i++) cin >> B[i];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (A[i] == B[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
/*
f[i][j] 状态计算理解:(√ 表示选,× 表示不选)
- 00:a[i] × b[j] ×
- 01:a[i] × b[j] √
- 10:a[i] √ b[j] ×
- 11:a[i] √ b[j] √
1. 单独考虑 11:if (a[i] == b[j]) f[i - 1][j - 1] + 1
2. 考虑组合 00 && 01:a[i] × b[j] √/×(可选可不选) f[i - 1][j]
3. 考虑组合 00 && 10:a[i] √/×(可选可不选)b[j] × f[i][j - 1]
*/
cout << f[n][m] << endl;
}
902. 最短编辑距离
// 最短编辑距离
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N]; // f[i][j]记录从前一个序列的前i个字符转换为第二个序列的前j个字符所需要的最少操作次数
char A[N], B[N];
int n, m;
/*
AA T G 增、改操作共4次
AGTCTG ACGC
AGTAAGTAGGC
*/
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> A[i];
cin >> m;
for (int i = 1; i <= m; i++) cin >> B[i];
//* 另一些更简洁的输入方法
// scanf("%d%s", &n, A + 1); // 输入字符串A
// scanf("%d%s", &m, B + 1); // 输入字符串B
//
// cin >> n >> a + 1 >> m >> b + 1; (这个也可以)
// 初始化操作数的边界情况
for (int i = 0; i <= m; i++) f[0][i] = i; // 从空字符串变到B的前i个字符需要i次插入操作
for (int i = 0; i <= n; i++) f[i][0] = i; // 从A的前i个字符串变为空字符串需要i次删除操作
// for (int i = 1; i <= max(n, m); i ++) f[0][i] = f[i][0] = i;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1); // 分别对应删除A的一个字符或在A中插入B的一个字符
if (A[i] == B[j])
f[i][j] = min(f[i][j], f[i - 1][j - 1]); // 如果当前字符相同,则不需要额外操作
else
f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1); // 否则进行替换
}
cout << f[n][m] << endl;
return 0;
}
f[0][i]和f[i][0]的初始化是基于编辑距离的边界情况:即一个字符串变换到另一个字符串的最少操作次数,当其中一个字符串长度为0时,操作次数等于另一个字符串的长度。- 对于每一对
(i, j),我们都计算将a[1...i]转换为b[1...j]的最小操作数。有三种情况:- 删除操作:如果最后一个操作是删除
a[i],则问题转换为将a[1...i-1]转换为b[1...j],对应的状态是f[i - 1][j] + 1。 - 插入操作:如果最后一个操作是在
a[1...i]中插入b[j]以匹配b[j],则问题转换为将a[1...i]转换为b[1...j-1],对应的状态是f[i][j - 1] + 1。 - 替换或匹配操作:如果
a[i]和b[j]相等,不需要操作,状态转移到f[i-1][j-1];如果不等,则需要将a[i]替换成b[j],对应的状态是f[i - 1][j - 1] + 1。
- 删除操作:如果最后一个操作是删除
- 动态规划过程中,我们不断更新
f[i][j]的值,直到遍历完所有的字符。最终,f[n][m]就是将整个字符串A转换成B所需的最少操作次数。
899. 编辑距离
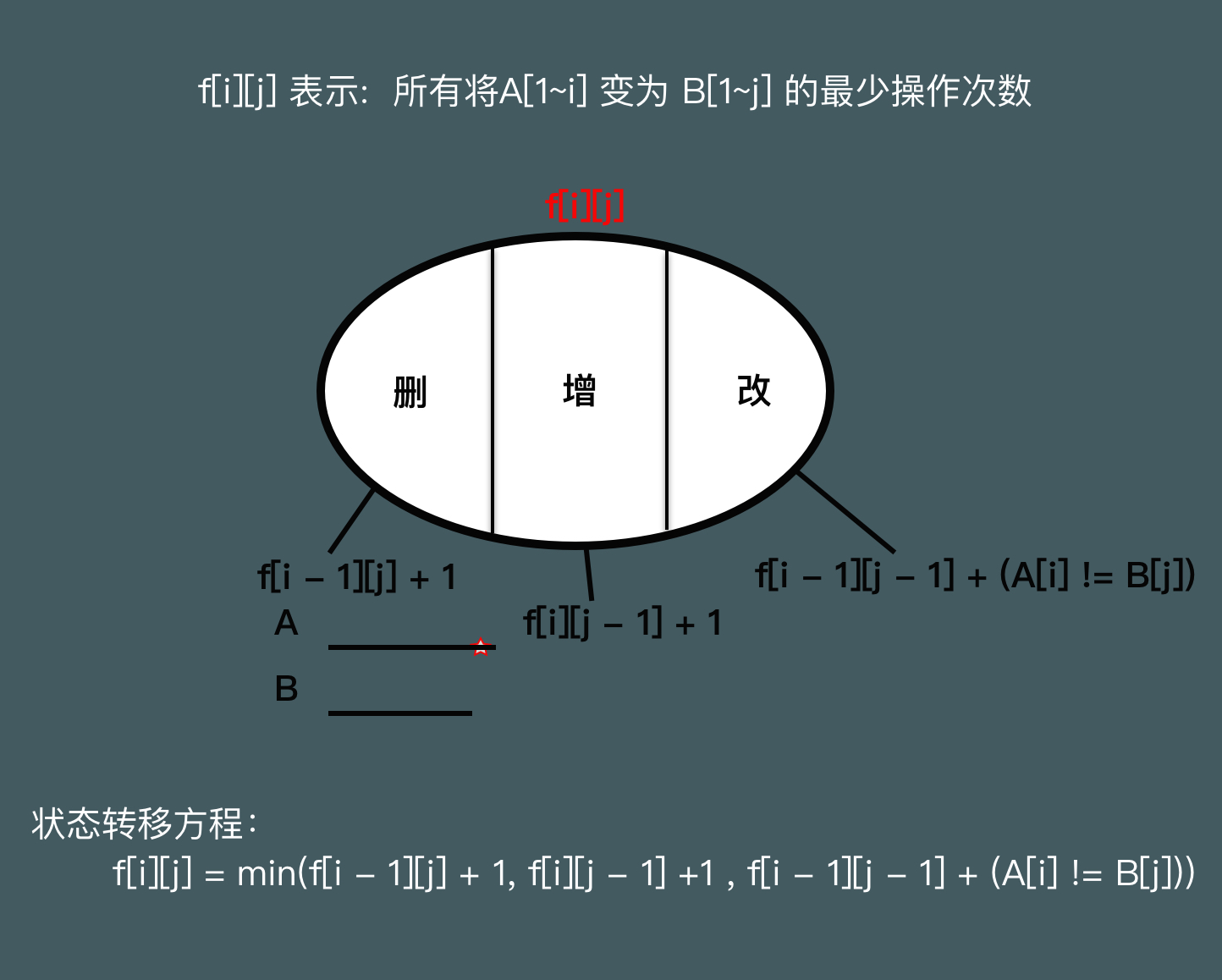
// 编辑距离
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1e1 + 5, M = 1e3 + 10; // N是字符串的最大长度+5,M是字符串的最大数量+10
int n, m; // n是给定字符串的数量,m是查询的数量
char str[M][N]; // 存储给定的字符串
int f[N][N]; // 动态规划表,f[i][j]表示字符串a的前i个字符到字符串b的前j个字符的最小编辑距离
// 计算两个字符串a和b之间的编辑距离
int edit_distance(char a[], char b[]) {
int la = strlen(a + 1), lb = strlen(b + 1); // 计算字符串a和b的长度
// 初始化边界情况
for (int i = 0; i <= lb; i++) {
f[0][i] = i; // a为空字符串时,将b转换成a需要的操作数等于b的长度
}
for (int i = 0; i <= la; i++) {
f[i][0] = i; // b为空字符串时,将a转换成b需要的操作数等于a的长度
}
// 动态规划计算编辑距离
for (int i = 1; i <= la; i++) {
for (int j = 1; j <= lb; j++) {
// 计算删除、插入和替换操作中的最小值
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1); // 分别对应于删除和插入操作
f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j])); // 对应于替换操作或者字符匹配时无需操作
}
}
return f[la][lb]; // 返回两个字符串的最小编辑距离
}
int main() {
cin >> n >> m; // 输入字符串数量和查询数量
for (int i = 0; i < n; i++) {
cin >> (str[i] + 1); // 读取每个字符串
}
while (m--) { // 对每个查询进行处理
int res = 0; // 记录满足条件的字符串数量
char s[N]; // 查询的目标字符串
int limit; // 编辑距离的限制
cin >> (s + 1) >> limit; // 读取目标字符串和编辑距离限制
for (int i = 0; i < n; i++) {
// 对每个给定的字符串计算与目标字符串的编辑距离
if (edit_distance(str[i], s) <= limit) {
res++; // 如果编辑距离小于等于限制,则计数器加一
}
}
cout << res << endl; // 输出满足条件的字符串数量
}
return 0;
}
- 初始化
f[0][i]和f[i][0]分别表示将空字符串转换为另一个字符串(或相反)需要的编辑次数,即字符串的长度。 - 通过双层循环计算任意两个字符串之间的编辑距离。对于每对位置
(i, j),考虑插入、删除或替换操作,选择最小的编辑次数。 - 对于每个查询,计算目标字符串与给定字符串数组中每个字符串的编辑距离,统计满足编辑距离限制的字符串数量。
- 动态规划表
f[i][j]的核心是递推关系:考虑当前字符匹配或不匹配的情况,从而决定是直接从前一个状态转移过来,还是通过一次编辑操作(插入、删除、替换)转移过来。
区间 DP
282. 石子合并
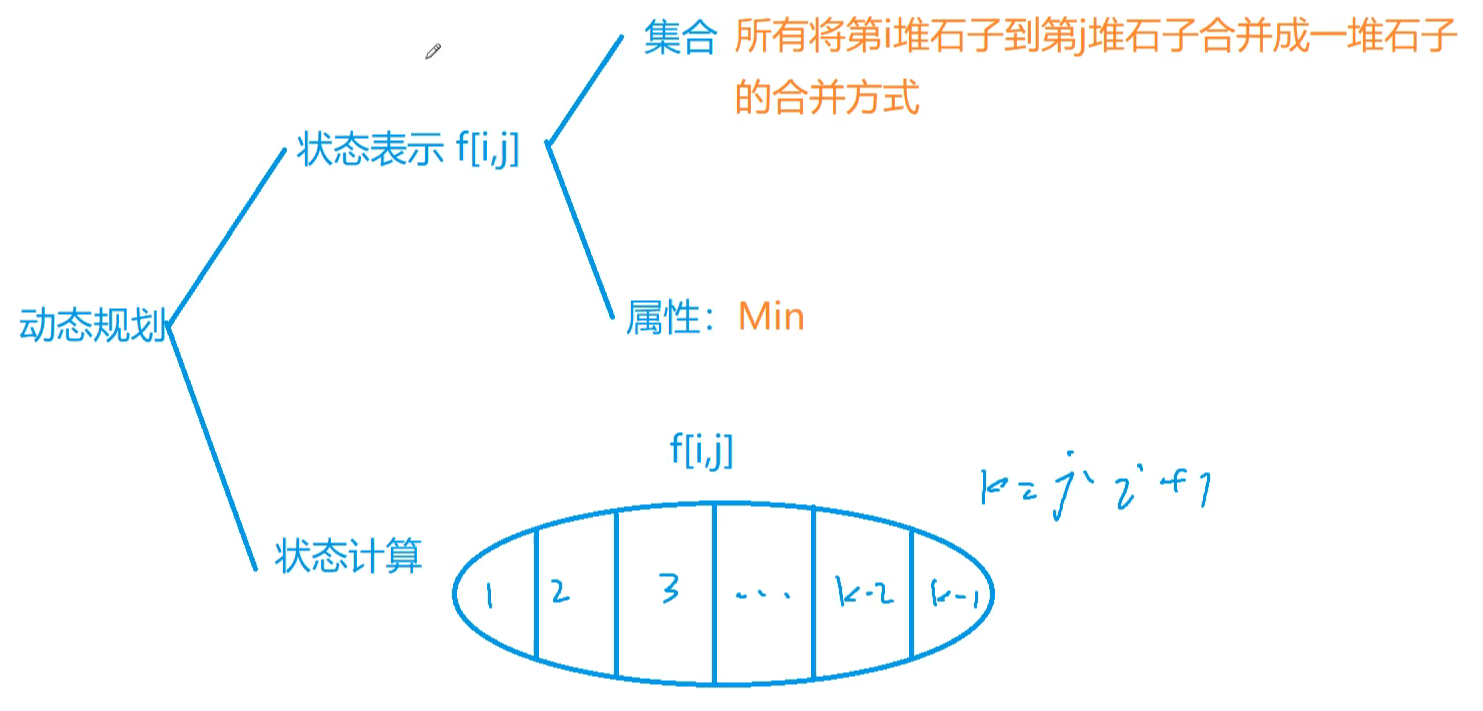
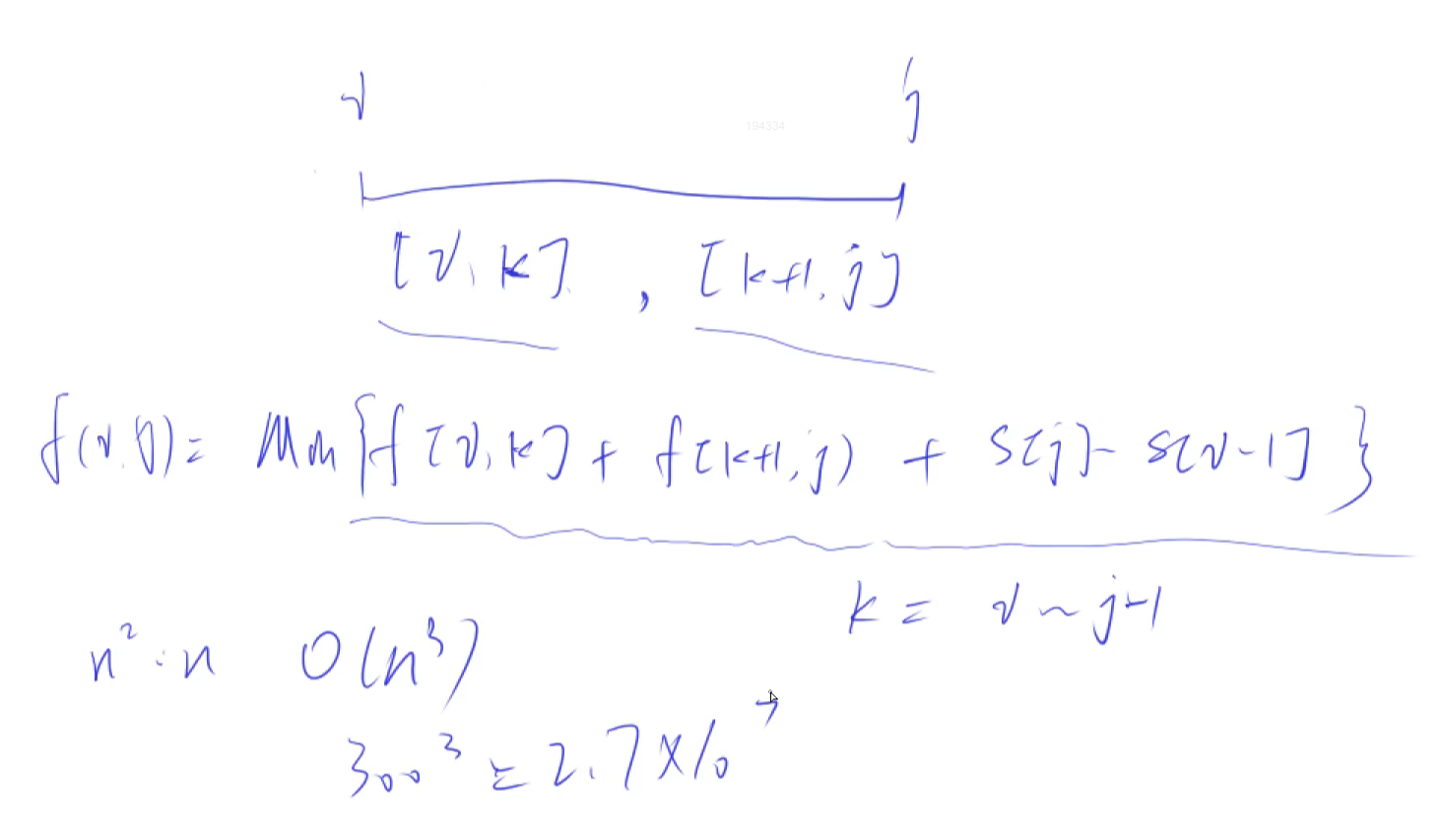
// 石子合并
#include <iostream>
using namespace std;
const int N = 310, INF = 1e9;
int f[N][N]; // f[i][j] 表示所有将第i堆石子到第j堆石子进行合并的最小代价
int w[N]; // 记录石子的重量
int s[N]; // 记录石子重量的前缀和
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> w[i];
s[i] = s[i - 1] + w[i];
}
// 初始化DP数组为INF
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
f[i][j] = (i == j) ? 0 : INF;
// 区间DP计算
for (int len = 2; len <= n; len++) { // 枚举区间长度
for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
int j = i + len - 1; // 计算终点
for (int k = i; k < j; k++) // 枚举分割点
f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
}
}
cout << f[1][n] << endl;
return 0;
}- 我们先计算所有子问题的答案,即所有可能的
[i, j]区间合并的最小代价,然后根据这些子问题的答案来计算更大区间的答案。 - 通过前缀和数组
s,我们可以快速计算出任意区间[i, j]内所有石子的总重量,即s[j] - s[i - 1]。 - 初始化时,将所有的
f[i][j]设为INF,除了当i == j时,此时没有石子需要合并,代价为0。 - 通过外层循环枚举区间长度,内层循环枚举区间起点,再通过一个内嵌循环枚举区间内的分割点,来更新
f[i][j]的值。
计数类 DP
900. 整数划分
// 整数划分
#include <iostream>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int f[N][N]; // f[i][j] 表示只从1~i中选取,且总和等于j的方案数
int main() {
int n;
cin >> n;
// 初始化:没有整数组成总和为0的方案数为1
for (int i = 0; i <= n; i++) {
f[i][0] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
// 如果当前整数i可以放入总和为j的方案中
if (j >= i) {
// 方案可以是不使用i的方案数f[i-1][j],加上使用i时的方案数f[i][j-i]
f[i][j] = (f[i - 1][j] + f[i][j - i]) % mod;
} else {
// 如果i太大,不能放入总和为j的方案,方案数与上一个整数i-1时相同
f[i][j] = f[i - 1][j];
}
}
}
cout << f[n][n];
return 0;
}- 初始化:我们初始化
f[i][0] = 1,表示对于任何i,总和为0的方案只有一种,即不选择任何数字。 - 状态转移:对于状态
f[i][j],如果选择当前的整数i作为划分的一部分(即j >= i),则方案数为两部分之和:f[i - 1][j]:不包含当前整数i的方案数。f[i][j - i]:包含至少一个当前整数i,且总和减去i后的方案数。
- 最终结果:
f[n][n]即为使用1到n的整数组成总和为n的所有方案数。
// 优化为一维数组
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N];
int main()
{
cin >> n;
f[0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j ++ )
f[j] = (f[j] + f[j - i]) % mod;
cout << f[n] << endl;
return 0;
}
// 状态转移方程:f[i][j] = f[i - 1][j] + f[i][j - i]数位统计 DP
338. 计数问题
// 计数问题
#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int N = 10;
/*
001~abc-1, 999
abc
1. num[i] < x, 0
2. num[i] == x, 0~efg
3. num[i] > x, 0~999
*/
int get(vector<int> num, int l, int r) { // 因为我们举的分类中,有需要求出一串数字中某个区间的数字,例如abcdefg有一个分类需要求出efg+1
int res = 0;
for (int i = l; i >= r; i--) res = res * 10 + num[i]; // 这里从小到大枚举是因为下面count的时候读入数据是从最低位读到最高位,那么此时在num里,最高位存的就是数字的最低位,那么假如我们要求efg,那就是从2算到0
return res;
}
int power10(int i) { // 这里有power10是因为有一个分类需要求得十次方的值,例如abc*10^3
int res = 1;
while (i--) res *= 10;
return res;
}
int count(int n, int x) {
if (!n) return 0;
vector<int> num; // num存储数中每一位的数字
while (n) {
num.push_back(n % 10);
n /= 10;
}
n = num.size(); // 长度
int res = 0;
for (int i = n - 1 - !x; i >= 0; i--) // 这里需要注意,我们的长度需要减一,是因为num是从0开始存储,而长度是元素的个数,因此需要减1才能读到正确的数值,而!x出现的原因是因为我们不能让前导零出现,如果此时需要我们列举的是0出现的次数,那么我们自然不能让他出现在第一位,而是从第二位开始枚举
{
if (i < n - 1) // 其实这里可以不用if判断,因为for里面实际上就已经达成了if的判断,但为了方便理解还是加上if来理解,这里i要小于n-1的原因是因为我们不能越界只有7位数就最高从七位数开始读起
{
res += get(num, n - 1, i + 1) * power10(i); // 这里就是第一个分类,000~abc-1,那么此时情况个数就会是abc*10^3,这里的3取决于后面efg的长度,假如他是efgh,那么就是4
// 这里的n-1,i-1,自己将数组列出来然后根据分类标准就可以得出为什么l是n-1,r是i-1
if (!x) res -= power10(i); // 假如此时我们要列举的是0出现的次数,因为不能出现前导零,这样是不合法也不符合我们的分类情况,例如abcdefg我们列举d,那么他就得从001~abc-1,这样就不会直接到efg,而是会到0efg,因为前面不是前导零,自然就可以列举这个时候0出现的次数,所以要减掉1个power10
}
// 剩下的这两个就直接根据分类标准来就好了
if (num[i] == x)
res += get(num, i - 1, 0) + 1;
else if (num[i] > x)
res += power10(i);
}
return res; // 返回res,即出现次数
}
int main() {
int a, b;
while (cin >> a >> b, a) // 读入数据,无论a,b谁是0,都是终止输入,因为不会有数字从零开始(a,b>0)
{
if (a > b) swap(a, b); // 因为我们需要从小到大,因此如果a大于b,那么就得交换,使得a小于b
for (int i = 0; i <= 9; i++) // 列举a和b之间的所有数字中 0∼9的出现次数
cout << count(b, i) - count(a - 1, i) << ' '; // 这里有点类似前缀和,要求a和b之间,那么就先求0到a i出现的次数,再求0到b i出现的次数,最后再相减就可以得出a和b之间i出现的次数
cout << endl;
}
return 0;
}状态压缩 DP
291. 蒙德里安的梦想
题意重述:给定 的方格,看能分成多少个 的小方块。
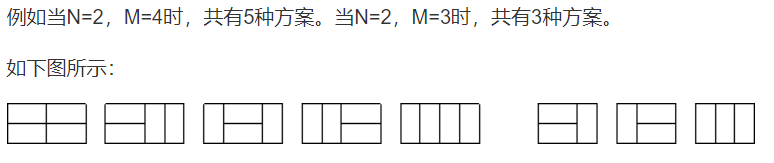
题目分析:
- 摆放方块的时候,先放横着的,再放竖着的。总方案数等于只放横着的小方块的合法方案数。
- 如何判断当前方案数是否合法?所有剩余位置能否填充满竖着的小方块。可以按列来看,每一列内部所有连续的空着的小方块需要是偶数个。
- 这是一道动态规划的题目,并且是一道 状态压缩 dp:用一个 N 位的二进制数,每一位表示一个物品,0/1 表示不同的状态。因此可以用 ( N 二 进 制 对 应 的 十 进 制 数 )中的所有数来枚举全部的状态。
状态表示:
f[i][j]表示已经将前 i -1 列摆好,且从第i-1列,伸出到第i列的状态是j的所有方案。其中j是一个二进制数,用来表示哪一行的小方块是横着放的,其位数和棋盘的行数一致:
- 上图中
i=2, j=10101(二进制数,但是存的时候用十进制) 所以这里的f[i] [j]表示的是所有前i列摆完之后,从第i-1列伸到 第i列的状态是 10101(第 1 行伸出来,第 3 行伸出来,第 5 行伸出来,其他行没伸出来)的方案数。
状态转移:
- 既然第 i 列固定了,我们需要看 第 i-2 列是怎么转移到到第 i-1 列的(看最后转移过来的状态)。假设此时对应的状态是 k(第 i-2 列到第 i-1 列伸出来的二进制数,比如 00100),k 也是一个二进制数,1 表示哪几行小方块是横着伸出来的,0 表示哪几行不是横着伸出来的。
- 它对应的方案数是
f[i-1, k],即前 i-2 列都已摆完,且从第 i-2 列伸到第 i-1 列的状态为 k 的所有方案数。 - 这个 k 需要满足什么条件呢?
- 首先 k 不能和 j 在同一行(如下图):因为从 i-1 列到第 i 列是横着摆放的
1*2的方块,那么 i-2 列到 i-1 列就不能是横着摆放的,否则就是1*3的方块了!这与题意矛盾。所以 k 和 j 不能位于同一行。 - 既然不能同一行伸出来,那么对应的代码为
(k & j ) ==0,表示两个数相与,如果有 1 位相同结果就不是 0,(k & j ) ==0表示 k 和 j 没有 1 位相同, 即没有 1 行有冲突。 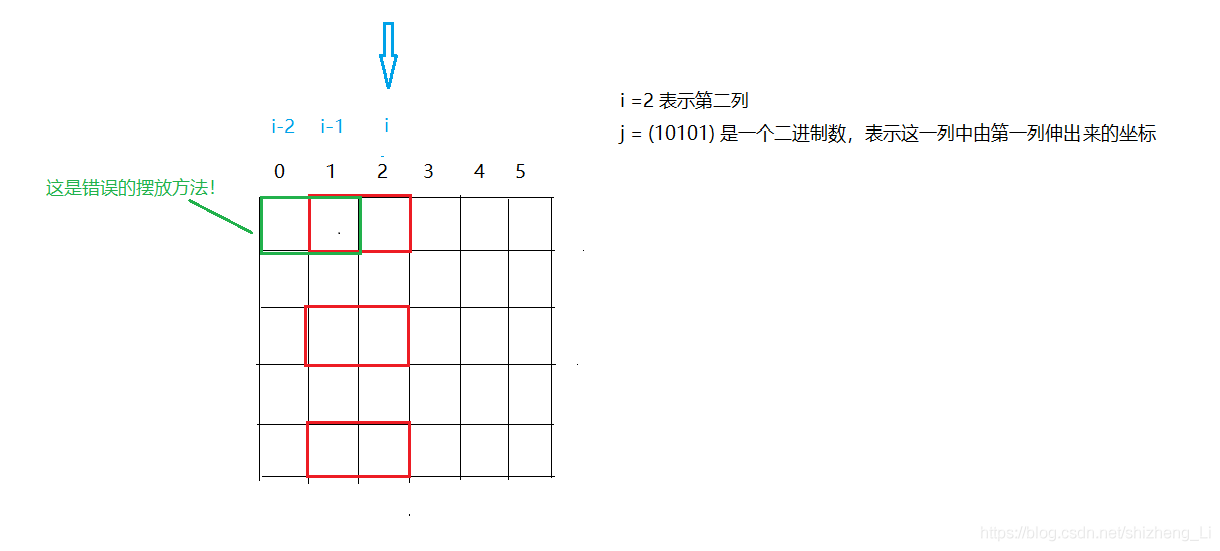
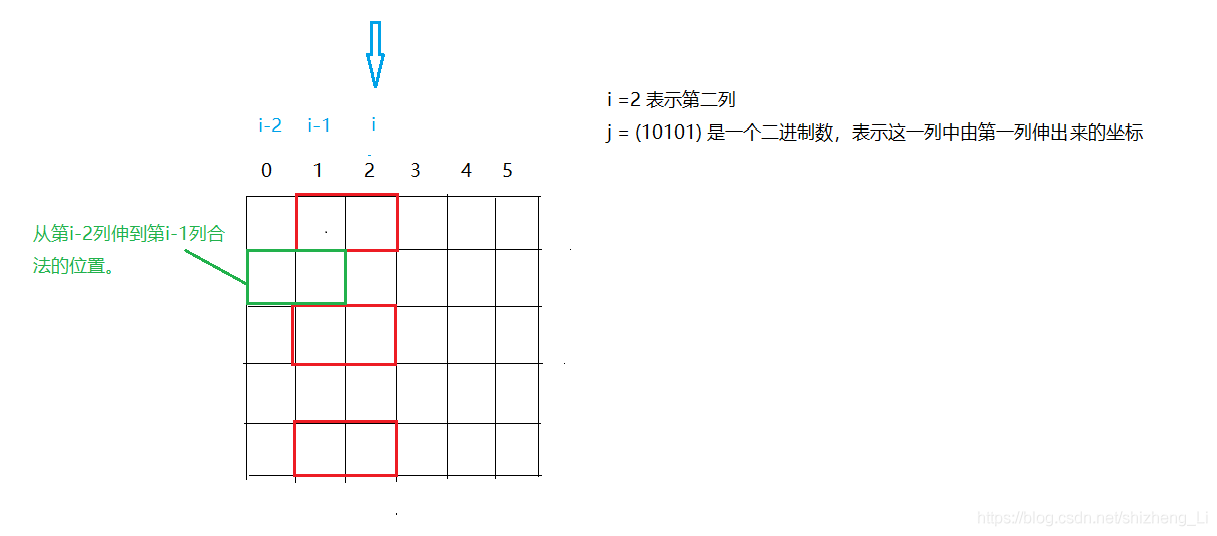
- 首先 k 不能和 j 在同一行(如下图):因为从 i-1 列到第 i 列是横着摆放的
- 既然从第 i-1 列到第 i 列横着摆的,和第 i-2 列到第 i-1 列横着摆的都确定了,那么第 i-1 列 空着的格子就确定了,这些空着的格子将来用作竖着放。如果 某一列有这些空着的位置,那么该列所有连续的空着的位置长度必须是偶数。
- 总共 m 列,我们假设列下标从 0 开始,即第 0 列,第 1 列……,第 m-1 列。根据状态表示
f[i][j]的定义,我们答案是什么呢? 请读者返回定义处思考一下。答案是f[m][0], 意思是 前 m-1 列全部摆好, 且从第 m-1 列到 m 列状态是 0(意即从第 m-1 列到第 m 列没有伸出来的)的所有方案,即整个棋盘全部摆好的方案。
dp 的时间复杂度 = 状态表示 × 状态转移
- 状态表示
f[i][j]第一维 i 可取 11,第二维 j(二进制数)可取 ,所以状态表示 , - 状态转移 也是 ,
- 所以总的时间复杂度 ,故可以过。
// 蒙德里安的梦想
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int N = 12, M = 1 << N;
long long f[N][M]; // 第一维表示列, 第二维表示所有可能的状态
bool st[M]; // 存储每种状态是否有奇数个连续的0,如果奇数个0是无效状态,如果是偶数个零置为true。
vector<vector<int>> state(M); // 二维数组记录合法的状态
int m, n;
int main() {
while (cin >> n >> m, n || m) { // 读入n和m,并且不是两个0即合法输入就继续读入
// 第一部分:预处理1
// 对于每种状态,先预处理每列不能有奇数个连续的0
for (int i = 0; i < (1 << n); i++) {
int cnt = 0; // 记录连续的0的个数
bool isValid = true; // 某种状态没有奇数个连续的0则标记为true
for (int j = 0; j < n; j++) { // 遍历这一列,从上到下
if ((i >> j) & 1) {
// i >> j位运算,表示i(i在此处是一种状态)的二进制数的第j位;
// &1为判断该位是否为1,如果为1进入if
if (cnt & 1) {
// 这一位为1,看前面连续的0的个数,如果是奇数(cnt &1为真)则该状态不合法
isValid = false;
break;
}
cnt = 0; // 既然该位是1,并且前面不是奇数个0(经过上面的if判断),计数器清零。
// 其实清不清零没有影响
} else
cnt++; // 否则的话该位还是0,则统计连续0的计数器++。
}
if (cnt & 1) isValid = false; // 最下面的那一段判断一下连续的0的个数
st[i] = isValid; // 状态i是否有奇数个连续的0的情况,输入到数组st中
}
// 第二部分:预处理2
// 经过上面每种状态 连续0的判断,已经筛掉一些状态。
// 下面来看进一步的判断:看第i-2列伸出来的和第i-1列伸出去的是否冲突
for (int j = 0; j < (1 << n); j++) { // 对于第i列的所有状态
state[j].clear(); // 清空上次操作遗留的状态,防止影响本次状态。
for (int k = 0; k < (1 << n); k++) { // 对于第i-1列所有状态
if ((j & k) == 0 && st[j | k])
// 第i-2列伸出来的 和第i-1列伸出来的不冲突(不在同一行)
// 解释一下st[j | k]
// 已经知道st[]数组表示的是这一列没有连续奇数个0的情况,
// 我们要考虑的是第i-1列(第i-1列是这里的主体)中从第i-2列横插过来的,
// 还要考虑自己这一列(i-1列)横插到第i列的
// 比如 第i-2列插过来的是k=10101,第i-1列插出去到第i列的是 j =01000,
// 那么合在第i-1列,到底有多少个1呢?
// 自然想到的就是这两个操作共同的结果:两个状态或。 j | k = 01000 | 10101 = 11101
// 这个 j|k 就是当前 第i-1列的到底有几个1,即哪几行是横着放格子的
state[j].push_back(k);
// 二维数组state[j]表示第j行,
// j表示 第i列“真正”可行的状态,
// 如果第i-1列的状态k和j不冲突则压入state数组中的第j行。
// “真正”可行是指:既没有前后两列伸进伸出的冲突;又没有连续奇数个0。
}
}
// 第三部分:dp开始
memset(f, 0, sizeof f);
// 全部初始化为0,因为是连续读入,这里是一个清空操作。
// 类似上面的state[j].clear()
f[0][0] = 1; // 这里需要回忆状态表示的定义
// 按定义这里是:前第-1列都摆好,且从-1列到第0列伸出来的状态为0的方案数。
// 首先,这里没有-1列,最少也是0列。
// 其次,没有伸出来,即没有横着摆的。即这里第0列只有竖着摆这1种状态。
for (int i = 1; i <= m; i++) { // 遍历每一列:第i列合法范围是(0~m-1列)
for (int j = 0; j < (1 << n); j++) { // 遍历当前列(第i列)所有状态j
for (auto k : state[j]) // 遍历第i-1列的状态k,如果“真正”可行,就转移
f[i][j] += f[i - 1][k]; // 当前列的方案数就等于之前的第i-1列所有状态k的累加。
}
}
// 最后答案是什么呢?
// f[m][0]表示 前m-1列都处理完,并且第m-1列没有伸出来的所有方案数。
// 即整个棋盘处理完的方案数
cout << f[m][0] << endl;
}
}
91. 最短Hamilton路径
- In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once.
- A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex exactly once.
- A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path.
- The computational problems of determining whether such paths and cycles exist in graphs are NP-complete.
倒数第二个点做分类
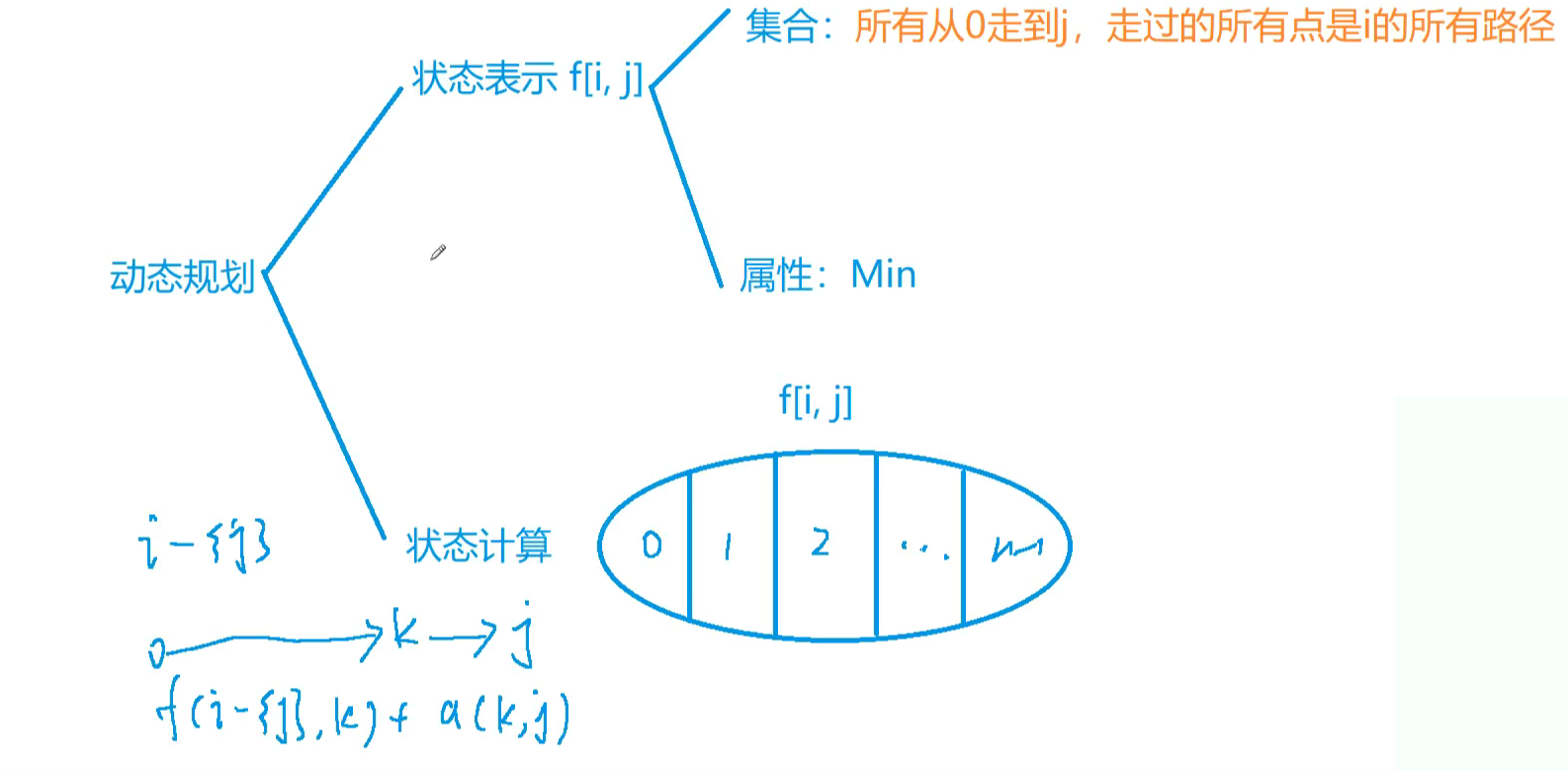
这里如何利用状态压缩?
状态压缩DP利用位运算来高效地表示一个集合(这里是已访问顶点的集合),主要利用的是二进制数的每一位代表集合中的一个元素是否存在。比如,对于五个顶点的图,二进制数
10101表示顶点0、2、4已经被访问过。在这个问题中,我们通过二进制数来表示已访问顶点的集合,用
1 << i(即2^i)表示只访问了顶点i的集合,利用这个特性,我们可以通过位运算符来高效地执行集合的并、交和差操作。
// 最短Hamilton路径
#include <iostream>
using namespace std;
const int N = 20, M = 1 << N, INF = 0x3f3f3f3f;
int f[M][N]; // f[i][j] 表示访问过的顶点集合为i,且最后到达顶点j的最短路径长度
int a[N][N]; // a[i][j] 表示i-->j之间的距离,数据保证a[i][i]==0(稠密图的邻接矩阵表示)
int n;
int main() {
cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) cin >> a[i][j];
// 初始化DP数组为无穷大,除了f[1][0],表示只访问过起点0的情况,路径长度为0
fill(f[0], f[0] + M * N, INF);
f[1][0] = 0;
// 遍历所有状态,i表示状态,即访问过的顶点集合
for (int i = 1; i < 1 << n; i += 2) // 所有方案的0号位都为1,因此递增步长为2可以避免考虑0号位为0的情况
for (int j = 0; j < n; j++) // 枚举最后到达的顶点j
if (i >> j & 1) // 如果状态i中包含顶点j
for (int k = 0; k < n; k++) // 枚举倒数第二个到达的顶点k
if (i >> k & 1) // 如果状态i中包含顶点k
// 更新状态。从状态i中去除顶点j,加上从k到j的距离
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + a[k][j]);
// 输出从0号顶点出发,访问所有顶点恰好一次,并回到起点0的最短路径长度
cout << f[(1 << n) - 1][n - 1] << endl;
return 0;
}-
f[M][N]数组:M代表所有可能的顶点集合状态(由于是二进制表示,所以M = 1 << N),N代表顶点的个数。f[i][j]存储了顶点集合为i时,以顶点j结尾的所有路径中的最短路径长度。 -
初始化:
f[1][0]初始化为0,因为从顶点0出发,访问顶点集合只有0自己时的最短路径长度显然是0。其他情况初始化为INF,表示极大值。 -
外层循环
i:遍历所有的状态,即所有可能的顶点集合。因为我们总是从顶点0开始,所以状态的最低位总是1,表示顶点0已经被访问过了,故i从1开始且每次递增2,跳过了最低位为0的无效状态。 -
内层循环
j:尝试将状态i的最后到达的顶点设为j,并根据此来更新f[i][j]的值。 -
最内层循环
k:考虑所有可能的倒数第二个到达的顶点k,并基于此来更新f[i][j]的值。这里使用i - (1 << j)表示从状态i中去除顶点j后的状态,然后从该状态转移到新状态i(包括顶点j),且最后到达顶点j的最短路径长度。 -
结果输出:输出在所有顶点都被访问的情况下(
i = (1 << n) - 1),以顶点n - 1结尾的最短路径长度,即f[(1 << n) - 1][n - 1]。
// 递归法,但是时间复杂度极高,n=15时用时超过1min都解不出来
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int N = 25, INF = 0x3f3f3f3f;
int a[N][N];
bool visited[N]; // 标记数组,记录每个顶点是否被访问过
int n;
int res = INF; // 记录最短路径的长度
// DFS函数,参数:当前顶点u,当前路径长度len,已访问顶点数count
void dfs(int u, int len, int count) {
if (count == n) { // 如果已访问所有顶点
if (u == n - 1) { // 并且当前顶点是终点
res = min(res, len); // 更新最短路径长度
}
return;
}
for (int v = 0; v < n; v++) { // 遍历所有顶点
if (!visited[v]) { // 如果顶点v未被访问
visited[v] = true; // 标记顶点v为已访问
dfs(v, len + a[u][v], count + 1); // 递归访问顶点v
visited[v] = false; // 回溯,恢复顶点v的未访问状态
}
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> a[i][j];
}
}
memset(visited, false, sizeof(visited)); // 初始化visited数组
visited[0] = true; // 从0号点出发
dfs(0, 0, 1); // 从0号点开始DFS搜索,当前路径长度为0,已访问顶点数为1
cout << res << endl; // 输出最短路径的长度
return 0;
}
- 递归+回溯方法的时间复杂度:对于递归方法,最坏情况下的时间复杂度接近于全排列,即 ,其中
n是顶点的数量。这是因为在没有有效剪枝的情况下,你需要遍历所有可能的顶点排列来找到最短路径。然而,实际应用中通过剪枝可以显著减少搜索空间,但剪枝效果的好坏很大程度上取决于问题的具体情况和剪枝策略的设计。适用于顶点数量较少时,或当存在非常有效的剪枝条件可以显著减少搜索空间时。 - 状态压缩 DP 方法的时间复杂度:状态压缩DP方法解决这个问题的时间复杂度是 。这里
n是顶点数量,2^n代表所有可能的顶点状态(每个顶点可以在路径中或不在路径中,因此是2的n次方种状态),而对于每个状态,你需要考虑n个可能的最后一个顶点,以及从另一个顶点转移到这个顶点的情况(大约是n的复杂度)。相比于递归+剪枝方法,状态压缩DP的时间复杂度在理论上更高效,特别是在顶点数量较多时。适用于顶点数量中等规模(如 20 左右)的情况。
树形 DP
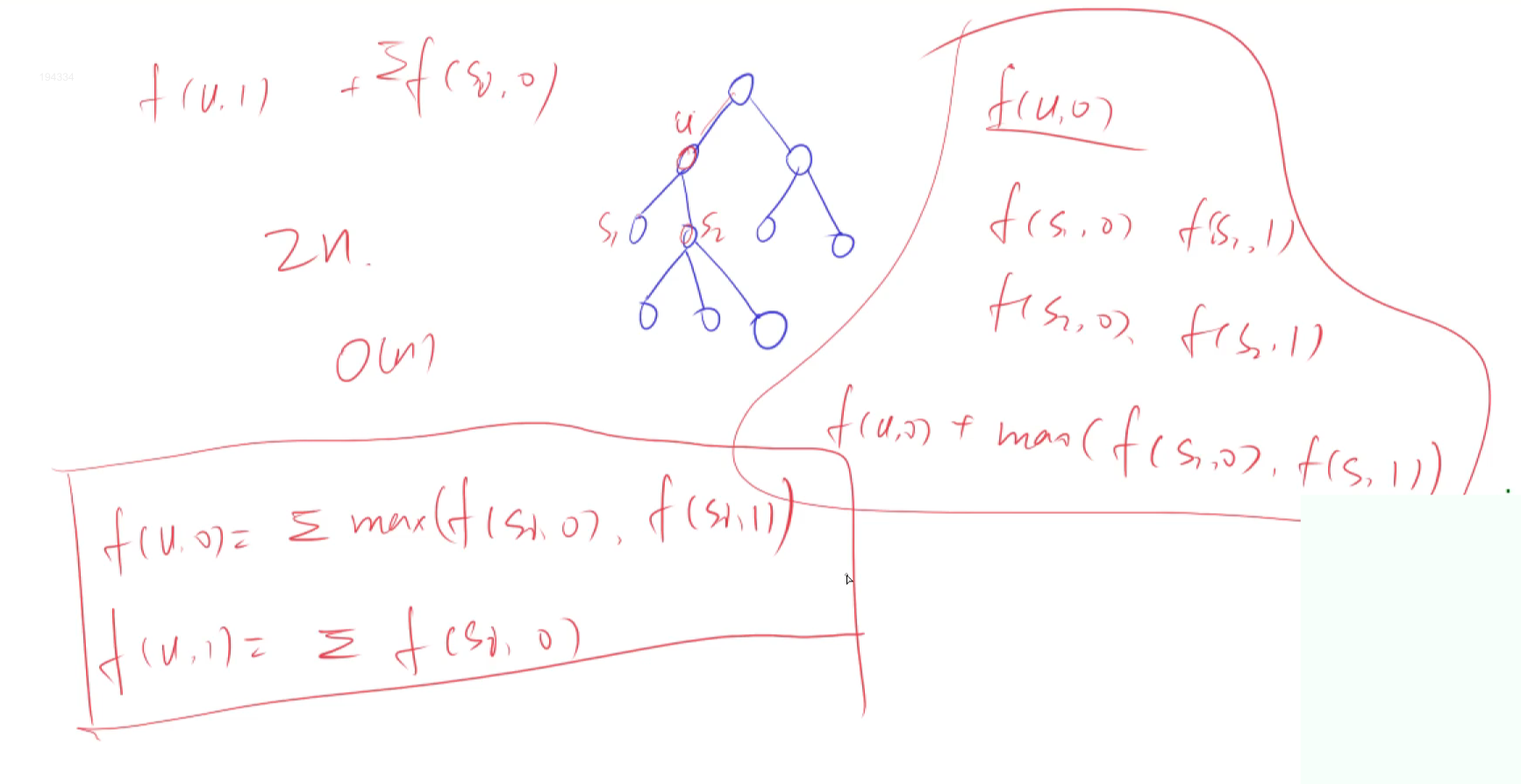
285. 没有上司的舞会

// 没有上司的舞会
#include <iostream>
using namespace std;
const int N = 6010;
int n; // 职员数量
int f[N][2]; // f[u][0]表示所有从以u为根的子树中进行选择,并且不选u这个点的方案的最大快乐指数之和;f[u][1]则为选择该点的方案;
int h[N], e[N], ne[N], idx; // 邻接表存储
int happy[N]; // 员工的快乐指数
bool has_fa[N]; // 员工是否有上司?
void add(int a, int b) { // a---->b, a是上级,b是下级
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void init() {
fill(h, h + N, -1);
fill(has_fa, has_fa + N, false);
f[1][0] = 0, f[1][1] = happy[1];
idx = 0;
}
void dfs(int u) { // 从根节点开始dfs
f[u][1] = happy[u];
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
dfs(j);
f[u][1] += f[j][0];
f[u][0] += max(f[j][0], f[j][1]);
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> happy[i];
init();
while (--n) {
int l, k; // 记录职员上下级关系,k是l的上级
cin >> l >> k;
add(k, l);
has_fa[l] = true;
}
int root = 1;
while (has_fa[root]) root++;
dfs(root);
cout << max(f[root][1], f[root][0]);
return 0;
}何时需要
st[N]标记是否访问过?为什么树的重心那题用到深搜需要用
st[N]来标记该点是否被遍历过,而这题的树形dp却不要呢?在哪些情况dfs下需要用st数组来标记,哪些又不需要呢?
if (st[j]) continue;怎么理解?标记访问过j节点,如果我当前需要知道j节点及其子节点的sum(递归返回值dfs(j))来处理最大联通子图的节点数,但我因为访问过j节点而跳过了,会不会导致当前节点的sum和res不是最终想要的结果。- 对于父节点,每个邻接点都没有被标记过,所以不会跳过。对于子节点,它的邻接点是包含父节点的(无向图),为了避免往上搜陷入无限递归,把父节点标记为访问过是必要的。
总结而言就是由于树的重心是无向图,故而父子之间都有指向,为了防止无限递归故而需要st数组,而没有上司的舞会这题是有向图,不存在父子间相互指向的问题,故而无需st数组
记忆化搜索
901. 滑雪
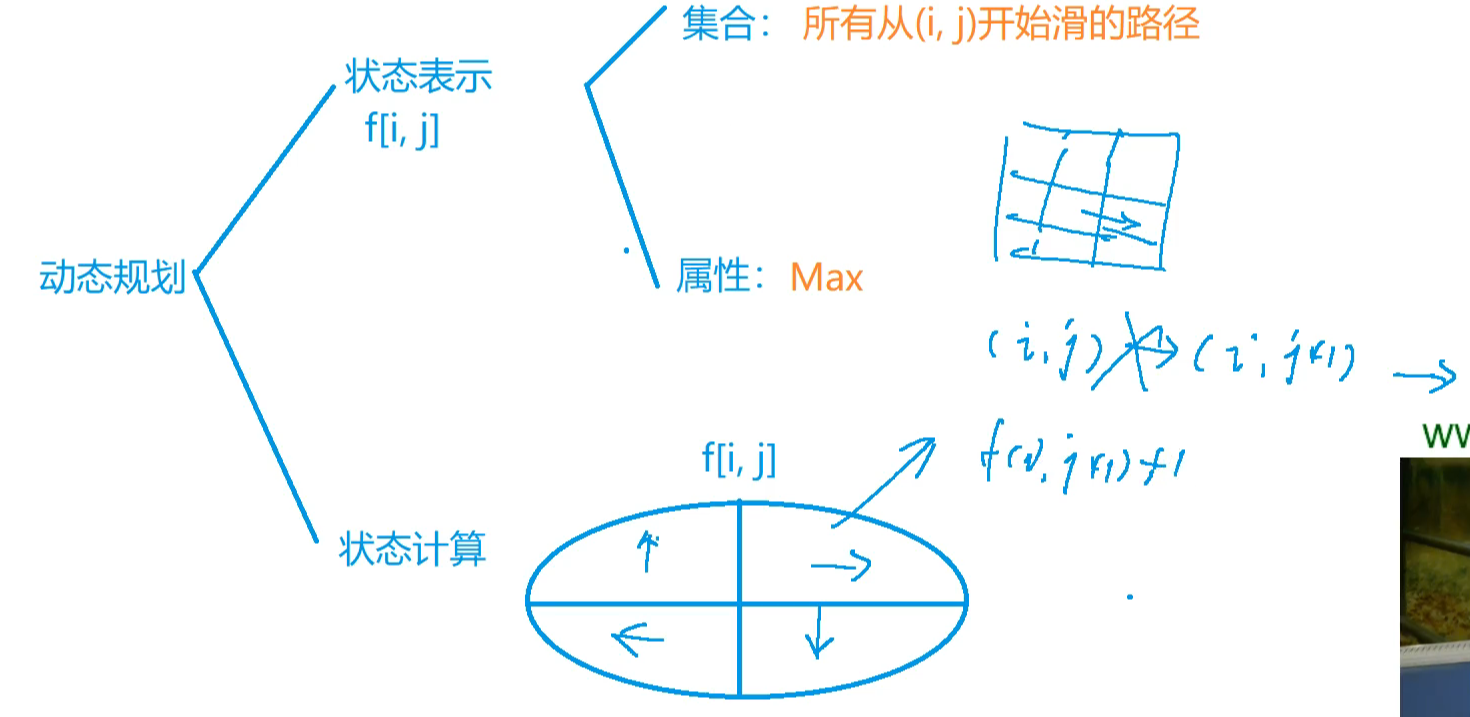
几个要求:
- 要能滑动下去
- 不能存在环(不过这个由第(1)个条件可以保障)
// 滑雪
#include <iostream>
using namespace std;
const int N = 310;
int ski_ground[N][N]; // 记录滑雪场(矩阵的数据)
int n, m; // 滑雪场的长宽,即矩阵的尺寸
int f[N][N]; // f[i][j]表示所有从(i,j)点开始划的路径的最大长度
int dx[4] = {-1, 0, 1, 0},
dy[4] = {0, 1, 0, -1}; // 左上右下四个方向移动
int slide_dist(int x, int y) { // 从坐标(x,y)可以往下滑动的最远距离
int &v = f[x][y];
if (v != -1) return v; // 如果已经滑过该点,直接返回该点可滑动的最远距离f[x][y]即可
v = 1; // 至少能在本点滑动
for (int i = 0; i < 4; i++) { // 试探性地向四个方向移动
int a = x + dx[i], b = y + dy[i]; // 从(x,y)移动后的坐标(a,b)
if (a >= 1 && a <= n && b >= 1 && b <= m && ski_ground[x][y] > ski_ground[a][b])
//(a,b)不能越界,且移动至少一步,且高度应比(x,y)要小
v = max(v, slide_dist(a, b) + 1); // 递归地查找该点的最长移动距离
}
return v;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> ski_ground[i][j];
fill(f[0], f[0] + N * N, -1);
int res = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
res = max(res, slide_dist(i, j));
cout << res << endl;
return 0;
}- 所谓记忆化搜索,就是利用
f[i][j]进行记录,当遍历到这个点的时候往下走的最大步数,也就是无论之前走了几步,都无所谓,所以不管最开始走的这条路线是不是最远的,从这个点开始能走的最远距离已经被计算出来了,所以只要下次走到这一步,就可以直接调用这个点,不用再进行多余的重复计算。