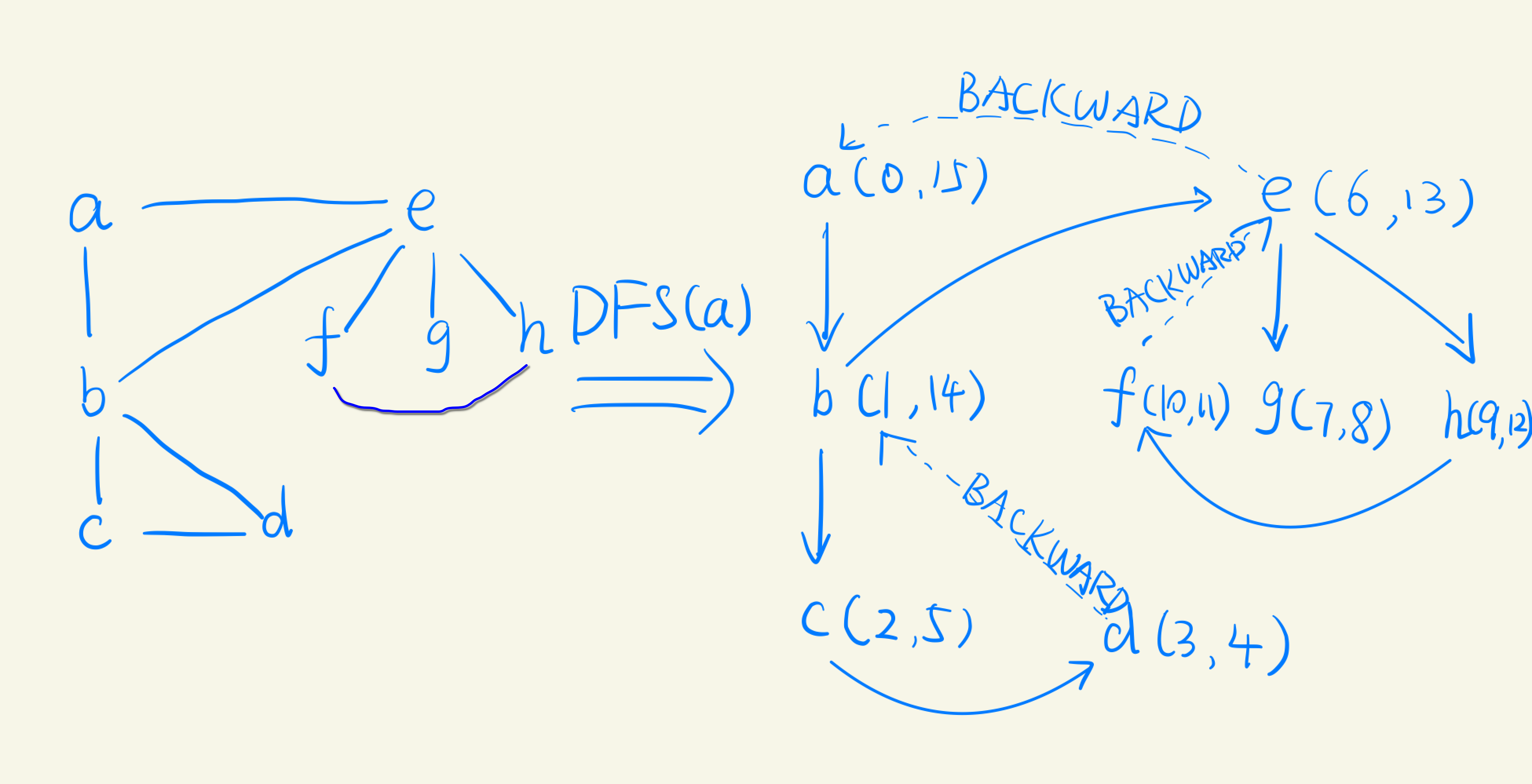80-Graph

基本术语

G=(V; E):

G: Graph
V: Vertex, nums = |V|
E: Edge, nums = |E|
同一条边的两个顶点，彼此邻接（adjacency）
同一顶点自我邻接，构成自环（self-loop）
不含自环及重边，即为简单图（simple graph），而非简单（non-simple）图，暂不讨论
顶点与其所属的边，彼此关联（incidence）
顶点的度（degree/valency）：与同一顶点关联的边数

无向图、有向图

若邻接顶点 u 和 v 的次序无所谓则 (u, v)为无向边（undirected edge）
所有边均无方向的图，即无向图（undigraph）
反之，有向图（digraph）中均为有向边（directed edge）, u、v 分别称作边 (u, v)的尾（tail）、头（head）
无向边、有向边并存的图，称作混合图（mixed graph）
有向图通用性更强，故本章主要针对有向图介绍相关结构及算法。

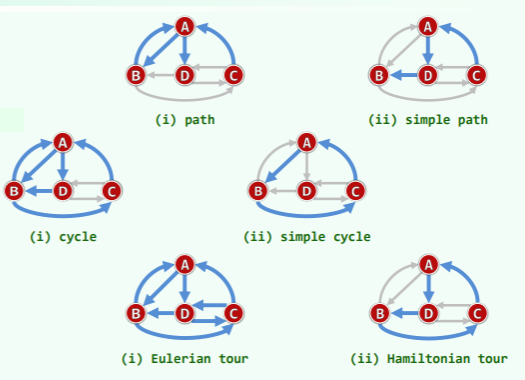
路径、环路

路径 $π$ = <v0, v1, …, vk>
长度| $π$ | = k
简单路径：vi != vj 除非 i = j
环/环路：v0 = vk
有向无环图（DAG）:
- 欧拉环路：| $π$ | = |E| 各边恰好出现一次
- 哈密尔顿环路：| $π$ | = |V| 各顶点恰好出现一次
- 欧拉环路和哈密尔顿环路都不唯一

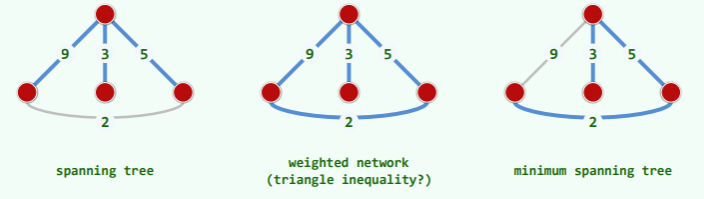
支撑树、带权网络

图 G = (V; E)的子图 T = (V; F)若是树，即为其支撑树（spanning tree）同一图的支撑树，通常并不唯一
各边 e 均有对应的权值 wt (e)，则为带权网络（weighted network）
同一网络的支撑树中，总权重最小者为最小支撑树（MST）

图的存储结构

ADT

using VStatus = enum { UNDISCOVERED, DISCOVERED, VISITED }; //顶点状态
using EType = enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD }; //边在遍历树中所属的类型
 
template <typename Tv, typename Te> //顶点类型、边类型
class Graph { //图Graph模板类
private:
	void reset() { //所有顶点、边的辅助信息复位
	    for ( Rank v = 0; v < n; v++ ) { //所有顶点的
	        status( v ) = UNDISCOVERED; dTime( v ) = fTime( v ) = -1; //状态，时间标签
	        parent( v ) = -1; priority( v ) = INT_MAX; //（在遍历树中的）父节点，优先级数
	        for ( Rank u = 0; u < n; u++ ) //所有边的
	            if ( exists( v, u ) ) type( v, u ) = UNDETERMINED; //类型
	    }
	}
	void BFS( Rank, Rank& ); //（连通域）广度优先搜索算法
	void DFS( Rank, Rank& ); //（连通域）深度优先搜索算法
	void BCC( Rank, Rank&, Stack<Rank>& ); //（连通域）基于DFS的双连通分量分解算法
	bool TSort( Rank, Rank&, Stack<Tv>* ); //（连通域）基于DFS的拓扑排序算法
	template <typename PU> void PFS( Rank, PU ); //（连通域）优先级搜索框架
public:
// 顶点
   Rank n; //顶点总数
   virtual Rank insert( Tv const& ) = 0; //插入顶点，返回编号
   virtual Tv remove( Rank ) = 0; //删除顶点及其关联边，返回该顶点信息
   virtual Tv& vertex( Rank ) = 0; //顶点的数据（该顶点的确存在）
   virtual Rank inDegree( Rank ) = 0; //顶点的入度（该顶点的确存在）
   virtual Rank outDegree( Rank ) = 0; //顶点的出度（该顶点的确存在）
   virtual Rank firstNbr( Rank ) = 0; //顶点的首个邻接顶点
   virtual Rank nextNbr( Rank, Rank ) = 0; //顶点（相对当前邻居的）下一邻居
   virtual VStatus& status( Rank ) = 0; //顶点的状态
   virtual Rank& dTime( Rank ) = 0; //顶点的时间标签dTime
   virtual Rank& fTime( Rank ) = 0; //顶点的时间标签fTime
   virtual Rank& parent( Rank ) = 0; //顶点在遍历树中的父亲
   virtual int& priority( Rank ) = 0; //顶点在遍历树中的优先级数
// 边：这里约定，无向边均统一转化为方向互逆的一对有向边，从而将无向图视作有向图的特例
   Rank e; //边总数
   virtual bool exists( Rank, Rank ) = 0; //边(v, u)是否存在
   virtual void insert( Te const&, int, Rank, Rank ) = 0; //在两个顶点之间插入指定权重的边
   virtual Te remove( Rank, Rank ) = 0; //删除一对顶点之间的边，返回该边信息
   virtual EType& type( Rank, Rank ) = 0; //边的类型
   virtual Te& edge( Rank, Rank ) = 0; //边的数据（该边的确存在）
   virtual int& weight( Rank, Rank ) = 0; //边(v, u)的权重
// 算法
   void bfs( Rank ); //广度优先搜索算法
   void dfs( Rank ); //深度优先搜索算法
   void bcc( Rank ); //基于DFS的双连通分量分解算法
   Stack<Tv>* tSort( Rank ); //基于DFS的拓扑排序算法
   void prim( Rank ); //最小支撑树Prim算法
   void dijkstra( Rank ); //最短路径Dijkstra算法
   template <typename PU> void pfs( Rank, PU ); //优先级搜索框架
};

邻接矩阵与关联矩阵

Adjacency matrix: 记录顶点之间的邻接关系

矩阵元素与图中可能存在的边，一一对应
- A (v, u)=1 当且仅当顶点 v 与 u 之间存在一条边
- A (v, u)=0 当且仅当顶点 v 与 u 之间不存在边
只考察简单图，则对角线统一设置为 0
空间复杂度为 Θ(n^2)，与图中实际拥有的边数无关，空间利用率=2e/(n^2)

Incidence matrix: 记录顶点与边之间的连接关系

空间复杂度为 Θ(n * e)=O (n^3)
空间利用率=2e/ne=2/n

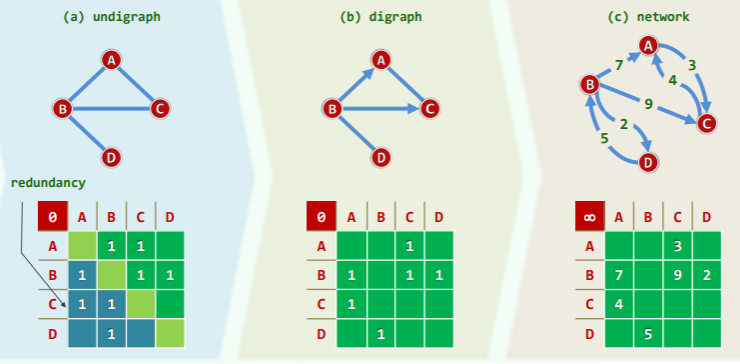
可以看到无向图的邻接矩阵中，有一半是冗余的。

邻接矩阵的模板实现

#include "Vector/Vector.h" //引入向量
#include "Graph/Graph.h" //引入图ADT

template <typename Tv> struct Vertex { //顶点对象（为简化起见，并未严格封装）
	Tv data; int inDegree, outDegree; VStatus status; //数据、出入度数、状态
	Rank dTime, fTime; //时间标签
	Rank parent; int priority; //在遍历树中的父节点、优先级数
	Vertex( Tv const& d = (Tv)0 ) : //构造新顶点
	    data( d ), inDegree( 0 ), outDegree( 0 ), status( UNDISCOVERED ), dTime( -1 ),
	    fTime( -1 ), parent( -1 ), priority( INT_MAX ) {} //暂不考虑权重溢出
};

template <typename Te> struct Edge { //边对象（为简化起见，并未严格封装）
	Te data; int weight;
	EType type; //数据、权重、类型
	Edge( Te const& d, int w ) : data( d ), weight( w ), type( UNDETERMINED ) {} //构造
};

template <typename Tv, typename Te> //顶点类型、边类型
class GraphMatrix : public Graph<Tv, Te> { //基于向量，以邻接矩阵形式实现的图
private:
	Vector<Vertex<Tv>> V; //顶点集（向量）
	Vector<Vector<Edge<Te>*>> E; //边集（邻接矩阵）
public:
	GraphMatrix() { n = e = 0; } //构造
	~GraphMatrix() { //析构
	    for ( Rank v = 0; v < n; v++ ) //所有动态创建的
	        for ( Rank u = 0; u < n; u++ ) //边记录
		        delete E[v][u]; //逐条清除
	}
	...
}; //Graph

邻接矩阵的静态操作

template <typename Tv, typename Te>
class GraphMatrix : public Graph<Tv, Te> {
private:
	...
public:
	...
/**********************
 * 顶点的基本操作：查询第v个顶点（0 <= v < n）
***********************/
	virtual Tv& vertex( Rank v ) { return V[v].data; } //数据
	virtual Rank inDegree( Rank v ) { return V[v].inDegree; } //入度
	virtual Rank outDegree( Rank v ) { return V[v].outDegree; } //出度
	virtual Rank firstNbr( Rank v ) { return nextNbr( v, n ); } //首个邻接顶点
	virtual Rank nextNbr( Rank v, Rank u ) //相对于顶点u的下一邻接顶点（改用邻接表效率更高）
	    { while ( ( -1 != --u ) && !exists( v, u ) ); return u; } //逆向线性试探
	virtual VStatus& status( Rank v ) { return V[v].status; } //状态
	virtual Rank& dTime( Rank v ) { return V[v].dTime; } //时间标签dTime
	virtual Rank& fTime( Rank v ) { return V[v].fTime; } //时间标签fTime
	virtual Rank& parent( Rank v ) { return V[v].parent; } //在遍历树中的父亲
	virtual int& priority( Rank v ) { return V[v].priority; } //在遍历树中的优先级数


/**********************
 * 边的基本操作：查询顶点v与u之间的联边（0 <= v, u < n且exists(v, u)）
***********************/
	virtual bool exists( Rank v, Rank u ) //边(v, u)是否存在
	    { return ( v < n ) && ( u < n ) && ( E[v][u] != NULL ); }
	virtual EType& type( Rank v, Rank u ) { return E[v][u]->type; } //边(v, u)的类型
	virtual Te& edge( Rank v, Rank u ) { return E[v][u]->data; } //边(v, u)的数据
	virtual int& weight( Rank v, Rank u ) { return E[v][u]->weight; } //边(v, u)的权重

};

邻接矩阵的动态操作

/**********************
 * 顶点的动态操作
***********************/
	virtual Rank insert( Tv const& vertex ) { //插入顶点，返回编号
	    for ( Rank u = 0; u < n; u++ ) E[u].insert( NULL ); n++; //各顶点预留一条潜在的关联边
	    E.insert( Vector<Edge<Te>*>( n, n, (Edge<Te>*)NULL ) ); //创建新顶点对应的边向量
	    return V.insert( Vertex<Tv>( vertex ) ); //顶点向量增加一个顶点
	}
	virtual Tv remove( Rank v ) { //删除第v个顶点及其关联边（0 <= v < n）
	    for ( Rank u = 0; u < n; u++ ) //所有
	        if ( exists( v, u ) ) //出边
	        { delete E[v][u]; V[u].inDegree--; e--; } //逐条删除
	    E.remove( v ); n--; //删除第v行
	    Tv vBak = vertex( v ); V.remove( v ); //删除顶点v
	    for ( Rank u = 0; u < n; u++ ) //所有
	        if ( Edge<Te>* x = E[u].remove( v ) ) //入边
            { delete x; V[u].outDegree--; e--; } //逐条删除
	    return vBak; //返回被删除顶点的信息
	}

/**********************
 * 边的动态操作
***********************/
	virtual void insert( Te const& edge, int w, Rank v, Rank u ) { //插入权重为w的边(v, u)
	    if ( exists( v, u ) ) return; //确保该边尚不存在
	    E[v][u] = new Edge<Te>( edge, w ); //创建新边
	    e++; V[v].outDegree++; V[u].inDegree++; //更新边计数与关联顶点的度数
	}
	virtual Te remove( Rank v, Rank u ) { //删除顶点v和u之间的联边（exists(v, u)）
	    Te eBak = edge( v, u ); delete E[v][u];
	    E[v][u] = NULL; //备份后删除边记录
	    e--; V[v].outDegree--; V[u].inDegree--; //更新边计数与关联顶点的度数
	    return eBak; //返回被删除边的信息
	}

邻接矩阵的性能分析

直观，易于理解和实现
适用范围广泛，尤其适用于稠密图（dense graph）
判断两点之间是否存在联边：O (1)
获取顶点的（出/入）度数：O (1)（任何动态操作都会更新一遍顶点的度）
添加、删除边后更新度数：O (1)
扩展性（scalability）：得益于 Vector 良好的控制策略，空间溢出等情况可被“透明地”处理

缺点：

Θ(n^2)空间，与边数无关！
不妨考察一类特定的图——平面图（planar graph）：可嵌入于平面的图
Euler’s formula (1750)： v - e + f - c = 1, for any PG
平面图：e ⇐ 3 * n - 6 = O (n) << n^2 此时，空间利用率 ≈ 1/n
稀疏图（sparse graph）空间利用率同样很低，可采用压缩存储技术 (只存非零元素的坐标和权值)

邻接表

思路：为避免邻接矩阵的空间浪费，则将邻接矩阵的各行组织成为列表，只记录存在的边及其权值。

等效于每一顶点 v 对应于列表 $L_{v} = {u ∣ < v, u >\in E}$ :

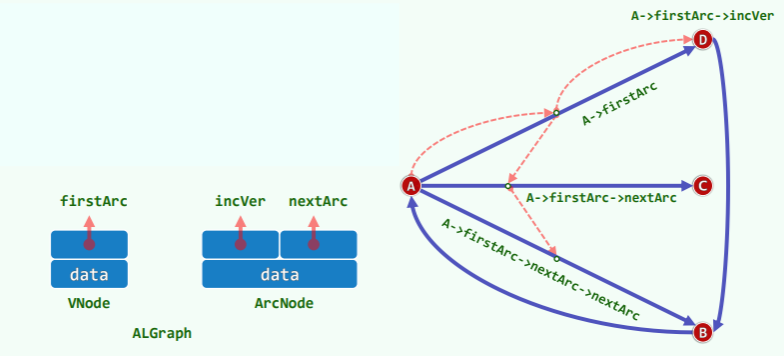
实例如下：

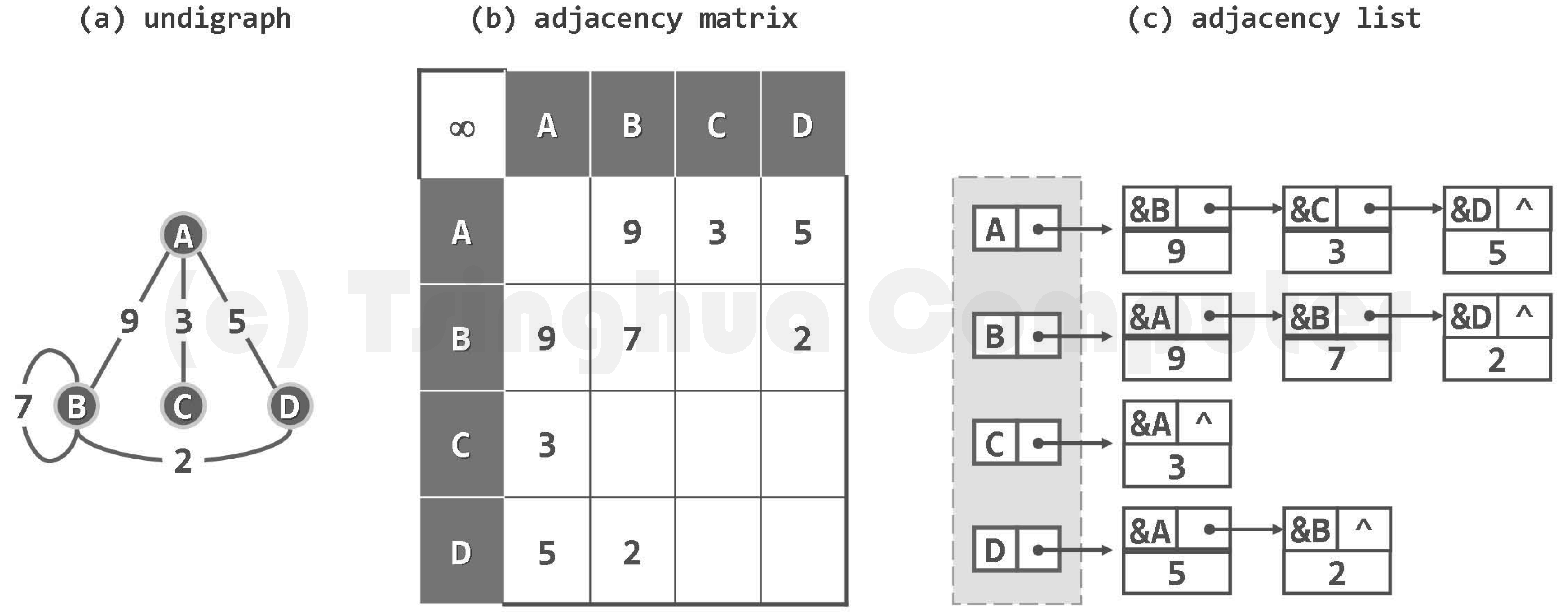
4 顶点 5 条弧：邻接矩阵需要 16 个单元的二维矩阵，邻接表则需要 9 个单元和 4 个表头；
在稀疏图中的优势更明显。

空间复杂度

有向图：O (n+e)
无向图：O (n+2e)
- 无向弧被重复存储，若要改进，只需要…（邻接多重表）
平面图：O (n+3n)

时间复杂度

建立邻接表：O (n+e) //递增式构造，如何实现？
枚举所有以顶点 v 为尾的弧：O (1+deg (v)) //遍历 v 的邻接表
枚举（无向图中）顶点 v 的邻居：O (1+deg (v)) //遍历 v 的邻接表
枚举所有以顶点 v 为头的弧：O (n+e) //遍历所有邻接表
- 可改进至 O (1+deg (v)) //办法是建立逆邻接表，空间复杂度需要增加…
计算顶点 v 的出度/入度：
- 增加度数的记录域：O (n)的附加空间
- 增加/删除弧时更新度数：O (1)时间，总体 O (e)时间
- 每次查询需要：O (1) 时间

给定顶点 u 和 v，判断<u, v>是否属于 E：

有向图：搜索 u 的邻接表，时间复杂度为 O (deg (u)) = O (e)
无向图：搜索 u 或 v 的邻接表，O (max (deg (u), deg (v)))=O (e)
并行搜索：O (2 * min (deg (u), deg (v)))=O (e)
如何达到邻接矩阵的 O (1)?
- 利用散列技术，使弧的判定达到 expected-O (1) //与邻接矩阵相同
- 空间：O (n+e) //与邻接表相同

邻接矩阵与邻接表的取舍原则

邻接矩阵适用的场合：
- 经常检测边的存在
- 经常做边的插入和删除操作
- 图的规模固定
- 稠密图
邻接表适用的场合：
- 经常计算顶点的度数
- 顶点数目不确定
- 经常做遍历
- 稀疏图

十字链表

十字链表 (orthogonal-list) 存储的对象是有向图。同邻接表相同的是，图中每个顶点各自构成一个链表，为链表的首元结点。
同时，对于有向图中的弧来说，有弧头和弧尾。一个顶点所有的弧头的数量即为该顶点的入度，弧尾的数量即为该顶点的出度。
每个顶点构成的链表中，以该顶点作为弧头的弧单独构成一个链表，以该顶点作为弧尾的弧也单独构成一个链表，两个链表的表头都为该顶点构成的头结点。
这样，由每个顶点构建的链表按照一定的顺序存储在数组中，就构成了十字链表。

节点结构

所以，十字链表中由两种结点构成：顶点结点和弧结点。各自的结构构成如下图所示：

弧结点中， tailvex 和 headvex 分别存储的是弧尾和弧头对应的顶点在数组中的位置下标； hlink 和 tlink 为指针域，分别指向弧头相同的下一个弧和弧尾相同的下一个弧； info 为指针域，存储的是该弧具有的相关信息，例如权值等。
顶点结点中，data 域存储该顶点含有的数据； firstin 和 firstout 为两个指针域，分别指向以该顶点为弧头和弧尾的首个弧结点。

实例

例如，使用十字链表存储有向图 5（A），构建的十字链表如图（B）所示,构建代码实现为：

#define  MAX_VERTEX_NUM 20
#define  InfoType int//图中弧包含信息的数据类型
#define  VertexType int
typedef struct ArcBox{
    int tailvex,headvex;//弧尾、弧头对应顶点在数组中的位置下标
    struct ArcBox *hlik,*tlink;//分别指向弧头相同和弧尾相同的下一个弧
    InfoType *info;//存储弧相关信息的指针
}ArcBox;
typedef struct VexNode{
    VertexType data;//顶点的数据域
    ArcBox *firstin,*firstout;//指向以该顶点为弧头和弧尾的链表首个结点
}VexNode;
typedef struct {
    VexNode xlist[MAX_VERTEX_NUM];//存储顶点的一维数组
    int vexnum,arcnum;//记录图的顶点数和弧数
}OLGraph;
int LocateVex(OLGraph * G,VertexType v){
    int i=0;
    //遍历一维数组，找到变量v
    for (; i<G->vexnum; i++) {
        if (G->xlist[i].data==v) {
            break;
        }
    }
    //如果找不到，输出提示语句，返回 -1
    if (i>G->vexnum) {
        printf("no such vertex.\n");
        return -1;
    }
    return i;
}
//构建十字链表函数
void CreateDG(OLGraph *G){
    //输入有向图的顶点数和弧数
    scanf("%d,%d",&(G->vexnum),&(G->arcnum));
    //使用一维数组存储顶点数据，初始化指针域为NULL
    for (int i=0; i<G->vexnum; i++) {
        scanf("%d",&(G->xlist[i].data));
        G->xlist[i].firstin=NULL;
        G->xlist[i].firstout=NULL;
    }
    //构建十字链表
    for (int k=0;k<G->arcnum; k++) {
        int v1,v2;
        scanf("%d,%d",&v1,&v2);
        //确定v1、v2在数组中的位置下标
        int i=LocateVex(G, v1);
        int j=LocateVex(G, v2);
        //建立弧的结点
        ArcBox * p=(ArcBox*)malloc(sizeof(ArcBox));
        p->tailvex=i;
        p->headvex=j;
        //采用头插法插入新的p结点
        p->hlik=G->xlist[j].firstin;
        p->tlink=G->xlist[i].firstout;
        G->xlist[j].firstin=G->xlist[i].firstout=p;
    }
}

对于链表中的各个结点来说，由于表示的都是该顶点的出度或者入度，所以结点之间没有先后次序之分，程序中构建链表对于每个新初始化的结点采用头插法进行插入。

十字链表计算顶点的度

采用十字链表表示的有向图，在计算某顶点的出度时，为 firstout 域链表中结点的个数；入度为 firstin 域链表中结点的个数。

邻接多重表

83-Adjacency-multilist
描述

前面讲过，无向图的存储可以使用邻接表，但在实际使用时，如果想对图中某顶点进行实操（修改或删除），由于邻接表中存储该顶点的节点有两个，因此需要操作两个节点。

为了提高在无向图中操作顶点的效率，本节学习一种新的适用于存储无向图的方法——邻接多重表。

注意，邻接多重表仅适用于存储无向图或无向网。

邻接多重表存储无向图的方式，可看作是邻接表和十字链表的结合。同邻接表和十字链表存储图的方法相同，都是独自为图中各顶点建立一张链表，存储各顶点的节点作为各链表的首元节点，同时为了便于管理将各个首元节点存储到一个数组中。

节点结构

各首元节点结构如图所示：

上图中各区域及其功能为：

data：存储此顶点的数据；

firstedge：指针域，用于指向同该顶点有直接关联的存储其他顶点的节点。

从上图可以看到，邻接多重表采用与邻接表相同的首元节点结构。但各链表中其他节点的结构与十字链表中相同，如下图所示：

上图节点中各区域及功能如下：

mark：标志域，用于标记此节点是否被操作过，例如在对图中顶点做遍历操作时，为了防止多次操作同一节点，mark 域为 0 表示还未被遍历；mark 为 1 表示该节点已被遍历；

ivex 和 jvex：数据域，分别存储图中各边两端的顶点所在数组中的位置下标；

ilink：指针域，指向下一个存储与 ivex 有直接关联顶点的节点；

jlink：指针域，指向下一个存储与 jvex 有直接关联顶点的节点；

info：指针域，用于存储与该顶点有关的其他信息，比如无向网中各边的权；

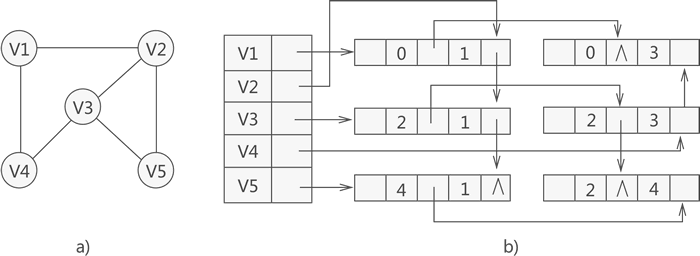
实例

综合以上信息，如果我们想使用邻接多重表存储图 a 中的无向图，则与之对应的邻接多重表如图 b 所示：

从上图中，可直接找到与各顶点有直接关联的其他顶点。比如说，与顶点 V1 有关联的顶点为存储在数组下标 1 处的 V2 和数组下标 3 处的 V4，而与顶点 V2 有关联的顶点有 3 个，分别是 V1、V3 和 V5。

实现

实例中的邻接多重表的整体结构转化为 C 语言代码如下所示：
#define MAX_VERTEX_NUM 20       //图中顶点的最大个数
#define InfoType int            //边含有的信息域的数据类型
#define VertexType int          //图顶点的数据类型
typedef enum {unvisited,visited}VisitIf;    //边标志域
typedef struct EBox{
    VisitIf mark;                 //标志域
    int ivex,jvex;          //边两边顶点在数组中的位置下标
    struct EBox * ilink,*jlink;   //分别指向与ivex、jvex相关的下一个边
    InfoType *info;           //边包含的其它的信息域的指针
}EBox;
typedef struct VexBox{
    VertexType data;          //顶点数据域
    EBox * firstedge;         //顶点相关的第一条边的指针域
}VexBox;
typedef struct {
    VexBox adjmulist[MAX_VERTEX_NUM];//存储图中顶点的数组
    int vexnum,degenum;//记录途中顶点个数和边个数的变量
}AMLGraph;
指向原始笔记的链接

图的遍历

广度优先搜索

思路

对顶点 s 进行广度优先搜索：

访问顶点s
依次访问 s 所有尚未访问的邻接顶点
依次访问它们尚未访问的邻接顶点
如此反复，直到没有尚未访问的邻接顶点

以上策略完全及过程完全等同于树的层次遍历，实际上 BFS 会构造出原图的一棵支撑树——称为 BFS-Tree：

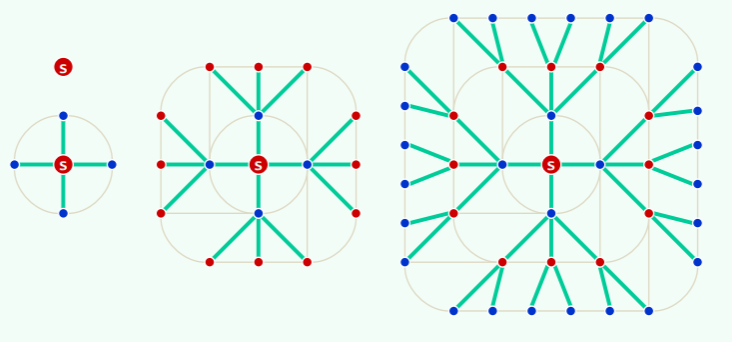
实现

//广度优先搜索BFS算法（单个连通域）
template <typename Tv, typename Te> 
void Graph<Tv, Te>::BFS( Rank v, Rank& dClock ) { // v < n
	Queue<Rank> Q;
	status( v ) = DISCOVERED; 
	Q.enqueue( v ); 
	dTime( v ) = dClock++; //起点入队
	
	for ( Rank fClock = 0; !Q.empty(); ) { //在Q变空之前，反复地
	    if ( dTime( v ) < dTime( Q.front() ) ) //dTime的增加，意味着开启新的一代，因此
	        dClock++, fClock = 0; //dTime递增，fTime复位
	    v = Q.dequeue(); //取出首顶点v，并
	    for ( Rank u = firstNbr( v ); -1 != u; u = nextNbr( v, u ) ) //考查v的每一个邻居u，视u的状态分别处理
	        if ( UNDISCOVERED == status( u ) ) { //若u尚未被发现，则发现之
		        status( u ) = DISCOVERED;//对该顶点作发现操作
		        Q.enqueue( u ); 
		        dTime( u ) = dClock;
		        
	            type( v, u ) = TREE;//引入树边，拓展BFS树
	            parent( u ) = v; 
	    } else //若u已被发现，或者甚至已访问完毕，则
	        type( v, u ) = CROSS; //将(v, u)归类于跨边
	    
	    status( v ) = VISITED; 
	    fTime( v ) = fClock++; //至此，v访问完毕
	} //for
} //BFS

实例

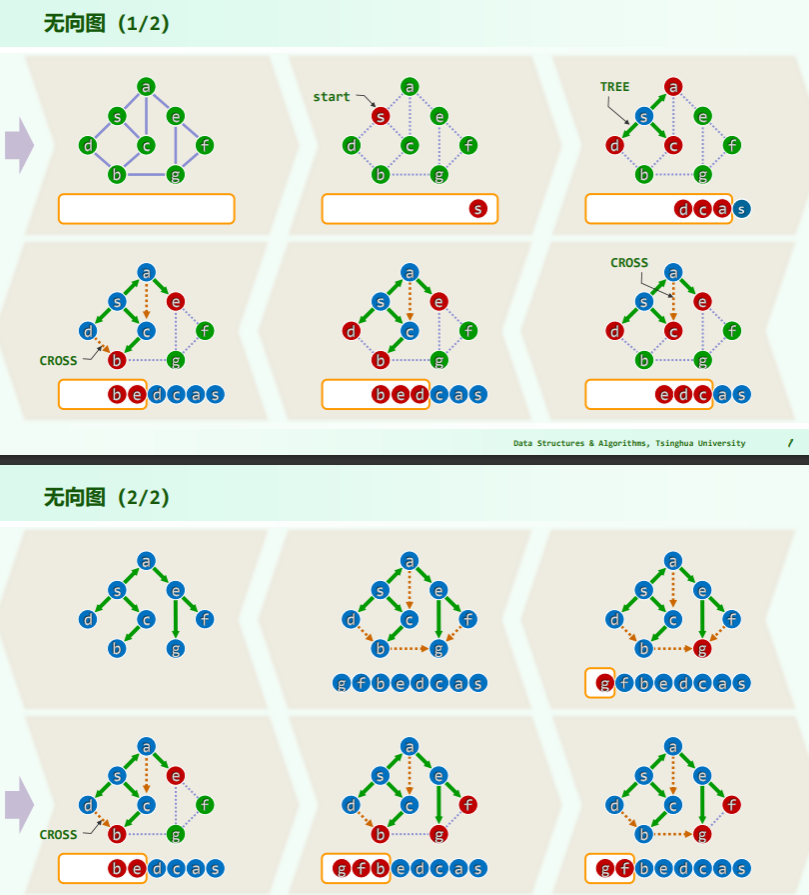
BFS 过程中顶点的状态：

UNDISCOVERED：邻居顶点未发现
DISCOVERED：邻居顶点已发现
VISITED：顶点已通过 BFS 遍历完毕
dTime：顶点进入队列的时间——代表着顶点刚被发现的时间
fTime：顶点离开队列的时间——代表顶点被访问完毕的时间

BFS 过程中边的类型：

CROSS：跨边，表示顶点的邻居 u 已经被发现或访问完毕（已出队）
TREE：树边，表示 BFS 的结果——BFS-Tree 中的一条边

推广：全图BFS

连通分量：在给定无向图中，找出其中任一顶点 s 所在的连通图； 可达分量：在给定有向图中，找出源自其中任一顶点 s 的可到达分量；

实现思路：从 s 出发作 BFS，输出所有被发现的顶点，队列空后立即中止，无需考虑其它顶点。

若图中包含多个连通/可达分量，如何对全图进行 BFS？

template <typename Tv, typename Te> //广度优先搜索BFS算法（全图）
void Graph<Tv, Te>::bfs( Rank s ) { // s < n
	reset(); Rank dClock = 0; //全图复位
	for ( Rank v = s; v < s + n; v++ ) //从s起顺次检查所有顶点
	    if ( UNDISCOVERED == status( v % n ) ) //一旦遇到尚未发现者
	        BFS( v % n, dClock ); //即从它出发启动一次BFS
} //如此可完整覆盖全图，且总体复杂度依然保持为O(n+e)

复杂度（考查无向图）：
- bfs ()初始化的 reset ()：O (n+e)
- BFS ()的迭代：
  - 外循环（while (!Q.empty)）每个顶点各进入 1 次，
  - 内循环（枚举 v 的每个邻居）：O (1+deg (v)) //邻接表
  - 故总共 $O (v \in V \sum (1 + d e g (v))) = O (n + 2 e)$
- 整个算法：O (n+e)+O (n+2e)=O (n+e)
- 有向图亦是如此！

性质与应用

边分类

经 BFS 后，所有边将确定方向且被分为两类：
- (v, u)被标记为 TREE 时，v 为 DISCOVERED 而 u 为 UNDISCOVERED
- (v, u)被标记为 CROSS 时，v 和 u 均为 DISCOVERED 或 v 为 DISCOVERED 而 u 为 VISITED

BFS-Tree/Forest

对于起始于 v 的每一连通分量/可达分量，bfs() 进入 BFS(v)恰好 1 次
进入 BFS (v)时，队列为空，v 所属分量内的每个顶点
- 迟早会已 UNDISCOVERED 状态入队一次，
- 入队后随机转化为 DISCOVERED 状态并生成一条树边，
- 且迟早会出队且将 v 转换为 VISITED 状态，
- 同样退出 BFS (v)时队列也为空
BFS (v)以 v 为根，生成一棵 BFS-Tree
bfs ()生成一个 BFS 森林，包含 c 棵树、n-c 条树边、e-n+c 条跨边

最短路径

无向图中，将顶点 v 到 u 的距离记作 dist (v, u)，在 v 的视角里，简记作 dist(u)，下面的描述就是这个意思
BFS 过程中，队列 Q 的变化如下：
- 队列中的顶点按照 dist (s)单调非递减（非递增当然也可以）排列
- 相邻顶点的 dist (s)相差不超过 1
- 首、末顶点的 dist (s)相差不超过 1 （意思是队列中始终保持在相邻的层次内遍历）
- 由树边连接的顶点，dist (s)恰好差 1 ⭐
- 由跨边连接的顶点，dist (s)至多相差 1 ⭐
BFS-Tree 中从 s 到达 v 的路径，即是二者在原图中最短的通路

Erdős number

Erdős number - Wikipedia 描述协作距离

埃尔德什·帕尔的埃数是0，与其合写论文的埃数是1，一个人至少要 k 个中间人（合写论文的关系）才能与埃尔德什·帕尔有关联，则他的埃数是 k+1。例如：埃尔德什·帕尔与 A 合写论文，A 与 B 合写论文，但埃尔德什·帕尔没有与 B 合写论文，则 A 的埃数是1，B 的埃数是2。

Chow Number

Chow-Number：一道 thu-oj 的题目：

周星驰（Stephen Chow）似乎已成为了当今校园文化的代名词了。

这不，即使是影视圈的明星们，也开始通过” 周数 “（Chow Number）来衡量自己的艺术水准和文化品味了。

所谓的 “周数” 是一个（随时间不增）的函数：

chow() : {所有人}  ├→  {0, 1, 2, ..., ∞}

具体的：

1. chow(周星驰) = 0；

2. chow(x) = 1 + min( {∞} U {chow(a) | x 与 a 一起拍过某部电影 } )，x ≠ 周星驰。

任务：不幸的是，大多数急于知道自己的 Chow Number 的人，确实很难坐下来亲自计算一下（他们太忙，另外…）。作为一名正在学习数据结构的星星的影迷，你是否觉得有责任来编写一个程序帮助他们？你编写的程序需要提供以下功能：
1. 根据给定的影片数据库，建立有效的数据结构；
2. 对给定的影星名单，计算出他 / 她们的周数，并且给出相应的信息；
3. 能够处理一定规模的影片数据库（这里提供这样的一个样例数据库）；
4. 有一定的计算速度；
5. 程序健壮。
例子

% chownumber films.dat stars.dat > stars.chow

实现提示

这里已经准备好了一个数据库，里面有 “所有” 影片的信息。

即使对这样小规模的数据，如果直接搜索，程序的速度也很难令人满意，因此这样的实现将不能得分。

幸运的是，最短路径的数据结构及算法可以帮助你：将所有影星表示为图的顶点，在任何曾经合作过的两位影星之间构造一条弧。

如果弧的权值统一为 1，那么一个影星的周数实际就是他 / 她在图中到周星驰的最短路径长。

任务要求的就是找到这样一条最短路径，并输出沿途各弧（合作影片）的信息。

速度测试

你可以将自己程序的速度与这个程序对比一下：

% chownumber films.dat allstars.dat > allstars.chow

注意，要通过重定向将输出直接记入某个文件，否则，屏幕输出本身就会占用绝大部分时间。

附加功能

如果你关心的不止是周数，是否要为每位明星都写一个程序呢？

试编写一个通用的程序。比如：

% chownumber films.dat allstars.dat 孙海鹰 > sunhaiying.chow

或者

% chownumber films.dat allstars.dat 张国荣 > gege.chow

二分图

Bipartite Graph 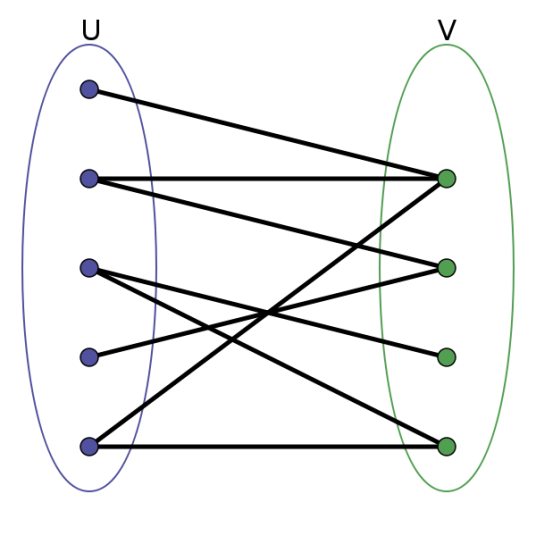二分图又称作二部图，是图论中的一种特殊模型。

设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

图的偏心率、半径、直径、中心

图/树的直径、偏心率、半径、中心

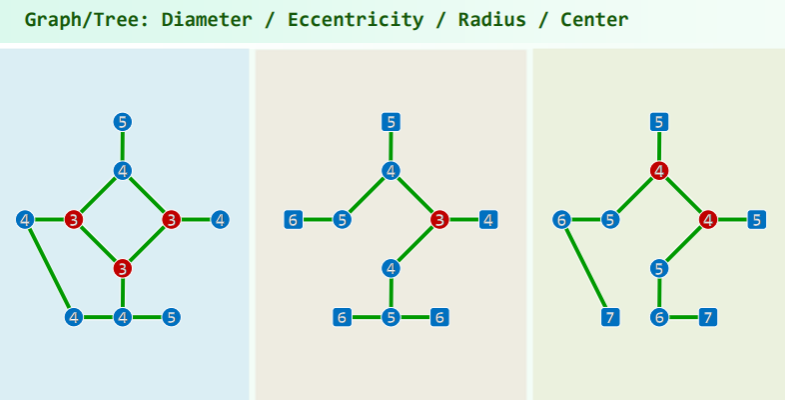
Diameter: 直径是指图中任意两个节点之间的最长路径的长度。

换句话说，它是连接图中任意两个节点的最长边的长度。

直径反映了图或树的整体大小。

Eccentricity: 对于每个节点来说，其偏心率是指从该节点到图中所有其他节点的最长路径的长度中的最大值。

偏心率衡量了一个节点到图中其他节点的距离，偏心率最小的节点被称为图的中心。

Radius: 图或树的半径是指所有节点偏心率中的最小值。

换句话说，它是图中所有节点到离它最远的节点的最短距离中的最小值。

半径反映了图或树的紧凑程度，越小表示越紧凑。

Center: 图或树的中心是指具有最小偏心率的节点集合。

这些节点是离图中其他节点最近的节点，通常是半径的节点。

中心是图或树的”核心”部分。

指向原始笔记的链接

深度优先搜索

思路

始自顶点 s 进行 DFS：

访问顶点s
- 若 s 尚有未被访问的邻居，则任取其一作为 u，递归执行 DFS (u)
- 否则，返回
若此时尚有节点未被访问，则任取一个顶点作起始点，重复上述过程直到所有顶点都被访问到

以上策略完全等效于树的先序遍历，DFS 也会构造出原树的一棵支撑树—— DFS-Tree：

实现

//深度优先搜索DFS算法（单个连通域）
template <typename Tv, typename Te> 
void Graph<Tv, Te>::DFS( Rank v, Rank& clock ) { // v < n
	dTime( v ) = clock++;
	status( v ) = DISCOVERED; //发现当前顶点v
	for ( Rank u = firstNbr( v ); - 1 != u; u = nextNbr( v, u ) ) //考查v的每一个邻居u
	    switch ( status( u ) ) { //并视其状态分别处理
	        case UNDISCOVERED : // u尚未发现，意味着支撑树可在此拓展
		        type( v, u ) = TREE; 
		        parent( u ) = v; 
		        DFS( u, clock ); break;
	        case DISCOVERED : // u已被发现但尚未访问完毕，应属被后代指向的祖先
	            type( v, u ) = BACKWARD; 
	            break;
	        default : // u已访问完毕（VISITED，有向图），则视承袭关系分为前向边或跨边
	            type( v, u ) = ( dTime( v ) < dTime( u ) ) ? FORWARD : CROSS; break;
	    }
	status( v ) = VISITED; 
	fTime( v ) = clock++; //至此，当前顶点v方告访问完毕
}

注意在设置 v 点的 dTime 时，使用的是 clock++ 语句，与 BFS 中区分 dClock 和 fClock 不同，这表明 DFS 中 dTime 和 fTime 都使用统一的时钟，并且起点 v 的 dClock——发现时间是从 0 开始计数；
如果发现邻居 u 是 UNDISCOVERED 状态，则将<v, u>设置为树边、u 的父亲设置为 v——为构造 DFSTree 作准备；并继续对 u 进行递归 DFS，clock 传递下去，因此 u 的 dTime 设置为 1；
如果发现 u 是 DISCOVERED 状态，表明 u 已被发现但尚未访问完毕（访问完毕应当是 VISITED 状态），则标记<v, u>为后向边 BACKWARD，并查找下一个邻居；若所有邻居都访问完毕，则设置为 VISITED，并设置 fTime 为 clock++；此后回退递归栈，直到栈顶元素有邻居；
如果发现 u 是 VISITED 状态，表明 u 已经访问完毕，其所有邻居（除父亲）都被访问结束，则根据 dTime 被访问时间的先后，设定<v, u>为前向边 FORWORD 抑或跨边 CROSS

实例

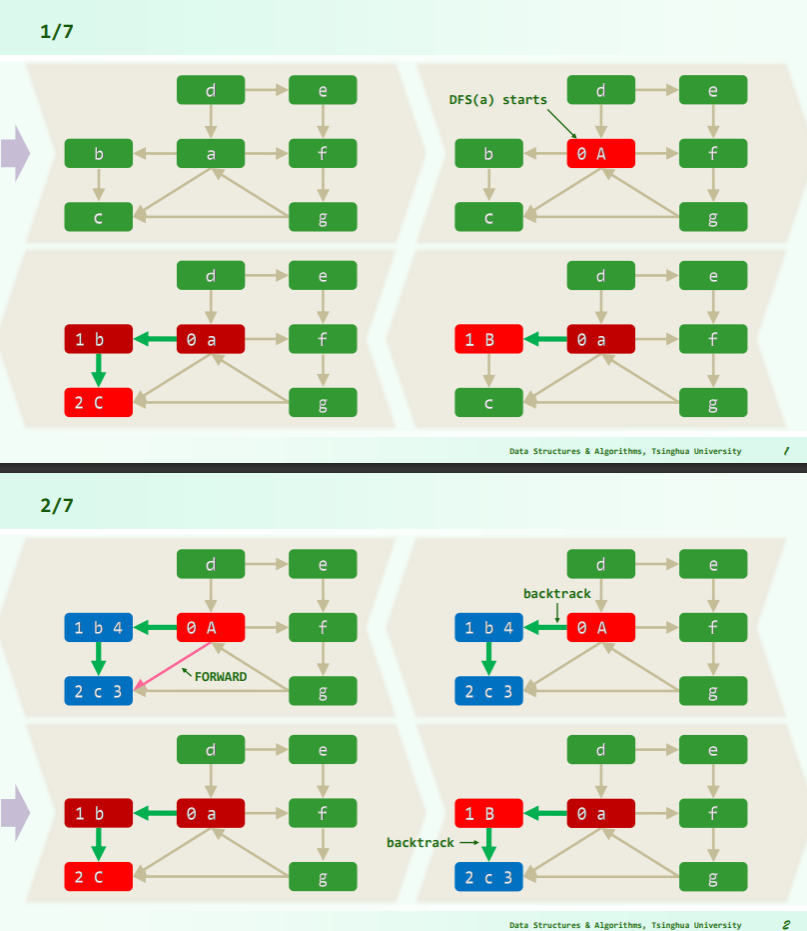
无向图

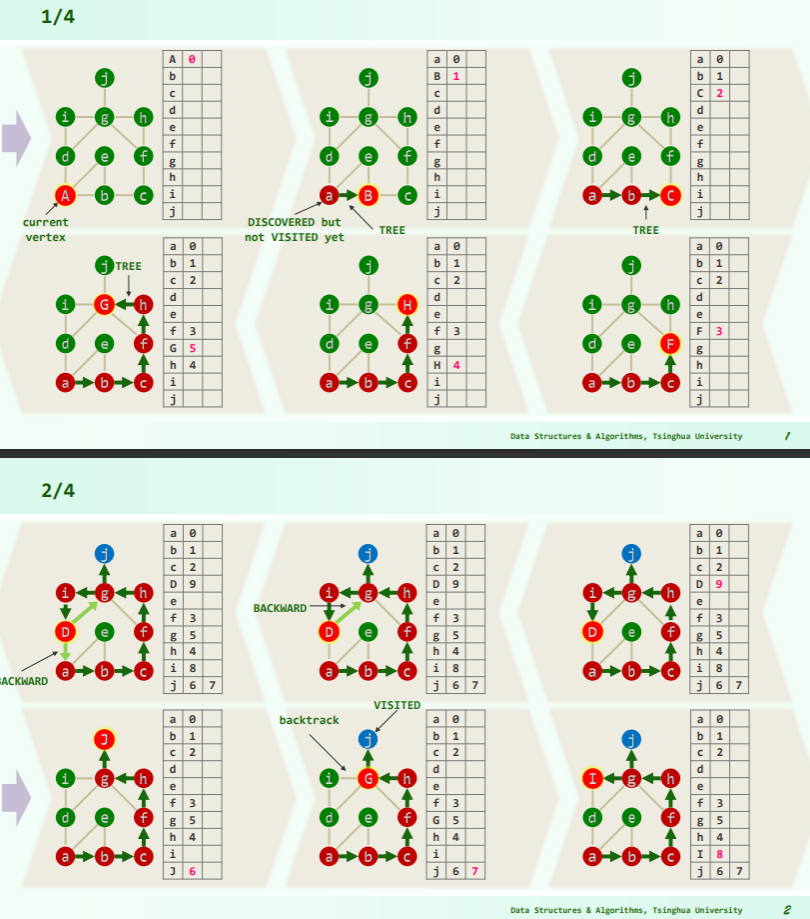
DFS 过程中顶点的状态：

UNDISCOVERED
DISCOVERED
VISITED
dTime：顶点被发现的时间
fTime：顶点被访问完毕的时间
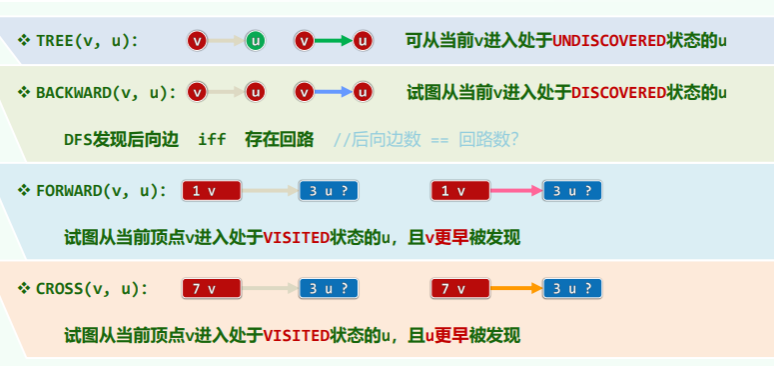
DFS 过程中边的状态：
- TREE
- CROSS：表明边的目的点 u 已经访问完毕，但是当前节点的发现时间晚于 u，这只会出现在有向图中；
- FORWARD：表明边的目的点 u 已经访问完毕，并且当前节点的发现时间还要早于 u，这只会出现在有向图中；
- BACKWARD：表明边的目的点 u 已被发现，但是还未访问完毕，从 DFSTree 的角度来看，BACKWARD 表明从树的低层向祖先的指向的边；

有向图

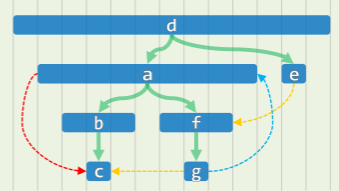
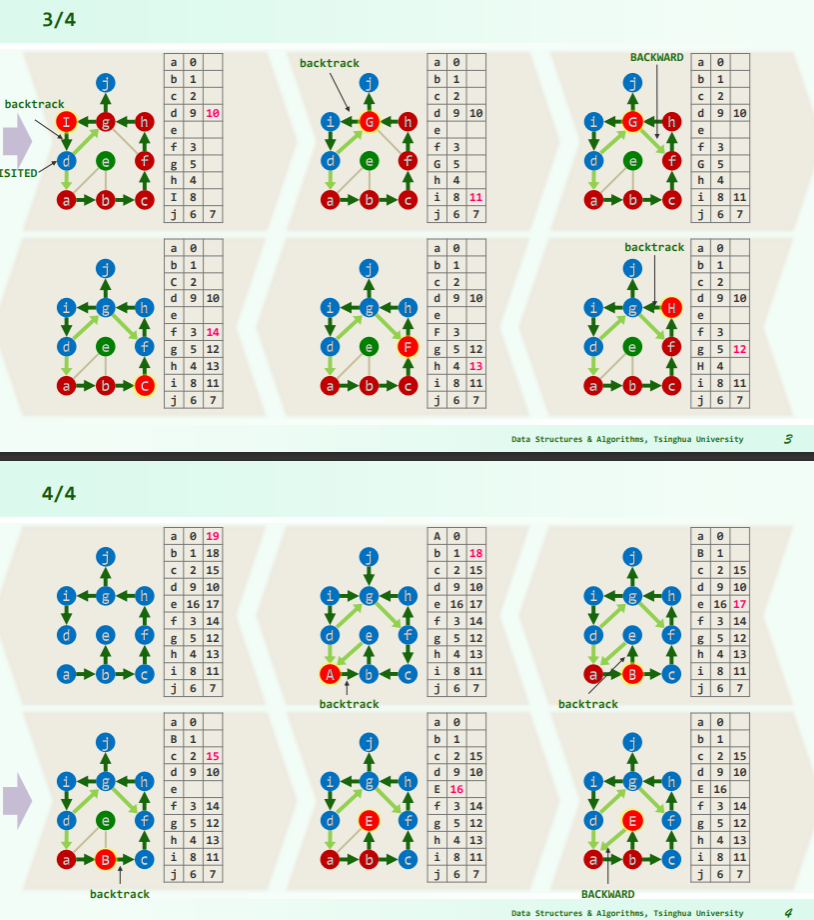
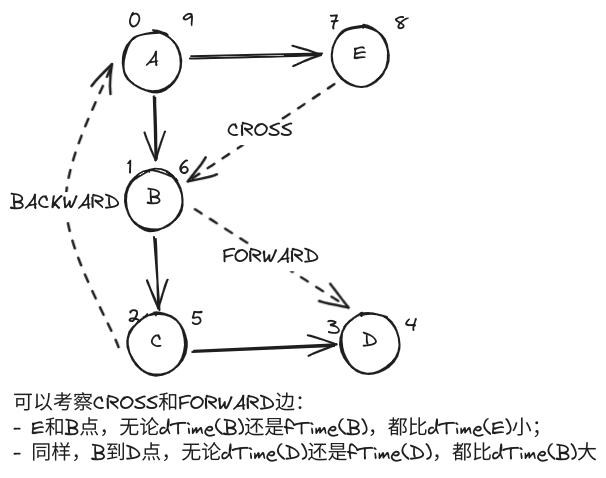
注意到 A→c 时 c 已经访问完毕，而 dTime (A)<dTime (c)，表明 a 的深度较浅，由此 <a, c> 是一条 FORWARD 前向边；

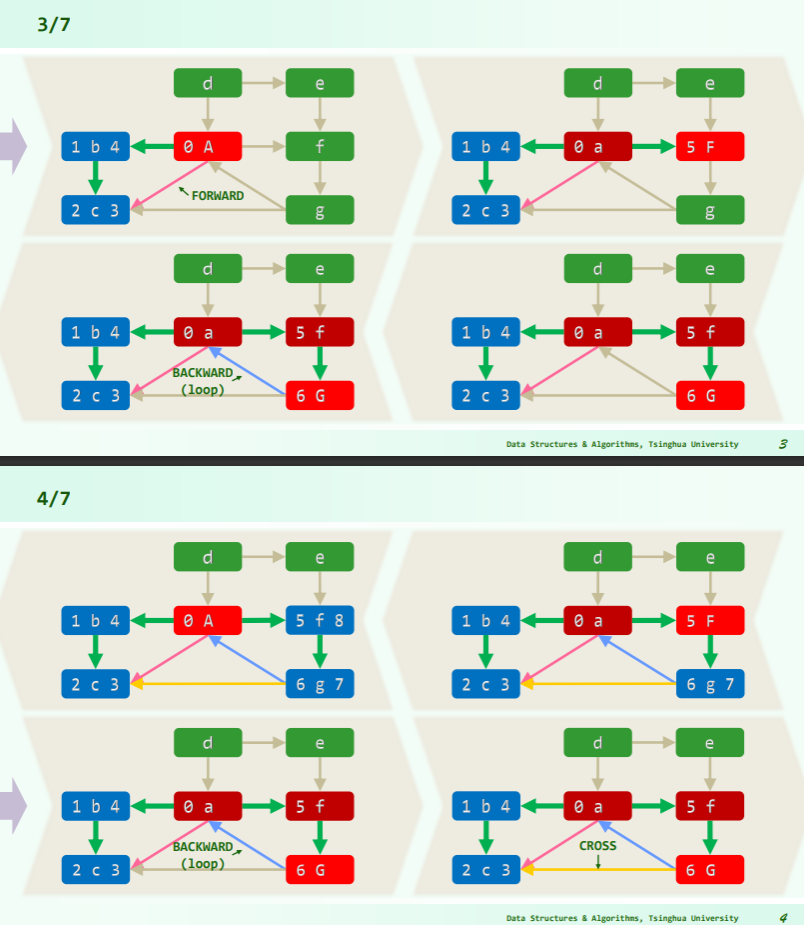
注意到此处 G→a 的 BACKWARD 出现了 loop，表明 a→f→g 构成了一条环路；
而 G→c 时，c 已访问完毕，且 dTime (G)>dTime (c)，由此 <g, c> 是一条 CROSS 跨边；

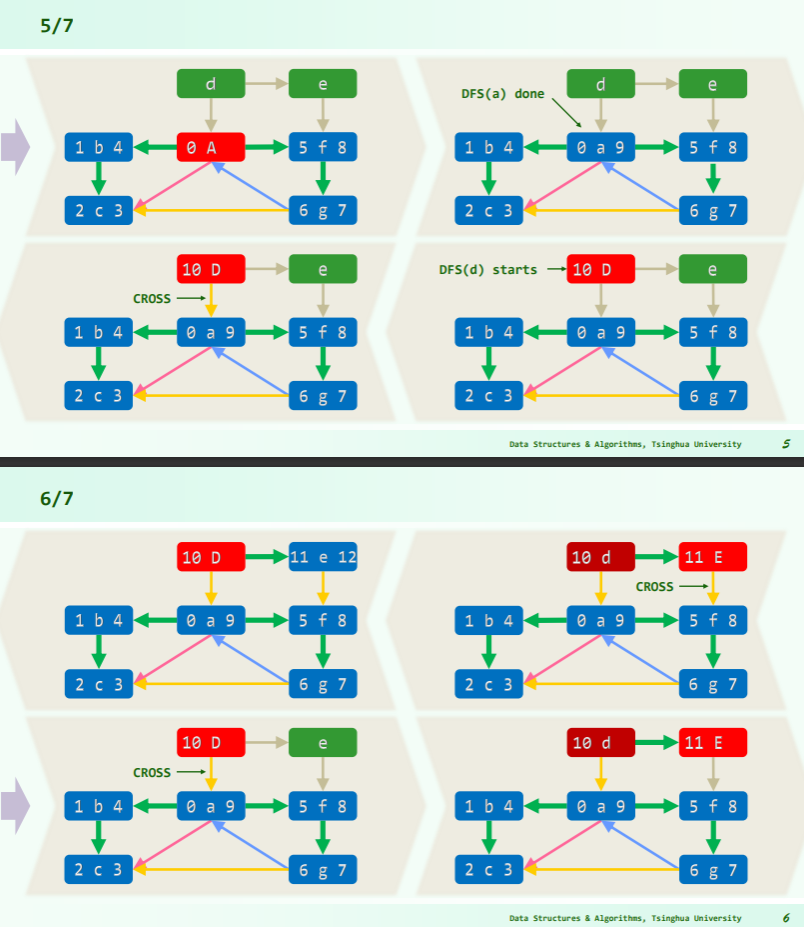
注意到此时 a 所属的连通分量已经访问完毕，但是全图仍有未访问节点，于是根据邻接表找到它们，进行 dfs 全局遍历；
对后访问的连通分量，其指向前一个访问完毕的连通分量的边都是 CROSS 跨边；

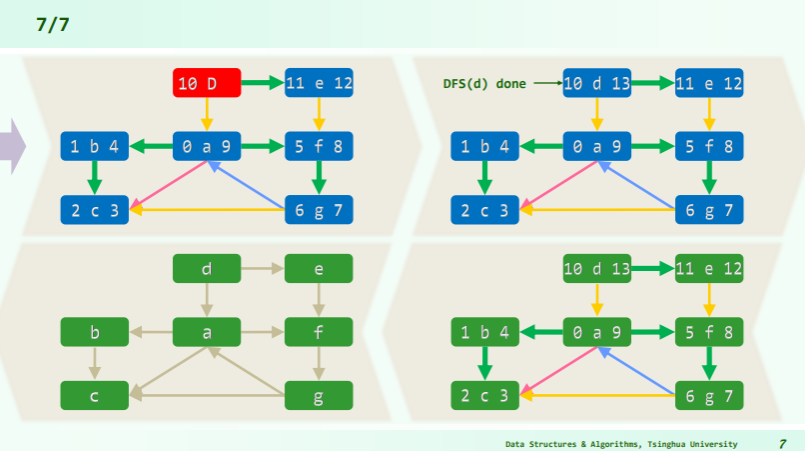
[! note] 与拓扑排序的联系注意到，在上图中从 a 开始 DFS，并不能一趟扫描完毕，但若是从 d 开始 DFS，则可以一趟扫描完毕。对于有向无环连通图（这是一个充分条件，但不是必要条件），对应偏序集也就必有入度为 0 和出度为 0 的节点，dfs 能否一趟遍历就和拓扑排序有关。拓扑排序的零入度起点，可以一趟结束，但是其它的不能一趟结束——非 0 入度节点势必不能一趟做完 dfs，因为根据无环性，它没法转回指向它的节点

推广：全图DFS

//深度优先搜索DFS算法（全图）
template <typename Tv, typename Te>
void Graph<Tv, Te>::dfs( Rank s ) { // s < n
	reset(); Rank clock = 0; //全图复位
	for ( Rank v = s; v < s + n; v++ ) //从s起顺次检查所有顶点
	    if ( UNDISCOVERED == status( v % n ) ) //一旦遇到尚未发现者
	        DFS( v % n, clock ); //即从它出发启动一次DFS
} //如此可完整覆盖全图，且总体复杂度依然保持为O(n+e)

与 bfs 之于 BFS 类似，dfs 也采用邻接表策略，可在累计 O (n+e)时间内，
- 对每一连通/可达分量，从其其实顶点 v 进入 DFS (v)恰好一次，
- 最终生成一个 DFS 森林，包含 c 棵树，n-c 条树边；

DFS-Tree/Forest

从顶点 s 出发的 DFS

在无向图中将访问与 s 连通的所有顶点（connectivity）
在有向图中将访问由 s 可达的所有顶点（reachability）

经 DFS 确定的树边，不会构成回路（回想树是极大无环图）：

从 s 出发的 DFS，将以 s 为根生成一棵 DFS 树；
所有 DFS 树，进而构成 DFS 森林
DFS 树及森林由 parent 指针描述（只不过所有边取反向）

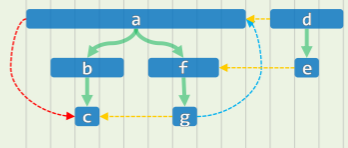
括号引理

在有向图 DFS 的实例中，

若从 a 开始 DFS 可以得到的 DFS-Tree 是这样：
若从 d 开始 DFS，得到的 DFS-Tree 则是这样：

若规定某个节点的活跃期为 $a c t i v e [v] = (d T im e [v], f T im e [v])$ ，表明该节点从发现到访问结束的时间间隔，可以发现，对于有向图 G=(V, E)及其任一 DFS 森林，有：

若 u 是 v 的后代，则 $a c t i v e [u] \subseteq a c t i v e [v]$
若 u 是 v 的祖先，则 $a c t i v e [u] \supseteq a c t i v e [v]$
若 u 与 v 无关，则 $a c t i v e [u] \cap a c t i v e [v] = \emptyset$
这就是括号引理——仅凭 status、dTime 和 fTime 就可以对各边分类；

边分类

何时选用 BFS/DFS？

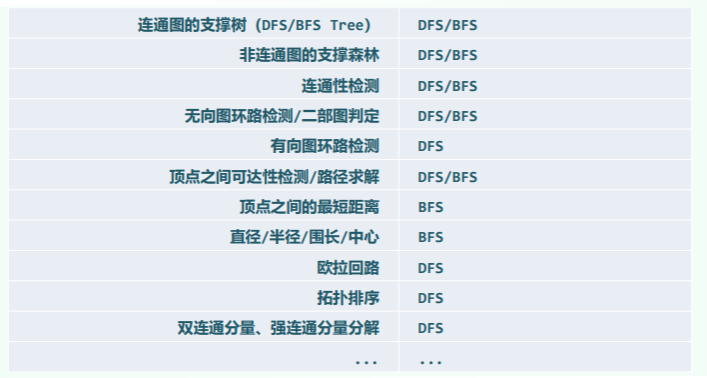
支撑树和支撑森林：都可以
连通性检测：都可以
顶点之间是否可达、路径是什么：都可以
无向图是否存在环路：都可以
- BFS 出现 CROSS 的地方就说明有环路；
- DFS 出现 BACKWARD 也能说明有环路
判断是否是二分图：都可以
- BFS
有向图是否存在环路：只能 DFS，因为 BFS 没有 BACKWARD
- 进一步地，如何判断 BACKWARD 是环路？出现 BACKWARD 就代表出现环路—— 判断目标节点是否 VISITED，即是否是 DAG;
计算图是否构成欧拉回路：DFS 习题解析6-10
给出图的拓扑排序：DFS，方便确定节点是否还有出度
双连通分量、强连通分量的分解：DFS
顶点之间的最短距离：
- BFS，每一层扩散算作 1 个距离，
- 而 DFS 一竿到底难以统计最短距离，只能得到可用的路径，由于访问邻居时比较随机，可能出现各种边，需要进一步讨论处理，比较麻烦；
图的直径、半径、中心、偏心率：这些计算都依赖于最短距离，因此非 BFS 不可；

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索

80-Graph

基本术语

无向图、有向图

路径、环路

支撑树、带权网络

图的存储结构

ADT

邻接矩阵与关联矩阵

邻接矩阵的模板实现

邻接矩阵的静态操作

邻接矩阵的动态操作

邻接矩阵的性能分析

邻接表

空间复杂度

时间复杂度

邻接矩阵与邻接表的取舍原则

十字链表

节点结构

实例

十字链表计算顶点的度

邻接多重表

83-Adjacency-multilist

描述

节点结构

实例

实现

图的遍历

广度优先搜索

思路

实现

实例

推广：全图BFS

性质与应用

边分类

BFS-Tree/Forest

最短路径

Erdős number

Chow Number

二分图

图的偏心率、半径、直径、中心

图/树的直径、偏心率、半径、中心

深度优先搜索

思路

实现

实例

无向图

有向图

推广：全图DFS

DFS-Tree/Forest

括号引理

边分类

何时选用 BFS/DFS？

关系图谱

目录

反向链接