71-BTree

Concept

B-tree is a special type of self-balancing search tree in which each node can contain more than one key and can have more than two children. It is a generalized form of the binary search tree. 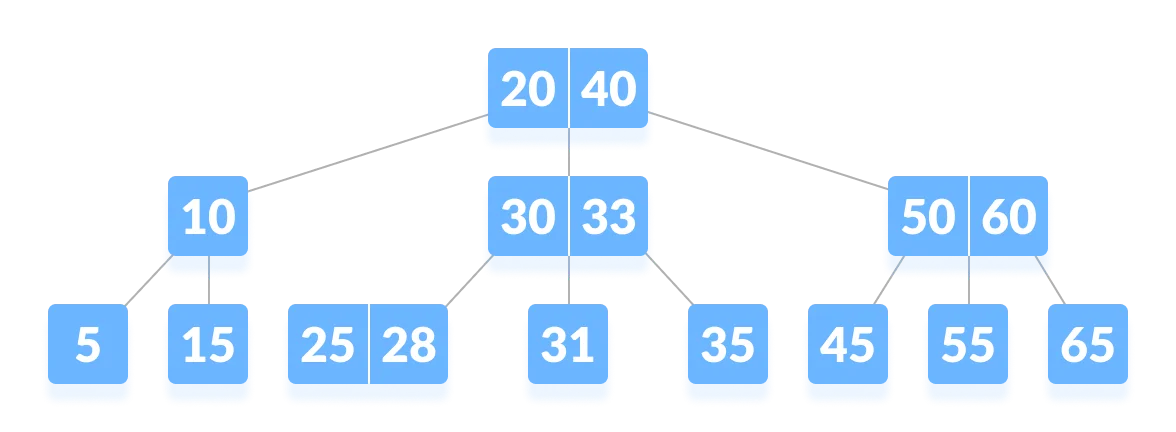It is also known as a height-balanced m-way tree.

Why B-tree?

The need for B-tree arose with the rise in the need for lesser time in accessing physical storage media like a hard disk. The secondary storage devices are slower with a larger capacity. There was a need for such types of data structures that minimize the disk access.

Other data structures such as a binary search tree, avl tree, red-black tree, etc can store only one key in one node. If you have to store a large number of keys, then the height of such trees becomes very large, and the access time increases.

However, B-tree can store many keys in a single node and can have multiple child nodes. This decreases the height significantly allowing faster disk accesses.

B-tree Properties

1. For each node x, the keys are stored in increasing order.
2. In each node, there is a boolean value x.leaf which is true if x is a leaf.
3. If n is the order of the tree, each internal node can contain at most n - 1 keys along with a pointer to each child. （若 B 树阶为 n，则节点内最多 n-1 个键，每个键有指向孩子的指针）
4. Each node except root can have at most n children and at least n/2 children.（多出来的那个指针，指向的孩子中所有键的值，都比原节点的任一键值大）
5. All leaves have the same depth (i.e. height-h of the tree).
6. The root has at least 2 children and contains a minimum of 1 key.
7. If n ≥ 1, then for any n-key B-tree of height h and minimum degree d ≥ 2, $h\ge lo{g}_d\frac{n+1}{2}$ .

B Tree Applications

• databases and file systems
• to store blocks of data (secondary storage media)
• multilevel indexing

Search

Steps

Searching for an element in a B-tree is the generalized form of searching an element in a Binary Search Tree. The following steps are followed.

1. Starting from the root node, compare k with the first key of the node. If k = the first key of the node, return the node and the index.
2. If k.leaf = true, return NULL (i.e. not found).
3. If k < the first key of the root node, search the left child of this key recursively.
4. If there is more than one key in the current node and k > the first key, compare k with the next key in the node.
   • If k < next key, search the left child of this key (ie. k lies in between the first and the second keys).
   • Else, search the right child of the key.
5. Repeat steps 1 to 4 until the leaf is reached.

Example

1. Let us search key k = 17 in the tree below of degree 3.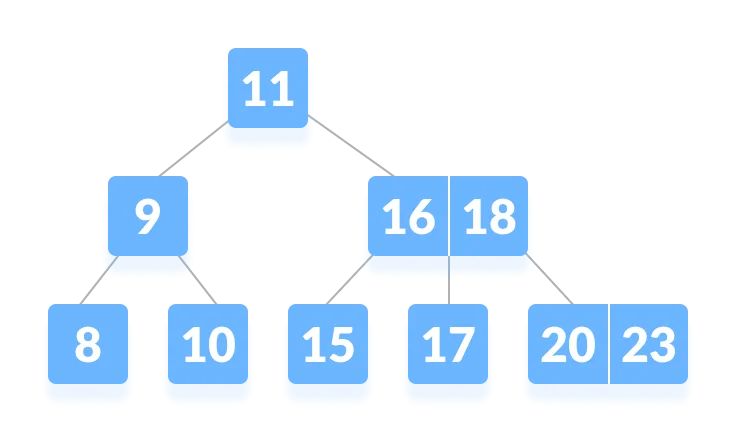
2. k is not found in the root so, compare it with the root key.
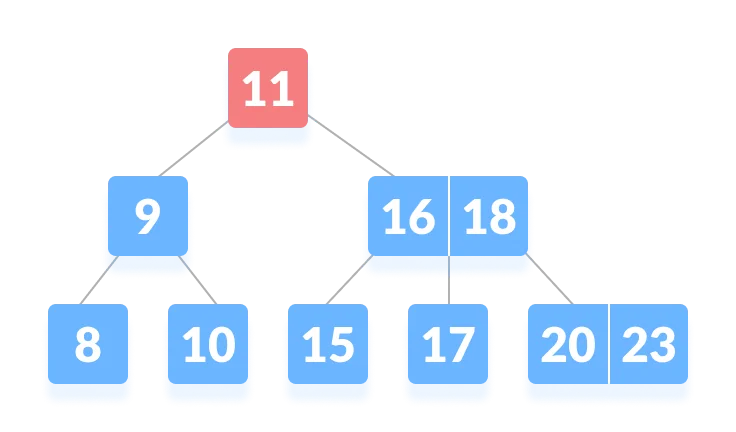
3. Since k > 11, go to the right child of the root node.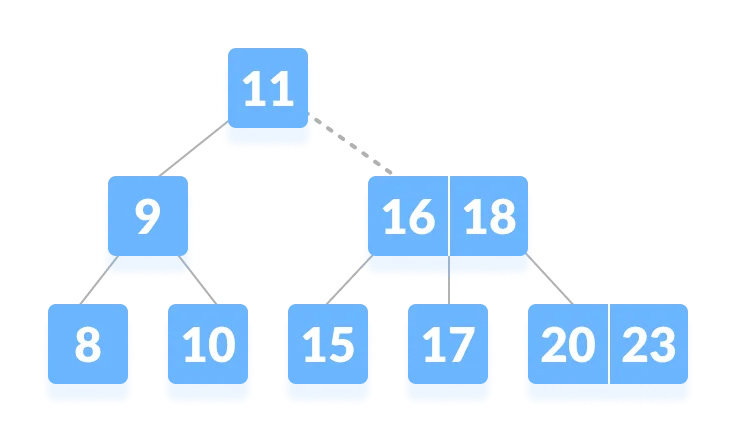
4. Compare k with 16. Since k > 16, compare k with the next key 18.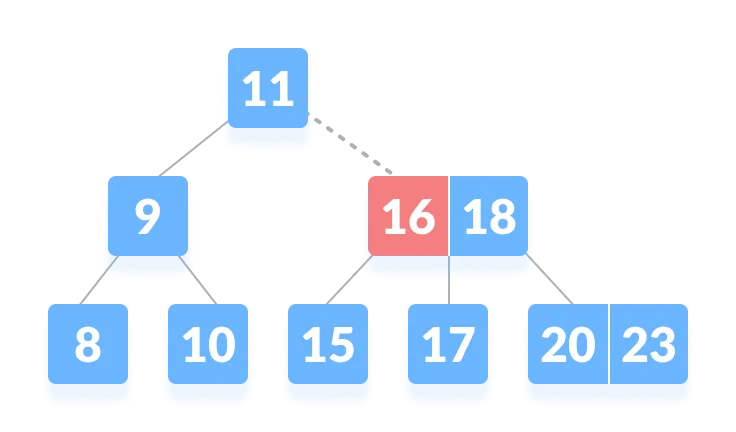
5. Since k < 18, k lies between 16 and 18. Search in the right child of 16 or the left child of 18.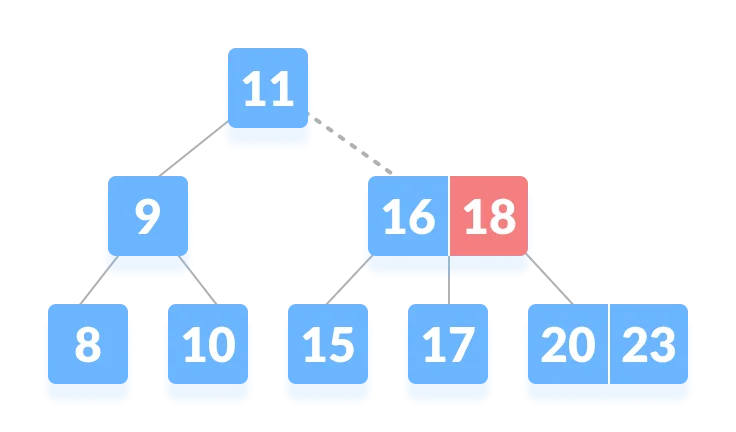
6. k is found.

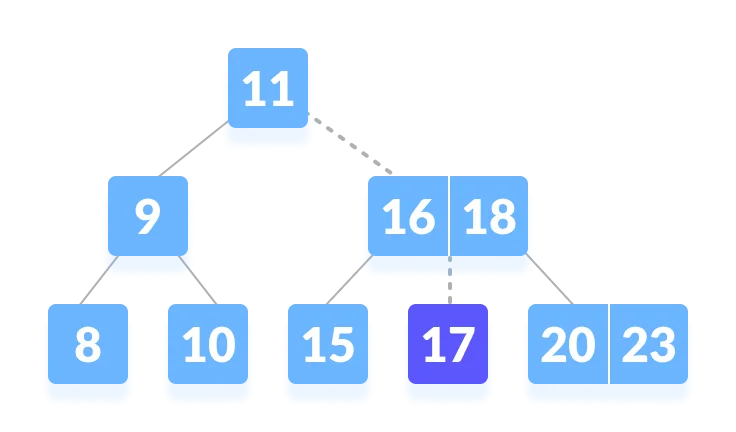
Implementation

Python

# Searching a key on a B-tree in Python
 
 
# Create a node
class BTreeNode:
  def __init__(self, leaf=False):
    self.leaf = leaf
    self.keys = []
    self.child = []
 
 
# Tree
class BTree:
  def __init__(self, t):
    self.root = BTreeNode(True)
    self.t = t
 
    # Insert node
  def insert(self, k):
    root = self.root
    if len(root.keys) == (2 * self.t) - 1:
      temp = BTreeNode()
      self.root = temp
      temp.child.insert(0, root)
      self.split_child(temp, 0)
      self.insert_non_full(temp, k)
    else:
      self.insert_non_full(root, k)
 
    # Insert nonfull
  def insert_non_full(self, x, k):
    i = len(x.keys) - 1
    if x.leaf:
      x.keys.append((None, None))
      while i >= 0 and k[0] < x.keys[i][0]:
        x.keys[i + 1] = x.keys[i]
        i -= 1
      x.keys[i + 1] = k
    else:
      while i >= 0 and k[0] < x.keys[i][0]:
        i -= 1
      i += 1
      if len(x.child[i].keys) == (2 * self.t) - 1:
        self.split_child(x, i)
        if k[0] > x.keys[i][0]:
          i += 1
      self.insert_non_full(x.child[i], k)
 
    # Split the child
  def split_child(self, x, i):
    t = self.t
    y = x.child[i]
    z = BTreeNode(y.leaf)
    x.child.insert(i + 1, z)
    x.keys.insert(i, y.keys[t - 1])
    z.keys = y.keys[t: (2 * t) - 1]
    y.keys = y.keys[0: t - 1]
    if not y.leaf:
      z.child = y.child[t: 2 * t]
      y.child = y.child[0: t - 1]
 
  # Print the tree
  def print_tree(self, x, l=0):
    print("Level ", l, " ", len(x.keys), end=":")
    for i in x.keys:
      print(i, end=" ")
    print()
    l += 1
    if len(x.child) > 0:
      for i in x.child:
        self.print_tree(i, l)
 
  # Search key in the tree
  def search_key(self, k, x=None):
    if x is not None:
      i = 0
      while i < len(x.keys) and k > x.keys[i][0]:
        i += 1
      if i < len(x.keys) and k == x.keys[i][0]:
        return (x, i)
      elif x.leaf:
        return None
      else:
        return self.search_key(k, x.child[i])
      
    else:
      return self.search_key(k, self.root)
 
 
def main():
  B = BTree(3)
 
  for i in range(10):
    B.insert((i, 2 * i))
 
  B.print_tree(B.root)
 
  if B.search_key(8) is not None:
    print("\nFound")
  else:
    print("\nNot Found")
 
 
if __name__ == '__main__':
  main()

Java

// Searching a key on a B-tree in Java 
 
public class BTree {
 
  private int T;
 
  // Node creation
  public class Node {
    int n;
    int key[] = new int[2 * T - 1];
    Node child[] = new Node[2 * T];
    boolean leaf = true;
 
    public int Find(int k) {
      for (int i = 0; i < this.n; i++) {
        if (this.key[i] == k) {
          return i;
        }
      }
      return -1;
    };
  }
 
  public BTree (int t) {
    T = t;
    root = new Node ();
    root. n = 0;
    root. leaf = true;
  }
 
  private Node root;
 
  // Search key
  private Node Search (Node x, int key) {
    int i = 0;
    if (x == null)
      return x;
    for (i = 0; i < x.n; i++) {
      if (key < x.key[i]) {
        break;
      }
      if (key == x.key[i]) {
        return x;
      }
    }
    if (x.leaf) {
      return null;
    } else {
      return Search (x.child[i], key);
    }
  }
 
  // Splitting the node
  private void Split (Node x, int pos, Node y) {
    Node z = new Node ();
    z.leaf = y.leaf;
    z.n = T - 1;
    for (int j = 0; j < T - 1; j++) {
      z.key[j] = y.key[j + T];
    }
    if (!y.leaf) {
      for (int j = 0; j < T; j++) {
        z.child[j] = y.child[j + T];
      }
    }
    y.n = T - 1;
    for (int j = x.n; j >= pos + 1; j--) {
      x.child[j + 1] = x.child[j];
    }
    x.child[pos + 1] = z;
 
    for (int j = x.n - 1; j >= pos; j--) {
      x.key[j + 1] = x.key[j];
    }
    x.key[pos] = y.key[T - 1];
    x.n = x.n + 1;
  }
 
  // Inserting a value
  public void Insert (final int key) {
    Node r = root;
    if (r.n == 2 * T - 1) {
      Node s = new Node ();
      root = s;
      s.leaf = false;
      s.n = 0;
      s.child[0] = r;
      Split (s, 0, r);
      insertValue (s, key);
    } else {
      insertValue (r, key);
    }
  }
 
  // Insert the node
  final private void insertValue (Node x, int k) {
 
    if (x.leaf) {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
        x.key[i + 1] = x.key[i];
      }
      x.key[i + 1] = k;
      x.n = x.n + 1;
    } else {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
      }
      ;
      i++;
      Node tmp = x.child[i];
      if (tmp. n == 2 * T - 1) {
        Split (x, i, tmp);
        if (k > x.key[i]) {
          i++;
        }
      }
      insertValue (x.child[i], k);
    }
 
  }
 
  public void Show () {
    Show (root);
  }
 
  // Display
  private void Show (Node x) {
    assert (x == null);
    for (int i = 0; i < x.n; i++) {
      System.out.print (x.key[i] + " ");
    }
    if (!x.leaf) {
      for (int i = 0; i < x.n + 1; i++) {
        Show (x.child[i]);
      }
    }
  }
 
  // Check if present
  public boolean Contain (int k) {
    if (this.Search (root, k) != null) {
      return true;
    } else {
      return false;
    }
  }
 
  public static void main (String[] args) {
    BTree b = new BTree (3);
    b.Insert (8);
    b.Insert (9);
    b.Insert (10);
    b.Insert (11);
    b.Insert (15);
    b.Insert (20);
    b.Insert (17);
 
    b.Show ();
 
    if (b.Contain (12)) {
      System.out.println ("\nfound");
    } else {
      System.out.println ("\nnot found");
    }
    ;
  }
}

C

// Searching a key on a B-tree in C
 
#include <stdio.h>
#include <stdlib.h>
 
#define MAX 3
#define MIN 2
 
struct BTreeNode {
  int val[MAX + 1], count;
  struct BTreeNode *link[MAX + 1];
};
 
struct BTreeNode *root;
 
// Create a node
struct BTreeNode *createNode (int val, struct BTreeNode *child) {
  struct BTreeNode *newNode;
  newNode = (struct BTreeNode *) malloc (sizeof (struct BTreeNode));
  newNode->val[1] = val;
  newNode->count = 1;
  newNode->link[0] = root;
  newNode->link[1] = child;
  return newNode;
}
 
// Insert node
void insertNode (int val, int pos, struct BTreeNode *node,
        struct BTreeNode *child) {
  int j = node->count;
  while (j > pos) {
    node->val[j + 1] = node->val[j];
    node->link[j + 1] = node->link[j];
    j--;
  }
  node->val[j + 1] = val;
  node->link[j + 1] = child;
  node->count++;
}
 
// Split node
void splitNode (int val, int *pval, int pos, struct BTreeNode *node,
         struct BTreeNode *child, struct BTreeNode **newNode) {
  int median, j;
 
  if (pos > MIN)
    median = MIN + 1;
  else
    median = MIN;
 
  *newNode = (struct BTreeNode *) malloc (sizeof (struct BTreeNode));
  j = median + 1;
  while (j <= MAX) {
    (*newNode)->val[j - median] = node->val[j];
    (*newNode)->link[j - median] = node->link[j];
    j++;
  }
  node->count = median;
  (*newNode)->count = MAX - median;
 
  if (pos <= MIN) {
    insertNode (val, pos, node, child);
  } else {
    insertNode (val, pos - median, *newNode, child);
  }
  *pval = node->val[node->count];
  (*newNode)->link[0] = node->link[node->count];
  node->count--;
}
 
// Set the value
int setValue (int val, int *pval,
           struct BTreeNode *node, struct BTreeNode **child) {
  int pos;
  if (! node) {
    *pval = val;
    *child = NULL;
    return 1;
  }
 
  if (val < node->val[1]) {
    pos = 0;
  } else {
    for (pos = node->count;
       (val < node->val[pos] && pos > 1); pos--)
      ;
    if (val == node->val[pos]) {
      printf ("Duplicates are not permitted\n");
      return 0;
    }
  }
  if (setValue (val, pval, node->link[pos], child)) {
    if (node->count < MAX) {
      insertNode (*pval, pos, node, *child);
    } else {
      splitNode (*pval, pval, pos, node, *child, child);
      return 1;
    }
  }
  return 0;
}
 
// Insert the value
void insert (int val) {
  int flag, i;
  struct BTreeNode *child;
 
  flag = setValue (val, &i, root, &child);
  if (flag)
    root = createNode (i, child);
}
 
// Search node
void search (int val, int *pos, struct BTreeNode *myNode) {
  if (! myNode) {
    return;
  }
 
  if (val < myNode->val[1]) {
    *pos = 0;
  } else {
    for (*pos = myNode->count;
       (val < myNode->val[*pos] && *pos > 1); (*pos)--)
      ;
    if (val == myNode->val[*pos]) {
      printf ("%d is found", val);
      return;
    }
  }
  search (val, pos, myNode->link[*pos]);
 
  return;
}
 
// Traverse then nodes
void traversal (struct BTreeNode *myNode) {
  int i;
  if (myNode) {
    for (i = 0; i < myNode->count; i++) {
      traversal (myNode->link[i]);
      printf ("%d ", myNode->val[i + 1]);
    }
    traversal (myNode->link[i]);
  }
}
 
int main () {
  int val, ch;
 
  insert (8);
  insert (9);
  insert (10);
  insert (11);
  insert (15);
  insert (16);
  insert (17);
  insert (18);
  insert (20);
  insert (23);
 
  traversal (root);
 
  printf ("\n");
  search (11, &ch, root);
}

Cpp

// Searching a key on a B-tree in C++
 
#include <iostream>
using namespace std;
 
class TreeNode {
  int *keys;
  int t;
  TreeNode **C;
  int n;
  bool leaf;
 
   public:
  TreeNode (int temp, bool bool_leaf);
 
  void insertNonFull (int k);
  void splitChild (int i, TreeNode *y);
  void traverse ();
 
  TreeNode *search (int k);
 
  friend class BTree;
};
 
class BTree {
  TreeNode *root;
  int t;
 
   public:
  BTree (int temp) {
    root = NULL;
    t = temp;
  }
 
  void traverse () {
    if (root != NULL)
      root->traverse ();
  }
 
  TreeNode *search (int k) {
    return (root == NULL) ? NULL : root->search (k);
  }
 
  void insert (int k);
};
 
TreeNode:: TreeNode (int t1, bool leaf1) {
  t = t1;
  leaf = leaf1;
 
  keys = new int[2 * t - 1];
  C = new TreeNode *[2 * t];
 
  n = 0;
}
 
void TreeNode:: traverse () {
  int i;
  for (i = 0; i < n; i++) {
    if (leaf == false)
      C[i]->traverse ();
    cout << " " << keys[i];
  }
 
  if (leaf == false)
    C[i]->traverse ();
}
 
TreeNode *TreeNode:: search (int k) {
  int i = 0;
  while (i < n && k > keys[i])
    i++;
 
  if (keys[i] == k)
    return this;
 
  if (leaf == true)
    return NULL;
 
  return C[i]->search (k);
}
 
void BTree:: insert (int k) {
  if (root == NULL) {
    root = new TreeNode (t, true);
    root->keys[0] = k;
    root->n = 1;
  } else {
    if (root->n == 2 * t - 1) {
      TreeNode *s = new TreeNode (t, false);
 
      s->C[0] = root;
 
      s->splitChild (0, root);
 
      int i = 0;
      if (s->keys[0] < k)
        i++;
      s->C[i]->insertNonFull (k);
 
      root = s;
    } else
      root->insertNonFull (k);
  }
}
 
void TreeNode:: insertNonFull (int k) {
  int i = n - 1;
 
  if (leaf == true) {
    while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
    }
 
    keys[i + 1] = k;
    n = n + 1;
  } else {
    while (i >= 0 && keys[i] > k)
      i--;
 
    if (C[i + 1]->n == 2 * t - 1) {
      splitChild (i + 1, C[i + 1]);
 
      if (keys[i + 1] < k)
        i++;
    }
    C[i + 1]->insertNonFull (k);
  }
}
 
void TreeNode:: splitChild (int i, TreeNode *y) {
  TreeNode *z = new TreeNode (y->t, y->leaf);
  z->n = t - 1;
 
  for (int j = 0; j < t - 1; j++)
    z->keys[j] = y->keys[j + t];
 
  if (y->leaf == false) {
    for (int j = 0; j < t; j++)
      z->C[j] = y->C[j + t];
  }
 
  y->n = t - 1;
  for (int j = n; j >= i + 1; j--)
    C[j + 1] = C[j];
 
  C[i + 1] = z;
 
  for (int j = n - 1; j >= i; j--)
    keys[j + 1] = keys[j];
 
  keys[i] = y->keys[t - 1];
  n = n + 1;
}
 
int main () {
  BTree t (3);
  t.insert (8);
  t.insert (9);
  t.insert (10);
  t.insert (11);
  t.insert (15);
  t.insert (16);
  t.insert (17);
  t.insert (18);
  t.insert (20);
  t.insert (23);
 
  cout << "The B-tree is: ";
  t.traverse ();
 
  int k = 10;
  (t.search (k) != NULL) ? cout << endl
                 << k << " is found"
              : cout << endl
                 << k << " is not Found";
 
  k = 2;
  (t.search (k) != NULL) ? cout << endl
                 << k << " is found"
              : cout << endl
                 << k << " is not Found\n";
}

Complexity

• Worst case Time complexity: Θ(log n)
• Average case Time complexity: Θ(log n)
• Best case Time complexity: Θ(log n)
• Average case Space complexity: Θ(n)
• Worst case Space complexity: Θ(n)

Insert

Inserting an element on a B-tree consists of two events: searching the appropriate node to insert the element and splitting the node if required. Insertion operation always takes place in the bottom-up approach.

Let us understand these events below.

Steps

Search if the key has been in B-tree:

1. If the tree is empty, allocate a root node and insert the key.
2. Update the allowed number of keys in the node.
3. Search the appropriate node for insertion.
4. If the node is full, follow the steps below.

If not, insert it:

1. Insert the elements in increasing order.
2. Now, there are elements greater than its limit. So, split at the median.
3. Push the median key upwards and make the left keys as a left child and the right keys as a right child.
4. If the node is not full, follow the steps below.
5. Insert the node in increasing order.

Insert-Example

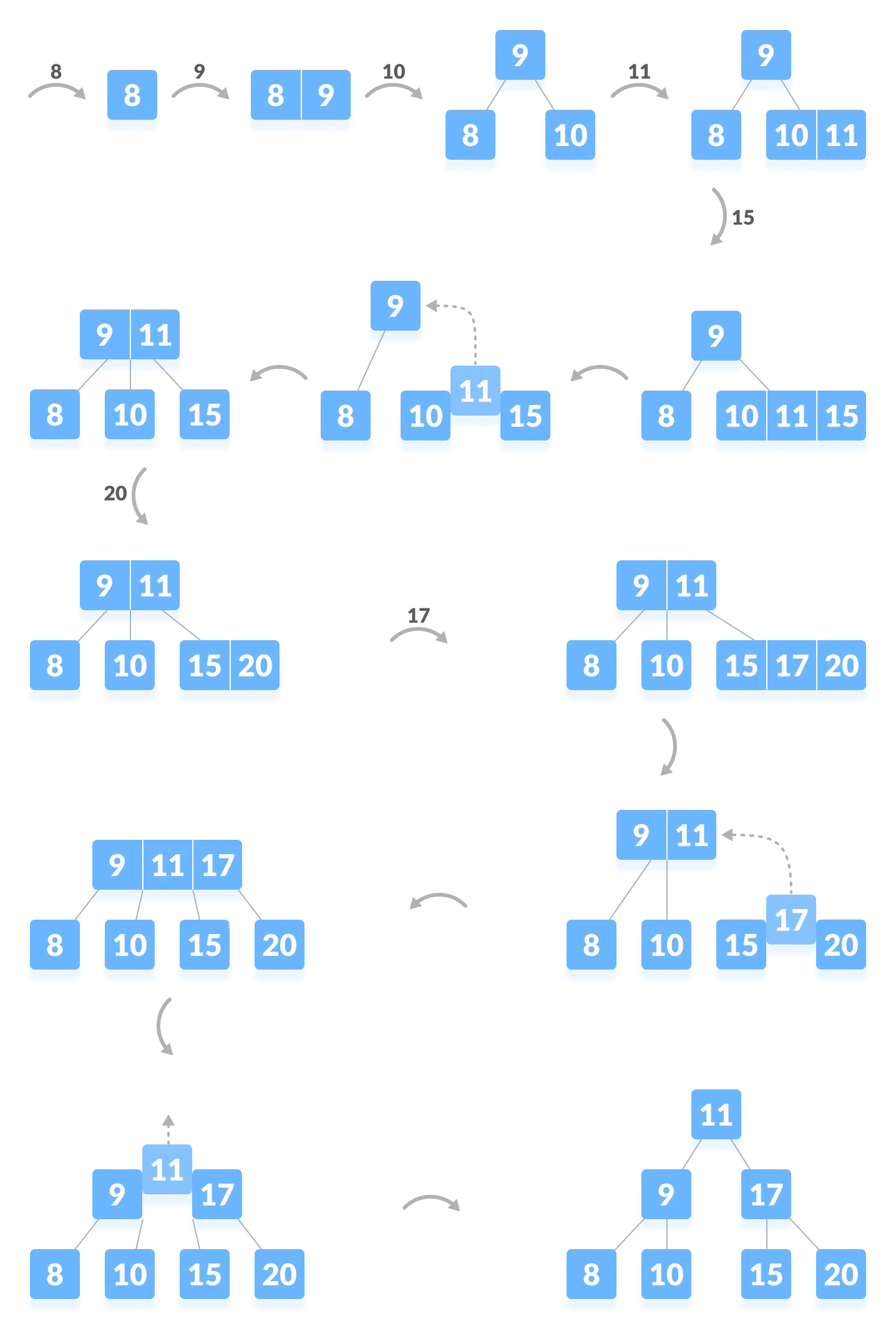
Implementation

Python

# Inserting a key on a B-tree in Python
 
 
# Create a node
class BTreeNode:
    def __init__(self, leaf=False):
        self. leaf = leaf
        self. keys = []
        self. child = []
 
 
# Tree
class BTree:
    def __init__(self, t):
        self. root = BTreeNode (True)
        self. t = t
 
    # Insert node
    def insert (self, k):
        root = self. root
        if len (root. keys) == (2 * self. t) - 1:
            temp = BTreeNode ()
            self. root = temp
            temp. child. insert (0, root)
            self. split_child (temp, 0)
            self. insert_non_full (temp, k)
        else:
            self. insert_non_full (root, k)
 
    # Insert nonfull
    def insert_non_full (self, x, k):
        i = len (x.keys) - 1
        if x.leaf:
            x.keys. append ((None, None))
            while i >= 0 and k[0] < x.keys[i][0]:
                x.keys[i + 1] = x.keys[i]
                i -= 1
            x.keys[i + 1] = k
        else:
            while i >= 0 and k[0] < x.keys[i][0]:
                i -= 1
            i += 1
            if len (x.child[i]. keys) == (2 * self. t) - 1:
                self. split_child (x, i)
                if k[0] > x.keys[i][0]:
                    i += 1
            self. insert_non_full (x.child[i], k)
 
    # Split the child
    def split_child (self, x, i):
        t = self. t
        y = x.child[i]
        z = BTreeNode (y.leaf)
        x.child. insert (i + 1, z)
        x.keys. insert (i, y.keys[t - 1])
        z.keys = y.keys[t: (2 * t) - 1]
        y.keys = y.keys[0: t - 1]
        if not y.leaf:
            z.child = y.child[t: 2 * t]
            y.child = y.child[0: t - 1]
 
    # Print the tree
    def print_tree (self, x, l=0):
        print ("Level ", l, " ", len (x.keys), end=": ")
        for i in x.keys:
            print (i, end=" ")
        print ()
        l += 1
        if len (x.child) > 0:
            for i in x.child:
                self. print_tree (i, l)
 
 
def main ():
    B = BTree (3)
 
    for i in range (10):
        B.insert ((i, 2 * i))
 
    B.print_tree (B.root)
 
 
if __name__ == '__main__':
    main ()

Java

// Inserting a key on a B-tree in Java 
 
public class BTree {
 
  private int T;
 
  // Node Creation
  public class Node {
    int n;
    int key[] = new int[2 * T - 1];
    Node child[] = new Node[2 * T];
    boolean leaf = true;
 
    public int Find (int k) {
      for (int i = 0; i < this. n; i++) {
        if (this. key[i] == k) {
          return i;
        }
      }
      return -1;
    };
  }
 
  public BTree (int t) {
    T = t;
    root = new Node ();
    root. n = 0;
    root. leaf = true;
  }
 
  private Node root;
 
  // split
  private void split (Node x, int pos, Node y) {
    Node z = new Node ();
    z.leaf = y.leaf;
    z.n = T - 1;
    for (int j = 0; j < T - 1; j++) {
      z.key[j] = y.key[j + T];
    }
    if (!y.leaf) {
      for (int j = 0; j < T; j++) {
        z.child[j] = y.child[j + T];
      }
    }
    y.n = T - 1;
    for (int j = x.n; j >= pos + 1; j--) {
      x.child[j + 1] = x.child[j];
    }
    x.child[pos + 1] = z;
 
    for (int j = x.n - 1; j >= pos; j--) {
      x.key[j + 1] = x.key[j];
    }
    x.key[pos] = y.key[T - 1];
    x.n = x.n + 1;
  }
 
  // insert key
  public void insert (final int key) {
    Node r = root;
    if (r.n == 2 * T - 1) {
      Node s = new Node ();
      root = s;
      s.leaf = false;
      s.n = 0;
      s.child[0] = r;
      split (s, 0, r);
      _insert (s, key);
    } else {
      _insert (r, key);
    }
  }
 
  // insert node
  final private void _insert (Node x, int k) {
 
    if (x.leaf) {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
        x.key[i + 1] = x.key[i];
      }
      x.key[i + 1] = k;
      x.n = x.n + 1;
    } else {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
      }
      ;
      i++;
      Node tmp = x.child[i];
      if (tmp. n == 2 * T - 1) {
        split (x, i, tmp);
        if (k > x.key[i]) {
          i++;
        }
      }
      _insert (x.child[i], k);
    }
 
  }
 
  public void display () {
    display (root);
  }
 
  // Display the tree
  private void display (Node x) {
    assert (x == null);
    for (int i = 0; i < x.n; i++) {
      System. out. print (x.key[i] + " ");
    }
    if (!x.leaf) {
      for (int i = 0; i < x.n + 1; i++) {
        display (x.child[i]);
      }
    }
  }
 
  public static void main (String[] args) {
    BTree b = new BTree (3);
    b.insert (8);
    b.insert (9);
    b.insert (10);
    b.insert (11);
    b.insert (15);
    b.insert (20);
    b.insert (17);
 
    b.display ();
  }
}

C

// insertioning a key on a B-tree in C
 
#include <stdio.h>
#include <stdlib.h>
 
#define MAX 3
#define MIN 2
 
struct btreeNode {
  int item[MAX + 1], count;
  struct btreeNode *link[MAX + 1];
};
 
struct btreeNode *root;
 
// Node creation
struct btreeNode *createNode (int item, struct btreeNode *child) {
  struct btreeNode *newNode;
  newNode = (struct btreeNode *) malloc (sizeof (struct btreeNode));
  newNode->item[1] = item;
  newNode->count = 1;
  newNode->link[0] = root;
  newNode->link[1] = child;
  return newNode;
}
 
// Insert
void insertValue (int item, int pos, struct btreeNode *node,
          struct btreeNode *child) {
  int j = node->count;
  while (j > pos) {
    node->item[j + 1] = node->item[j];
    node->link[j + 1] = node->link[j];
    j--;
  }
  node->item[j + 1] = item;
  node->link[j + 1] = child;
  node->count++;
}
 
// Split node
void splitNode (int item, int *pval, int pos, struct btreeNode *node,
         struct btreeNode *child, struct btreeNode **newNode) {
  int median, j;
 
  if (pos > MIN)
    median = MIN + 1;
  else
    median = MIN;
 
  *newNode = (struct btreeNode *) malloc (sizeof (struct btreeNode));
  j = median + 1;
  while (j <= MAX) {
    (*newNode)->item[j - median] = node->item[j];
    (*newNode)->link[j - median] = node->link[j];
    j++;
  }
  node->count = median;
  (*newNode)->count = MAX - median;
 
  if (pos <= MIN) {
    insertValue (item, pos, node, child);
  } else {
    insertValue (item, pos - median, *newNode, child);
  }
  *pval = node->item[node->count];
  (*newNode)->link[0] = node->link[node->count];
  node->count--;
}
 
// Set the value of node
int setNodeValue (int item, int *pval,
           struct btreeNode *node, struct btreeNode **child) {
  int pos;
  if (! node) {
    *pval = item;
    *child = NULL;
    return 1;
  }
 
  if (item < node->item[1]) {
    pos = 0;
  } else {
    for (pos = node->count;
       (item < node->item[pos] && pos > 1); pos--)
      ;
    if (item == node->item[pos]) {
      printf ("Duplicates not allowed\n");
      return 0;
    }
  }
  if (setNodeValue (item, pval, node->link[pos], child)) {
    if (node->count < MAX) {
      insertValue (*pval, pos, node, *child);
    } else {
      splitNode (*pval, pval, pos, node, *child, child);
      return 1;
    }
  }
  return 0;
}
 
// Insert the value
void insertion (int item) {
  int flag, i;
  struct btreeNode *child;
 
  flag = setNodeValue (item, &i, root, &child);
  if (flag)
    root = createNode (i, child);
}
 
// Copy the successor
void copySuccessor (struct btreeNode *myNode, int pos) {
  struct btreeNode *dummy;
  dummy = myNode->link[pos];
 
  for (; dummy->link[0] != NULL;)
    dummy = dummy->link[0];
  myNode->item[pos] = dummy->item[1];
}
 
// Do rightshift
void rightShift (struct btreeNode *myNode, int pos) {
  struct btreeNode *x = myNode->link[pos];
  int j = x->count;
 
  while (j > 0) {
    x->item[j + 1] = x->item[j];
    x->link[j + 1] = x->link[j];
  }
  x->item[1] = myNode->item[pos];
  x->link[1] = x->link[0];
  x->count++;
 
  x = myNode->link[pos - 1];
  myNode->item[pos] = x->item[x->count];
  myNode->link[pos] = x->link[x->count];
  x->count--;
  return;
}
 
// Do leftshift
void leftShift (struct btreeNode *myNode, int pos) {
  int j = 1;
  struct btreeNode *x = myNode->link[pos - 1];
 
  x->count++;
  x->item[x->count] = myNode->item[pos];
  x->link[x->count] = myNode->link[pos]->link[0];
 
  x = myNode->link[pos];
  myNode->item[pos] = x->item[1];
  x->link[0] = x->link[1];
  x->count--;
 
  while (j <= x->count) {
    x->item[j] = x->item[j + 1];
    x->link[j] = x->link[j + 1];
    j++;
  }
  return;
}
 
// Merge the nodes
void mergeNodes (struct btreeNode *myNode, int pos) {
  int j = 1;
  struct btreeNode *x1 = myNode->link[pos], *x2 = myNode->link[pos - 1];
 
  x2->count++;
  x2->item[x2->count] = myNode->item[pos];
  x2->link[x2->count] = myNode->link[0];
 
  while (j <= x1->count) {
    x2->count++;
    x2->item[x2->count] = x1->item[j];
    x2->link[x2->count] = x1->link[j];
    j++;
  }
 
  j = pos;
  while (j < myNode->count) {
    myNode->item[j] = myNode->item[j + 1];
    myNode->link[j] = myNode->link[j + 1];
    j++;
  }
  myNode->count--;
  free (x1);
}
 
// Adjust the node
void adjustNode (struct btreeNode *myNode, int pos) {
  if (! pos) {
    if (myNode->link[1]->count > MIN) {
      leftShift (myNode, 1);
    } else {
      mergeNodes (myNode, 1);
    }
  } else {
    if (myNode->count != pos) {
      if (myNode->link[pos - 1]->count > MIN) {
        rightShift (myNode, pos);
      } else {
        if (myNode->link[pos + 1]->count > MIN) {
          leftShift (myNode, pos + 1);
        } else {
          mergeNodes (myNode, pos);
        }
      }
    } else {
      if (myNode->link[pos - 1]->count > MIN)
        rightShift (myNode, pos);
      else
        mergeNodes (myNode, pos);
    }
  }
}
 
// Traverse the tree
void traversal (struct btreeNode *myNode) {
  int i;
  if (myNode) {
    for (i = 0; i < myNode->count; i++) {
      traversal (myNode->link[i]);
      printf ("%d ", myNode->item[i + 1]);
    }
    traversal (myNode->link[i]);
  }
}
 
int main () {
  int item, ch;
 
  insertion (8);
  insertion (9);
  insertion (10);
  insertion (11);
  insertion (15);
  insertion (16);
  insertion (17);
  insertion (18);
  insertion (20);
  insertion (23);
 
  traversal (root);
}

Cpp

// Inserting a key on a B-tree in C++
 
#include <iostream>
using namespace std;
 
class Node {
  int *keys;
  int t;
  Node **C;
  int n;
  bool leaf;
 
   public:
  Node (int _t, bool _leaf);
 
  void insertNonFull (int k);
  void splitChild (int i, Node *y);
  void traverse ();
 
  friend class BTree;
};
 
class BTree {
  Node *root;
  int t;
 
   public:
  BTree (int _t) {
    root = NULL;
    t = _t;
  }
 
  void traverse () {
    if (root != NULL)
      root->traverse ();
  }
 
  void insert (int k);
};
 
Node:: Node (int t1, bool leaf1) {
  t = t1;
  leaf = leaf1;
 
  keys = new int[2 * t - 1];
  C = new Node *[2 * t];
 
  n = 0;
}
 
// Traverse the nodes
void Node:: traverse () {
  int i;
  for (i = 0; i < n; i++) {
    if (leaf == false)
      C[i]->traverse ();
    cout << " " << keys[i];
  }
 
  if (leaf == false)
    C[i]->traverse ();
}
 
// Insert the node
void BTree:: insert (int k) {
  if (root == NULL) {
    root = new Node (t, true);
    root->keys[0] = k;
    root->n = 1;
  } else {
    if (root->n == 2 * t - 1) {
      Node *s = new Node (t, false);
 
      s->C[0] = root;
 
      s->splitChild (0, root);
 
      int i = 0;
      if (s->keys[0] < k)
        i++;
      s->C[i]->insertNonFull (k);
 
      root = s;
    } else
      root->insertNonFull (k);
  }
}
 
// Insert non full condition
void Node:: insertNonFull (int k) {
  int i = n - 1;
 
  if (leaf == true) {
    while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
    }
 
    keys[i + 1] = k;
    n = n + 1;
  } else {
    while (i >= 0 && keys[i] > k)
      i--;
 
    if (C[i + 1]->n == 2 * t - 1) {
      splitChild (i + 1, C[i + 1]);
 
      if (keys[i + 1] < k)
        i++;
    }
    C[i + 1]->insertNonFull (k);
  }
}
 
// split the child
void Node:: splitChild (int i, Node *y) {
  Node *z = new Node (y->t, y->leaf);
  z->n = t - 1;
 
  for (int j = 0; j < t - 1; j++)
    z->keys[j] = y->keys[j + t];
 
  if (y->leaf == false) {
    for (int j = 0; j < t; j++)
      z->C[j] = y->C[j + t];
  }
 
  y->n = t - 1;
  for (int j = n; j >= i + 1; j--)
    C[j + 1] = C[j];
 
  C[i + 1] = z;
 
  for (int j = n - 1; j >= i; j--)
    keys[j + 1] = keys[j];
 
  keys[i] = y->keys[t - 1];
  n = n + 1;
}
 
int main () {
  BTree t (3);
  t.insert (8);
  t.insert (9);
  t.insert (10);
  t.insert (11);
  t.insert (15);
  t.insert (16);
  t.insert (17);
  t.insert (18);
  t.insert (20);
  t.insert (23);
 
  cout << "The B-tree is: ";
  t.traverse ();
}

Complexity

• Best case Time complexity: Θ(log n)，

  • 查找每个节点开头就能确定去向： $O(\log n)$，
  • 且不需要上溢修复 $O(1)$

• Average case Space complexity: Θ(n)

  • 查找时在节点中间才能确定去向： $O(\frac{n}{2})$，
  • 上溢修复 $O(h)=O(\log n)$

• Worst case Space complexity: Θ(n)

  • 查找时在节点最后才能确定去向： $O(n)$，
  • 上溢修复 $O(h)=O(\log n)$

Delete

Deleting an element on a B-tree consists of three main events: searching the node where the key to be deleted exists, deleting the key and balancing the tree if required.

While deleting a tree, a condition called underflow may occur. Underflow occurs when a node contains less than the minimum number of keys it should hold.

Steps

Before going through the steps below, one must know these facts about a B tree of degree m.

1. A node can have a maximum of m children. (i.e. 3)
2. A node can contain a maximum of m - 1 keys. (i.e. 2)
3. A node should have a minimum of ⌈m/2⌉ children. (i.e. 2)
4. A node (except root node) should contain a minimum of ⌈m/2⌉ - 1 keys. (i.e. 1)

There are three main cases for deletion operation in a B tree.

Case I — delete leaf

The key to be deleted lies in the leaf. There are two cases for it.

1. The deletion of the key does not violate the property of the minimum number of keys a node should hold.
   

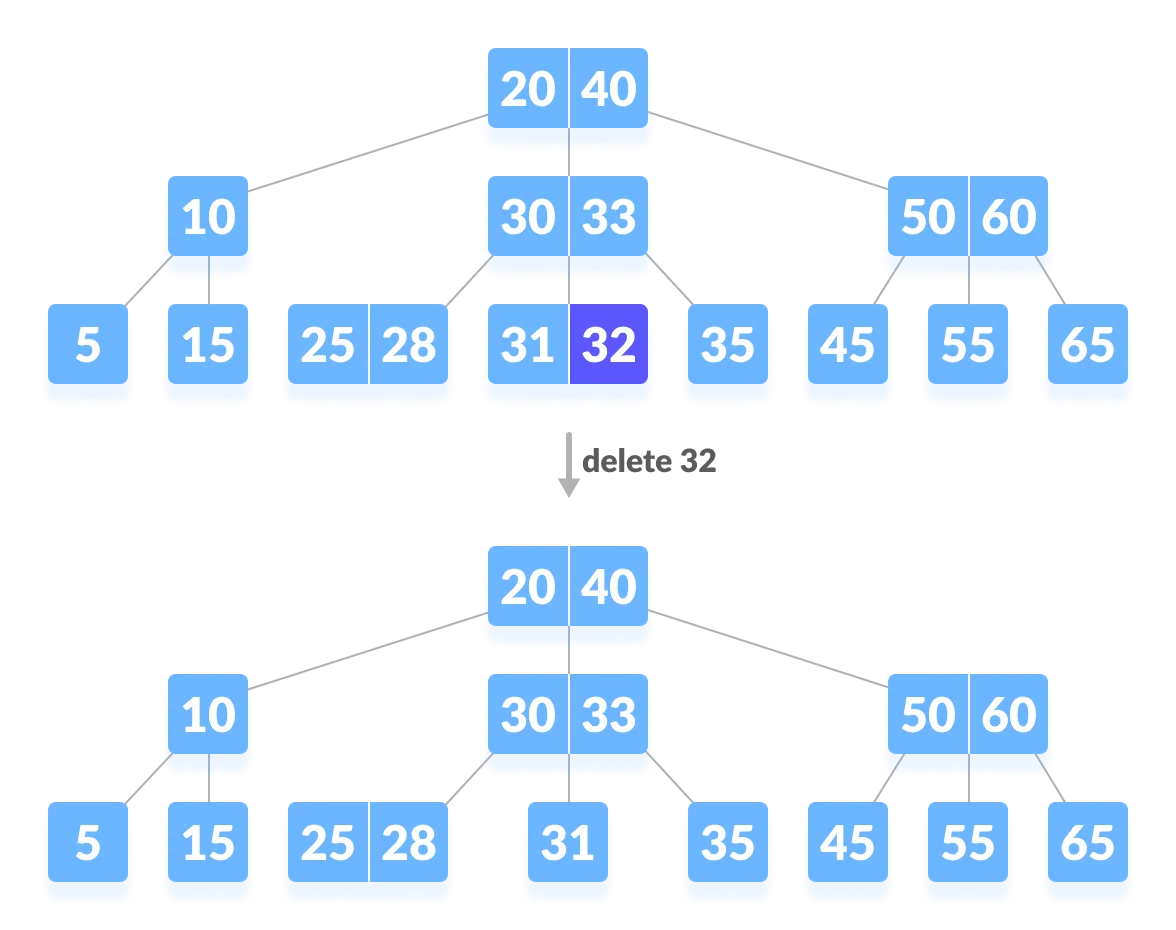
2. The deletion of the key violates the property of the minimum number of keys a node should hold. In this case, we borrow a key from its immediate neighboring sibling node in the order of left to right.

   • First, visit the immediate left sibling. If the left sibling node has more than a minimum number of keys, then borrow a key from this node.
   • Else, check to borrow from the immediate right sibling node.
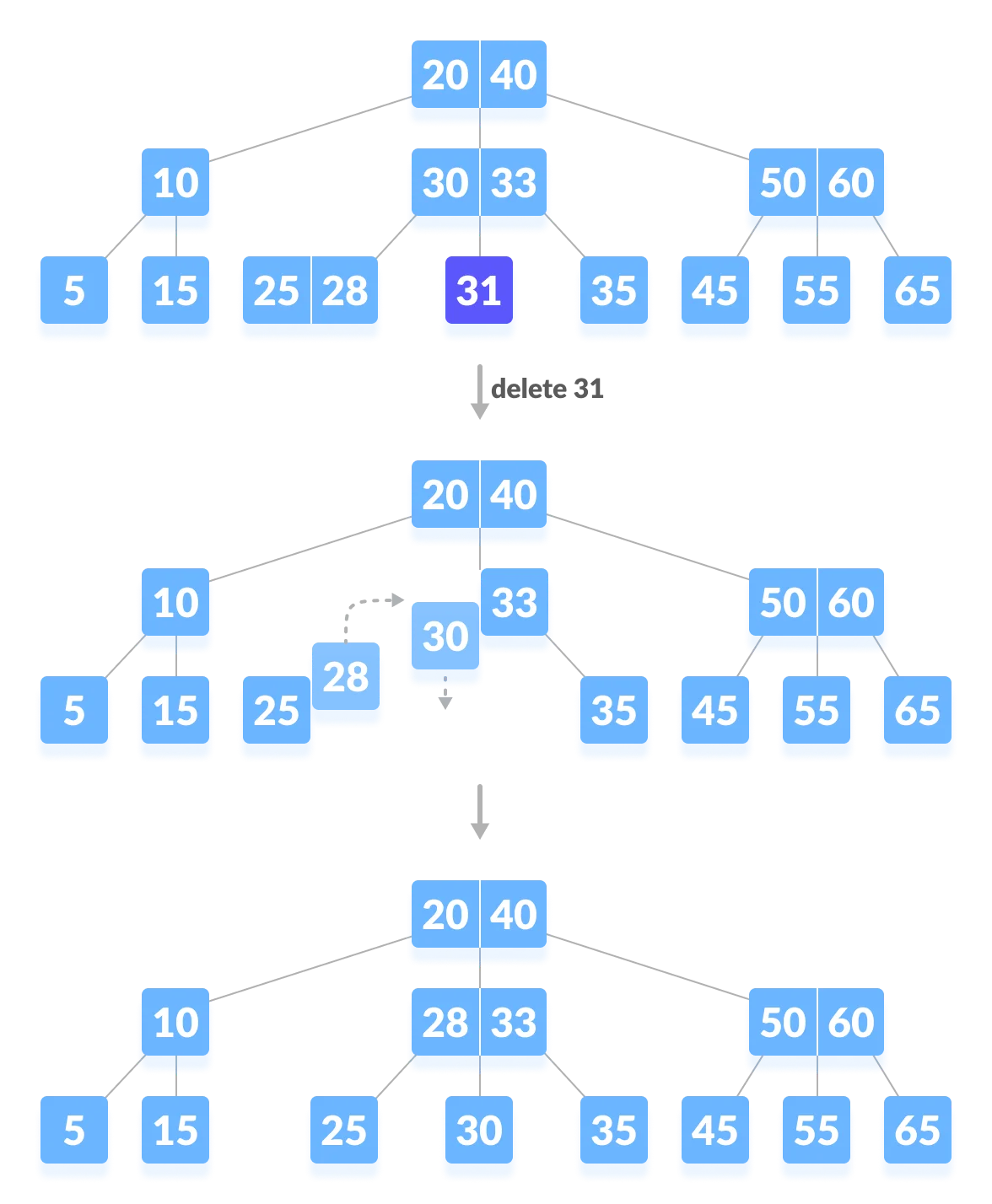
   • If both the immediate sibling nodes already have a minimum number of keys, then merge the node with either the left sibling node or the right sibling node. This merging is done through the parent node.
     

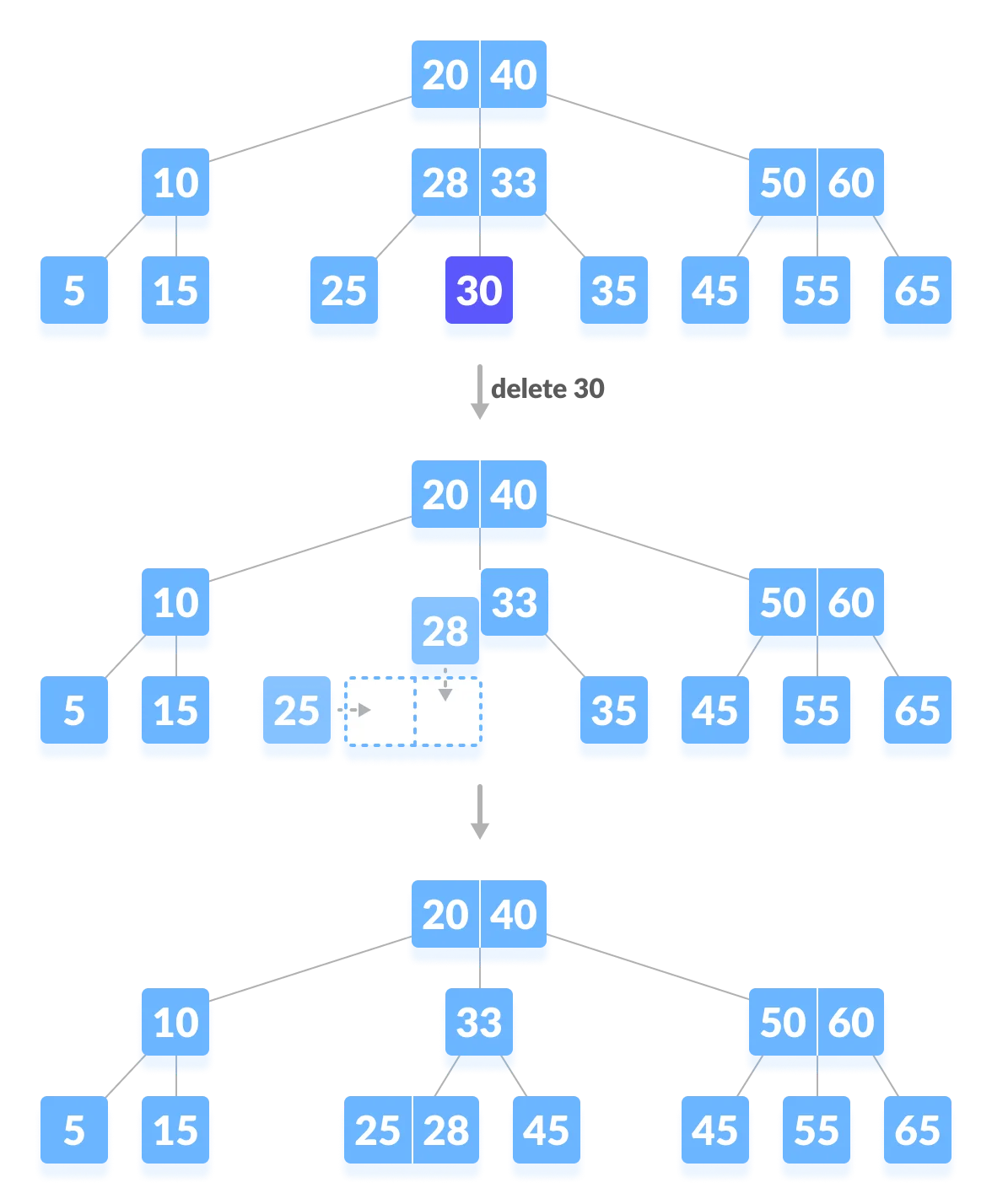
Case II — delete the internals

If the key to be deleted lies in the internal node, the following cases occur.

1. The internal node, which is deleted, is replaced by an inorder predecessor if the left child has more than the minimum number of keys.

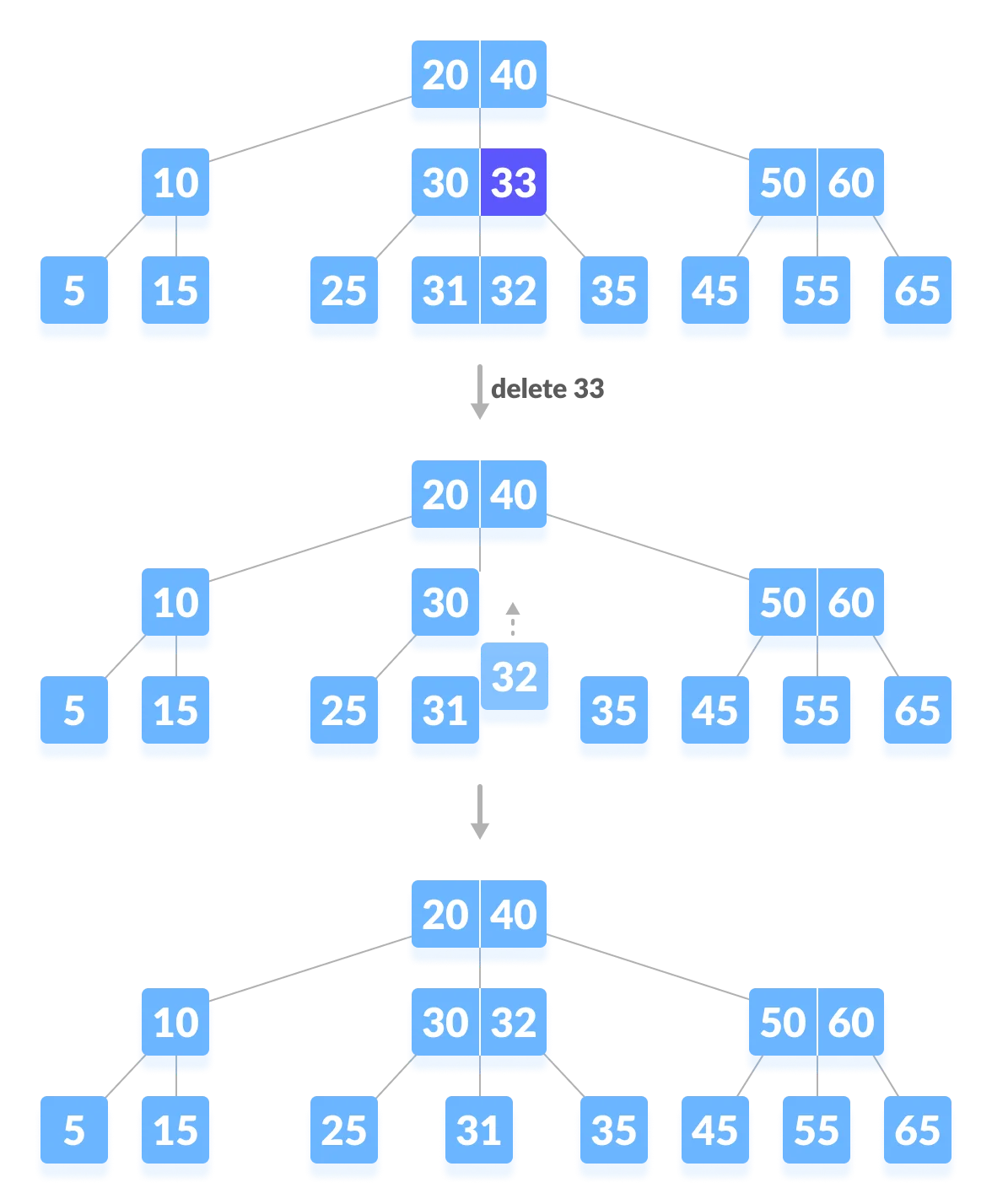
2. The internal node, which is deleted, is replaced by an inorder successor if the right child has more than the minimum number of keys.

3. If either child has exactly a minimum number of keys then, merge the left and the right children.
    

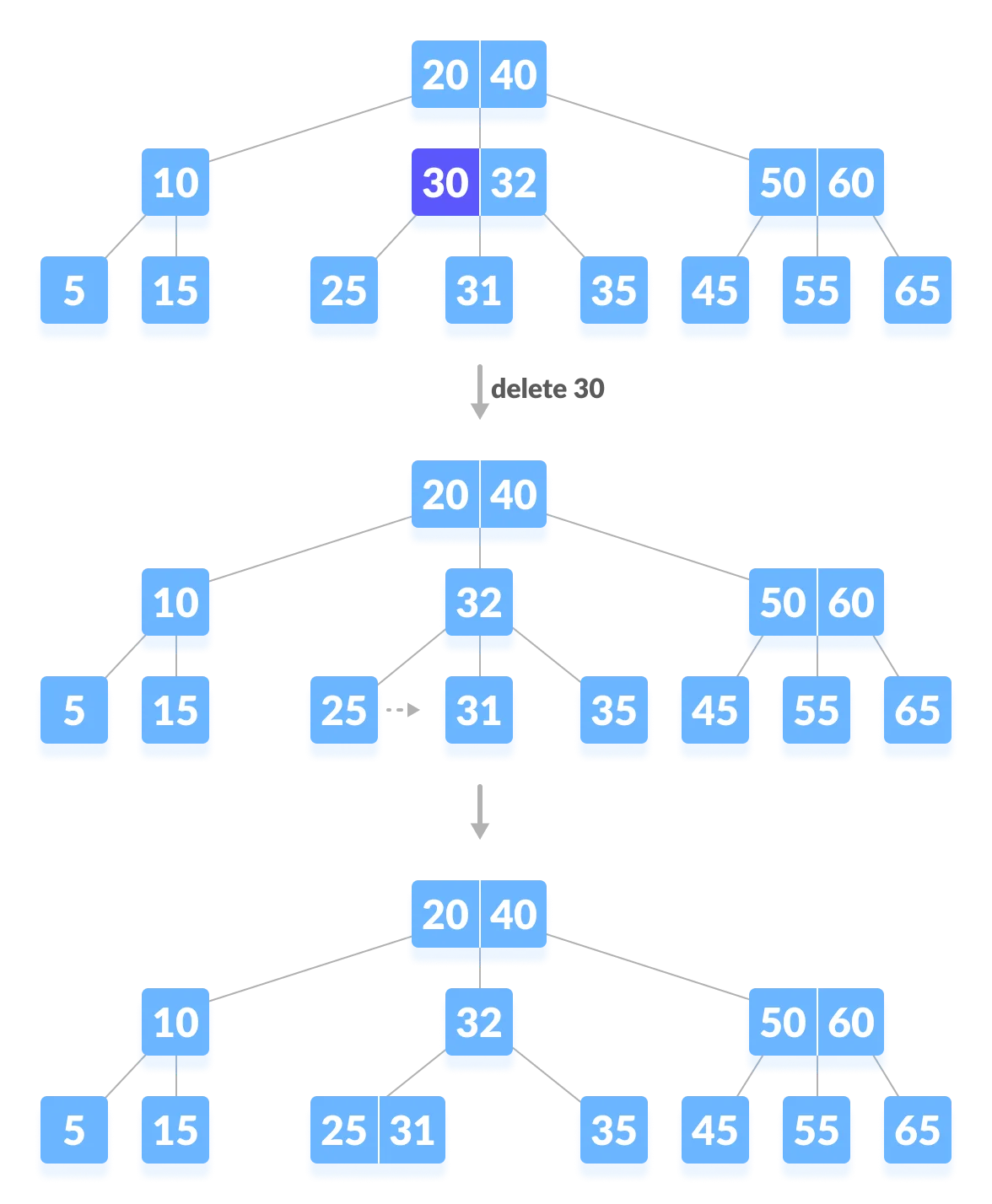
After merging if the parent node has less than the minimum number of keys then, look for the siblings as in Case I.

Case III - shrink height

In this case, the height of the tree shrinks. If the target key lies in an internal node, and the deletion of the key leads to a fewer number of keys in the node (i.e. less than the minimum required), then look for the inorder predecessor and the inorder successor. If both the children contain a minimum number of keys then, borrowing cannot take place. This leads to Case II (3) i.e. merging the children.

Again, look for the sibling to borrow a key. But, if the sibling also has only a minimum number of keys then, merge the node with the sibling along with the parent. Arrange the children accordingly (increasing order).

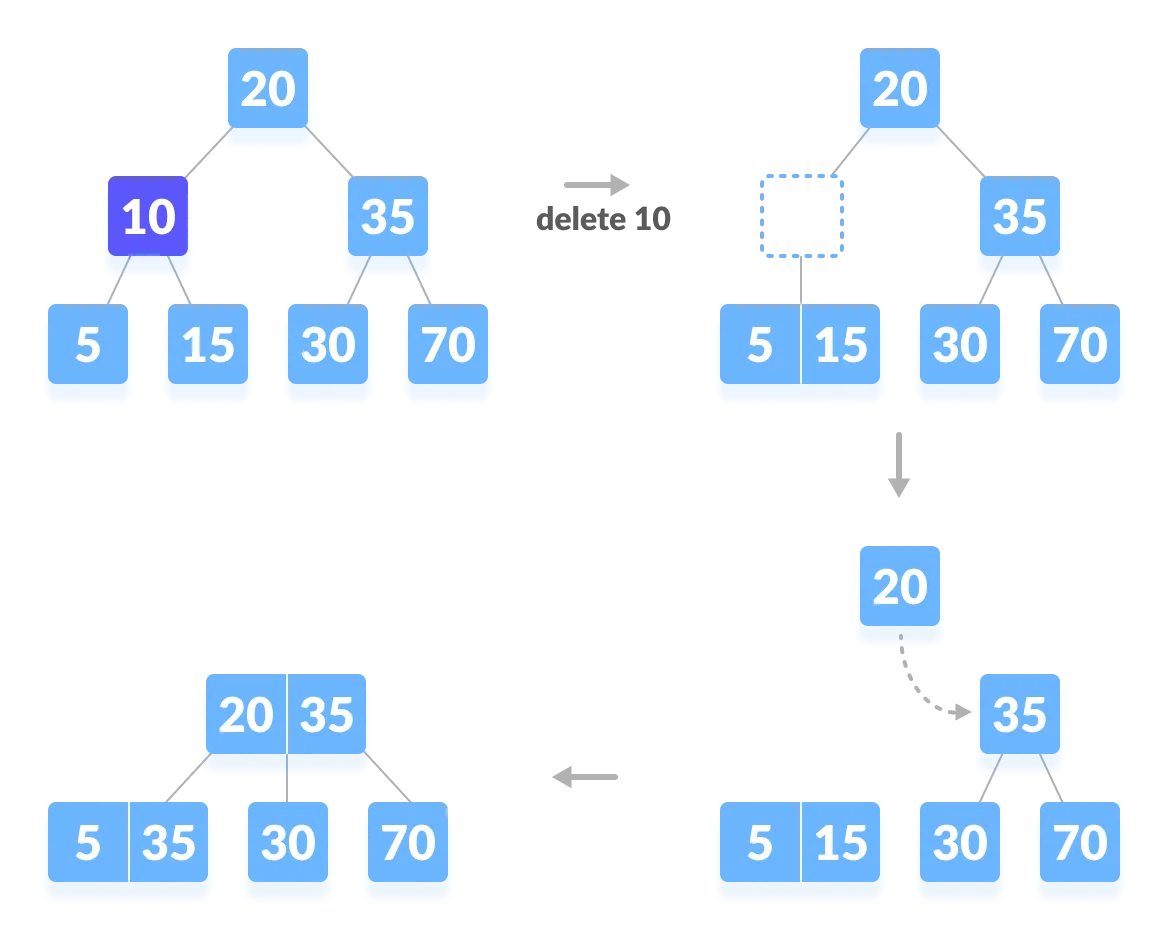
Implementation

Python

# Deleting a key on a B-tree in Python
 
 
# Btree node
class BTreeNode:
    def __init__(self, leaf=False):
        self. leaf = leaf
        self. keys = []
        self. child = []
 
 
class BTree:
    def __init__(self, t):
        self. root = BTreeNode (True)
        self. t = t
 
    # Insert a key
    def insert (self, k):
        root = self. root
        if len (root. keys) == (2 * self. t) - 1:
            temp = BTreeNode ()
            self. root = temp
            temp. child. insert (0, root)
            self. split_child (temp, 0)
            self. insert_non_full (temp, k)
        else:
            self. insert_non_full (root, k)
 
    # Insert non full
    def insert_non_full (self, x, k):
        i = len (x.keys) - 1
        if x.leaf:
            x.keys. append ((None, None))
            while i >= 0 and k[0] < x.keys[i][0]:
                x.keys[i + 1] = x.keys[i]
                i -= 1
            x.keys[i + 1] = k
        else:
            while i >= 0 and k[0] < x.keys[i][0]:
                i -= 1
            i += 1
            if len (x.child[i]. keys) == (2 * self. t) - 1:
                self. split_child (x, i)
                if k[0] > x.keys[i][0]:
                    i += 1
            self. insert_non_full (x.child[i], k)
 
    # Split the child
    def split_child (self, x, i):
        t = self. t
        y = x.child[i]
        z = BTreeNode (y.leaf)
        x.child. insert (i + 1, z)
        x.keys. insert (i, y.keys[t - 1])
        z.keys = y.keys[t: (2 * t) - 1]
        y.keys = y.keys[0: t - 1]
        if not y.leaf:
            z.child = y.child[t: 2 * t]
            y.child = y.child[0: t - 1]
 
    # Delete a node
    def delete (self, x, k):
        t = self. t
        i = 0
        while i < len(x.keys) and k[0] > x.keys[i][0]:
            i += 1
        if x.leaf:
            if i < len (x.keys) and x.keys[i][0] == k[0]:
                x.keys. pop (i)
                return
            return
 
        if i < len (x.keys) and x.keys[i][0] == k[0]:
            return self. delete_internal_node (x, k, i)
        elif len (x.child[i]. keys) >= t:
            self. delete (x.child[i], k)
        else:
            if i != 0 and i + 2 < len (x.child):
                if len (x.child[i - 1]. keys) >= t:
                    self. delete_sibling (x, i, i - 1)
                elif len (x.child[i + 1]. keys) >= t:
                    self. delete_sibling (x, i, i + 1)
                else:
                    self. delete_merge (x, i, i + 1)
            elif i == 0:
                if len (x.child[i + 1]. keys) >= t:
                    self. delete_sibling (x, i, i + 1)
                else:
                    self. delete_merge (x, i, i + 1)
            elif i + 1 == len (x.child):
                if len (x.child[i - 1]. keys) >= t:
                    self. delete_sibling (x, i, i - 1)
                else:
                    self. delete_merge (x, i, i - 1)
            self. delete (x.child[i], k)
 
    # Delete internal node
    def delete_internal_node (self, x, k, i):
        t = self. t
        if x.leaf:
            if x.keys[i][0] == k[0]:
                x.keys. pop (i)
                return
            return
 
        if len (x.child[i]. keys) >= t:
            x.keys[i] = self. delete_predecessor (x.child[i])
            return
        elif len (x.child[i + 1]. keys) >= t:
            x.keys[i] = self. delete_successor (x.child[i + 1])
            return
        else:
            self. delete_merge (x, i, i + 1)
            self. delete_internal_node (x.child[i], k, self. t - 1)
 
    # Delete the predecessor
    def delete_predecessor (self, x):
        if x.leaf:
            return x.pop ()
        n = len (x.keys) - 1
        if len (x.child[n]. keys) >= self. t:
            self. delete_sibling (x, n + 1, n)
        else:
            self. delete_merge (x, n, n + 1)
        self. delete_predecessor (x.child[n])
 
    # Delete the successor
    def delete_successor (self, x):
        if x.leaf:
            return x.keys. pop (0)
        if len (x.child[1]. keys) >= self. t:
            self. delete_sibling (x, 0, 1)
        else:
            self. delete_merge (x, 0, 1)
        self. delete_successor (x.child[0])
 
    # Delete resolution
    def delete_merge (self, x, i, j):
        cnode = x.child[i]
 
        if j > i:
            rsnode = x.child[j]
            cnode. keys. append (x.keys[i])
            for k in range (len (rsnode. keys)):
                cnode. keys. append (rsnode. keys[k])
                if len (rsnode. child) > 0:
                    cnode. child. append (rsnode. child[k])
            if len (rsnode. child) > 0:
                cnode. child. append (rsnode. child. pop ())
            new = cnode
            x.keys. pop (i)
            x.child. pop (j)
        else:
            lsnode = x.child[j]
            lsnode. keys. append (x.keys[j])
            for i in range (len (cnode. keys)):
                lsnode. keys. append (cnode. keys[i])
                if len (lsnode. child) > 0:
                    lsnode. child. append (cnode. child[i])
            if len (lsnode. child) > 0:
                lsnode. child. append (cnode. child. pop ())
            new = lsnode
            x.keys. pop (j)
            x.child. pop (i)
 
        if x == self. root and len (x.keys) == 0:
            self. root = new
 
    # Delete the sibling
    def delete_sibling (self, x, i, j):
        cnode = x.child[i]
        if i < j:
            rsnode = x.child[j]
            cnode. keys. append (x.keys[i])
            x.keys[i] = rsnode. keys[0]
            if len (rsnode. child) > 0:
                cnode. child. append (rsnode. child[0])
                rsnode. child. pop (0)
            rsnode. keys. pop (0)
        else:
            lsnode = x.child[j]
            cnode. keys. insert (0, x.keys[i - 1])
            x.keys[i - 1] = lsnode. keys. pop ()
            if len (lsnode. child) > 0:
                cnode. child. insert (0, lsnode. child. pop ())
 
    # Print the tree
    def print_tree (self, x, l=0):
        print ("Level ", l, " ", len (x.keys), end=": ")
        for i in x.keys:
            print (i, end=" ")
        print ()
        l += 1
        if len (x.child) > 0:
            for i in x.child:
                self. print_tree (i, l)
 
 
 
B = BTree (3)
 
for i in range (10):
    B.insert ((i, 2 * i))
 
B.print_tree (B.root)
 
B.delete (B.root, (8,))
print ("\n")
B.print_tree (B.root)

Java

// Inserting a key on a B-tree in Java
 
import java. util. Stack;
 
public class BTree {
 
  private int T;
 
  public class Node {
    int n;
    int key[] = new int[2 * T - 1];
    Node child[] = new Node[2 * T];
    boolean leaf = true;
 
    public int Find (int k) {
      for (int i = 0; i < this. n; i++) {
        if (this. key[i] == k) {
          return i;
        }
      }
      return -1;
    };
  }
 
  public BTree (int t) {
    T = t;
    root = new Node ();
    root. n = 0;
    root. leaf = true;
  }
 
  private Node root;
 
  // Search the key
  private Node Search (Node x, int key) {
    int i = 0;
    if (x == null)
      return x;
    for (i = 0; i < x.n; i++) {
      if (key < x.key[i]) {
        break;
      }
      if (key == x.key[i]) {
        return x;
      }
    }
    if (x.leaf) {
      return null;
    } else {
      return Search (x.child[i], key);
    }
  }
 
  // Split function
  private void Split (Node x, int pos, Node y) {
    Node z = new Node ();
    z.leaf = y.leaf;
    z.n = T - 1;
    for (int j = 0; j < T - 1; j++) {
      z.key[j] = y.key[j + T];
    }
    if (!y.leaf) {
      for (int j = 0; j < T; j++) {
        z.child[j] = y.child[j + T];
      }
    }
    y.n = T - 1;
    for (int j = x.n; j >= pos + 1; j--) {
      x.child[j + 1] = x.child[j];
    }
    x.child[pos + 1] = z;
 
    for (int j = x.n - 1; j >= pos; j--) {
      x.key[j + 1] = x.key[j];
    }
    x.key[pos] = y.key[T - 1];
    x.n = x.n + 1;
  }
 
  // Insert the key
  public void Insert (final int key) {
    Node r = root;
    if (r.n == 2 * T - 1) {
      Node s = new Node ();
      root = s;
      s.leaf = false;
      s.n = 0;
      s.child[0] = r;
      Split (s, 0, r);
      _Insert (s, key);
    } else {
      _Insert (r, key);
    }
  }
 
  // Insert the node
  final private void _Insert (Node x, int k) {
 
    if (x.leaf) {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
        x.key[i + 1] = x.key[i];
      }
      x.key[i + 1] = k;
      x.n = x.n + 1;
    } else {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
      }
      ;
      i++;
      Node tmp = x.child[i];
      if (tmp. n == 2 * T - 1) {
        Split (x, i, tmp);
        if (k > x.key[i]) {
          i++;
        }
      }
      _Insert (x.child[i], k);
    }
 
  }
 
  public void Show () {
    Show (root);
  }
 
  private void Remove (Node x, int key) {
    int pos = x.Find (key);
    if (pos != -1) {
      if (x.leaf) {
        int i = 0;
        for (i = 0; i < x.n && x.key[i] != key; i++) {
        }
        ;
        for (; i < x.n; i++) {
          if (i != 2 * T - 2) {
            x.key[i] = x.key[i + 1];
          }
        }
        x.n--;
        return;
      }
      if (!x.leaf) {
 
        Node pred = x.child[pos];
        int predKey = 0;
        if (pred. n >= T) {
          for (;;) {
            if (pred. leaf) {
              System. out. println (pred. n);
              predKey = pred. key[pred. n - 1];
              break;
            } else {
              pred = pred. child[pred. n];
            }
          }
          Remove (pred, predKey);
          x.key[pos] = predKey;
          return;
        }
 
        Node nextNode = x.child[pos + 1];
        if (nextNode. n >= T) {
          int nextKey = nextNode. key[0];
          if (! nextNode. leaf) {
            nextNode = nextNode. child[0];
            for (;;) {
              if (nextNode. leaf) {
                nextKey = nextNode. key[nextNode. n - 1];
                break;
              } else {
                nextNode = nextNode. child[nextNode. n];
              }
            }
          }
          Remove (nextNode, nextKey);
          x.key[pos] = nextKey;
          return;
        }
 
        int temp = pred. n + 1;
        pred. key[pred. n++] = x.key[pos];
        for (int i = 0, j = pred. n; i < nextNode. n; i++) {
          pred. key[j++] = nextNode. key[i];
          pred. n++;
        }
        for (int i = 0; i < nextNode. n + 1; i++) {
          pred. child[temp++] = nextNode. child[i];
        }
 
        x.child[pos] = pred;
        for (int i = pos; i < x.n; i++) {
          if (i != 2 * T - 2) {
            x.key[i] = x.key[i + 1];
          }
        }
        for (int i = pos + 1; i < x.n + 1; i++) {
          if (i != 2 * T - 1) {
            x.child[i] = x.child[i + 1];
          }
        }
        x.n--;
        if (x.n == 0) {
          if (x == root) {
            root = x.child[0];
          }
          x = x.child[0];
        }
        Remove (pred, key);
        return;
      }
    } else {
      for (pos = 0; pos < x.n; pos++) {
        if (x.key[pos] > key) {
          break;
        }
      }
      Node tmp = x.child[pos];
      if (tmp. n >= T) {
        Remove (tmp, key);
        return;
      }
      if (true) {
        Node nb = null;
        int devider = -1;
 
        if (pos != x.n && x.child[pos + 1]. n >= T) {
          devider = x.key[pos];
          nb = x.child[pos + 1];
          x.key[pos] = nb. key[0];
          tmp. key[tmp. n++] = devider;
          tmp. child[tmp. n] = nb. child[0];
          for (int i = 1; i < nb. n; i++) {
            nb. key[i - 1] = nb. key[i];
          }
          for (int i = 1; i <= nb. n; i++) {
            nb. child[i - 1] = nb. child[i];
          }
          nb. n--;
          Remove (tmp, key);
          return;
        } else if (pos != 0 && x.child[pos - 1]. n >= T) {
 
          devider = x.key[pos - 1];
          nb = x.child[pos - 1];
          x.key[pos - 1] = nb. key[nb. n - 1];
          Node child = nb. child[nb. n];
          nb. n--;
 
          for (int i = tmp. n; i > 0; i--) {
            tmp. key[i] = tmp. key[i - 1];
          }
          tmp. key[0] = devider;
          for (int i = tmp. n + 1; i > 0; i--) {
            tmp. child[i] = tmp. child[i - 1];
          }
          tmp. child[0] = child;
          tmp. n++;
          Remove (tmp, key);
          return;
        } else {
          Node lt = null;
          Node rt = null;
          boolean last = false;
          if (pos != x.n) {
            devider = x.key[pos];
            lt = x.child[pos];
            rt = x.child[pos + 1];
          } else {
            devider = x.key[pos - 1];
            rt = x.child[pos];
            lt = x.child[pos - 1];
            last = true;
            pos--;
          }
          for (int i = pos; i < x.n - 1; i++) {
            x.key[i] = x.key[i + 1];
          }
          for (int i = pos + 1; i < x.n; i++) {
            x.child[i] = x.child[i + 1];
          }
          x.n--;
          lt. key[lt. n++] = devider;
 
          for (int i = 0, j = lt. n; i < rt. n + 1; i++, j++) {
            if (i < rt. n) {
              lt. key[j] = rt. key[i];
            }
            lt. child[j] = rt. child[i];
          }
          lt. n += rt. n;
          if (x.n == 0) {
            if (x == root) {
              root = x.child[0];
            }
            x = x.child[0];
          }
          Remove (lt, key);
          return;
        }
      }
    }
  }
 
  public void Remove (int key) {
    Node x = Search (root, key);
    if (x == null) {
      return;
    }
    Remove (root, key);
  }
 
  public void Task (int a, int b) {
    Stack<Integer> st = new Stack<>();
    FindKeys (a, b, root, st);
    while (st. isEmpty () == false) {
      this. Remove (root, st. pop ());
    }
  }
 
  private void FindKeys (int a, int b, Node x, Stack<Integer> st) {
    int i = 0;
    for (i = 0; i < x.n && x.key[i] < b; i++) {
      if (x.key[i] > a) {
        st. push (x.key[i]);
      }
    }
    if (!x.leaf) {
      for (int j = 0; j < i + 1; j++) {
        FindKeys (a, b, x.child[j], st);
      }
    }
  }
 
  public boolean Contain (int k) {
    if (this. Search (root, k) != null) {
      return true;
    } else {
      return false;
    }
  }
 
  // Show the node
  private void Show (Node x) {
    assert (x == null);
    for (int i = 0; i < x.n; i++) {
      System. out. print (x.key[i] + " ");
    }
    if (!x.leaf) {
      for (int i = 0; i < x.n + 1; i++) {
        Show (x.child[i]);
      }
    }
  }
 
  public static void main (String[] args) {
    BTree b = new BTree (3);
    b.Insert (8);
    b.Insert (9);
    b.Insert (10);
    b.Insert (11);
    b.Insert (15);
    b.Insert (20);
    b.Insert (17);
 
    b.Show ();
 
    b.Remove (10);
    System. out. println ();
    b.Show ();
  }
}

C

// Deleting a key from a B-tree in C
 
#include <stdio.h>
#include <stdlib.h>
 
#define MAX 3
#define MIN 2
 
struct BTreeNode {
  int item[MAX + 1], count;
  struct BTreeNode *linker[MAX + 1];
};
 
struct BTreeNode *root;
 
// Node creation
struct BTreeNode *createNode (int item, struct BTreeNode *child) {
  struct BTreeNode *newNode;
  newNode = (struct BTreeNode *) malloc (sizeof (struct BTreeNode));
  newNode->item[1] = item;
  newNode->count = 1;
  newNode->linker[0] = root;
  newNode->linker[1] = child;
  return newNode;
}
 
// Add value to the node
void addValToNode (int item, int pos, struct BTreeNode *node,
          struct BTreeNode *child) {
  int j = node->count;
  while (j > pos) {
    node->item[j + 1] = node->item[j];
    node->linker[j + 1] = node->linker[j];
    j--;
  }
  node->item[j + 1] = item;
  node->linker[j + 1] = child;
  node->count++;
}
 
// Split the node
void splitNode (int item, int *pval, int pos, struct BTreeNode *node,
         struct BTreeNode *child, struct BTreeNode **newNode) {
  int median, j;
 
  if (pos > MIN)
    median = MIN + 1;
  else
    median = MIN;
 
  *newNode = (struct BTreeNode *) malloc (sizeof (struct BTreeNode));
  j = median + 1;
  while (j <= MAX) {
    (*newNode)->item[j - median] = node->item[j];
    (*newNode)->linker[j - median] = node->linker[j];
    j++;
  }
  node->count = median;
  (*newNode)->count = MAX - median;
 
  if (pos <= MIN) {
    addValToNode (item, pos, node, child);
  } else {
    addValToNode (item, pos - median, *newNode, child);
  }
  *pval = node->item[node->count];
  (*newNode)->linker[0] = node->linker[node->count];
  node->count--;
}
 
// Set the value in the node
int setValueInNode (int item, int *pval,
           struct BTreeNode *node, struct BTreeNode **child) {
  int pos;
  if (! node) {
    *pval = item;
    *child = NULL;
    return 1;
  }
 
  if (item < node->item[1]) {
    pos = 0;
  } else {
    for (pos = node->count;
       (item < node->item[pos] && pos > 1); pos--)
      ;
    if (item == node->item[pos]) {
      printf ("Duplicates not allowed\n");
      return 0;
    }
  }
  if (setValueInNode (item, pval, node->linker[pos], child)) {
    if (node->count < MAX) {
      addValToNode (*pval, pos, node, *child);
    } else {
      splitNode (*pval, pval, pos, node, *child, child);
      return 1;
    }
  }
  return 0;
}
 
// Insertion operation
void insertion (int item) {
  int flag, i;
  struct BTreeNode *child;
 
  flag = setValueInNode (item, &i, root, &child);
  if (flag)
    root = createNode (i, child);
}
 
// Copy the successor
void copySuccessor (struct BTreeNode *myNode, int pos) {
  struct BTreeNode *dummy;
  dummy = myNode->linker[pos];
 
  for (; dummy->linker[0] != NULL;)
    dummy = dummy->linker[0];
  myNode->item[pos] = dummy->item[1];
}
 
// Remove the value
void removeVal (struct BTreeNode *myNode, int pos) {
  int i = pos + 1;
  while (i <= myNode->count) {
    myNode->item[i - 1] = myNode->item[i];
    myNode->linker[i - 1] = myNode->linker[i];
    i++;
  }
  myNode->count--;
}
 
// Do right shift
void rightShift (struct BTreeNode *myNode, int pos) {
  struct BTreeNode *x = myNode->linker[pos];
  int j = x->count;
 
  while (j > 0) {
    x->item[j + 1] = x->item[j];
    x->linker[j + 1] = x->linker[j];
  }
  x->item[1] = myNode->item[pos];
  x->linker[1] = x->linker[0];
  x->count++;
 
  x = myNode->linker[pos - 1];
  myNode->item[pos] = x->item[x->count];
  myNode->linker[pos] = x->linker[x->count];
  x->count--;
  return;
}
 
// Do left shift
void leftShift (struct BTreeNode *myNode, int pos) {
  int j = 1;
  struct BTreeNode *x = myNode->linker[pos - 1];
 
  x->count++;
  x->item[x->count] = myNode->item[pos];
  x->linker[x->count] = myNode->linker[pos]->linker[0];
 
  x = myNode->linker[pos];
  myNode->item[pos] = x->item[1];
  x->linker[0] = x->linker[1];
  x->count--;
 
  while (j <= x->count) {
    x->item[j] = x->item[j + 1];
    x->linker[j] = x->linker[j + 1];
    j++;
  }
  return;
}
 
// Merge the nodes
void mergeNodes (struct BTreeNode *myNode, int pos) {
  int j = 1;
  struct BTreeNode *x 1 = myNode->linker[pos], *x 2 = myNode->linker[pos - 1];
 
  x 2->count++;
  x 2->item[x 2->count] = myNode->item[pos];
  x 2->linker[x 2->count] = myNode->linker[0];
 
  while (j <= x1->count) {
    x 2->count++;
    x 2->item[x 2->count] = x 1->item[j];
    x 2->linker[x 2->count] = x 1->linker[j];
    j++;
  }
 
  j = pos;
  while (j < myNode->count) {
    myNode->item[j] = myNode->item[j + 1];
    myNode->linker[j] = myNode->linker[j + 1];
    j++;
  }
  myNode->count--;
  free (x 1);
}
 
// Adjust the node
void adjustNode (struct BTreeNode *myNode, int pos) {
  if (! pos) {
    if (myNode->linker[1]->count > MIN) {
      leftShift (myNode, 1);
    } else {
      mergeNodes (myNode, 1);
    }
  } else {
    if (myNode->count != pos) {
      if (myNode->linker[pos - 1]->count > MIN) {
        rightShift (myNode, pos);
      } else {
        if (myNode->linker[pos + 1]->count > MIN) {
          leftShift (myNode, pos + 1);
        } else {
          mergeNodes (myNode, pos);
        }
      }
    } else {
      if (myNode->linker[pos - 1]->count > MIN)
        rightShift (myNode, pos);
      else
        mergeNodes (myNode, pos);
    }
  }
}
 
// Delete a value from the node
int delValFromNode (int item, struct BTreeNode *myNode) {
  int pos, flag = 0;
  if (myNode) {
    if (item < myNode->item[1]) {
      pos = 0;
      flag = 0;
    } else {
      for (pos = myNode->count; (item < myNode->item[pos] && pos > 1); pos--)
        ;
      if (item == myNode->item[pos]) {
        flag = 1;
      } else {
        flag = 0;
      }
    }
    if (flag) {
      if (myNode->linker[pos - 1]) {
        copySuccessor (myNode, pos);
        flag = delValFromNode (myNode->item[pos], myNode->linker[pos]);
        if (flag == 0) {
          printf ("Given data is not present in B-Tree\n");
        }
      } else {
        removeVal (myNode, pos);
      }
    } else {
      flag = delValFromNode (item, myNode->linker[pos]);
    }
    if (myNode->linker[pos]) {
      if (myNode->linker[pos]->count < MIN)
        adjustNode (myNode, pos);
    }
  }
  return flag;
}
 
// Delete operaiton
void delete (int item, struct BTreeNode *myNode) {
  struct BTreeNode *tmp;
  if (! delValFromNode (item, myNode)) {
    printf ("Not present\n");
    return;
  } else {
    if (myNode->count == 0) {
      tmp = myNode;
      myNode = myNode->linker[0];
      free (tmp);
    }
  }
  root = myNode;
  return;
}
 
void searching (int item, int *pos, struct BTreeNode *myNode) {
  if (! myNode) {
    return;
  }
 
  if (item < myNode->item[1]) {
    *pos = 0;
  } else {
    for (*pos = myNode->count;
       (item < myNode->item[*pos] && *pos > 1); (*pos)--)
      ;
    if (item == myNode->item[*pos]) {
      printf ("%d present in B-tree", item);
      return;
    }
  }
  searching (item, pos, myNode->linker[*pos]);
  return;
}
 
void traversal (struct BTreeNode *myNode) {
  int i;
  if (myNode) {
    for (i = 0; i < myNode->count; i++) {
      traversal (myNode->linker[i]);
      printf ("%d ", myNode->item[i + 1]);
    }
    traversal (myNode->linker[i]);
  }
}
 
int main () {
  int item, ch;
 
  insertion (8);
  insertion (9);
  insertion (10);
  insertion (11);
  insertion (15);
  insertion (16);
  insertion (17);
  insertion (18);
  insertion (20);
  insertion (23);
 
  traversal (root);
 
  delete (20, root);
  printf ("\n");
  traversal (root);
}

Cpp

// Deleting a key from a B-tree in C++
 
#include <iostream>
using namespace std;
 
class BTreeNode {
  int *keys;
  int t;
  BTreeNode **C;
  int n;
  bool leaf;
 
   public:
  BTreeNode (int _t, bool _leaf);
 
  void traverse ();
 
  int findKey (int k);
  void insertNonFull (int k);
  void splitChild (int i, BTreeNode *y);
  void deletion (int k);
  void removeFromLeaf (int idx);
  void removeFromNonLeaf (int idx);
  int getPredecessor (int idx);
  int getSuccessor (int idx);
  void fill (int idx);
  void borrowFromPrev (int idx);
  void borrowFromNext (int idx);
  void merge (int idx);
  friend class BTree;
};
 
class BTree {
  BTreeNode *root;
  int t;
 
   public:
  BTree (int _t) {
    root = NULL;
    t = _t;
  }
 
  void traverse () {
    if (root != NULL)
      root->traverse ();
  }
 
  void insertion (int k);
 
  void deletion (int k);
};
 
// B tree node
BTreeNode:: BTreeNode (int t1, bool leaf1) {
  t = t1;
  leaf = leaf1;
 
  keys = new int[2 * t - 1];
  C = new BTreeNode *[2 * t];
 
  n = 0;
}
 
// Find the key
int BTreeNode:: findKey (int k) {
  int idx = 0;
  while (idx < n && keys[idx] < k)
    ++idx;
  return idx;
}
 
// Deletion operation
void BTreeNode:: deletion (int k) {
  int idx = findKey (k);
 
  if (idx < n && keys[idx] == k) {
    if (leaf)
      removeFromLeaf (idx);
    else
      removeFromNonLeaf (idx);
  } else {
    if (leaf) {
      cout << "The key " << k << " is does not exist in the tree\n";
      return;
    }
 
    bool flag = ((idx == n) ? true : false);
 
    if (C[idx]->n < t)
      fill (idx);
 
    if (flag && idx > n)
      C[idx - 1]->deletion (k);
    else
      C[idx]->deletion (k);
  }
  return;
}
 
// Remove from the leaf
void BTreeNode:: removeFromLeaf (int idx) {
  for (int i = idx + 1; i < n; ++i)
    keys[i - 1] = keys[i];
 
  n--;
 
  return;
}
 
// Delete from non leaf node
void BTreeNode:: removeFromNonLeaf (int idx) {
  int k = keys[idx];
 
  if (C[idx]->n >= t) {
    int pred = getPredecessor (idx);
    keys[idx] = pred;
    C[idx]->deletion (pred);
  }
 
  else if (C[idx + 1]->n >= t) {
    int succ = getSuccessor (idx);
    keys[idx] = succ;
    C[idx + 1]->deletion (succ);
  }
 
  else {
    merge (idx);
    C[idx]->deletion (k);
  }
  return;
}
 
int BTreeNode:: getPredecessor (int idx) {
  BTreeNode *cur = C[idx];
  while (! cur->leaf)
    cur = cur->C[cur->n];
 
  return cur->keys[cur->n - 1];
}
 
int BTreeNode:: getSuccessor (int idx) {
  BTreeNode *cur = C[idx + 1];
  while (! cur->leaf)
    cur = cur->C[0];
 
  return cur->keys[0];
}
 
void BTreeNode:: fill (int idx) {
  if (idx != 0 && C[idx - 1]->n >= t)
    borrowFromPrev (idx);
 
  else if (idx != n && C[idx + 1]->n >= t)
    borrowFromNext (idx);
 
  else {
    if (idx != n)
      merge (idx);
    else
      merge (idx - 1);
  }
  return;
}
 
// Borrow from previous
void BTreeNode:: borrowFromPrev (int idx) {
  BTreeNode *child = C[idx];
  BTreeNode *sibling = C[idx - 1];
 
  for (int i = child->n - 1; i >= 0; --i)
    child->keys[i + 1] = child->keys[i];
 
  if (! child->leaf) {
    for (int i = child->n; i >= 0; --i)
      child->C[i + 1] = child->C[i];
  }
 
  child->keys[0] = keys[idx - 1];
 
  if (! child->leaf)
    child->C[0] = sibling->C[sibling->n];
 
  keys[idx - 1] = sibling->keys[sibling->n - 1];
 
  child->n += 1;
  sibling->n -= 1;
 
  return;
}
 
// Borrow from the next
void BTreeNode:: borrowFromNext (int idx) {
  BTreeNode *child = C[idx];
  BTreeNode *sibling = C[idx + 1];
 
  child->keys[(child->n)] = keys[idx];
 
  if (! (child->leaf))
    child->C[(child->n) + 1] = sibling->C[0];
 
  keys[idx] = sibling->keys[0];
 
  for (int i = 1; i < sibling->n; ++i)
    sibling->keys[i - 1] = sibling->keys[i];
 
  if (! sibling->leaf) {
    for (int i = 1; i <= sibling->n; ++i)
      sibling->C[i - 1] = sibling->C[i];
  }
 
  child->n += 1;
  sibling->n -= 1;
 
  return;
}
 
// Merge
void BTreeNode:: merge (int idx) {
  BTreeNode *child = C[idx];
  BTreeNode *sibling = C[idx + 1];
 
  child->keys[t - 1] = keys[idx];
 
  for (int i = 0; i < sibling->n; ++i)
    child->keys[i + t] = sibling->keys[i];
 
  if (! child->leaf) {
    for (int i = 0; i <= sibling->n; ++i)
      child->C[i + t] = sibling->C[i];
  }
 
  for (int i = idx + 1; i < n; ++i)
    keys[i - 1] = keys[i];
 
  for (int i = idx + 2; i <= n; ++i)
    C[i - 1] = C[i];
 
  child->n += sibling->n + 1;
  n--;
 
  delete (sibling);
  return;
}
 
// Insertion operation
void BTree:: insertion (int k) {
  if (root == NULL) {
    root = new BTreeNode (t, true);
    root->keys[0] = k;
    root->n = 1;
  } else {
    if (root->n == 2 * t - 1) {
      BTreeNode *s = new BTreeNode (t, false);
 
      s->C[0] = root;
 
      s->splitChild (0, root);
 
      int i = 0;
      if (s->keys[0] < k)
        i++;
      s->C[i]->insertNonFull (k);
 
      root = s;
    } else
      root->insertNonFull (k);
  }
}
 
// Insertion non full
void BTreeNode:: insertNonFull (int k) {
  int i = n - 1;
 
  if (leaf == true) {
    while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
    }
 
    keys[i + 1] = k;
    n = n + 1;
  } else {
    while (i >= 0 && keys[i] > k)
      i--;
 
    if (C[i + 1]->n == 2 * t - 1) {
      splitChild (i + 1, C[i + 1]);
 
      if (keys[i + 1] < k)
        i++;
    }
    C[i + 1]->insertNonFull (k);
  }
}
 
// Split child
void BTreeNode:: splitChild (int i, BTreeNode *y) {
  BTreeNode *z = new BTreeNode (y->t, y->leaf);
  z->n = t - 1;
 
  for (int j = 0; j < t - 1; j++)
    z->keys[j] = y->keys[j + t];
 
  if (y->leaf == false) {
    for (int j = 0; j < t; j++)
      z->C[j] = y->C[j + t];
  }
 
  y->n = t - 1;
 
  for (int j = n; j >= i + 1; j--)
    C[j + 1] = C[j];
 
  C[i + 1] = z;
 
  for (int j = n - 1; j >= i; j--)
    keys[j + 1] = keys[j];
 
  keys[i] = y->keys[t - 1];
 
  n = n + 1;
}
 
// Traverse
void BTreeNode:: traverse () {
  int i;
  for (i = 0; i < n; i++) {
    if (leaf == false)
      C[i]->traverse ();
    cout << " " << keys[i];
  }
 
  if (leaf == false)
    C[i]->traverse ();
}
 
// Delete Operation
void BTree:: deletion (int k) {
  if (! root) {
    cout << "The tree is empty\n";
    return;
  }
 
  root->deletion (k);
 
  if (root->n == 0) {
    BTreeNode *tmp = root;
    if (root->leaf)
      root = NULL;
    else
      root = root->C[0];
 
    delete tmp;
  }
  return;
}
 
int main () {
  BTree t (3);
  t.insertion (8);
  t.insertion (9);
  t.insertion (10);
  t.insertion (11);
  t.insertion (15);
  t.insertion (16);
  t.insertion (17);
  t.insertion (18);
  t.insertion (20);
  t.insertion (23);
 
  cout << "The B-tree is: ";
  t.traverse ();
 
  t.deletion (20);
 
  cout << "\nThe B-tree is: ";
  t.traverse ();
}

Complexity

• Best case Time complexity: Θ(log n)
• Average case Space complexity: Θ(n)
• Worst case Space complexity: Θ(n)