Definition of VC Dimension
Probably Learning
上节课我们证明了 ,那么联系 ML 的整个流程,我们可以推断出:对任何 ,在足够大的取样 上,由 Hoeffding 不等式可知,
这告诉我们,如果
- 有一个好的假设集 ,即 会在 处 break ;
- 有一个好的取样 ,即 足够大,那么可以 probably 地认为 ;
- 有一个好的学习算法 ,即 能够取到一个 很小的对目标函数的估计 g ,那么 learning 是 probably 可以做到的,且有意义的。
VC Dimension and Learning
前文中一个关键的概念是 break point ,而此处我们将 VC Dimension 定义为:the formal name of maximum non-break point,即最大的非间断点
- 记作 ,即对假设集 ,其 VC Dimension 为最大的满足 的点,
- 换句话说, ,
- 如此一来,对输入样本数 时,则 能够(不是必然) shatter 个输入中的一部分。
按照上节课的举例,同样对应了四种 VC Dimension:

- 因此,只要 是有限的,那么就称为“好的”、“可行的”、“复杂度足够令人满意”的假设集;
那么,VC Dimension 对 ML 的意义是什么呢?即,只要存在有限大小的 ,那么对目标函数的估计 g 就是可以采用、信任、一般化的:
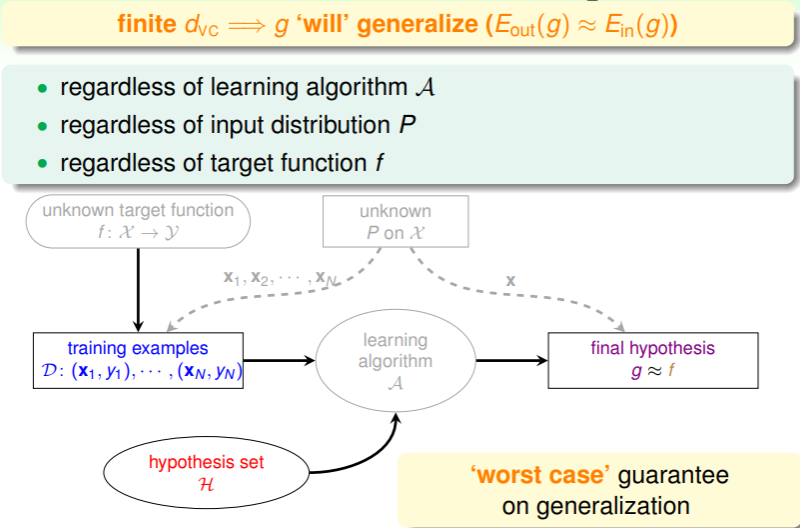
- 不必考虑学习算法(只是影响 的大小而已,但不改变 的事实)、输入的分布情况、目标函数的实际形式等诸多因素,从而证明 ML 是可行的!
练习:理解 VC Dimension

VC Dimension of Perceptrons
回想之前线性划分的 PLA 的问题中,我们通过以下两个方面论证了 ML 的可行性:
- 训练集 是线性可分的,因此 PLA 能够最终停止,即在足够轮次的运行后,能够找到对目标函数 f 的最佳估计 g ,使得 ;
- 如果样本数据服从特定分布 ,并且存在目标函数 f 使得 ,那么由 Hoeffding 不等式及该问题的 可知,当采样数 N 足够大时,有 ,进而 ;
那么,如果在更高维问题上, 又是怎样的?PLA 还能继续有效吗?
Calculate VC Dimension
注意到在 1 维 perceptron (如 postive rays 问题)上 ,在 2 维 perceptron 问题上 (回想是如何证明的?),那么不妨猜测,d 维 perceptron 上 ,要证明之,则可用夹逼法:
-
证明 :
- 首先要确定如何描述这个命题?
 即,只要存在一种 个输入的样例使得 ,就能说明 。
即,只要存在一种 个输入的样例使得 ,就能说明 。 - 因此接下来考虑一种特殊情形:
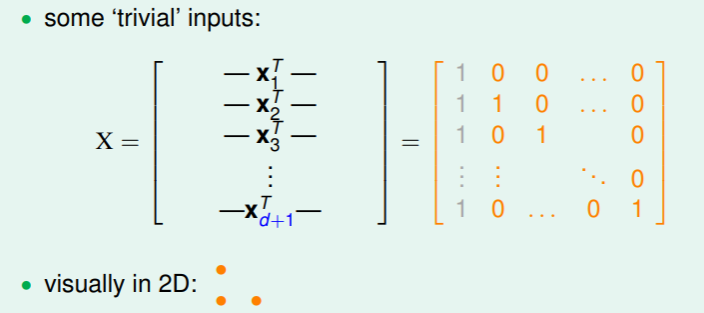 这个矩阵 是可逆的,要使其可被长度为 的向量 shatter ,即对任何 ,找到对应的 能够满足 ,即能够说明这样一个特殊的矩阵 能够实现 的要求;
这个矩阵 是可逆的,要使其可被长度为 的向量 shatter ,即对任何 ,找到对应的 能够满足 ,即能够说明这样一个特殊的矩阵 能够实现 的要求;
- 首先要确定如何描述这个命题?
-
证明 :
- 同样的,这个命题要如何描述?
 与证明 ≥ 不同,此处要求任何 长度的输入都无法 shatter。
与证明 ≥ 不同,此处要求任何 长度的输入都无法 shatter。 - 我们以下面一个特殊例子说明:
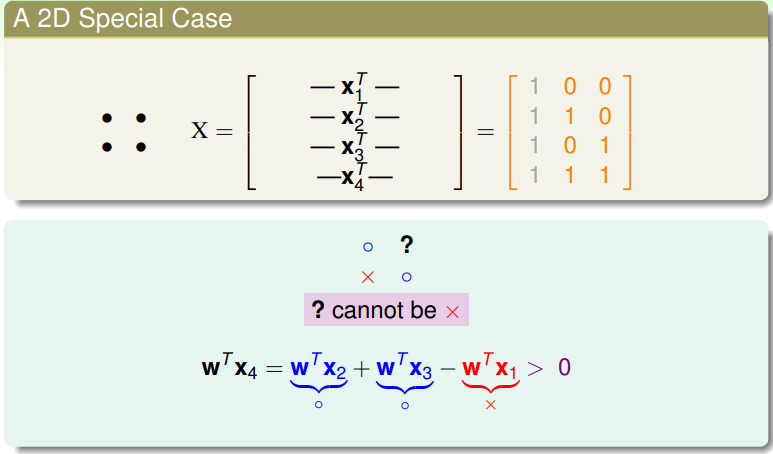 对于矩阵 ,代表了 4 个输入,其中第一列是 0 维数据,不必考虑;而第二列、第三列所表示的输入分别为 这三个之前可以 shatter 的点,若再增加一个点,则第四个点必然与前三者线性相关,即可以表示成 ,由此,若 ,那么 是必然的而不会存在 的可能,即不会存在 这种 dichotomy 的情形,这也就从代数上证明了 4个输入时无法shatter的原因 。即,线性相关性会限制可以产生 dichotomy 的数量。
对于矩阵 ,代表了 4 个输入,其中第一列是 0 维数据,不必考虑;而第二列、第三列所表示的输入分别为 这三个之前可以 shatter 的点,若再增加一个点,则第四个点必然与前三者线性相关,即可以表示成 ,由此,若 ,那么 是必然的而不会存在 的可能,即不会存在 这种 dichotomy 的情形,这也就从代数上证明了 4个输入时无法shatter的原因 。即,线性相关性会限制可以产生 dichotomy 的数量。 - 如果推广到一般性的 个长度的向量呢?
 个输入即行数为 ,但列数仍是 ,线性代数告诉我们这样的输入矩阵一定时线性相关的,由数学归纳,dichotomy 的数量必然是受限的,故 得证。
个输入即行数为 ,但列数仍是 ,线性代数告诉我们这样的输入矩阵一定时线性相关的,由数学归纳,dichotomy 的数量必然是受限的,故 得证。
- 同样的,这个命题要如何描述?
Physical Intuition of VC Dimension
上面的论证多少看着一头雾水,说了半天究竟什么是 VC Dimension?实际上,从物理地直觉来看,它代表了一种对自由度的估计:
- 一个假设被记作 ,其中 指的是为输入 中每个分量所对应的权重,能够调整的权重的数量 是这个假设的自由度;
- 而假设集的规模 是与自由度相关的数据,那么 代表着二分类问题的有效假设的自由度的大小: ,powerful 在这里的意思是该假设集对该问题的解释、包含的能力;
回想老问题:
- Positives Rays 中 ,可以调整的自由度为 1,即那个正负的分界点;
- Positive Intervals 中 ,即正负区间的分界点;

从此,我们可以用 代替之前对 M 的估计:
练习:直觉理解
- 这里权重 处要求必须保持为 0,那么自由度就是在 的基础上再 -1 ;
Interpreting VC Dimension
Penalty for Model Complexity
由前文论述可知,对任何 ,在足够大的取样 上,有
这个概率是 BAD events 发生的概率上界,换言之,GOOD events 发生的概率下界是
,因此我们可以得知
,从而,我们可以得到 的置信区间为:
,其中 称为模型的代价,即 penalty for model complexity。
VC Message
我们能从这个公式里得到什么信息?—— 一个非常全面、powerful 的 并不总是好的:
- 我们可以大概率地认为, ,将这个关系绘制成图:
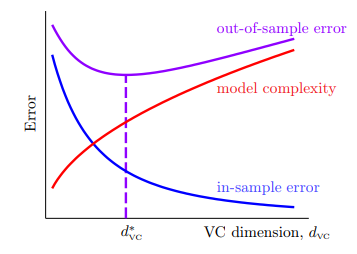
- 随着 的增加, 会降低,但是 会增加,从而 随之上升;
- 随着 的降低, 会降低,但是 会增加,从而 也会上升;
- 找到最佳的 是最能令人满意的,因此 不宜过大、也不宜过小;
因此,对于 ,如果给定 ,则对不同大小的输入样本数 N ,VC-bound 是这样:
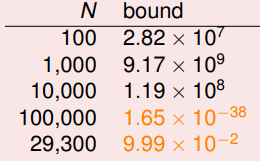
- 我们称之为样本复杂度(sample complexity),代表着样本数的规模,理论上 才够,但实际中发现 已经足够令人满意;
理论与实践的巨大差异,表明 VC bound 实际上非常宽松:
- 这是由于一方面,Hoeffding 不等式对 的估计本就非常宽松,
- 另一方面我们经过了一系列的取上界操作,如 等,进一步放宽了限制。
练习:如何降低获取 BAD data 的概率?

