70-complexity-analysis

封底估算

Cpp 一秒可以计算 $10^7\sim 10^8$ 次，因此只要最终时间复杂度在 $\mathcal{O}(10^7)$ 左右，就不会超时，但是常数过大时，也有可能超时。

根据数据大小反推算法

一般 ACM 或者笔试题的时间限制是 1 秒或 2 秒。在这种情况下，C++ 代码中的操作次数控制在 $10^7$ 为最佳。

下面给出在不同数据范围下，代码的时间复杂度和算法该如何选择：

1. $n\le 30$ 指数级别

• dfs + 剪枝：数字排列， n 皇后问题， 八数码问题，
• 状态压缩 dp：蒙德里安的梦想， 最短 Hamilton 路径

2. $n\le 100$ ⇒ $O(n^3)$

• floyd，
• dp，

3. $n\le 1000$ ⇒ $O(n^2)$ 、$O(n^2\log n)$

• dp，
• 二分，
• 朴素版 Dijkstra、朴素版 Prim、Bellman-Ford

4. $n\le 10000$ ⇒ $O(n\times \sqrt{n})$

• 块状链表、分块、莫队

5. $n\le 100000$ ⇒ $O(n\log n)$

各种 sort，线段树、树状数组、set/map、heap、dijkstra+heap、prim+heap、spfa、求凸包、求半平面交、二分

6. $n\le 1000000$ ⇒ $O(n)$ 、常数较小的 $O(n\log n)$

hash、双指针扫描、并查集，kmp、AC 自动机，

常数比较小的 $O(n\log n)$ 的做法：sort、树状数组、heap、dijkstra、spfa

7. $n\le 10000000$ ⇒ $O(n)$

双指针扫描、kmp、AC 自动机、线性筛素数

8. $n\le 10^9$ ⇒ $O(\sqrt{n})$

判断质数

9. $n\le 10^{18}$ ⇒ $O(\log n)$

最大公约数，快速幂

10. $n\le 10^{1000}$ ⇒ $O({\log }^{2}n)$

高精度加减乘除

11. $n\le 10^{100000}$ ⇒ $O(\log n\times \log \log n)$

高精度加减、FFT/NTT

算法时间复杂度分析实例

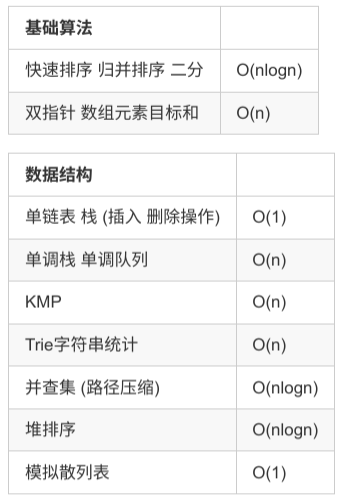
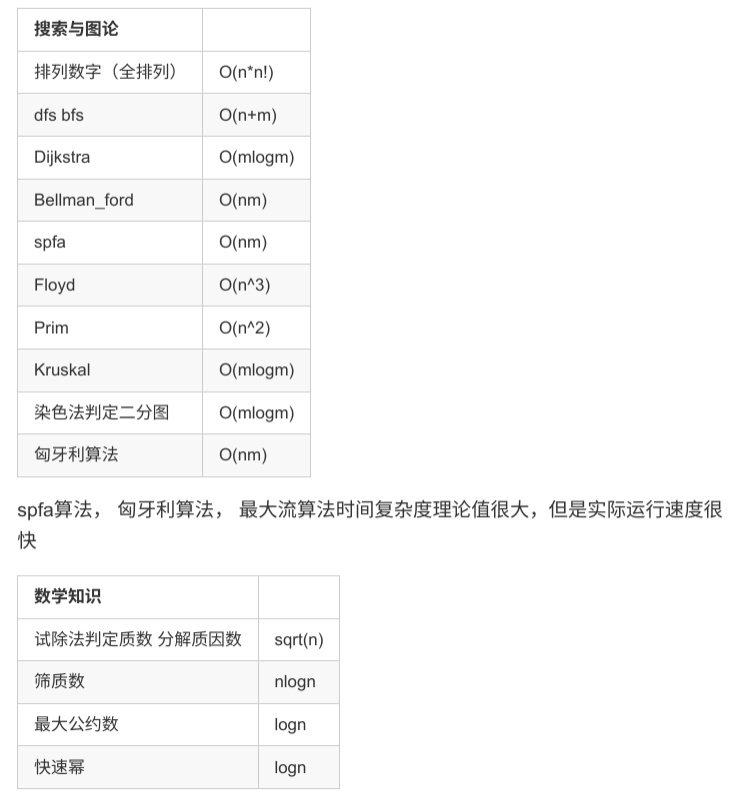
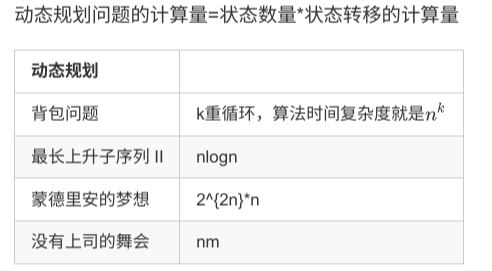
空间复杂度分析

64M

1 Byte = 8 bit

1 KB= 1024 Byte

1 MB=1024*1024 Byte

1 GB=1024 * 1024 * 1024 Byte

int  4 Byte

char 1 Byte

double, long long   6Byte

bool 1 Byte

64MB=2^26Byte

2^26Byte /4 =2^24 int

=1.6*10^7 int

注意 递归也是需要空间的，递归调用了系统栈，快速排序使用了递归，所以空间复杂度是 $O(\log n)$