快速排序
思路
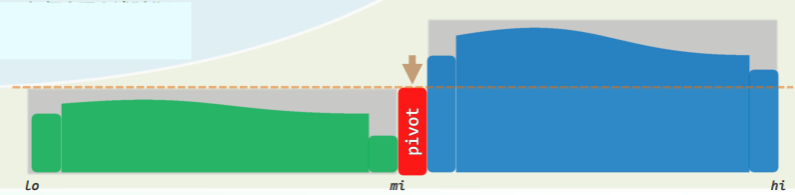
- 前缀、后缀各自(递归)排序之后,原序列便自然有序
- sorted (S) = sorted (SL) + pivot + sorted (SR)
- mergesort 难点在于合,而 quicksort 在于分
递归实现
template <typename T> //向量快速排序
void Vector<T>::quickSort( Rank lo, Rank hi ) { // 0 <= lo < hi <= size
if ( hi - lo < 2 ) return; //单元素区间自然有序,否则...
Rank mi = partition( lo, hi ); //在[lo, hi)内构造轴点
quickSort( lo, mi ); quickSort( mi + 1, hi ); //前缀、后缀各自递归排序
}
轴点选取
快速排序与轴点选取:
- 序列有序的必要条件: 轴点必定已然就位
- 特别地:在有序序列中,所有元素皆为轴点,反之亦然
- 快速排序:就是将所有元素逐个转换为轴点的过程
- 坏消息:在原始序列中,轴点未必存在
- derangement: 任何元素都不在原位
- 比如,顺序序列循环移位
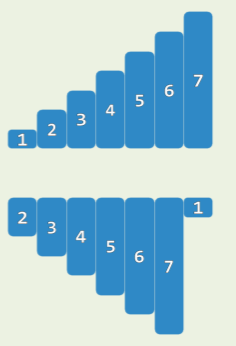
- derangement: 任何元素都不在原位
- 好消息:不需很多交换,即可使任一元素转为轴点
- 问题: 如何交换?成本多高?
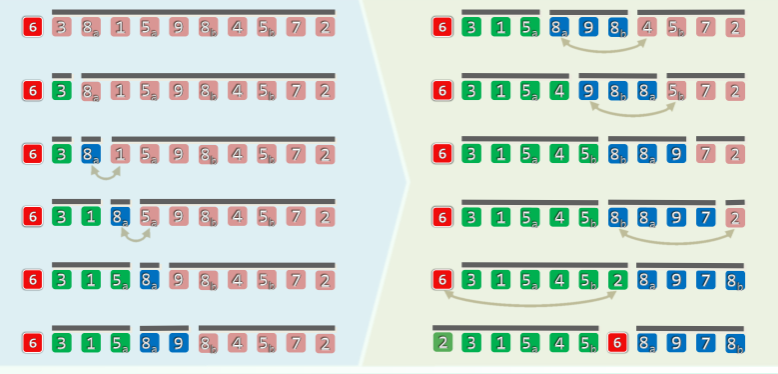
轴点划分:LUG 版
思路:减治
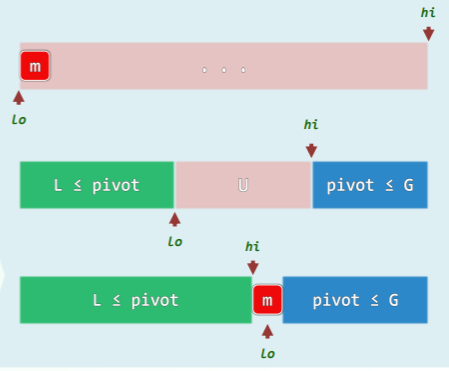
- 任取一个候选者(如
[0]) - 将序列划分为三段:L + U + G,分别是小于、未扫描到的、大于部分
- 交替地向内移动 lo 和 hi
- 逐个检查当前元素:
- 若更小/大,则转移归入 L/G
- 当 lo = hi 时,只需将候选者嵌入于 L、G 之间,即成轴点!
- 各元素最多移动一次(候选者两次) ——累计 O(n)时间、O(1)辅助空间
template <typename T> //通过调整元素位置,构造出区间[lo, hi)内的一个轴点
Rank Vector<T>::partition( Rank lo, Rank hi ) { // LUG版:基本形式
swap( _elem[lo], _elem[lo + rand() % ( hi - lo )] ); //任选一个元素与首元素交换
T pivot = _elem[lo]; //经以上交换,等效于随机选取候选轴点
while ( lo < hi ) { //从两端交替扫描,直至相遇
do hi--; while ( ( lo < hi ) && ( pivot <= _elem[hi] ) ); //向左拓展后缀G
if ( lo < hi ) _elem[lo] = _elem[hi]; //阻挡者归入前缀L,即凡小于轴点者,归入L部分
do lo++; while ( ( lo < hi ) && ( _elem[lo] <= pivot ) ); //向右拓展前缀L
if ( lo < hi ) _elem[hi] = _elem[lo]; //阻挡者归入后缀G,即凡大于轴点者,归入G
} // assert: quit with lo == hi or hi + 1
_elem[hi] = pivot; //候选轴点置于前缀、后缀之间,它便名副其实
return hi; //返回轴点的秩
}

L <= pivot <= G且U=[lo,hi)中,[lo]和[hi]交替空闲- 故序列中 U 部分单调减少,L 和 G 部分单调增加,这趟扫描一定能结束并正确归位 pivot
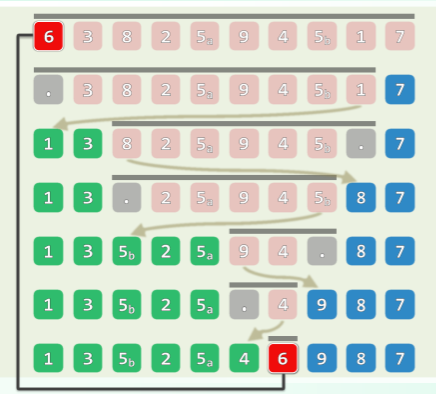 分析:
分析:
- 线性时间
- 尽管 lo 、hi 交替移动,但累计移动距离不过 O (n)
- in -place
- 只需 O (1)附加空间
- unstable
- lo/hi 的移动方向相反,左/右侧的大/小重复元素 可能前/后颠倒
轴点划分:DUP 版
思考多个雷同元素时,仍使用 LUG 策略的快速排序的情况:
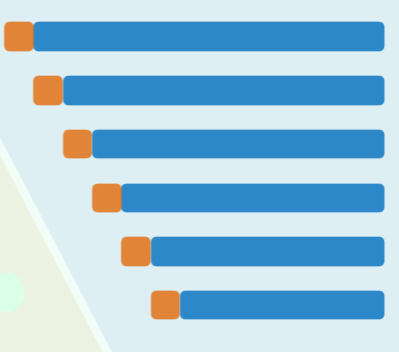
- 有大量元素与轴点雷同时,切分点将接近于 lo,划分极度失衡
- 更糟糕的是,这一最坏情况可能会持续发生,整个算法过程等效地退化为线性递归,
- 递归深度接近于 O (n) ,运行时间接近于 O (n^2)
- 直觉地改进,若移动 lo 和 hi 的过程中,同时比较相邻元素,若属于相邻的重复元素,则不再深入递归,但一般情况下,如此计算量反而增加,得不偿失
实际上,LUG 版略做调整,即可解决问题:
template <typename T> //通过调整元素位置,构造出区间[lo, hi)内的一个轴点
Rank Vector<T>::partition( Rank lo, Rank hi ) { // DUP版:可优化处理多个关键码雷同的退化情况
swap( _elem[lo], _elem[lo + rand() % ( hi - lo )] ); //任选一个元素与首元素交换
T pivot = _elem[lo]; //经以上交换,等效于随机选取候选轴点
while ( lo < hi ) { //从两端交替扫描,直至相遇
do hi--; while ( ( lo < hi ) && ( pivot < _elem[hi] ) ); //向左拓展后缀G,与LUG版相比,pivot的判断条件从<=变为<
if ( lo < hi ) _elem[lo] = _elem[hi]; //阻挡者归入前缀L,即凡不大于轴点者,归入L部分
do lo++; while ( ( lo < hi ) && ( _elem[lo] < pivot ) ); //向右拓展前缀L,同样这里由LUG版的<=变为<
if ( lo < hi ) _elem[hi] = _elem[lo]; //阻挡者归入后缀G,即凡不小于轴点者,归入G部分
} // assert: quit with lo == hi or hi + 1
_elem[hi] = pivot; //候选轴点置于前缀、后缀之间,它便名副其实
return hi; //返回轴点的秩
}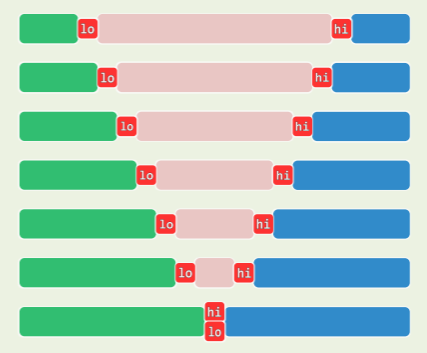
- 优点:
- 可以正确地处理一般情况和重复元素较多时情况,同时复杂度并未实质增高
- 遇到连续的重复元素时, lo 和 hi 会交替移动,切分点接近于 (lo+hi)/2
- 由 LUG 版的勤于拓展、懒于交换,转为懒于拓展、勤于交换
- 缺点:
- 交换操作有所增加, “更”不稳定
轴点划分:LGU 版
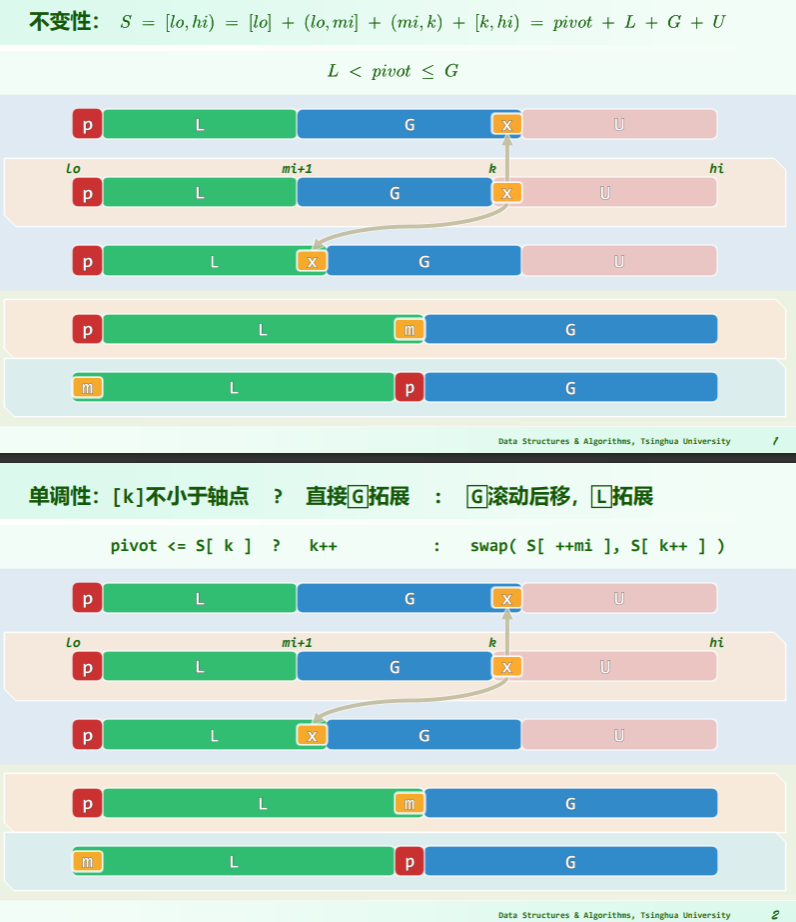
template <typename T> //轴点构造算法:通过调整元素位置构造区间[lo, hi)的轴点,并返回其秩
Rank Vector<T>::partition( Rank lo, Rank hi ) { // LGU版
swap( _elem[lo], _elem[lo + rand() % ( hi - lo )] ); //任选一个元素与首元素交换
T pivot = _elem[lo]; //以首元素为候选轴点――经以上交换,等效于随机选取
Rank mi = lo;
//++++++++++++++++++++++++++++++++++++++++++++++++++
//--- L<[lo] --- ] --- [lo]<=G --- ][ --- Unknown ---
//X x . . . . . x . . . . .. . . . x . . .. . . . x X
//| | | |
//lo mi k hi
//(lo is pivot candidate)+++++++++++++++++++++++++++
for ( Rank k = lo + 1; k < hi; k++ ) //自左向右扫描
if ( _elem[k] < pivot ) //若当前元素_elem[k]小于pivot,则
swap( _elem[++mi], _elem[k] ); //将_elem[k]交换至原mi之后,使L子序列向右扩展
//++++++++++++++++++++++++++++++++++++++++++++++++++++
//--- L<[lo] ---- ] ------------- [lo] <= G -----]
//X x . . . . . . x . . . . . . . . . . . . .. . x X
// | | |
// lo mi hi
// (lo is pivot candidate) +++++++++++++++++++++++++
swap( _elem[lo], _elem[mi] ); //候选轴点归位
return mi; //返回轴点的秩
}
迭代实现
思路
递归版快速排序的空间复杂度取决于递归深度,
- 最好情况:划分总是均衡的 //
O(logn) - 最坏情况:划分总是偏侧于一端 //
O(n) - 平均情况:均衡不致太少 //
O(logn)
如何避免最坏情况呢?
迭代版快速排序代码:
#define Put( K, s, t ) { if ( 1 < (t) - (s) ) { K.push(s); K.push(t); } }
#define Get( K, s, t ) { t = K.pop(); s = K.pop(); }
template <typename T> //向量快速排序
void Vector<T>::quickSort( Rank lo, Rank hi ) { //0 <= lo < hi <= size
Stack<Rank> Task; Put( Task, lo, hi );// 等效于对递归树的先序遍历
while ( !Task.empty() ) {
Get( Task, lo, hi );
Rank mi = partition( lo, hi ); //在[lo, hi)内构造轴点
if ( mi - lo < hi - mi ) { Put( Task, mi+1, hi ); Put( Task, lo, mi ); }
else { Put( Task, lo, mi ); Put( Task, mi+1, hi ); }
} //大任务优先入栈(小任务优先出栈执行),可保证递归深度(空间成本)不过O(logn)
}
性能分析
- 最好情况:每次划分都(接近)平均,轴点总是(接近)中央 —— 到达下界!
- 最坏情况:每次划分都极不均衡(比如,轴点总是最小/大元素) —— 与起泡排序相当!
- 采用随机选取(Randomization)、三者取中(Sampling)之类的策略只能降低最坏情况的概率,而无法杜绝
既如此,为何还称作快速排序?
分析递归深度

- 最坏情况(Ω(n) 递归深度),概率极低
- 平均情况(O (logn) 递归深度),概率极高
- 实际上:只要 pivot 并非过于侧偏,都会有效地缩短递归深度,因此不妨定义:
- 准居中:pivot 落在宽度为 的居中区间( λ 也是这种情况出现的概率)
- 则,每一递归路径上,至多出现 个准居中的 pivots
- 因此,每递归一层,都有 λ( 1-λ )的概率准居中(准偏侧)
- 深入 层后,可期望出现 次准居中,且有极高概率出现;
- 相反情况的概率则 < ,其随着 λ 的增加而下降,
- 比如 λ>1/3 后,即至少有 的概率,使得递归深度不超过
分析比较次数
递推分析

后向分析

k 选取
问题描述

- k 选取问题:在任意一组可比较大小的元素中,如何由小到大,找到次序为 k 者? 亦即,在这组元素的非降排序序列 S 中,找出
S[k]。 - 中位数选取:长度为 n 的有序序列 S 中,元素 称作中位数,在任意一组可比较大小的元素中,如何找到中位数?
- 中位数选取是一个 k 选取的特例,也是难度最大者
众数与中位数
无序向量中,若有一半以上元素同为 m,则称之为众数
- 在 {3,5,2,3,3} 中,众数为3;
- 在 {3,5,2,3,3,0} 中,却无众数
如何找到众数?
- 平凡算法:排序 + 扫描 //
O(nlogn+n) - 但进一步地,若限制时间不超过 O (n),附加空间不超过 O (1)呢?
- 必要性:众数若存在,则亦为必中位数
- 事实上:只要能够找出中位数,即不难验证它是否众数:
template <typename T>
bool majority( Vector<T> A, T & maj ){
return majEleCheck( A, maj = median( A ) ); // 验证是否为中位数
}
然而,在高效的中位数算法未知之前,如何确定众数的候选呢?——减治

- 若在向量 A 的前缀 P(|P|为偶数)中,元素 x 出现的次数恰占半数,则 A 有众数,仅当对应的后缀 A − P 有众数 m,且 m 就是 A 的众数
- 既然最终总要花费 O(n)时间做验证,故而只需考虑 A 的确含有众数的两种情况:
- 若 x = m,则在排除前缀 P 之后,m 与其它元素在数量上的差距保持不变
- 若 x != m,则在排除前缀 P 之后,m 与其它元素在数量上的差距不致缩小
- 若将众数的标准从“一半以上”改作“至少一半”,算法需做什么调整?—— 习题12-3
众数查找算法的实现:
template <typename T>
bool majority( Vector<T> A, T& maj ) { //众数查找算法:T可比较可判等
maj = majEleCandidate( A ); //必要性:选出候选者maj
return majEleCheck( A, maj ); //充分性:验证maj是否的确当选
}
template <typename T> T majEleCandidate( Vector<T> A ) { //选出具备必要条件的众数候选者
T maj; //众数候选者
// 线性扫描:借助计数器c,记录maj与其它元素的数量差额
for ( Rank c = 0, i = 0; i < A.size(); i++ )
if ( 0 == c ) { //每当c归零,都意味着此时的前缀P可以剪除
maj = A[i]; c = 1; //众数候选者改为新的当前元素
} else //否则
maj == A[i] ? c++ : c--; //相应地更新差额计数器
return maj; //至此,原向量的众数若存在,则只能是maj ―― 尽管反之不然
}
template <typename T> bool majEleCheck ( Vector<T> A, T maj ) { //验证候选者是否确为众数
Rank occurrence = 0; //maj在A[]中出现的次数
for ( Rank i = 0; i < A.size(); i++ ) //逐一遍历A[]的各个元素
if ( A[i] == maj ) occurrence++; //每遇到一次maj,均更新计数器
return 2 * occurrence > A.size(); //根据最终的计数值,即可判断是否的确当选
}
中位数选取
归并向量的中位数如何找到?任给有序向量 和 ,长度为 和 ,如何快速找出 的中位数:

- 蛮力:经归并得到有序向量 S,取 即是;
- 如此共需 时间,但未能利用两个向量的有序性;
- 减治思路:
- 考查 和

- 若 ,则它们同为 的中位数
- 若 ,则无论 n 为奇偶,必有 ,这意味着,如此减除(一半规模)之后,中位数不变
- 若 同理;
- 故经上思路不断剪枝,可以得到
O(log(min(n1,n2)))时间内找到中位数的算法:
//等长子向量
template <typename T> // S1[lo1, lo1 + n)和S2[lo2, lo2 + n)分别有序,n > 0,数据项可能重复
T median( Vector<T>& S1, Rank lo1, Vector<T>& S2, Rank lo2, Rank n ) { //中位数算法(高效版)
if ( n < 3 ) return trivialMedian( S1, lo1, n, S2, lo2, n ); //递归基
Rank mi1 = lo1 + n / 2, mi2 = lo2 + ( n - 1 ) / 2; //长度(接近)减半
if ( S1[mi1] < S2[mi2] )
return median ( S1, mi1, S2, lo2, n + lo1 - mi1 ); //取S1右半、S2左半
else if ( S1[mi1] > S2[mi2] )
return median ( S1, lo1, S2, mi2, n + lo2 - mi2 ); //取S1左半、S2右半
else
return S1[mi1];
}
// 中位数算法蛮力版:效率低,仅适用于max(n1, n2)较小的情况
template <typename T> //子向量S1[lo1, lo1 + n1)和S2[lo2, lo2 + n2)分别有序,数据项可能重复
T trivialMedian( Vector<T>& S1, Rank lo1, Rank n1, Vector<T>& S2, Rank lo2, Rank n2 ) {
Rank hi1 = lo1 + n1, hi2 = lo2 + n2;
Vector<T> S; //将两个有序子向量归并为一个有序向量
while ( ( lo1 < hi1 ) && ( lo2 < hi2 ) )
S.insert( S1[lo1] <= S2[lo2] ? S1[lo1++] : S2[lo2++] );
while ( lo1 < hi1 ) S.insert( S1[lo1++] );
while ( lo2 < hi2 ) S.insert( S2[lo2++] );
return S[( n1 + n2 ) / 2]; //直接返回归并向量的中位数
}
//任意长度的子向量
template <typename T> //向量S1[lo1, lo1 + n1)和S2[lo2, lo2 + n2)分别有序,数据项可能重复
T median ( Vector<T>& S1, Rank lo1, Rank n1, Vector<T>& S2, Rank lo2, Rank n2 ) { //中位数算法
if ( n1 > n2 ) return median( S2, lo2, n2, S1, lo1, n1 ); //确保n1 <= n2
if ( n2 < 6 ) //递归基:1 <= n1 <= n2 <= 5
return trivialMedian( S1, lo1, n1, S2, lo2, n2 );
//////////////////////////////////////////////////
// lo1 lo1 + n1/2 lo1 + n1 - 1
// | | |
// X >>>>> X >>>>>>>>> X
// Y .. trimmed .. Y >>>>> Y >>>>>>>>> Y .. trimmed .. Y
// | | | | |
// lo2 lo2+(n2-n1)/2 lo2+n2/2 lo2+(n2+n1)/2 lo2+n2-1
//////////////////////////////////////////////////
if ( 2 * n1 < n2 ) //若两个向量的长度相差悬殊,则长者(S2)的两翼可直接截除
return median( S1, lo1, n1, S2, lo2 + ( n2 - n1 - 1 ) / 2, n1 + 2 - ( n2 - n1 ) % 2 );
//////////////////////////////////////////////////
// lo1 lo1 + n1/2 lo1 + n1 - 1
// | | |
// X >>>>>>>>>>>>>>> X >>>>>>>>>>>>>>>>>>>>> X
// |
// m1
//////////////////////////////////////////////////
// mi2b
// |
// lo2 + n2 - 1 lo2 + n2 - 1 - n1/2
// | |
// Y <<<<<<<<<<<<<<< Y ...
// .
// .
// .
// .
// .
// .
// .
// ... Y <<<<<<<<<<<<<<< Y
// | |
// lo2 + (n1-1)/2 lo2
// |
// mi2a
///////////////////////////////////////////////////
Rank mi1 = lo1 + n1 / 2;
Rank mi2a = lo2 + ( n1 - 1 ) / 2;
Rank mi2b = lo2 + n2 - 1 - n1 / 2;
if ( S1[mi1] > S2[mi2b] ) //取S1左半、S2右半
return median( S1, lo1, n1 / 2 + 1, S2, mi2a, n2 - ( n1 - 1 ) / 2 );
else if ( S1[mi1] < S2[mi2a] ) //取S1右半、S2左半
return median( S1, mi1, ( n1 + 1 ) / 2, S2, lo2, n2 - n1 / 2 );
else //S1保留,S2左右同时缩短
return median( S1, lo1, n1, S2, mi2a, n2 - ( n1 - 1 ) / 2 * 2 );
} //O(log(min(n1,n2))) ,可见实际上等长版本才是难度最大的
快速选取
蛮力法:排序
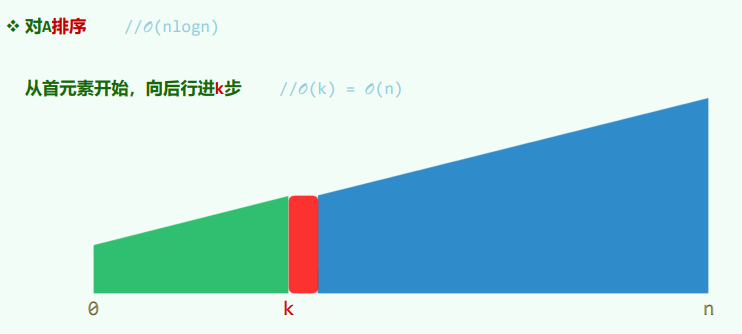
建堆法
-
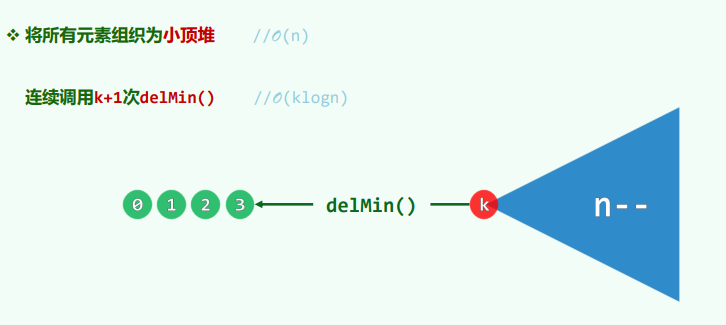
建立小顶堆:
-
建立大顶堆:
- 任选 k+1 个元素(
A[0,k]内的元素),组织为大顶堆 //O(k) - 对剩余元素,依次插入堆中,再从堆中删除最大值 // `(n-k)*O(logk)*O(logk)=O(2(n-k)logk)
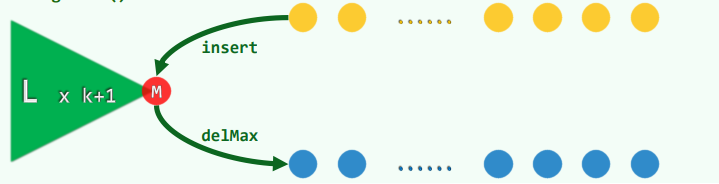
- 任选 k+1 个元素(
-
建立两个堆
- 将输入向量任意划分为规模 k 、n-k 的子集,分别组织大、小顶堆 //
O(k+(n-k))=O(n) - 当大顶堆的顶小于小顶堆的顶时,交换之并分别下滤 //
O(logk), O(log(n-k)) - 重复直到大顶堆的顶 > 小顶堆的顶,返回小顶堆即可;

- 将输入向量任意划分为规模 k 、n-k 的子集,分别组织大、小顶堆 //
快速选取法
所谓第 k 小,是相对于序列整体而言,所以在访问每个元素至少一次之前,绝无可能确定,因此快速选取的下界是Ω(n)——最快也不过如此。
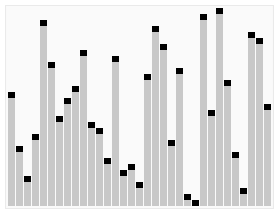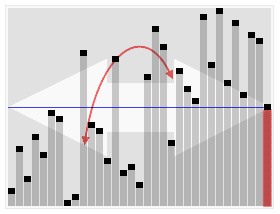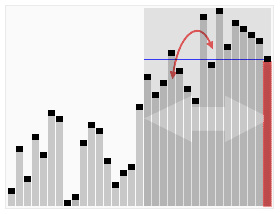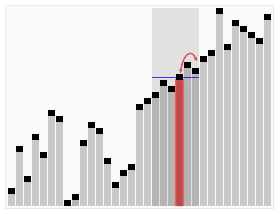
template <typename T> void quickSelect( Vector<T>& A, Rank k ) { //基于快速划分的k选取算法
for ( Rank lo = 0, hi = A.size(); lo < hi; ) {
Rank i = lo, j = hi; T pivot = A[lo]; //大胆猜测
while ( i < j ) { //小心求证:O(hi - lo + 1) = O(n)
do j--; while ( ( i < j ) && ( pivot <= A[j] ) );
if ( i < j ) A[i] = A[j];
do i++; while ( ( i < j ) && ( A[i] <= pivot ) );
if ( i < j ) A[j] = A[i];
} // assert: quit with i == j or j+1
A[j] = pivot; // A[0,j) <= A[j] <= A(j, n)
if ( k <= j ) hi = j; //suffix trimmed (剪枝后缀)
if ( i <= k ) lo = i; //prefix trimmed
} //A[k] is now a pivot
}
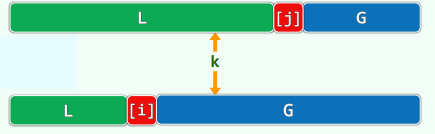
- 记期望的比较次数为 ,有
- 可以证明
- 不难验证
线性选取
LinearSelect(A,n,k):从长度为 n 的向量 A 中,选取第 k 大的元素:
0. 设定 Q 作为较小的常数(如 2),判断如果向量 A 的长度 n 小于 Q,则用遍历的方法直接给出其中的第 k 大元素;
- 若 A 的长度大于 Q,则将 A 均匀地分成 n/Q 个子向量,每个子向量的长度为 Q,
- 对每个子向量排序并找出其中的中位数——得到 n/Q 个中位数;
- 递归地调用
LinearSelect()寻找 n/Q 个中位数的中位数,记作 M ; - 将 A 划分为三个区段,分别是 L 段(
x<M),E 段(x=M),G 段(x>M); - 如果所要选取的第 k 大元素,
- if
k <= |L|即该元素在 L 段,则返回LinearSelect(A,k), - elif
k <= |L+E|即该元素在 L 或 E 段,则返回 M; - else
k <= |L+E+G|即该元素在 G 段,返回LinearSelect(G,k - |L| - |E|)
- if
- 上述都是递归地进行。
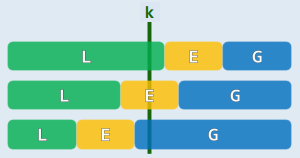
复杂度分析:将 linearSelect()算法的运行时间记作 T(n)
- 第 0 步:O (1) = O (QlogQ) //递归基:序列长度|A| ⇐ Q
- 第 1 步:O (n) //子序列划分
- 第 2 步:O (n) = Q^2 * n/Q //子序列各自排序,并找到中位数
- 第 3 步:T (n/Q) //从 n/Q 个中位数中,递归地找到全局中位数
- 第 4 步:O (n) //划分子集 L/E/G,并分别计数 —— 一趟扫描足矣
- 第 5 步:T(3n/4)
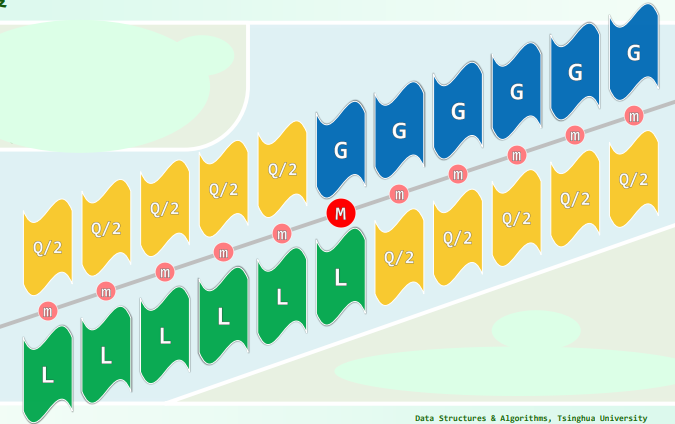
希尔排序
思路
ShellSort:将整个序列视作一个矩阵,逐列各自排序

- 递减增量策略:
- 由粗到细:重排矩阵,使其更窄,再逐列排序
- 逐步求精,如此往复,直至矩阵变成一列
- 步长序列 step sequence:由矩阵宽度升序排列而成的序列
- 正确性:最后一次迭代等同于全排序:
h-sorting -> 1-sorting,实际操作是插入排序; - 可见,相较于归并排序是在向量横向上分块,而希尔排序是在向量纵向上分块。
实例
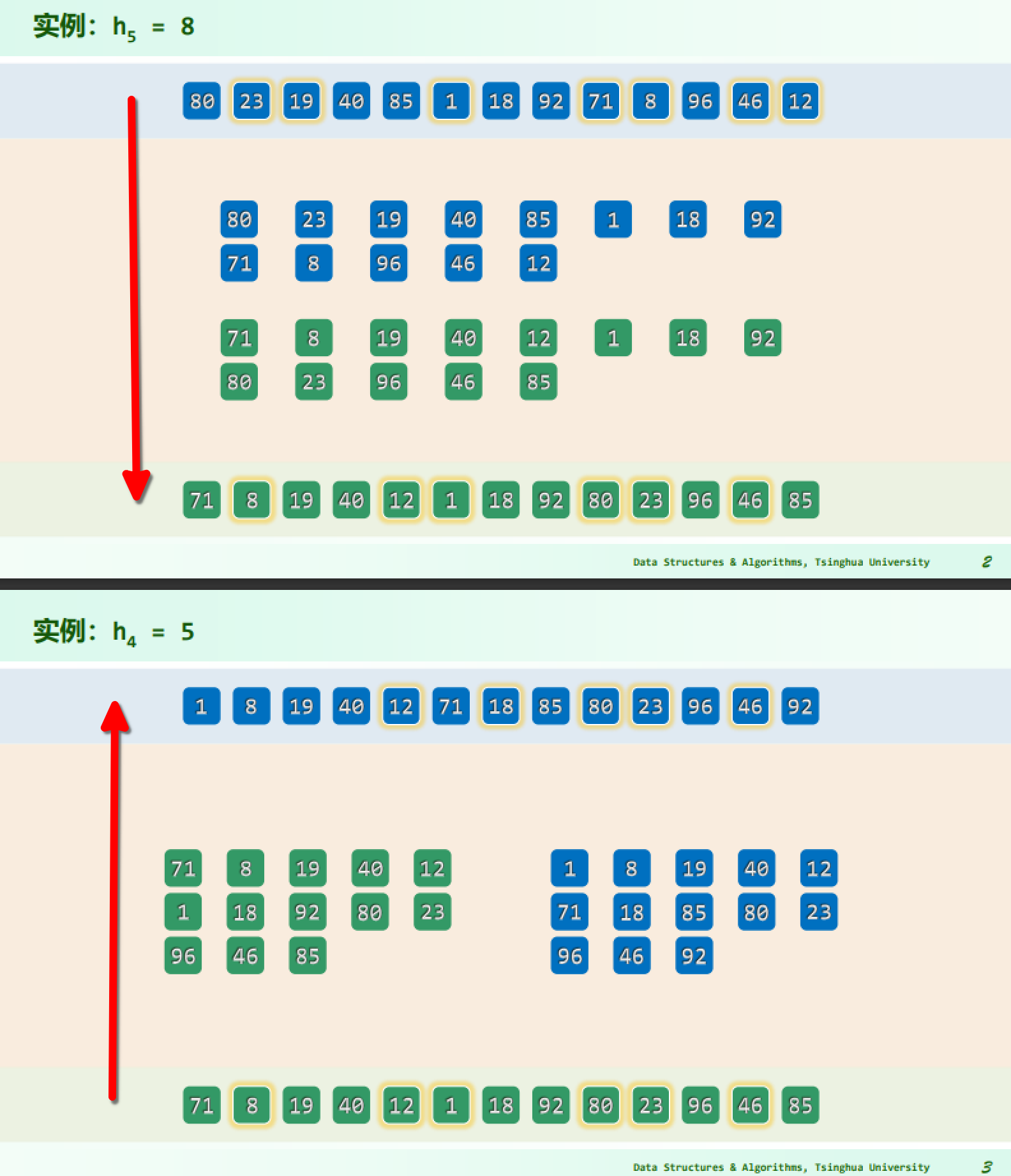
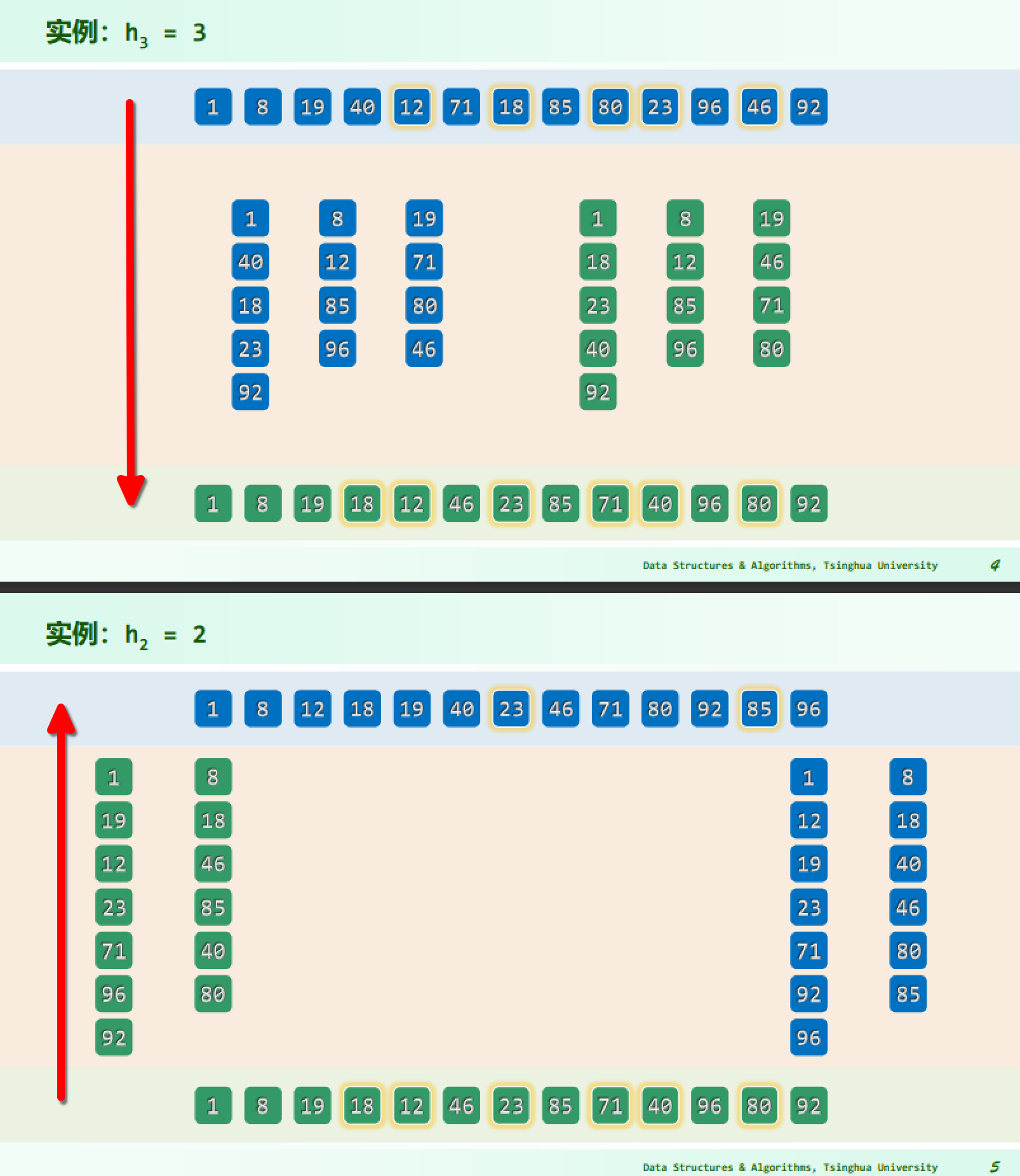
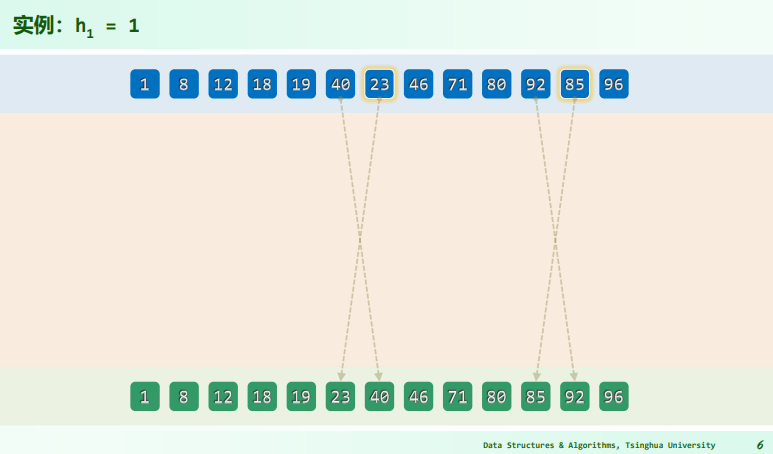
实现
如何实现矩阵重排?借助一维向量足矣:
- 每步迭代中,若当前矩阵宽度为 h,则
B[i][j] = A[i*h+j] 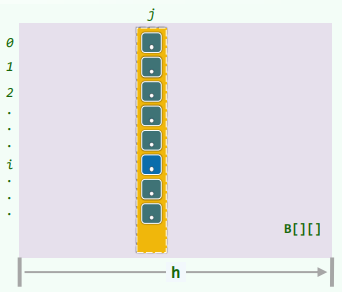
- 或
A[k] = B[k/h][k%h] 
template <typename T> //向量希尔排序
void Vector<T>::shellSort( Rank lo, Rank hi ) {
for ( Rank d = 0x7FFFFFFF; 0 < d; d >>= 1 ) // PS Sequence: { 1, 3, 7, 15, 31, ... }
for ( Rank j = lo + d; j < hi; j++ ) { // for each j in [lo+d, hi)
T x = _elem[j]; Rank i = j; // within the prefix of the subsequence of [j]
while ( ( lo + d <= i ) && ( x < _elem[i - d] ) ) // find the appropriate
_elem[i] = _elem[i - d], i -= d; // predecessor [i]
_elem[i] = x; // where to insert [j]
}
}// 0 <= lo < hi <= size <= 2^31
输入敏感性与希尔排序性能分析
shell 序列
当步长序列(每次运行时矩阵的宽度)为 时,最坏情况下需要 的时间。
- 考查由子序列 和 交错而成的序列:

- 在倒数第二趟——
2-sorting时,A、B 各成一列进行矩阵重排,得到的结果如下: 
- 然而此时逆序对仍然很多,最后一趟
1-sorting需要 的时间 - 这一现象的原因在于 中的各项并不互素,相邻项也不互素。
邮资问题
考查如下问题: 假设在某个国家,邮局仅发行面值分别为4分和13分的两种邮票,那么
- 准备邮寄平信的你,可否用这两种邮票组合出对应的 50 分邮资?
- 准备邮寄明信片的你,可否用这两种邮票组合出对应的35 分邮资?
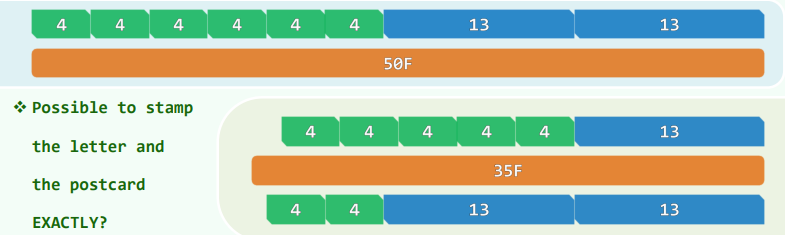
由上可见,邮资 P 一定属于集合
线性组合
用数论的语言,邮资问题即是 4n+13m=35 是否存在 n、m 都为非负整数的解?
对任意自然数 g 和 h,只要 n 和 m 也是自然数,
- 则称 为 g 和 h 的一个线性组合,
- 称 为不能由 g 和 h 线性组合的数字
- 将不能由 g 和 h 组合生成出来的最大自然数记作
x(g,h),即
数论的基本结论:如果 g 和 h 互素,则必有 ,即 x(4,13)=35 。
h-soring 和 h-sorted
在向量 S[0,n) 中,若 S[i]<=S[i+h] 对任何 0<=i<n-h 均成立,则称该向量 h-sorted,将向量由 h-unsorted 进行排序操作得到 h-sorted 状态的过程,称作 h-sorting:
- 可见,1-sorted 状态是全局向量有序的;
- Knuth 给出了一个重要结论:已经 g-sorted 的向量,再经一次 h-sorting,必然仍保持 g-sorted,此时对 h 和 g 都有序,记作 (g, h)-sorted.
-有序序列必然(mg+nh)-有序.png)
- 上图表示 (g, h)-sorted 的向量必然 (mg+nh)-sorted
有序性的保持和加强
根据 Knuth 指出的性质,随着 h 的不断递减,h-sorted 向量整体的有序性必然逐渐改善。
考查与任一元素 S[i] 构成逆序对的后继元素(这里要回顾一下 习题 3-11 的知识):

- 在分别做过 g-排序与 h-排序之后,根据 Knuth 的结论可知该向量必已 (g, h)-有序。由以上分析,对于 g 和 h 的任一线性组合 mg + nh,该向量也应 (mg + nh)-有序。因此反过来,逆序对的间距必不可能是 g 和 h 的组合。而根据此前所引数论中的结论,只要 g 和 h 互素,则如图所示,逆序对的间距就绝不可能大于 (g - 1)∙(h - 1)。
- 由此可见,希尔排序过程中向量的有序性之所以会不断积累并改善,其原因可解释为,向量中每个元素所能参与构成的逆序对持续减少,整个向量所含逆序对的总数也持续减少。与此同时,随着逆序对的减少,底层所采用的插入排序算法的实际执行时间,也将不断减少,从而提高希尔排序的整体效率。
(g, h)-sorted 时 d-sorting 的排序成本
设某向量 S 已属(g, h)-sorted,且假设 g 和 h 的数值均处于 O(d) 数量级,以下考查对该向量做 d-sorting 所需的时间成本:
- 据其定义,d-sorting 需将 S 等间距地划分为长度各为
O(n/d)的 d 个子向量,并分别排序。 - 由以上分析,在 (g, h)-sorted 的向量中,逆序对的间距不超过 (g - 1)∙(h - 1) 故就任何一个子向量的内部而言,逆序对的间距应不超过 (g - 1)∙(h - 1) / d =
O(d) - 再次根据 习题 3-11 的结论,采用插入排序算法可在:
O(d)∙(n/d)=O(n)的时间内,完成每一子向量的排序; - 于是,所有子向量的排序总体消耗的时间应不超过
O(dn)。
特殊步长序列
Papernov-Stasevic Seq
回到增量序列的优化设计问题。按照此前“尽力避免增量值之间公共因子”的思路,Papernov 和 Stasevic 于1965年提出了另一增量序列:
不难看出,其中相邻各项的确互素。采用这一增量序列,希尔排序算法的性能可以改进至 ,其中 n 为待排序向量的规模。
在序列 的各项中,设 为与 最接近者,亦即 。以下将希尔排序算法过程中的所有迭代分为两类,分别估计其运行时间。
- 首先,考查在 之前执行的各步迭代。这类迭代所对应的增量均满足 ,或等价地,k > t。在每一次这类迭代中,矩阵共有 列,各列包含 个元素。因此,若采用插入排序算法,各列分别耗时 ,所有列共计耗时 。于是,此类迭代各自所需的时间 构成一个大致以 2 为比例的几何级数,其总和应线性正比于其中最大的一项,亦即不超过
- 对称地,再来考查 之后的各步迭代。 这类迭代所对应的增量均满足 ,或等价地,k < t。考虑到此前刚刚完成 -sorting 和 -sorting,而来自 序列的 和 必然互素,且与 同处一个数量级。因此根据此前结论,每一次这样的迭代至多需要 时间。同样地,这类迭代所需的时间 也构成一个大致以 2 为比例的几何级数,其总和也应线性正比于其中最大的一项,亦即不超过
综上可知,采用 序列的希尔排序算法,在最坏情况下的运行时间不超过 。(注意到外循环会发生 次)

Pratt Seq
Pratt 于1971年也提出了自己的增量序列:
可见,其中各项除2和3外均不含其它素因子,并且其中项数为 ,且都不大于 n 。
可以证明,采用 序列,希尔排序算法至多运行 时间(习题12-14)。
Sedgewick Seq
尽管 Pratt 序列的效率较高,但因其中各项的间距太小,会导致迭代趟数过多,此时对已经基本有序的序列耗时较久。为此, Sedgewick 综合 Papernov-Stasevic 序列与 Pratt 序列的优点,提出了以下增量序列: 其中各项,均为: 或 的形式。
如此改进之后,希尔排序算法在最坏情况下的时间复杂度为 ,平均复杂度为 。 更重要的是,在通常的应用环境中,这一增量序列的综合效率最佳。
[! problem] 存在使希尔排序复杂度为
O(nlogn)的步长序列吗? PS 序列在 70 的量级后, Sedgewick 序列在 的量级后,由前文证明,基于 CBA 式的排序算法下界为 ,希尔排序的步长序列应能进一步优化。
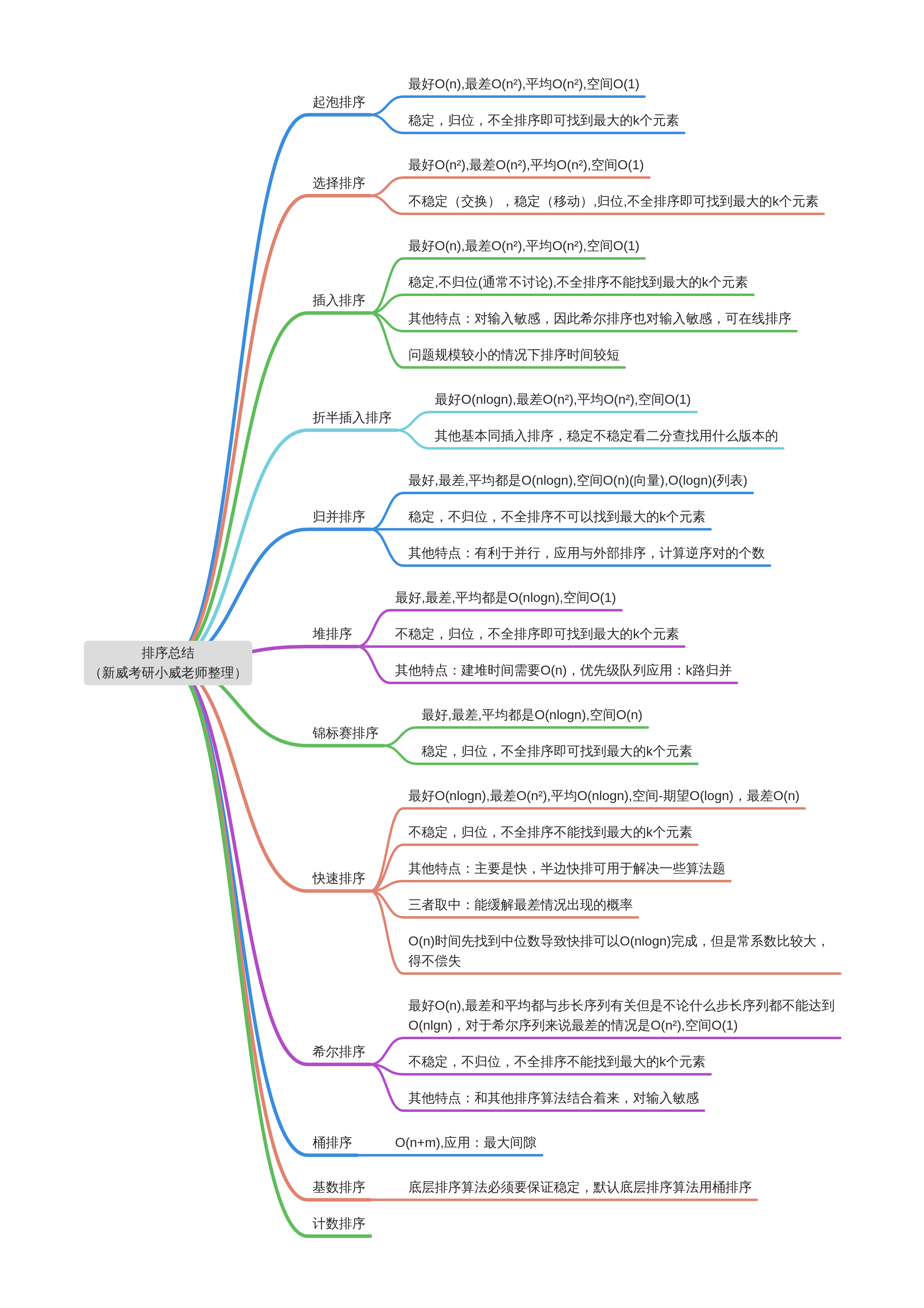
排序大总结