F0-Validation

Model Selection Problem

迄今为止我们学习了 ML 中许多概念，他们分属 ML 流程的各个阶段，诸如学习算法 $\mathcal{A}$ 、迭代轮次 $T$ 、迭代步长 $\eta$ 、转换函数 $\Phi$ 、正则化方法 $\Omega (\mathbf{w})$ 、正则限制 $\lambda$ ：

• 
• 这些方法的构成了大量的组合，从中如何选取应对目标问题最合适的方法组合呢？

选取最佳模型的问题可以更加规范的叙述如下：

• 
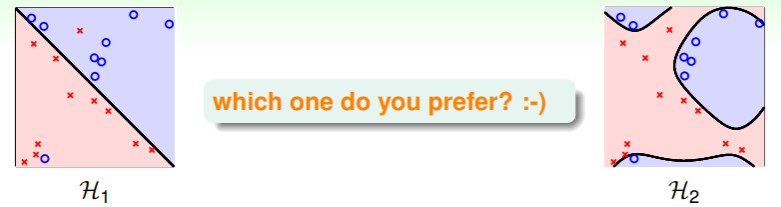
• 给定 M 个模型，它们分别来自假设集 ${\mathcal{H}}_1,{\mathcal{H}}_2,{\mathcal{H}}_3,...,{\mathcal{H}}_M$ ，并通过 ${\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,...,{\mathcal{A}}_M$ 学习得来；
• 我们的目标是在某个假设集 ${\mathcal{H}}_{m^{\ast }}$ 中选取特定的假设 $g_{m^{\ast }}={\mathcal{A}}_{m^{\ast }}(\mathcal{D})$ ，其能够获得较低的 $E_{out}$ ，
• 然而问题是我们并不知道具体的分布 $P(\mathbf{x})\&P(y|\mathbf{x})$ ，当然也就无从得知 $E_{out}$ ——这是 ML 中最关键的实操性问题。

Why not Best $E_{in}$ ?

我们可以从所有假设中选取使得 $E_{in}$ 最小者吗？即 $m^{\ast }=arg\underset{1\le m\le M}{\min }(E_m=E_{in}({\mathcal{A}}_m(\mathcal{D}))$ ？

当然不行，具体有以下几个原因：

1. 我们之前谈论过，高维假设集中获得的假设在 $E_{in}$ 上的表现通常优于低维假设集中的；同样，没有限制（即 $\lambda =0$）的表现也通常优于有限制时。但是这两种情况都有较大可能导致过拟合问题的发生；
2. 另外，如果算法 ${\mathcal{A}}_1$ 在假设集 ${\mathcal{H}}_1$ 中获得最小的 $E_{in}$ ，而算法 ${\mathcal{A}}_2$ 在假设集 ${\mathcal{H}}_2$ 中获得最小的 $E_{in}$ ，那么要找到 $g_{m^{\ast }}$ ，就要在两个假设集 ${\mathcal{H}}_1\cup {\mathcal{H}}_2$ 中选取，这时 VC dimension 将达到 $d_{VC}({\mathcal{H}}_1\cup {\mathcal{H}}_2)$ ，因此复杂度很大，不利于推广；

因此选取最小的 $E_{in}$ 是危险的、不可靠的。

Why not a Fresh ${\mathcal{D}}_{test}$ ?

我们可以在一个新的数据集 ${\mathcal{D}}_{test}$ 上进行评估，选取使得最小的 $E_{test}$ 的假设吗？即 $m^{\ast }=arg\underset{1\le m\le M}{\min }(E_m=E_{test}({\mathcal{A}}_m(\mathcal{D}))$ ？

尽管 Hoeffding 不等式可以确保这种推广是可信的：

$$E_{out}(g_{m^{\ast }})\le E_{test}(g_{m^{\ast }})+O\left(\sqrt{\frac{\log M}{N_{test}}}\right)$$

，但是 ${\mathcal{D}}_{test}$ 从何而来？难道拿着真题检验做题能力吗？这不过是自欺欺人罢了。

Combination of $E_{in}$ and $E_{test}$

不过，我们比较、总结 $E_{in}$ 和 $E_{test}$ 这两种方式：

• 
• 我们似乎可以结合二者的特点，推导出一种新的评估方式：计算数据集来自手头拥有的训练集 $\mathcal{D}$ ，并且从中取出不被任何学习算法使用过的一小部分：${\mathcal{D}}_{val}$ ——自欺欺人，但是在自己的数据上（就像把手头的题区分成模拟题和往年真题😀）

练习：理解最佳假设

Validation

我们最初的思路就是从原来规模为 N 的数据集 $\mathcal{D}$ 中通过学习算法 ${\mathcal{A}}_m$ 学习到最佳估计 $g_m$ ，其能够满足最小的 $E_{in}$ 。现在，引入 validation 后，我们将数据集一分为二，其中一份是用于验证的规模为 K 的验证集 ${\mathcal{D}}_{val}$ ，另一份是规模为 $N-K$ 的训练集 ${\mathcal{D}}_{train}$ ：

• 
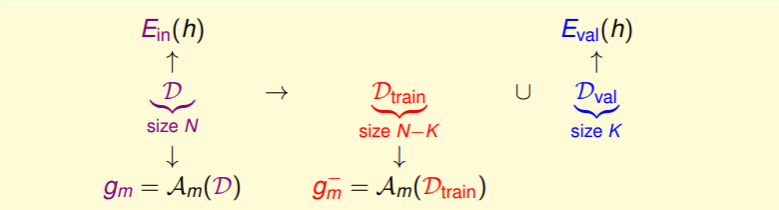
• 为了使 $E_{val}$ 和 $E_{out}$ 能够联系起来，我们需要验证集 ${\mathcal{D}}_{val}\stackrel{\text{i.i.d}}{\sim }P(\mathbf{x},y)$ ，即是从数据集 $\mathcal{D}$ 中随机地、均匀地、独立地抽取；
• 为了保证 ${\mathcal{D}}_{val}$ 是“干净”的，我们要求学习算法 ${\mathcal{A}}_m$ 只能在训练集 ${\mathcal{D}}_{train}$ 上训练；（就像做题时先做模拟题，最后在往年真题上再加测试评估）

由 Hoeffding 不等式可以保证，$E_{out}$ 与 $E_{val}$ 有如下关系：

$$E_{out}(g_m^{-})\le E_{val}(g_m^{-})+O\left(\sqrt{\frac{\log M}{K}}\right)$$

因此我们在选取合适的假设时，应当是从训练集上完成训练的模型里，通过验证集逐一验证，取错误率最低者为 selected model ：

• 
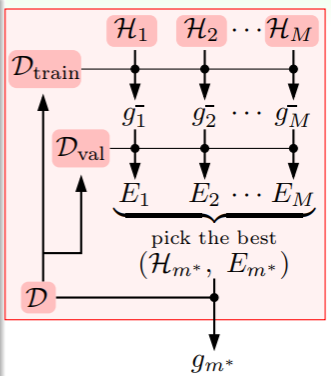
• 选取方法用数学语言描述即是：$m^{\ast }=arg\underset{1\le m\le M}{\min }(E_m=E_{val}({\mathcal{A}}_m({\mathcal{D}}_{train})))$
• 不过上图中有一点需要注意，就是在选择错误率最低的假设后，仅是得到了 $g^{-}$ ，还要在 ${\mathcal{D}}_{train}\cup {\mathcal{D}}_{val}$ 上再次训练一遍，最后才能得到 $g_{m^{\ast }}$ ；
• 因此完整的概率关系为：$E_{out}(g_{m^{\ast }})\le E_{out}(g_{m^{\ast }}^{-})\le E_{val}(g_{m^{\ast }}^{-})+O\left(\sqrt{\frac{\log M}{K}}\right)$

我们在两种假设集 ${\mathcal{H}}_{{\Phi }_5}$ 和 ${\mathcal{H}}_{{\Phi }_{10}}$ 上做选择，看看验证集大小对 $E_{out}$ 的影响：

• 
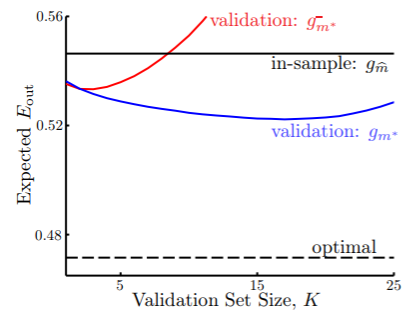
• 这里 in-sample 的假设 $g_{\hat{m}}$ 是用整个数据集 $\mathcal{D}$ 得到的，而 optimal 是理想的验证集（考试真题），因此它是不可获得的、但效果最好的；
• $g_{m^{\ast }}^{-}$ 是只经过训练集验证就选取的假设，它之所以会在验证集大小到一定规模时急剧上升，是因为训练集过小，导致拟合程度不足；
• $g_{m^{\ast }}$ 是经过训练集验证后选取的最佳假设集 ${\mathcal{H}}_{m^{\ast }}$，之后在完整的数据集 $\mathcal{D}$ 上训练得到，充分参考了训练集和验证集，因此它的效果是可以做到的最好的；
• 这里在验证集规模 $K$ 上出现了一个窘境：
  • 大的 $K$ 可以认为 $E_{out}(g^{-})\approx E_{val}(g^{-})$ ，但是训练集不足导致的欠拟合影响颇大，
  • 而小的 $K$ 可以认为 $E_{out}(g)\approx E_{out}(g^{-})$ ，但是验证集不足导致 $E_{val}$ 的意义不够明显，过拟合的风险增加，
  • 因此选取合适的 $K$ 值至关重要，在实践中 $K=\frac{N}{5}$ 一般认为是合适的比例；

练习：理解正确的验证流程

• 注意如果使用 $\mathcal{D}$ 直接获取 $E_{in}$ ，则需要 $25N^2$ 的时间，这说明验证并不意味着要花费更多时间；

Leave-One-Out Cross Validation

不过，除了选择 $K=\frac{N}{5}$ 这样的比例，我们尝试使用 $K=1$ 这样的极端情况：

• 此时由于只挑选了一个样本用于验证，因此可以认为 $E_{out}(g)\approx E_{out}(g^{-})$ ，
• 具体地，我们挑选数据集中第 $n$ 个样本作为训练集： ${\mathcal{D}}_{val}^{(n)}=({\mathbf{x}}_n,y_n)$ ，此时进行验证的错误评估为 $E_{val}^{(n)}(g_n^{-})=\text{err}(g_n^{-}({\mathbf{x}}_n,y_n)\stackrel{\text{denoted as}}{⟹}{e}_n$ ，

但是由于验证集太小，$E_{out}(g^{-})$ 与 $E_{val}(g^{-})$ 的关系极其薄弱、差距极大，并且只有 1 个样本的验证集只能告诉我们正确与否，而不能得到正确的可信概率，因此我们需要重复这样的流程：

• 抽出一个样本作为验证集，训练后在该验证集上验证，获得结果；接着再次重新随机抽取一个样本作为验证集，重新训练再次验证… 最后，对多次验证的结果进行错误评估，这样就得到了足够多的 $e_n$ 以靠近 $E_{out}(g)$ ，
• 上面的流程就称作 Leave-One-Out Cross Validation ，其错误评估函数为 $E_{loocv}(\mathcal{H},\mathcal{A})=\frac{1}{N}\sum _{n=1}^N{e}_n=\frac{1}{N}\sum _{n=1}^N\text{err}(g_n^{-}({\mathbf{x}}_n),y_n)$

以一个简单的图例说明留一交叉验证法的使用方法：

• 在三个样本中通过线性回归拟合一条直线：
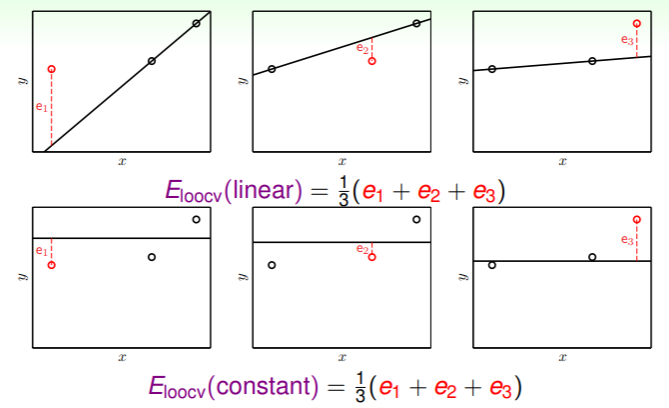
• 自然，要选取最小 $E_{loocv}$ 的直线作为估计，那就应当选取来自 ${\mathcal{H}}_{{\Phi }_0}$ 的常数直线。

现在，我们考虑 $E_{loocv}(\mathcal{H},\mathcal{A})$ 究竟与 $E_{out}(g)$ 有怎样的关系？在数据集 $\mathcal{D}$ 上，留一交叉验证法的错误评估的期望可以如下运算：

$$\begin{array}{rl}\underset{\mathcal{D}}{\mathbb{E}}\left(E_{loocv}(\mathcal{H},\mathcal{A})\right)=\underset{\mathcal{D}}{\mathbb{E}}\left(\frac{1}{N}\sum _{n=1}^N{e}_n\right)& =\frac{1}{N}\sum _{n=1}^N\underset{\mathcal{D}}{\mathbb{E}}(e_n)\\ & =\frac{1}{N}\sum _{n=1}^N\underset{{\mathcal{D}}_{train}}{\mathbb{E}}(e_n)+\underset{{\mathcal{D}}_{val}}{\mathbb{E}}(e_n)\\ & =\frac{1}{N}\sum _{n=1}^N\underset{{\mathcal{D}}_n}{\mathbb{E}}\left(\underset{({\mathbf{x}}_n,y_n)}{\mathbb{E}}(\text{err}(g_n^{-}({\mathbf{x}}_n),y_n)\right)\\ & =\frac{1}{N}\sum _{n=1}^N\underset{{\mathcal{D}}_n}{\mathbb{E}}{E}_{out}(g_n^{-})\\ & =\frac{1}{N}\sum _{n=1}^N\overline{E_{out}}(N-1)\\ & =\overline{E_{out}}(N-1)\end{array}$$

，因此我们可以说，留一交叉验证法的错误评估与 $E_{out}(g^{-})$ 在期望上相同，这在 ML 中称为 almost unbiased estimate of $E_{out}(g)$ （即无偏估计）

我们看看实践中留一交叉验证法的效果：

• 在老问题手写数字识别中，我们判断一个数是否为 1 ，通过根据 $E_{in}$ 选取估计函数和通过 $E_{loocv}$ 选取估计函数，有以下图像：
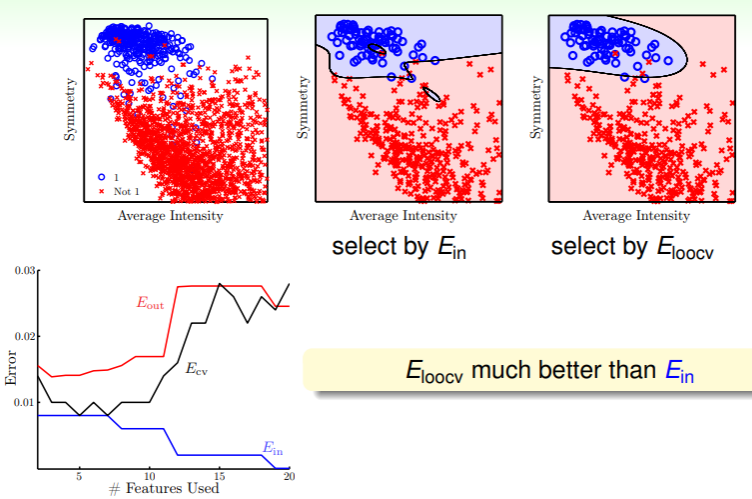
• 可以看到，随着特征选取的数量增加，$E_{in}$ 显著降低，而 $E_{out}$ 也随之呈增加趋势；
• 并且，$E_{loocv}$ 曲线总体趋势与 $E_{out}$ 相同，并且二者差距甚小，这也就表明用交叉验证的方法估计 $E_{out}$ 确实可行，
• 并且在特征选取低于 10 个时，$E_{in}$ 、$E_{out}$ 、$E_{loocv}$ 都总体处于较低值；

练习：计算留一交叉验证法的错误概率

V-Fold Cross Validation

留一交叉验证法是一种极端的交叉验证方法，其验证集的选取仅有 1 个样本，这其实本质上相当于将规模为 N 的数据集 $\mathcal{D}$ 分成了 N 份，其中每一份都有可能被选取、用于验证，因此有如下弊端：

• 每个模型都至多需要做 N 次训练，这在实际操作中导致的额外时间复杂度常常难以接受；（除非是类似线性回归这样有公式解的特殊模型）
• 由于一个样本点的验证结果差距通常悬殊（比如二元分类里 0 与 1），因此总体虽然经过平均，但还是有可能导致稳定性问题，例如上图中 $E_{loocv}$ 中波动的那些区域；

因此留一交叉验证虽然提供了很好的验证思路，但是在实践中并不实用。实际上为了降低额外计算的时间，我们借用留一交叉验证的思路，但是扩大其验证集：

• 将数据集 $\mathcal{D}$ 分成 $V$ 份，取出其中一份作为验证，剩余 $V-1$ 份用于训练，然后交叉验证，统计最后的交叉验证错误率：
• 这就是 V-Fold cross-validation ，在实践中，通常选取 $V=10$ ；

关于交叉验证，有以下几点需要牢记：

1. V-Fold 交叉验证比留一交叉验证使用更广泛、效果更佳，
2. 交叉验证通常也比单次验证能够得到更准确的结果，
3. 不过即使交叉验证，也比实际测试时的估计更乐观，所以不要因为“自欺欺人”而真的认为交叉验证反映了真实的情况；

练习：计算 10-Fold 交叉验证