10-Linear-Support-Vector-Machine

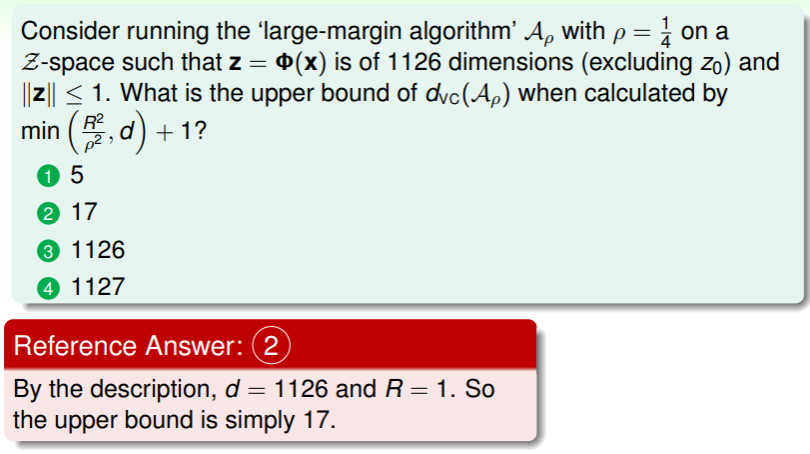
Large-Margin Separating Hyperplane

What is the Best Hyperplane?

在线性分类问题中我们学习了 pocket 算法，我们可以使用这两种算法在线性可分数据集上找到正确的分类器，但由于 PLA 遇错更新 的特点，找到哪一个分类器是随机的：

• 

那么哪个分类器是最好的呢？这里，我们必须要考虑数据集（包括测试集）中有噪音的问题，并且 噪音通常服从正态分布 ：

• 因此数据样本到分类器的最小距离越远，代表着对噪音的容忍度越高，而 噪音又与过拟合问题 密切相关，因此离所有数据样本都远的分类器应对过拟合现象的健壮性越好：
• 上图中从两个角度分析了样本到分类器的最小距离，因此第三个分类器的健壮性最好，是最优的分类器；
• 在 ML 中这样的“数据样本到分类器的最小距离”称为 margin ，即分类器的边。

因此要找到最好的分类器，我们可以将其数学化为以下的描述：

$$\underset{\mathbf{w}}{\max }\text{ margin}(\mathbf{w})\text{ s.t. }\{\begin{array}{l}\text{every }{y}_n{\mathbf{w}}^T{\mathbf{x}}_n>0,\\ \\ \text{margin}(\mathbf{w})=\underset{n=1,2,...,N}{\min }\text{distance}({\mathbf{x}}_n,\mathbf{w})\end{array}$$

即，分类器既要正确地实现分类，又要保证 margin 最大。

练习：找到 largest-margin 的分类器

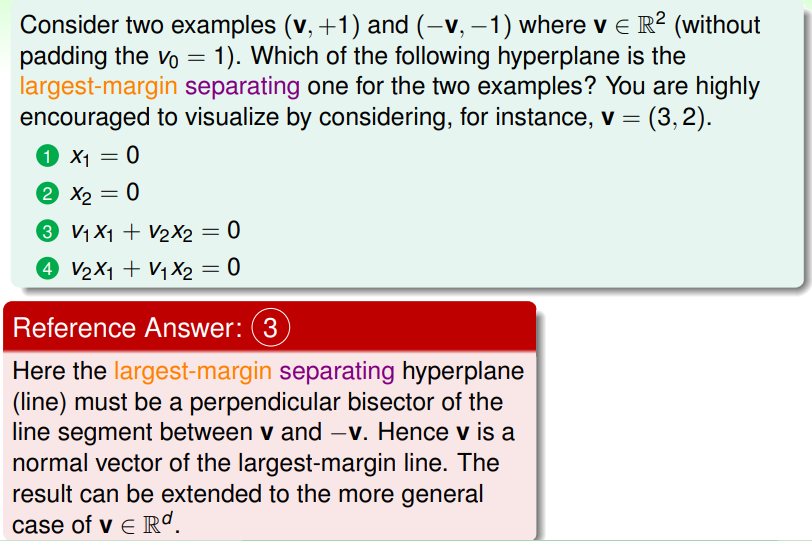
Standardize Largest-Margin Problem

在进一步简化这个找到最大 margin 的问题之前，我们对之前的符号做一些调整：

• 《基石》中设置权重向量中有一个特殊的维度 $w_0$ ，在这里我们将其分离出来，单独称作 $b$ ，而特征向量中 $x_0$ 则删去；
• 在这里假设函数形式如下：$h(\mathbf{x})=\text{sign}({\mathbf{w}}^T\mathbf{x}+b)$ ；

现在，我们先对 $\text{distance}(\mathbf{x},b,\mathbf{w})$ 函数进行一些探讨：

• 对于分类器（hyperplane），我们设置其函数为 ${\mathbf{w}}^T\mathbf{x}+b=0$ ，因此对任意两个分类器上的样本点 ${\mathbf{x}}^{{}^{\prime }}$ 和 ${\mathbf{x}}^{{}^{\prime \prime }}$ ，都可以构成一条 ${\mathbf{x}}^{{}^{\prime }}\to {\mathbf{x}}^{{}^{\prime \prime }}$ 的向量，并且有 ${\mathbf{w}}^T{\mathbf{x}}^{{}^{\prime }}=-b$ 、${\mathbf{w}}^T{\mathbf{x}}^{{}^{\prime \prime }}=-b$ ，
• 从而 ${\mathbf{w}}^T({\mathbf{x}}^{{}^{\prime }}-{\mathbf{x}}^{{}^{\prime \prime }})=0$ ，这意味着向量 $\mathbf{w}$ 是垂直于分类器的：
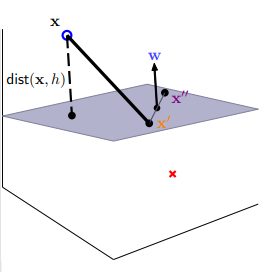
• 因此距离函数可以看作是两点函数在垂直方向上的投影（project）：$\text{distance}(\mathbf{x},b,\mathbf{w})=\left|\frac{{\mathbf{w}}^T}{||\mathbf{w}||}(\mathbf{x}-{\mathbf{x}}^{{}^{\prime }})\right|=\frac{1}{||\mathbf{w}||}|{\mathbf{w}}^T\mathbf{x}+b|$ ，
• 而对于线性分类问题，正确的分类会使得 label 与距离同号，因此可以脱去绝对值：$\text{distance}({\mathbf{x}}_n,b,\mathbf{w})=\frac{1}{||\mathbf{w}||}{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)$ ；

因此，现在我们可以将选取最佳分类器的问题描述为：

$$\underset{b,\mathbf{w}}{\max }\text{ margin}(b,\mathbf{w})\text{ s.t. }\{\begin{array}{l}\text{every }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)>0,\\ \\ \text{margin}(b,\mathbf{w})=\underset{n=1,2,...,N}{\min }\frac{1}{||\mathbf{w}||}{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\end{array}$$

而对于分类器 ${\mathbf{w}}^T\mathbf{x}+b=0$ 其与 $3{\mathbf{w}}^T\mathbf{x}+3b=0$ 的不同只是等比例放缩，因此同样的道理，我们可以将 $\underset{n=1,2,...,N}{\min }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)$ 放缩为 1 ，即 $\underset{n=1,2,...,N}{\min }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)=1$ ，此时 margin 函数的形式就变成 $\text{margin}(b,\mathbf{w})=\frac{1}{||\mathbf{w}||}$ ，因此原来的问题经过放缩后就变为：

$$\underset{b,\mathbf{w}}{\max }\frac{1}{||\mathbf{w}||}\text{ s.t. }\underset{n=1,2,...,N}{\min }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)=1$$

这里能够舍去第一个条件 $\text{every }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)>0$ 的限制的原因是放缩为 1 的过程中必然要满足。

进一步地，考虑 $\underset{n=1,2,...,N}{\min }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)=1$ 可以如何简化？我们可以用反证法证明，其可以放宽为 $y_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\ge 1$ ，但同时这个等号必然会成立：

• 

最后，要求得 $\frac{1}{||\mathbf{w}||}$ 最大，就要 $||\mathbf{w}||$ 最小，而 $||\mathbf{w}||=\sqrt{{\mathbf{w}}^T\mathbf{w}}$ ，因此最终我们可以得到对最佳分类器的选择问题描述为：

$$\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\text{ s.t. }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\ge 1,\text{for all }n$$

（这里冒出一个 $\frac{1}{2}$ 虽然很突兀，但在下文有所解释）

练习：理解到分类器的距离

Support Vector Machine

What is Support Vector ?

为了求解这个标准问题，我们考虑一种简单情形：现有四个样本点，分别特征向量和标签为：

$$\mathrm{X}=\left[\begin{array}{c}00\\ 22\\ 20\\ 30\end{array}\right],\mathbf{y}=\left[\begin{array}{c}-1\\ -1\\ +1\\ +1\end{array}\right]$$

，因此待定系数求解分类器的方程组为：

$$\{\begin{array}{l}-b\ge 1,\\ -2w_1-2w_2-b\ge 1,\\ 2w_1+b\ge 1,\\ 3w_1+b\ge 1\end{array}$$

，最终可以解得 $w_1\ge +1,w_2\le -1$ ，这样就有 ${\mathbf{w}}^T\mathbf{w}\ge 2$ ，上文我们在这个权重向量的内积前多乘了一个 $\frac{1}{2}$ ，这样就得到 $\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\ge 1$ 。

因此要使得 $\frac{1}{2}{\mathbf{w}}^T\mathbf{w}$ 最小，即等于 1 ，此时可以解得 $w_1=1,w_2=-1,b=-1$ ，即分类器的数学表达形式为 $g_{\text{SVM}}(\mathbf{x})=\text{sign}(x_1-x_2-1)$ 。等等，哪里蹦出一个 SVM ？

• 在这个特殊情形中，四个样本点中有三个处于边界上，它们到分类器的距离为 $\frac{1}{||\mathbf{w}||}=\frac{1}{\sqrt{2}}$ ：
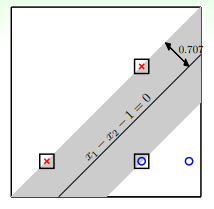
• 在这类问题中只有处于边界上的点才有考虑的价值，因此 ML 中称为 support vector （这里其实只是候选 candidate ，这个会在后续课程解释，这里只需要了解）
• 因此所谓 support vector machine ，就是可以从 largest-margin hyperplanes 中学习的模型；

General SVM: QP problem

不过从这个特殊情形向一般化推广比较麻烦，我们可以先从问题的特征入手：

$$\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\text{ s.t. }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\ge 1,\text{for all }n$$

这里 SVM 的数学形式是一个二次函数，参数为 $(b,\mathbf{w})$ ，其受线性条件约束，条件的参数也是 $(b,\mathbf{w})$ ，这类问题称为 Quadratic Programming 问题，已有前人做了详尽的实现，我们现在只需要套用：

• 左边是我们现在的问题，右边是常规 QP 问题的一般形式，因此只要找到我们问题中什么对应 QP 问题的 $Q,p,A,c$ 四个参数，然后代入 QP solver 中运算即可：
• QP solver 的实现方案在各类 ML 平台/框架上都有实现，比如：
  • LIBSVM - A Library for Support Vector Machines
  • GitHub - qpsolvers: Quadratic programming solvers in Python

另外我们需要知道这里谈论的 SVM 实际上是一种 hard-margin 、linear 的模型，即边界是硬性规定的、样本空间是线性的。若要得到非线性的 SVM？那就使用特征转换吧！

练习：找到 QP solver 的参数

Reasons behind Large-Margin Hyperplane

Constraint and Minimize Target

联系之前学习的 正则化 和现在的 SVM ，我们从它们命题中的限制与最小化的目标考量，可以做如下对比：

• 
• 可以看出，SVM 与正则化的限制条件和最小化目标正好相反，也许可以认为 SVM 是限制 $E_{in}=0$ 的特殊的正则化。

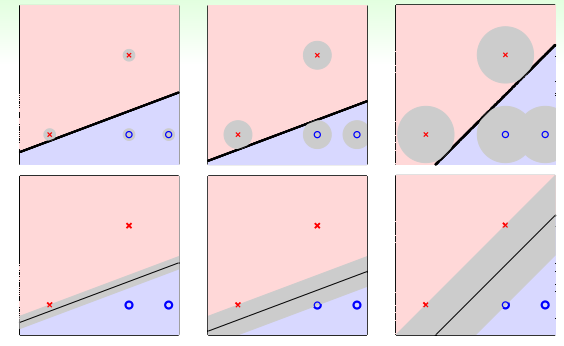
从另一个角度，我们记 SVM 的学习算法为 ${\mathcal{A}}_{\rho }$ ，其含义是最后返回的假设 $g$ 满足 $\text{margin}(g)\ge \rho$ ，

• 显然，当 $\rho =0$ ，SVM 就退化为 PLA ，而 PLA 可以 shatter 的样本数与维度的关系 是 $N=d+1$ ：
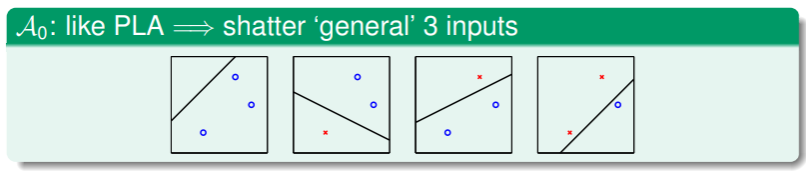
• 但随着 $\rho$ 的增大，SVM 对可以 shatter 的样本数进行了限制：
• 这表明 SVM 的 margin 越大，dichotomy 的数量越少，有效 VC dimension 的维数越小，从而 $E_{in}$ 与 $E_{out}$ 会 更加接近 ，从而能够获得更好的推广性；

VC Dimension of Learning Algorithm

现在我们提出在学习算法上的 VC dimension ，记作 $d_{VC}({\mathcal{A}}_{\rho })$ ，它是与输入样本直接相关的；而原来在 假设集上的 VC dimension $d_{VC}(\mathcal{H})$ 是与输入样本无关的，因此 $d_{VC}({\mathcal{A}}_{\rho })$ 更能准确地表现出对特定问题的复杂度：

• $d_{VC}({\mathcal{A}}_{\rho })$ 等于该学习算法 ${\mathcal{A}}_{\rho }$ 最多可以完全 shatter 的样本数；
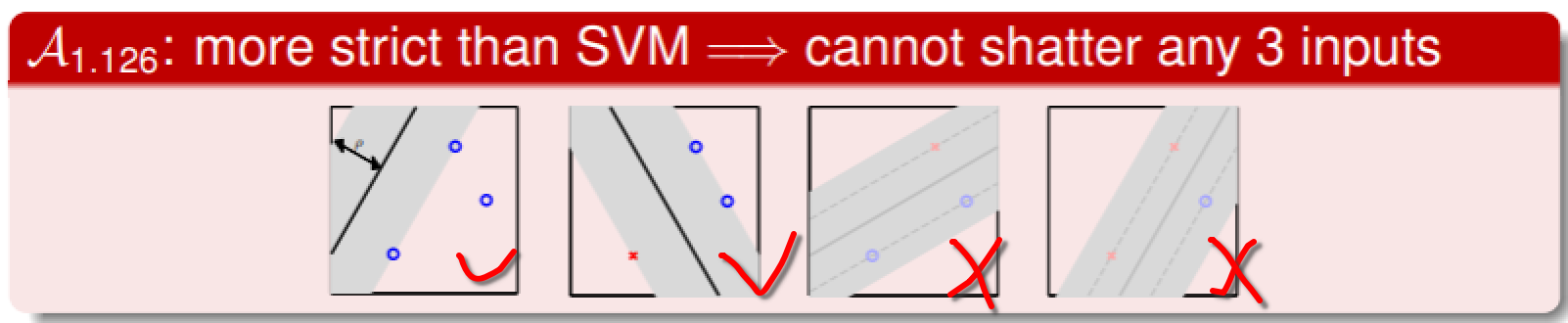
• 以一个特殊例子入手：我们在三个输入样本的问题里，并且该三个样本都位于一个单位圆上（注意任何三个点都可以唯一确定一个圆，并且这个圆可以随意放缩到单位圆，而三个点的相对位置不发生变化）：
  • 这三个点的相互最远距离不超过 $\sqrt{3}$ ，因此当 $\text{margin}>\frac{\sqrt{3}}{2}$ 时就不存在可以 shatter 三个点的假设；
• 更严格的证明可以得到： 这表明通过限制 $\rho$ 的大小，确实可以做到比 $d+1$ 更小的 VC dimension ；

SVM Advantages

我们最初学习的 PLA 算法得到的分类器是 hyperplane ，它的优势是数量较少，但是缺点的过于简单，对很多问题不能做到 $E_{in}$ 足够小；后面我们利用特征转换改进 PLA ，于是它能够应对更复杂的问题，不过随之数量骤增。这两者的关系似乎恰类鱼与熊掌，不可兼得。

现在我们提出了 SVM ，它能够通过设置 margin 限制数量，又可以保证是线性模型，我们只要在线性 SVM 的基础上引入特征转换，就可以保证数量不会太多，且能适应复杂情况的能力更强：

• 

练习：计算学习算法的 VC dimension 上限