A1-String-Exercise

11-3 练习构造各算法的查询表

index:         0   1   2   3   4
P[i]:          M   I   A   M   I
next[i]:      -1   0   0   0   1
imp-next[i]:  -1   0   0  -1   0
bc[i]:         3   4   2   3   4
ss[i]:         0   2   0   0   5
gs[i]:         3   3   3   5   1

index:         0   1   2   3   4   5   6
P[i]:          B   A   R   B   A   R   A  
next[i]:      -1   0   0   0   1   2   3
imp-next[i]:  -1   0   0  -1   0   0   3
bc[i]:         3   6   5   3   6   5   6
ss[i]:         0   1   0   0   1   0   7
gs[i]:         7   7   7   7   7   2   1

index:         0   1   2   3   4   5   6   7   8   9
P[i]:          C   I   N   C   I   N   N   A   T   I
next[i]:      -1   0   0   0   1   2   3   0   0   0
imp-next[i]:  -1   0   0  -1   0   0   0   0   0   0
bc[i]:         3   9   6   3   9   6   6   7   8   9
ss[i]:         0   1   0   0   1   0   0   0   0  10
gs[i]:        10  10  10  10  10  10  10  10   5   1

index:         0   1   2   3   4   5   6   7   8   9  10  11
P[i]:          P   H   I   L   A   D   E   L   P   H   I   A
next[i]:
imp-next[i]:
bc[i]:
ss[i]:
gs[i]:

11-4 KMP 复杂度分析

[! note] 课本 11.3.7 的性能分析

由上可见，KMP 算法借助 next 表可避免大量不必要的字符比对操作，但这意味着渐进意义上的时间复杂度会有实质改进吗？这一点并非一目了然，甚至乍看起来并不乐观。比如就最坏情况而言，共有 Ω(n) 个对齐位置，而且在每一对齐位置都有可能需要比对多达 Ω(m) 次。

如此说来，难道在最坏情况下，KMP 算法仍可能共需执行 Ω(nm) 次比对？不是的。以下更为精确的分析将证明，即便在最坏情况下，KMP 算法也只需运行线性的时间！ 为此，请留意 KMP代码 中用作字符指针的变量 i 和 j。若令 k = 2i - j 并考查 k 在 KMP 算法过程中的变化趋势，则不难发现：while 循环每迭代一轮，k 都会严格递增。

实际上，对应于 while 循环内部的 if-else 分支，无非两种情况：

• 若转入 if 分支，则 i 和 j 同时加一，于是 k = 2i - j 必将增加；
• 反之若转入 else 分支，则尽管 i 保持不变，但在赋值 j = next[j] 之后 j 必然减小，于是 k = 2i - j 也必然会增加。

纵观算法的整个过程：启动时有 i = j = 0，即 k = 0；算法结束时 i<=n 且 j>=0，故有 k <= 2n。在此期间尽管整数 k 从 0 开始持续地严格递增，但累计增幅不超过 2n，故 while 循环至多执行 2n 轮。

另外，while 循环体内部不含任何循环或调用，故只需 O (1) 时间。因此，若不计构造 next 表所需的时间，KMP 算法本身的运行时间不超过 O (n)。也就是说，尽管可能有Ω(n)个对齐位置， 但就分摊意义而言，在每一对齐位置仅需 O (1)次比对。

既然 next 表构造算法的流程与 KMP 算法并无实质区别，故仿照上述分析可知，next 表的构造仅需 O (m)时间。综上可知，KMP 算法的总体运行时间为 O (n + m)。

说明：为评估 KMP 算法的效率，课本 11.3.7 节引入一个随迭代过程严格单调递增的观察量 k = 2i - j，从而简捷地证明了迭代次数不可能超过 O(n)。这一初等的证明虽无可辩驳，但毕竟未能直观地展示出其不计算成本之间的本质联系。 试证明，在算法执行的整个过程中：

1. 观察量 i 始终等于已经做过的成功比对（含与最左端虚拟通配符的“比对”）次数；
2. 观察量 i - j 始终不小于已经做过的失败比对次数。

反观 KMP 主算法，循环中 if 判断语句的两个分支，分别对应于题中所定义的成功和失败比对。

• 其中，只有成功的分支会修改观察量 i——更准确地说，观察量 i 加一，当且仅当当前的比对是成功的。考虑到观察量 i 的初始值为 0，故在整个算法过程中，它始终忠实地记录着成功比对的次数。
• 观察量 i - j 的初始值也是 0。对于成功分支，变量 i 和 j 会同时递增一个单位，故 i - j 的 数值将保持不变。而在失败分支中，首先观察量 i 保持不变。另一方面，因为必有： next[j] < j 故在将变量 j 替换为 next[j] 之后，观察量 i - j 亦必严格单调地增加。

综合以上两种情况，观察量 i - j 必然可以作为失败比对次数的上界。

11-5 二维 bc[][] 表

说明：针对坏字符在模式串 P 中位置太靠右，以至位移量为负的情况，11.4.2 节建议的处理方法是直接将 P 右移一个字符。然而如图所示，此后并不能保证原坏字符位置能够恢复匹配。为此，或许你会想到：可在 P[j] 的左侧找到最靠右的字符’X’，并将其与原坏字符对齐，即构造二维 bc[][] 表：

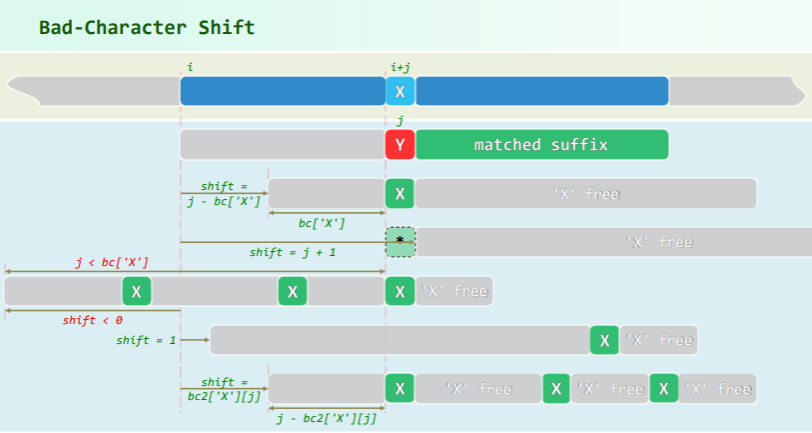
• 为什么不倾向于使用这种方法？ 尽管以上思路的实现方式可能不尽相同，但本质上都等效于将原先一维的 bc[] 表，替换为二维的 bc[][] 表。具体地，这是一张 m * |Σ| 的表格，其中 bc[j]['X'] 指向“在 P[j] 左侧并与之最近的字符 'X'”。

如此，尽管预处理时间和所需空间的增长量并不大，但匹配算法的逻辑控制却进一步复杂化。 最重要的是，此类二维 bc[][] 表若能发挥作用，则当时的好后缀必然很长——此类情况，同时使用的 gs[] 表完全可以替代 bc[][] 表。

11-6 gs[] 构造算法的时间复杂度

证明：

1. ==buildSS() 过程的运行时间为 O (m)==

int* buildSS ( char* P ) { //构造最大匹配后缀长度表：O(m)
	int m = strlen ( P ); int* ss = new int[m]; //Suffix Size表
	ss[m - 1]  =  m; //对最后一个字符而言，与之匹配的最长后缀就是整个P串
// 以下，从倒数第二个字符起自右向左扫描P，依次计算出ss[]其余各项
	for ( int lo = m - 1, hi = m - 1, j = lo - 1; j >= 0; j -- )
	    if ( ( lo < j ) && ( ss[m - hi + j - 1] < j - lo ) ) //情况一
	        ss[j] =  ss[m - hi + j - 1]; //直接利用此前已计算出的ss[]
	    else { //情况二
	        hi = j; lo = min ( lo, hi );
	        while ( ( 0 <= lo ) && ( P[lo] == P[m - hi + lo - 1] ) ) //二重循环？
	            lo--; //逐个对比处于(lo, hi]前端的字符
	        ss[j] = hi - lo;
	    }
	return ss;
}

该算法的运行时间，主要消耗于其中的“两重”循环。

暂且忽略内（while）循环，首先考查外（for）循环。若将 j 视作其控制变量，则不难验证：

1. j 的初始值为 m - 2
2. 每经过一步迭代，j 都会递减一个单位
3. 在其它的任何语句中，j 都没有作为左值被修改
4. 一旦 j 减至负数，外循环随即终止

由此可知，外循环至多迭代 O(m)步，累计耗时不超过 O(m)。 尽管从表面的形式看，外循环的每一步都有可能执行一趟内循环，但实际上所有内循环的累计运行时间也不超过 O(m)。为此，只需将 lo 视作其控制变量，即不难验证：

• lo 的初始值为 m - 1
• 每经过一步内循环的迭代，lo 都会递减一个单位
• 在其它部分，lo 只在 lo = __min(lo, hi) 一句中作为左值被修改，但 仍是非增
• 一旦 lo 减至负数，内循环就不再启动

由此可知，内循环累计至多迭代 O(m)步，相应地累计耗时不超过 O(m)。 综合以上两项，即得题中结论。

2. ==buildGS() 的运行时间为 O (m)== 仿照 1) 中的分析技巧。只要以 j 作为外循环的控制变量，则可知外循环至多迭代 O(m)步， 耗时 O(m)；以 i 作为内循环的控制变量，则可知内循环累计至多迭代 O(m)步，累计耗时 O(m)。

11-7 模式枚举问题：匹配间隔的设置对复杂度的影响

说明：模式枚举(pattern enumeration)类应用中，需要从文本串 T 中找出所有的模式串 P (|T| =n,|P| =m)，并且有时允许模式串的两次出现位置之间相距不足 m 个字符。如在 000000 中查找 000，若限制多次出现的模式串之间至少相距|P| =3 个字符，则应找到 2 处匹配，若不限制则找到 4 处匹配。

1. 举例说明，采用不做限制的匹配，BM-GS 算法可能需要Ω(nm)时间 将题中所举实例一般化，取模式串 P = “00…0”，|P| = m，则 P 对应的 gs[] 表应如下：

  j   0 1 2 3 4 ... m - 2 m - 1
gs[j] 1 2 3 4 5 ... m - 1   m 

再取文本串 T = “00000…0”，|T| = n >> m。 于是自然地，在每一对齐位置，经过 m 次比对之后都可以找到一次完全匹配。然而接下来，只能右移 gs[0] = 1 位并重新对齐，经过 m 次比对之后方可找到下一次完全匹配。

如上过程将反复进行，直到文本串被扫描完毕。整个过程共有 n - m + 1 个对齐位置，而且在每个位置都需要经过 m 次比对，方可发现一次完全匹配。鉴于 n 和 m 取值的任意性，在此类最坏情况下，该算法的累计耗时量应为： $(n-m+1)\ast m=\Theta (nm)$

以上实例仍然非常极端，更具一般性的例子则如图 x11.1所示。 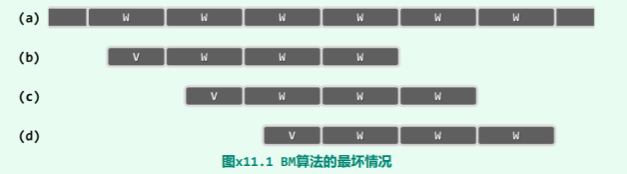这里以两个基本的字符串 W 和 V 作为“积木”。为简化起见，假定字符串 W 中的彼此字符互异，|W| = w 为常数；V 是 W 的一个非空后缀，|V| = v <= w。文本串 T 如图(a)所示，由 n/w 个 W 顺次串接而成。模式串 P 如图(b)所示，由一个 V 和(m - v)/w 个 W 顺次串接而成。当然，与通常情况 一样，这里也有2 << m << n。

于是，P 对应的 gs[] 表应如下：

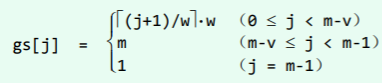其中特别地，有： gs[0] = w 因此，在每次发现一个完全匹配后，P 都会右移 w 位并与 T 重新对齐，然后找到下一个完全匹配。 如此，总共会有 n/w 个对齐位置（各对应于一个完全匹配）；而重要的是，每次对齐之后都需要经过 m 次比对。由此可见，整个过程所做比对的次数累计为： $\frac{n}{w}\times m=\Theta (nm)$

2. 针对这一缺陷改进 BM-GS 策略，使之即便采用不限制举例的约定时，最坏情况下也只需线性时间。 反观以上一般性实例可见，其中模式串 P 每一次右移，都属于如图所示的情况：

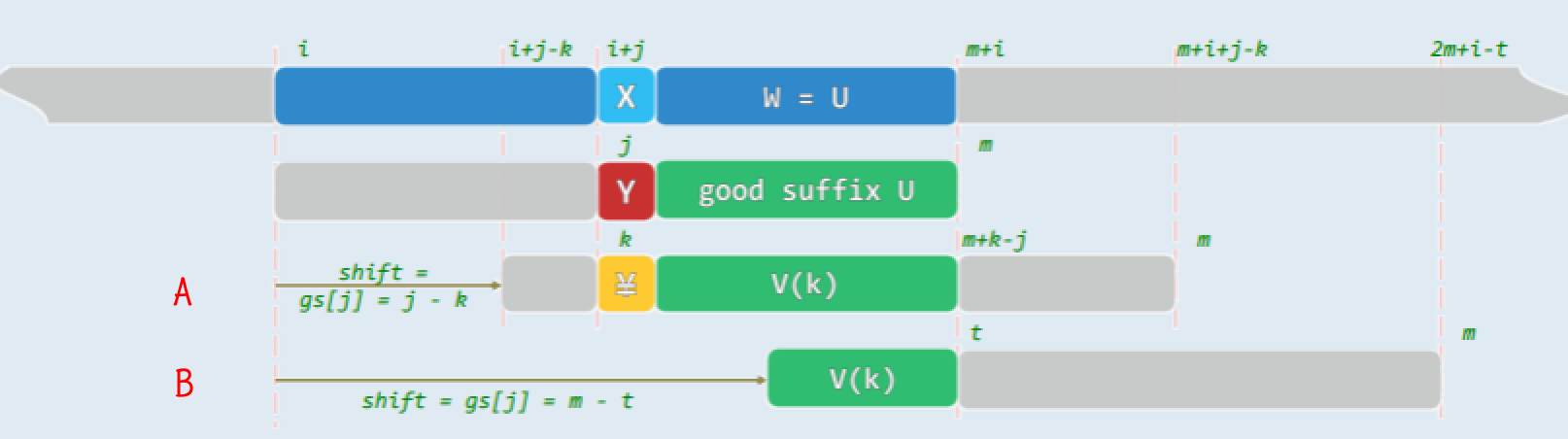
在前一轮比对中，成功次数过多，以致好后缀过长（甚至如上例，就是 P 整体）。

这里的技巧是，在此类对齐位置，不必一直比对至 P 的最左端。实际上不难看出，一旦自右向左比对到原文本串 T 中好后缀的最右端，即可马上判定是否完全匹配。仍以图 x11.1为例，除了第一轮比对，在后续的各轮比对中，均只需比较模式串 P 中最靠右的 w 个字符——根据 gs[] 表的定义，其余的 m - w 个字符必然是匹配的。

利用这一所谓的 Galil 规则加以改进之后，文本串 T 的每个字符都不再会重复接受比对。既然累计不超过线性次比对，总体耗时也就不致超过线性的规模。

11-9 分析蛮力算法的实际效率

实现：版本 1

/************************************************
 * Text :  0 1 2 . . . i-j . . . i . . . . . n-1
 *         ------------|---------|------------
 * Pattern:            0 . . . . j . .
 *                     |---------|
 ************************************************/

int match ( char* P, char* T ) { //串匹配算法（Brute-force-1）
	size_t n = strlen ( T ), i = 0; //文本串长度、当前接受比对字符的位置
	size_t m = strlen ( P ), j = 0; //模式串长度、当前接受比对字符的位置
	while ( j < m && i < n ) //自左向右逐个比对字符
	    if ( T[i] == P[j] ) //若匹配
	        { i ++;  j ++; } //则转到下一对字符
	    else //否则
	        { i -= j - 1; j = 0; }//T串回退、P复位
	return i - j; //最终的对齐位置：藉此足以判断匹配结果
}

指向原始笔记的链接

实现：版本 2

/************************************************
 * Text :  0 1 2 . . . i i+1 . . . i+j . . n-1
 *         ------------|-----------|------------
 * Pattern  :          0 1  .  .   j . .
 *                     |-----------|
 *************************************************/
int match ( char* P, char* T ) { //串匹配算法（Brute-force-2）
	size_t n = strlen ( T ), i = 0; //文本串长度、与模式串首字符的对齐位置
	size_t m = strlen ( P ), j; //模式串长度、当前接受比对字符的位置
	for ( i = 0; i < n - m + 1; i++ ) { //文本串从第i个字符起，与
	    for ( j = 0; j < m; j++ ) //模式串中对应的字符逐个比对
	        if ( T[i + j] != P[j] ) break; //若失配，模式串整体右移一个字符，再做一轮比对
        }
	    if ( j >= m ) break; //找到匹配子串
	}
	return i; //最终的对齐位置：藉此足以判断匹配结果
}

两个版本是等价的。

指向原始笔记的链接

假定所有字符出现的概率均等，试证明

1. P 与 T 在每一对齐位置，需连续执行恰好 k 次字符比对操作的概率为 $\frac{s-1}{s^k}$;

任意字符比对的成功概率和失败概率分别为 $\frac{1}{s}$ 和 $\frac{s-1}{s}$，其中 s=|Σ|为字符集的规模。 恰好执行 k 次字符对比，当且仅当前 k - 1次成功，但最后一次失败。根据 伯努利分布， 这类事件发生的概率应为：${\left(\frac{1}{s}\right)}^{k-1}\cdot \frac{s-1}{s}=\frac{s-1}{s^k}$

2. P 与 T 的每一对齐位置，需连续执行字符比对操作的期望次数不超过 $\frac{s}{s-1}\le 2=O(1)$ 由 1) 的分析结论，每一次字符比对都可视作一次伯努利实验（Bernoulli trial），成功与失败的概率分别为 1/s 和 (s - 1)/s ；而每趟比对的次数 X，则符合几何分布（geometric distribution）——亦即，其中前 X-1次实验成功的概率各为 1/s，最终一次实验失败的概率为 (s - 1)/s。因此，X 的期望值不超过 s/(s - 1)。直接由期望值的定义出发，也可得出同样结论。

具体地，连续执行字符比对操作的期望次数，应该就是所有可能的次数，关于其对应概率的加权平均，亦即：

$$\sum _{k=1}^{m}k\cdot \frac{s-1}{s^k}=(s-1)\cdot \sum _{k=1}^m\frac{k}{s^k}\le (s-1)\cdot \sum _{k=1}^{\infty }\frac{k}{s^k}=\frac{s}{s-1}$$

11-10 BM 算法和 KMP 算法分别擅长于处理何种类型的字符串？

正如教材第11.4.5节所指出的，在评价不同串匹配算法各自的实用范围时，在不同应用中 单次比对的成功概率，扮演着重要的角色。而根据 习题[11-9] 的分析结论，在通常的情况下，这一概率首先并直接取决于字符集的规模。

• 当字符集规模较小时，单次比对的成功概率较高，蛮力算法的效率较低。此时，KMP 算法稳定的线性复杂度，更能体现出优势；而采用 BC 表的 BM 算法，却并不能大跨度地向前移动。
• 反之，若字符集规模较大，则单次比对的成功概率较小，
  • 蛮力算法也能接近于线性的复杂度。
  • 此时，KMP 算法尽管依然保持线性复杂度，但相对而言的优势并不明显；
  • 而采用 BC 表的 BM 算法， 则会因比对失败的概率增加，可以大跨度地向前移动。