30-Kernel-Support-Vector-Machine

Kernel Trick

上节课我们通过提出 SVM 的对偶模型 Dual SVM ，实现了对空间维数 $\tilde{d}$ 依赖的减少，但 并没有完全祛除 ：

• 
• 在 SVM 中，在经过特征转换到一维空间后，才能正确使用 SVM 模型，因此特征转换和向量内积这两部分操作的耗时，将直接与空间维数 $\tilde{d}$ 相关，达到 $\mathcal{O}(\tilde{d})$ 的复杂度；

Decrease Complexity by Kernel Function

这样拆分成两步的操作必然会带来 $\mathcal{O}(\tilde{d})$ 的复杂度，因此要降低复杂度，我们必须深入探讨：

• 考虑在二维空间中的特征转换：
• 仔细观察特征转换+内积这个组合操作的运算过程，我们可以分离出内积 ${\mathbf{x}}^T{\mathbf{x}}^{{}^{\prime }}$ ，最终可以实现将 $\mathcal{O}(d^2)$ 的复杂度降低到 $\mathcal{O}(d)$ ；

这样一步完成特征转换+向量内积的过程称为 kernel function ，每个特定的转换都对应特定的 kernel function ：

• 
• 因此，计算 QP 问题中矩阵 $Q_D$ 可以写为：$q_{n,m}=y_n{y}_m{\mathbf{z}}_n^T{\mathbf{z}}_m=y_n{y}_{m}K({\mathbf{x}}_n,{\mathbf{x}}_m)$ ，由 kernel function 完成关键的转换与内积运算；
• 并且，回顾求解 $b$ 的过程，也可以运用 kernel function 进行简化：$b=y_s-{\mathbf{w}}^T{\mathbf{z}}_s=y_s-{\left(\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n\right)}^T{\mathbf{z}}_s=y_s-\sum _{n=1}^N{\alpha }_n{y}_n\left(K({\mathbf{x}}_n,{\mathbf{x}}_m)\right)$
• 同理，我们对最佳假设 $g_{SVM}$ 也可以如此处理：$g_{SVM}(\mathbf{x})=\text{sign}({\mathbf{w}}^T\Phi (\mathbf{x})+b)=\text{sign}\left(\sum _{n=1}^N{\alpha }_n{y}_{n}K({\mathbf{x}}_n,\mathbf{x})+b\right)$
• 这些操作都运用到称为 kernel trick 的技巧，即通过高效的 kernel function 避免对空间维数 $\tilde{d}$ 的依赖，
• 并且最终呈现出的 $q_{n,m},b,g_{SVM}$ 三者的计算都仅依赖于输入样本 ${\mathbf{x}}_n$ ；

Kernel SVM

在之前讨论的 SVM 模型中再加入 kernel function ，我们就得到了 Kernel SVM ：

• 
• 使用 QP 问题求解 Kernel SVM 的过程就如上图，
• 其中值得注意的是，经过 kernel function ，计算 $q_{n,m}$ 的运算复杂度最终降低到 $\mathcal{O}(N^2)$ ，计算 $b$ 和 $g_{SVM}$ 的复杂度降低到 $\mathcal{O}(\text{nums of SV})$ ，并且完全摆脱了对空间维数 $\tilde{d}$ 的依赖；

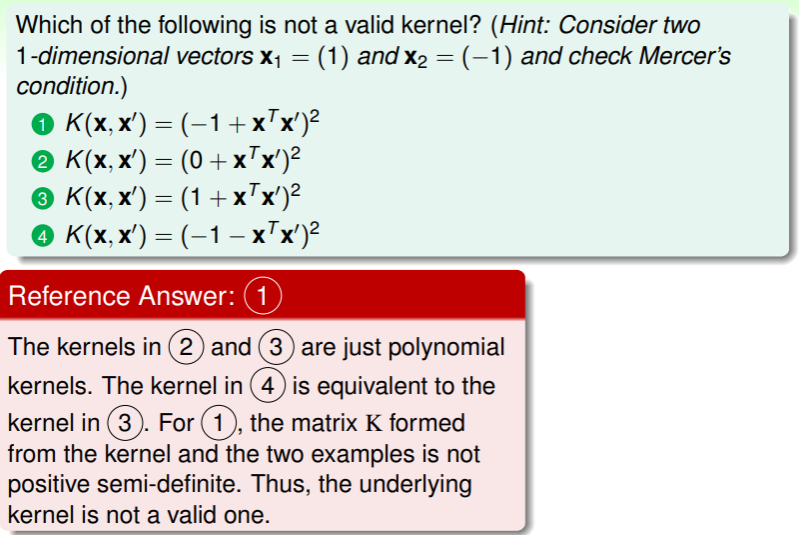
练习：计算 kernel function

Polynomial Kernel

上节我们学到了 kernel function 在特定特征转换和向量内积中起作用的例子，现在我们对特征转换进行一些放缩，以便获得更简洁的 kernel function 形式：

• 
• 第三种转换形式，可以使 kernel function 的形式转换为 $K_2(\mathbf{x},{\mathbf{x}}^{{}^{\prime }})=(1+\gamma {\mathbf{x}}^T{\mathbf{x}}^{{}^{\prime }}{)}^2\text{ with }\gamma >0$ ，显然转换后的 kernel function 在计算上要更加简单；

Effects of Parameters on Polynomial Kernel

不过这种转换除了计算简单外，还有什么实际意义吗？实际上，放缩导致内积的结果不同，进而导致 SVM 的几何形态不同——进而影响 SV 的数量：

• 
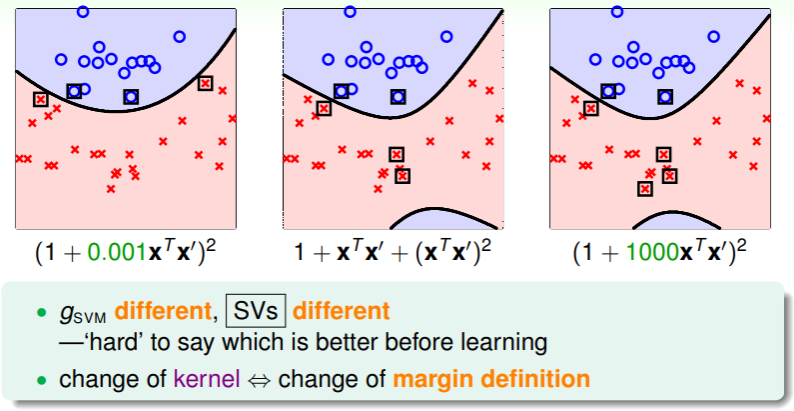
• 因此选择 kernel function 也是同特征转换 $\Phi$ 一样值得细细考量的事情；

进一步地在不同空间中推广 kernel function ，并且特征转换函数 ${\Phi }_Q$ 有两个特殊的参数：$\zeta ,\gamma$ ，这两个参数体现在 kernel function 中如下：

• 
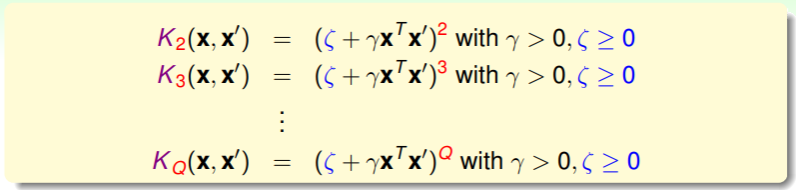
• 另外，我们可以通过限制 margin 的宽度，来 限制复杂度 ，使得即是在高维转换中复杂度也不是太高：
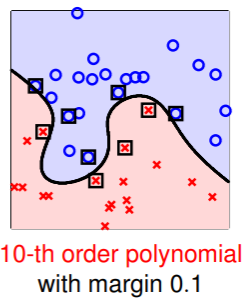
• 这样加入多项式形式的 kernel function 的 SVM，简称为 Polynomial SVM；

Linear Kernel

在通用的多项式形式的 kernel function 中，有一个特殊例子值得考虑：

• 
• 对于一维转换的 kernel function ，只需要用到向量内积，因此其又称作 linear kernel ，它的重要性在于我们的原则——从简单的线性模型做起，逐步提高复杂程度，避免过拟合风险；

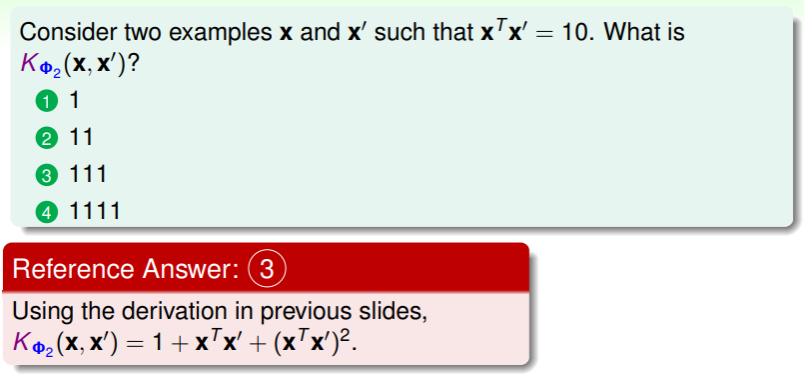
练习：理解二维 kernel function 的一般形式推导

Gaussian Kernel

我们前面的操作都是在降维，以便利用已经熟悉的线性模型对降维后的数据进行正确处理。那么反之，我们如何使用线性模型，能够确保它通过一定的特征转换后，能处理高维甚至无穷多维的数据呢？

Introduction of Gaussian Function

Gaussian Function

一般形式为 $f(x)=e^{-x^2}$ ，带参数的形式为 $f(x)=a\cdot e^{-\frac{(x-b{)}^2}{2c^2}}$ 。

通常用于随机变量正态分布的概率密度函数，此时对应的函数形式为

$$g(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}$$

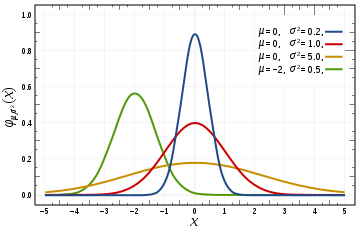
函数图像大致如下：

结合 kernel function ，要找到无穷多维的特征转换函数 $\Phi (\mathbf{x})$ ，我们只要找到对应的可高效计算的 $K(\mathbf{x},{\mathbf{x}}^{{}^{\prime }})$ 即可。这里要用到的，就是 高斯函数，我们要从一维模型拓展到多维模型，即对输入样本 $\mathbf{x}=(x)$ ，kernel function 应为：

$$K(x,x^{{}^{\prime }})=e^{-(x-x^{{}^{\prime }}{)}^2}$$

于是我们可以展开指数中的二次项，并对其中 $x{x}^{{}^{\prime }}$ 项进行泰勒展开：

$$\begin{array}{rl}K(x,x^{{}^{\prime }})& =e^{-(x{)}^2}{e}^{-(x^{{}^{\prime }}{)}^2}{e}^{2x{x}^{{}^{\prime }}}\\ & =e^{-(x{)}^2}{e}^{-(x^{{}^{\prime }}{)}^2}\left(\sum _{1=0}^{\infty }\frac{(2x{x}^{{}^{\prime }}{)}^i}{i!}\right).........\text{(Tayor Expansion)}\\ & =\sum _{i=0}^{\infty }\left(e^{-(x{)}^2}{e}^{-(x^{{}^{\prime }}{)}^2}\sqrt{\frac{2^i}{i!}}\cdot \sqrt{\frac{2^i}{i!}}(x{)}^i(x^{{}^{\prime }}{)}^i\right)\\ & =\Phi (x{)}^T\Phi (x^{{}^{\prime }})\end{array}$$

其中无限维的特征转换函数 $\Phi (x)=e^{-x^2}\cdot \left(1,\sqrt{\frac{2}{1!}}x,\sqrt{\frac{2^2}{2!}}{x}^2,...\right)$ 。

Gaussian Kernel and SVM

更一般的，加入高斯函数的 Gaussian Kernel 的数学形式写作：

$$K(\mathbf{x},{\mathbf{x}}^{{}^{\prime }})=e^{-\gamma ||\mathbf{x}-\mathbf{x}|{|}^2},\text{ with }\gamma >0$$

于是，使用 Gaussian Kernel 的 SVM 的假设可以写为：

$$\begin{array}{rl}{g}_{SVM}(\mathbf{x})& =\text{sign}\left(\sum _{SV}{\alpha }_n{y}_{n}K({\mathbf{x}}_n,\mathbf{x}+b\right)\\ & =\text{sign}\left(\sum _{SV}{\alpha }_n{y}_n{e}^{-\gamma ||\mathbf{x}-{\mathbf{x}}_n|{|}^2+b}\right)\end{array}$$

这个假设的含义是中心在 SV 上（即 $\mu ={\mathbf{x}}_n$ ）的高斯函数的线性组合，又称为 Raidal Basis Function（RBF，径向基函数）kernel 。于是，Gaussian SVM 的真实作用，就是找到正确的 ${\alpha }_n$ ，以实现对 SV 上的高斯函数的线性组合，从而将一维的样本映射到无穷多维空间中。

Role of Gaussian SVM

回想我们 前文 提到 SVM 的目标就是通过 margin 限制分类器 hyperplane 的数量不过多、并且也能应对足够复杂的样本情况：

• 
• 回顾我们学习 ML 模型的过程，先是学习了 hyperplane，然后为了应对非线性情形，我们引入了特征转换，现在我们通过 kernel trick ，可以更高效地实现特征转换，即可以不必找到确切的转换函数 $\mathbf{z}=\Phi (\mathbf{x})$ ，而是找到对应的 kernel function 即可：$K(\mathbf{x},{\mathbf{x}}^{{}^{\prime }})$ ；
• 另外我们也通过 large margin 来限制复杂度，使其不过于庞大，从而可以使得 SVM 可以处理复杂的非线性问题、又不至于复杂度过高；
• 并且我们也不必非得存储 $\mathcal{Z}$ 空间中最优的权重向量 $\mathbf{w}$ ，而是只需要存储能够表现 $\mathbf{w}$ 的少量的 SV 和对应的 ${\alpha }_n$ 即可；

Overfitting Risk of Gaussian SVM

于是，通过 Gaussian SVM ，我们可以实现无穷多维的分类，并且通过 large margin ，可以实现对这种模型可用性的确保。不过事情显然还没结束，我们对 Gaussian Kernel 中的假设有一个关键参数 $\gamma$ ，它会如何影响模型呢？

• 
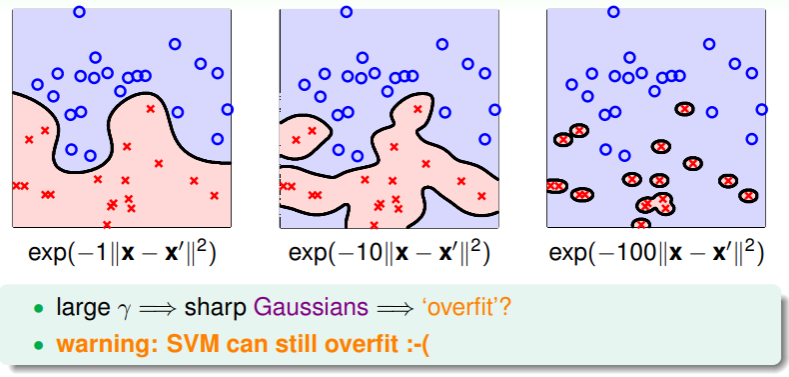
• 因此，我们在使用 Gaussian SVM 时，仍然要小心地设置 $\gamma$ 的值；
• 毕竟 large margin 只是确保可行性，但没有确保效果究竟如何。

练习：$\gamma \to +\infty$ 时会发生什么？

Comparison of Kernels

现在我们对学习过的 kernel function 进行优劣总结，方便后续建模时直接使用。

Pros and Cons of Different Kernels

对于 Linear Kernel ，

• 
• 其优势在于拟合安全（发生过拟合风险很低）、计算高效（特制的 QP solver 可以高效地实现计算）、可解释性强（可以很容易地分析出权重向量 $\mathbf{w}$ 和支持向量 SV 的含义是什么）
• 其缺点就是不能应对非线性可分的数据集；
• 因此 Linear Kernel 可以作为第一手使用的选择，根据表现情况进行修改或选用更复杂的 kernel 。

对于 Polynomial Kernel ，

• 
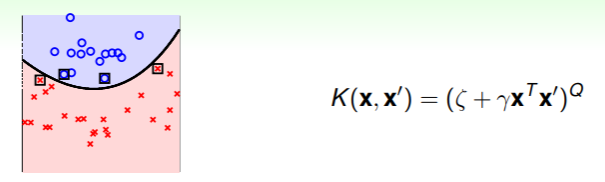
• 其优势在于能够应对非线性数据集，并且对空间维数 $Q$ 的掌控力更强，能够自如地应对各种空间的特征转换；
• 其缺点是对于高维空间时，$|\zeta +\gamma {\mathbf{x}}^T{\mathbf{x}}^{{}^{\prime }}|$ 这个多项式的值计算出的结果要么很大、要么很小，必须经过额外的放缩操作才能利用；另外参数需要确定 $\gamma ,\zeta ,Q$ 这三个，因此比较难以选择；
• 因此建议在 $Q$ 较小时使用。

对于 Gaussian Kernel ，

• 
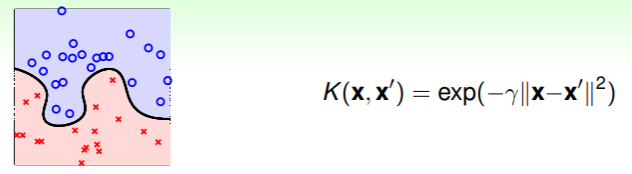
• 其优势是最为 powerful 的一种 kernel function，并且高斯函数本身是有界的函数，因此不会导致数值过大的问题，另外仅需要确定一个参数，即 $\gamma$ ，这样操作起来比较简单；
• 其缺点是计算结果中不会直接给出 $\mathbf{w}$ ，这样的话解释性比较弱，就像一个黑盒；另外运算效率较低，并且由于过于 powerful，因此过拟合风险较高；
• 尽管如此，Gaussian Kernel 仍是最常用的 kernel function ，只是要千万小心使用。

Customized Kernel

除此之外，我们可以自己定制 kernel function 吗？回想 kernel function 的含义，其通过向量内积 $\Phi (\mathbf{x}{)}^T\Phi ({\mathbf{x}}^{{}^{\prime }})$ 找到样本之间的联系，因此我们定制 kernel 的目标也是找到这种联系：

• 
• 具体参考：Mercer’s theorem - Wikipedia ；

练习：找到合理的 kernel