12-Instances-of-recursion

Hanoi 问题

描述：法国数学家 Edouard Lucas 于 1883 提出的 Hanoi 塔问题，可形象地描述如下：

有 n 个中心带孔的圆盘贯穿在直立于地面的一根柱子上，各圆盘的半径自底而上不断缩小；
需要利用另一根柱子将它们转运至第三根柱子，但在整个转运的过程中，游离于这些柱子之外的圆盘不得超过一个 (即每次只能取一个)，且每根柱子上圆盘半径都须保持上小下大。试将上述转运过程描述为递归形式，并而实现一个递归算法。

递归版

将三根柱子分别记作 X、Y 和 Z，则整个转运过程可递归描述为：

为将 X 上的 n 个盘子借助 Y 转运至 Z，只需（递归地）
- 将 X 上的 n - 1 个盘子借助 Z 转运至 Y
- 再将 X 上最后一个盘子直接转移到 Z
- 最后再将 Y 上的 n - 1 个盘子借助 X 转运至 Z

按照这一理解，即可如下所示实现对应的递归算法：

// 按照Hanoi规则，将柱子Sx上的n只盘子，借助柱子Sy中转，移到柱子Sz上

void hanoi ( int n, Stack<Disk>& Sx, Stack<Disk>& Sy, Stack<Disk>& Sz ) {
	if ( n > 0 ) { //没有盘子剩余时，不再递归
		hanoi ( n - 1, Sx, Sz, Sy ); //递归：将Sx上的n - 1只盘子，借助Sz中转，移到Sy上
		move ( Sx, Sz ); //直接：将Sx上最后一只盘子，移到Sz上
		hanoi ( n - 1, Sy, Sx, Sz ); //递归：将Sy上的n - 1只盘子，借助Sx中转，移到Sz上
	}
}

关于时间复杂度，该算法对应的边界条件和递推式为： T(1) = O(1) T(n) = 2T(n - 1) + O(1)

若令: S(n) = T(n) + O(1) 则有: S(1) = O(2) S(n) = 2∙S (n - 1) = 2^2 ∙ S(n - 2) = 2^3 ∙ S(n - 3) = … = 2^(n-1) ∙ S(1) = 2n

故有： T(n) = O(2^n)

迭代版

// Iterative Algorithm
1. Calculate the total number of moves required 
	i.e."pow(2, n)- 1" here n is number of disks.

2. If number of disks (i.e. n) is even then interchange destination pole and auxiliary pole.

3. for i = 1 to total number of moves:
    if i%3 == 1:
	    legal movement of top disk between source pole and destination pole
    if i%3 == 2:
	    legal movement top disk between source pole and auxiliary pole    
    if i%3 == 0:
        legal movement top disk between auxiliary pole and destination pole

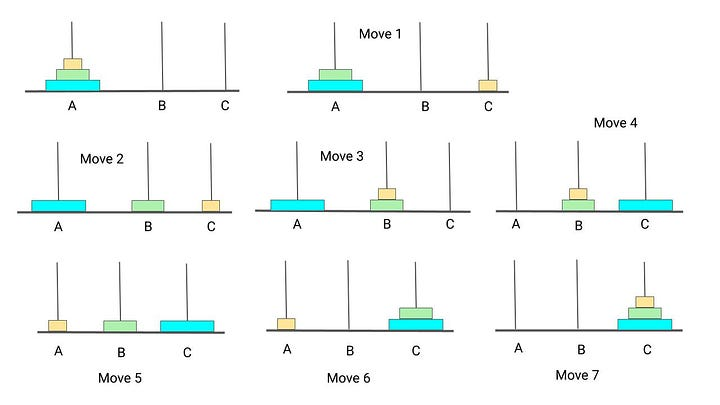
Let us understand with a simple example with 3 disks: So, total number of moves required = 2^3-1 = 7
When i=1, (i % 3 == 1) legal movement between ‘A’ and ‘C’
When i=2, (i % 3 == 2) legal movement between ‘A’ and ‘B’
When i=3, (i % 3 == 0) legal movement between ‘B’ and ‘C’
When i=4, (i % 3 == 1) legal movement between ‘A’ and ‘C’
When i=5, (i % 3 == 2) legal movement between ‘A’ and ‘B’
When i=6, (i % 3 == 0) legal movement between ‘B’ and ‘C’
When i=7, (i % 3 == 1) legal movement between ‘A’ and ‘C’
So, after all these destination poles contains all the in order of size.
After observing above iterations, we can think that after a disk other than the smallest disk is moved, the next disk to be moved must be the smallest disk because it is the top disk resting on the spare pole and there are no other choices to move a disk.

// C++ Program for Iterative Tower of Hanoi using STL

#include <iostream>
#include <vector>
#include <stack>
using namespace std;

char rod[]={'S', 'A', 'D'};
vector<stack<int>> stacks(3); // 3 stacks for 3 rods

void moveDisk(int a, int b)
{
	if (stacks[b].empty() || (!stacks[a].empty() && stacks[a].top() < stacks[b].top()))
	{
		cout << "Move disk " << stacks[a].top() << " from rod " << rod[a] << " to rod " << rod[b] << "\n";
		stacks[b].push(stacks[a].top());
		stacks[a].pop();
	}
	else
		moveDisk(b, a);
}

void towerOfHanoi(int n)
{
	cout << "Tower of Hanoi for " << n << " disks:\n";

	int src = 0, aux = 1, dest = 2;
	for (int i = n; i > 0; i--)
		stacks[src].push(i);

	int totalMoves = (1 << n) - 1;
	if (n % 2 == 0)
		swap(aux, dest);

	for (int i = 1; i <= totalMoves; i++)
	{
		if (i % 3 == 0)
			moveDisk(aux, dest);
		else if (i % 3 == 1)
			moveDisk(src, dest);
		else
			moveDisk(src, aux);
	}
}

int main()
{
	int n = 3; // number of disks
	towerOfHanoi(n);
	return 0;
}

References

Related Articles

References:
http://en.wikipedia.org/wiki/Tower_of_Hanoi#Iterative_solution

八皇后问题

八皇后问题

问题描述

国际象棋中皇后的势力范围覆盖其所在的水平线、垂直线以及两条对角线。现考查如下问题：在 n x n 的棋盘上放置 n 个皇后，如何使得她们彼此互不攻击——此时称她们构成一个可行的棋局。对于任何整数 n >= 4，这就是 n 皇后问题。由鸽巢原理可知，在 n 行 n 列的棋盘上至多只能放置 n 个皇后。反之，n 个皇后在 n x n 棋盘上的可行棋局通常也存在，比如图 b 即为在 8 x 8 棋盘上，由 8 个皇后构成的一个可行棋局。

皇后的实现
struct Queen { //皇后类
	int x, y; //皇后在棋盘上的位置坐标
	Queen ( int xx = 0, int yy = 0 ) : x ( xx ), y ( yy ) {};
	bool operator== ( Queen const& q ) const { //重载判等操作符，以检测不同皇后之间可能的冲突
	return ( x == q.x ) //行冲突（这一情况其实并不会发生，可省略）
			|| ( y == q.y ) //列冲突
			|| ( x + y == q.x + q.y ) //沿正对角线冲突
			|| ( x - y == q.x - q.y ); //沿反对角线冲突
}

bool operator!= ( Queen const& q ) const { 
	return ! ( *this == q ); } //重载不等操作符
};
算法实现

基于试探回溯策略，可如代码所示，实现通用的 N 皇后算法：
void placeQueens ( int N ) { //N皇后算法（迭代版）：采用试探/回溯策略，借助栈记录查找的结果
	Stack<Queen> solu; //存放（部分）解的栈
	Queen q ( 0, 0 ); //从原点位置出发
	do { //反复试探、回溯
		if ( N <= solu.size() || N <= q.y ) { //若已出界，则
			q = solu.pop(); q.y++; //回溯一行，并继续试探下一列
		} else { //否则，试探下一行
			while ( ( q.y < N ) && ( 0 <= solu.find ( q ) ) ) //通过与已有皇后的比对
			{ q.y++; nCheck++; } //尝试找到可摆放下一皇后的列
			if ( N > q.y ) { //若存在可摆放的列，则
				solu.push ( q ); //摆上当前皁后，并
				if ( N <= solu.size() ) nSolu++; //若部分解已成为全局解，则通过全局变量nSolu计数
				q.x++; q.y = 0; //转入下一行，从第0列开始，试探下一皇后
			}
		}
	} while ( ( 0 < q.x ) || ( q.y < N ) ); //所有分支均已或穷举或剪枝后，算法结束
}
既然每行能且仅能放置一个皇后，故不妨首先将各皇后分配至每一行。然后，从空棋盘开始，逐个尝试着将她们放置到无冲突的某列。每放置好一个皇后，才继续试探下一个。若当前皇后在任何列都会造成冲突，则后续皇后的试探都必将是徒劳的，故此时应该回溯到上一皇后。

这里借助栈 solu 来动态地记录各皇后的列号。当该栈的规模增至 N 时，即得到全局解。该栈即可依次给出各皇后在可行棋局中所处的位置。

实例

首先试探第一行皇后，如图 (a)所示将其暂置于第 0 列，同时列号入栈。接下来试探再第二行皇后，如图 (b)所示在排除前两列后，将其暂置于第 2 列，同时列号入栈。然而此后试探第三行皇后时，如图 (c)所示发现所有列均有冲突。于是回溯到第二行，并如图 (d)所示将第二行皇后调整到第 3 列，同时更新栈顶列号。后续各步原理相同，直至图 (l)栈满时得到一个全局解。

如此不断地试探和回溯，即可得到所有可行棋局。可见，通过剪枝我们对原规模为 4! = 24 的搜索空间实现了有效的筛选。随着问题规模的增加，这一技巧的优化效果将更为明显。
指向原始笔记的链接

迷宫问题

迷宫寻径

问题描述

路径规划是人工智能的基本问题之一，要求依照约定的行进规则，在具有特定几何结构的空间区域内，找到从起点到终点的一条通路。以下考查该问题的一个简化版本：空间区域限定为由 n x n 个方格组成的迷宫，除了四周的围墙，还有分布其间的若干障碍物；只能水平或垂直移动。我们的任务是，在任意指定的起始格点与目标格点之间，找出一条通路（如果的确存在）。

迷宫格点实现
typedef enum { AVAILABLE, ROUTE, BACKTRACKED, WALL } Status; //迷宫单元状态
//原始可用的、在当前路径上的、所有转向均尝试失败后回溯过的、不可使用的（墙）
typedef enum { UNKNOWN, EAST, SOUTH, WEST, NORTH, NO_WAY } ESWN; //单元的相对邻接方向
//未定、东、南、西、北、无路可通

inline ESWN nextESWN ( ESWN eswn ) { return ESWN ( eswn + 1 ); } //依次转至下一邻接方向

struct Cell { //迷宫格点
	int x, y; Status status; //x坐标、y坐标、类型
	ESWN incoming, outgoing; //进入、走出方向
};

#define LABY_MAX 24 //最大迷宫尺寸
Cell laby[LABY_MAX][LABY_MAX]; //迷宫
可见，除了记录其位置坐标外，格点还需记录其所处的状态。共有四种可能的状态：

原始可用的（AVAILABLE）、

在当前路径上的（ROUTE）、

所有方向均尝试失败后回溯过的（BACKTRACKED）、

不可穿越的（WALL）。

属于当前路径的格点，还需记录其前驱和后继格点的方向。既然只有上、下、左、右四个连通方向，故以 EAST、SOUTH、WEST 和 NORTH 区分。特别地，

因尚未搜索到而处于初始 AVAILABLE 状态的格点，邻格的方向都是未知的（UNKNOWN）；

经过回溯后处于 BACKTRACKED 状态的格点，与邻格之间的连通关系均已关闭，故标记为 NO_WAY。

邻格查询

在路径试探过程中需反复确定当前位置的相邻格点，可如代码所示实现查询功能。
inline Cell* neighbor ( Cell* cell ) { //查询当前位置的相邻格点
	switch ( cell->outgoing ) {
		case EAST : return cell + LABY_MAX; //向东
		case SOUTH : return cell + 1; //向南
		case WEST : return cell - LABY_MAX; //向西
		case NORTH : return cell - 1; //向北
		default : exit ( -1 );
	}
}
邻格转入

在确认某一相邻格点可用之后，算法将朝对应的方向向前试探一步，同时路径延长一个单元。为此，需如代码所示实现相应的格点转入功能。
inline Cell* advance ( Cell* cell ) { //从当前位置转入相邻格点
	Cell* next;
	switch ( cell->outgoing ) {
		case EAST: next = cell + LABY_MAX; next->incoming = WEST; break; //向东
		case SOUTH: next = cell + 1; next->incoming = NORTH; break; //向南
		case WEST: next = cell - LABY_MAX; next->incoming = EAST; break; //向西
		case NORTH: next = cell - 1; next->incoming = SOUTH; break; //向北
		default : exit ( -1 );
	}
	return next;
}
寻径算法
// 迷宫寻径算法：在格单元s至t之间规划一条通路（如果的确存在）
	bool labyrinth ( Cell Laby[LABY_MAX][LABY_MAX], Cell* s, Cell* t ) {
	if ( ( AVAILABLE != s->status ) || ( AVAILABLE != t->status ) ) return false; //退化情况
	Stack<Cell*> path; //用栈记录通路（Theseus的线绳）
	s->incoming = UNKNOWN; s->status = ROUTE; path.push ( s ); //起点
	do { //从起点出发不断试探、回溯，直到抵达终点，或者穷尽所有可能
		Cell* c = path.top(); //检查当前位置（栈顶）
		if ( c == t ) return true; //若已抵达终点，则找到了一条通路；否则，沿尚未试探的方向继续试探
		while ( NO_WAY > ( c->outgoing = nextESWN ( c->outgoing ) ) ) //逐一检查所有方向
			if ( AVAILABLE == neighbor ( c )->status ) break; //试图找到尚未试探的方向
			if ( NO_WAY <= c->outgoing ) //若所有方向都已尝试过
				{ c->status = BACKTRACKED; c = path.pop(); }//则向后回溯一步
			else //否则，向前试探一步
				{ path.push ( c = advance ( c ) ); c->outgoing = UNKNOWN; c->status = ROUTE; }
		} while ( !path.empty() );
	return false;
}
该问题的搜索过程中，局部解是一条源自起始格点的路径，它随着试探、回溯相应地伸长、缩短。因此，这里借助栈 path 按次序记录组成当前路径的所有格点，并动态地随着试探、回溯做入栈、出栈操作。路径的起始格点、当前的末端格点分别对应于 path 的栈底和栈顶，当后者抵达目标格点时搜索成功，此时 path 所对应的路径即可作为全局解返回。

实例

左侧为随机生成的 13 x 13 迷宫。算法启动时，其中格点分为可用（AVAILABLE，白色）与障碍（WALL，黑色）两种状态。在前一类中，随机指定了起始格点（+）和目标格点（$)。中图为算法执行过程的某一时刻，可见原先为可用状态的一些格点已经转换为新的状态：转入 ROUTE 状态的格点，依次联接构成一条（尚未完成的）通路；曾参与构成通路但后因所有前进方向均已尝试完毕而回溯的格点，则进而从 ROUTE 转入 TRIED 状态（以圆圈注明）。如右图所示，经过 48 步试探和 6 步回溯，最终找到一条长度为 42 的通路。通过这一实例亦可看出，在起点与终点之间的确彼此连通时，尽管这一算法可保证能够找出一条通路，但却未必是最短的。

正确性和复杂度

该算法会尝试当前格点的所有相邻格点，因此通过数学归纳可知，若在找到全局解后依然继续查找，则该算法可以抵达与起始格点连通的所有格点。因此，只要目标格点与起始格点的确相互连通，则这一算法必将如右图所示找出一条联接于二者之间的通路。

从算法的中间过程及最终结果都可清晰地看出，这里用以记录通路的栈结构的确相当于忒修斯手中的线绳，它确保了算法可沿着正确地方向回溯。另外，这里给所有回溯格点所做的状态标记则等效于用粉笔做的记号，正是这些标记确保了格点不致被重复搜索，从而有效地避免了沿环路的死循环现象。

算法的每一步迭代仅需常数时间，故总体时间复杂度线性正比于试探、回溯操作的总数。由于每个格点至多参与试探和回溯各一次，故亦可度量为所有被访问过的格点总数——在图 4.10 中，也就是最终路径的总长度再加上圆圈标记的数目。
指向原始笔记的链接

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索

12-Instances-of-recursion

Hanoi 问题

递归版

迭代版

References

八皇后问题

八皇后问题

问题描述

皇后的实现

算法实现

实例

迷宫问题

迷宫寻径

问题描述

迷宫格点实现

邻格查询

邻格转入

寻径算法

实例

正确性和复杂度

关系图谱

目录

反向链接