11-ALU

组合逻辑与时序逻辑

门电路

组合逻辑

时序逻辑

存储电路

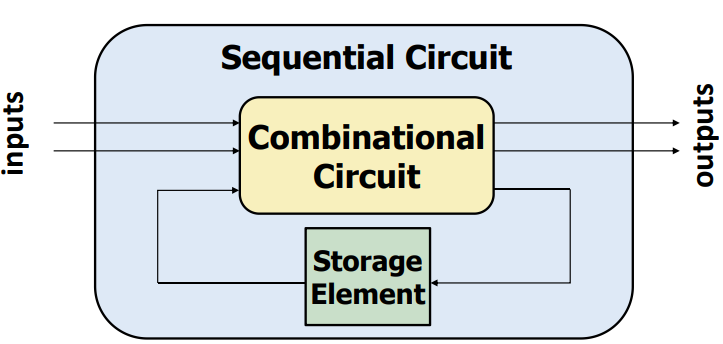
基本记忆单元

RS 锁存器

D 锁存器

D 触发器

算术运算及电路实现

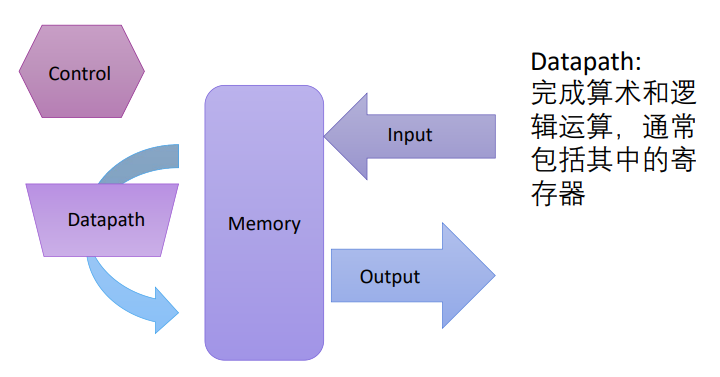
运算器功能

完成算术、逻辑运算
- - − × ÷ ∧ ∨ ¬
得到运算结果的状态
- C Z V S
取得操作数
- 寄存器组、数据总线
输出、存放运算结果
- 寄存器组、数据总线
暂存运算的中间结果
- Q 寄存器，移位寄存器
由控制器产生的控制信号驱动

实现运算功能的基础逻辑电路

逻辑门电路
- 完成逻辑运算
加法器
- 完成加法运算
触发器
- 保存数据
多路选择器、移位器
- 选择、连通

ALU 设计

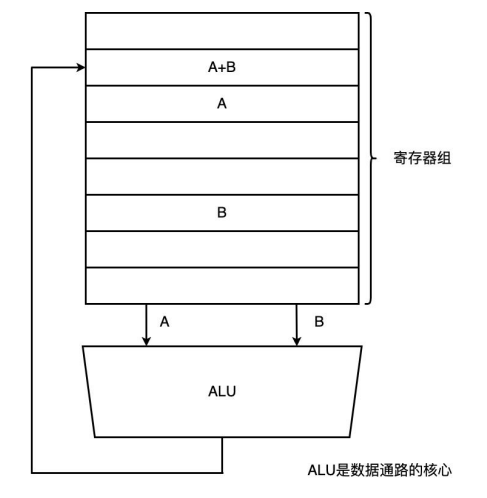
数据通路的图示。

ALU 的功能：

对操作数 A、B 完成算术逻辑运算

1 位全加器

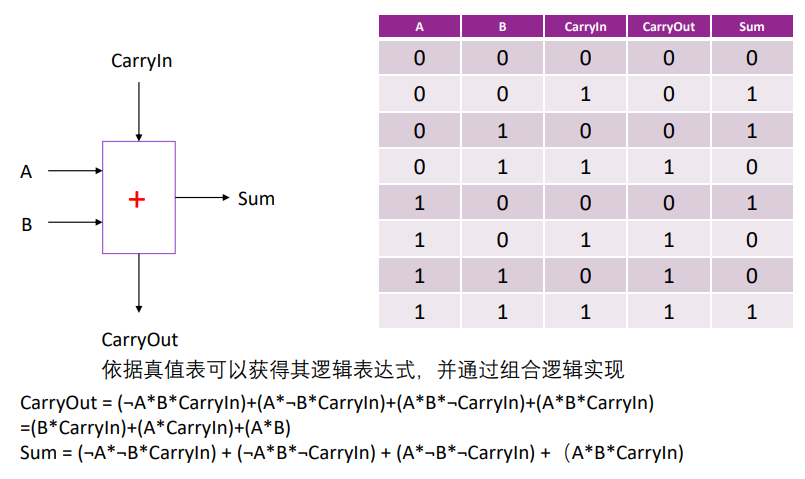
全加器

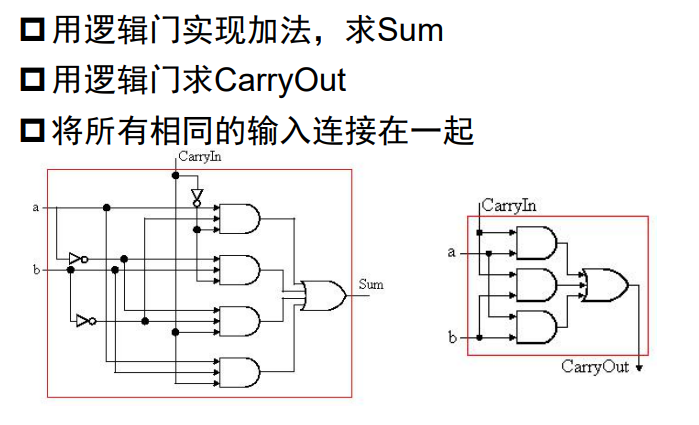
1 位 ALU

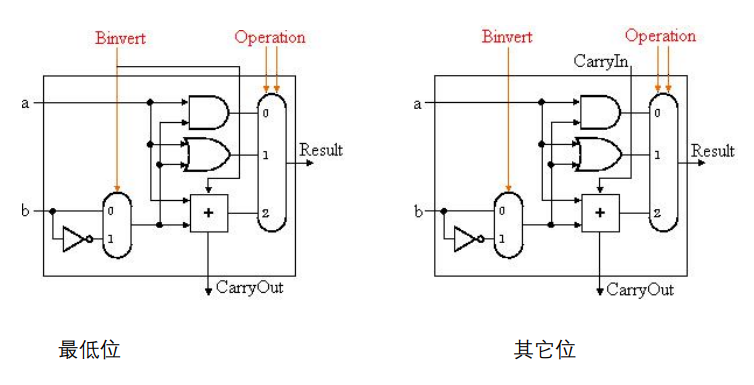设计过程:

确定 ALU 的功能
确定 ALU 的输入参数
根据功能要求得到真值表，获得逻辑表达式
依据逻辑表达式实现逻辑电路

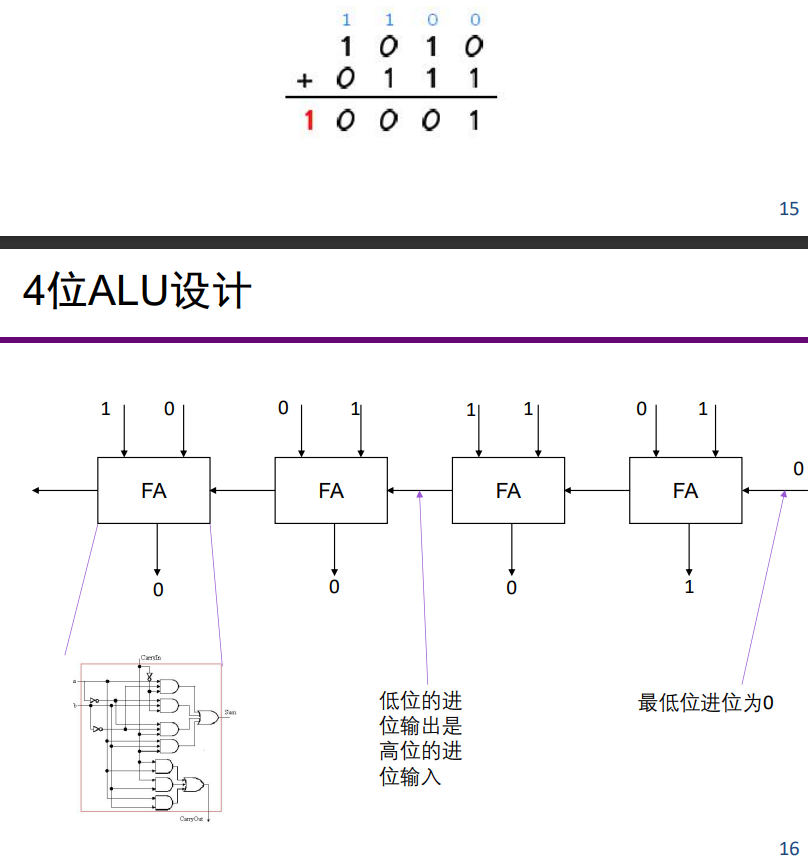
4 bits ALU

思路 1：同 1 位 ALU 设计，写真值表，逻辑表达式，通过逻辑电路实现
思路 2： n 使用 1 位 ALU 串联起来，得到 4 位 ALU

超前进位与结果标志

如何能提前得到 Cout? 显然

当 a=b=0 时，Cout=0
当 a=b=1 时，Cout=1
当 a=1, b=0 或 a=0, b=1 时候， Cout=Cin

通过单独的进位电路，可以同时得到计算结果和进位：

$P_{i} = a_{i} + b_{i}$
$G_{i} = a_{i} * b_{i}$

于是如此计算超前进位：

C1=a1b1 + (a1+b1)C0=G1+P1C0
C2=a2b2 + (a2+b2)C1=G2+P2G1+P2P1C0
C3=a3b3 + (a3+b3)C2=G3+P3G2+P3P2G1+P3P2 P1C0
C4=a4b4 + (a4+b4)C3=

其它 Flag 标志的计算：

Z=(F1=0)*(F2=0)*(F3=0)*(F4=0)
S=最高位
OV=¬F1*¬F2*S+F1*F2*¬S

算术运算的实现

补码运算

根据运算规则：

[a-b]补=[a]补+[-b]补
[-b]补 的补码为：将 [b]补 的各位取反，并加 1
由此可以使用加法器实现减法：
- 给定控制命令 C=0 作加法，C=1 做减法
- 使用选择器实现

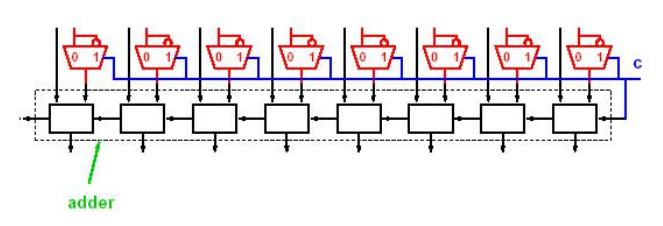
原码乘法

基本算法
- 若乘数的当前位 == 1，将被乘数和部分积求和
- 若乘数的当前为 == 0，则跳过
- 将部分积移位
- 所有位都乘完后，部分积即为最终结果
N位乘数 * M位被乘数 -> N+M 位的积
乘法显然比加法更加复杂，但是要比 10 进制乘法要简单

原码乘法 version 1: 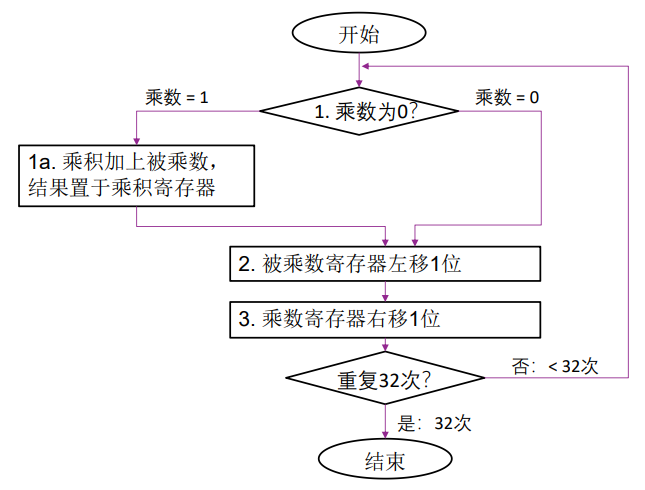原码乘法实现电路 1:

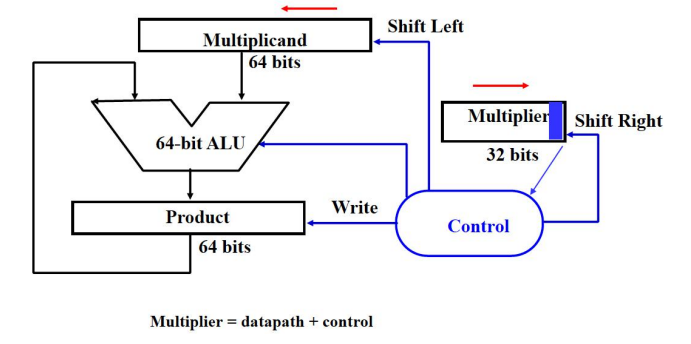
64-位被乘数寄存器，64-位 ALU，64-位部分积寄存器，32-位乘数寄存
不足：
- 被乘数的一半存储的只是 0，浪费存储空间；
- 每次加法实际上只有一半的位有效，浪费了计算能力；

原码乘法实现电路 2:

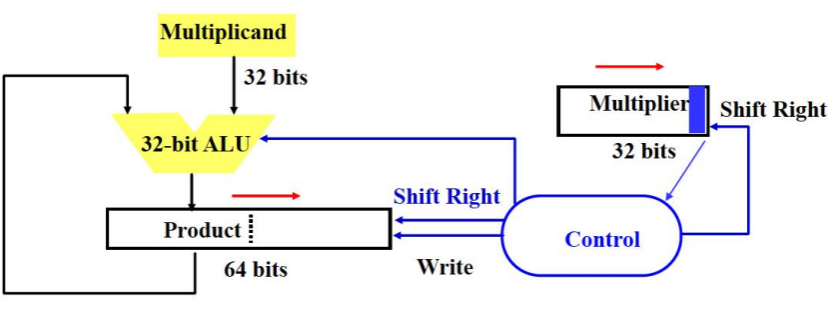
32 位被乘数寄存器，32 位 ALU，64 位部分积寄存器
改进之处：解决了对加法器位数的浪费

原码乘法实现电路 3:

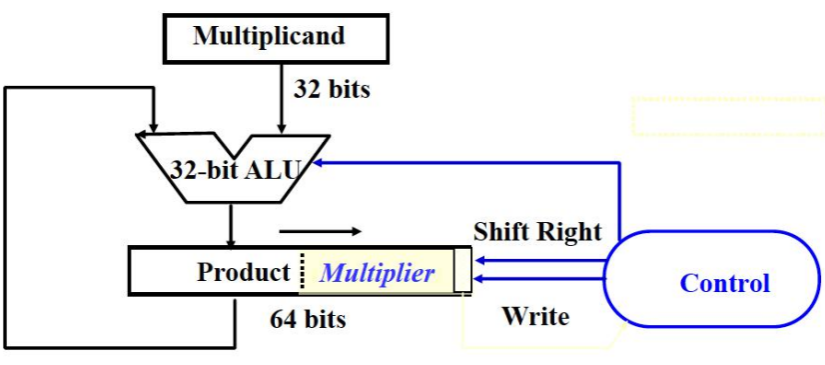
32 位被乘数寄存器，32 位 ALU，64 位部分积寄存器（0-位乘数寄存器）
不足：乘数寄存器也存在浪费的情况
- 把已经完成的乘数位移出，移入的是 0
- 解决这个浪费，可以把乘数和部分积低位结合起来

补码乘法

方案一：
- 将补码转换为原码绝对值，进行原码的正数乘法
- 依据以下原则得到符号位，并转换回补码表示：同号为正，异号为负
方案二：补码直接乘 —— 布斯算法

布斯算法的推导过程：

原理：虽然乘法是加法的重复，但也可以将它理解成加法和减法的组合
例如：十进制乘法 6 x 99 = 6 x 100 – 6 x 1 = 600 – 6 = 594
例如：二进制乘法：0111x0011=0-7x1+7x4=0-7+28=21
若 $[x]_{补} = x_{n - 1} x_{n - 2} ... x_{1} x_{0}$ ，则 $x = - 2^{n - 1} x_{n - 1} + i = 0 \sum n - 2 x_{i} 2^{i}$
若 $[y]_{补} = y_{n - 1} y_{n - 2} ... y_{1} y_{0}$ ，则 $y = - 2^{n - 1} y_{n - 1} + i = 0 \sum n - 2 y_{i} 2^{i}$

[x \times y]_{补} = [x]_{补} \times y = [x]_{补} \times (- 2^{n - 1} y_{n - 1} + i = 0 \sum n - 2 y_{i} 2^{i}) = [x]_{补} \times [2^{n - 1} (y_{n - 2} - y_{n - 1}) + 2^{n - 2} (y_{n - 3} - y_{n - 2}) + ... + 2^{0} (y_{- 1} - y_{0})] = [x]_{补} \times i = 0 \sum n - 1 2^{i} (y_{i - 1} - y_{i}), 其中 y_{- 1} = 0

补码运算规则：

根据乘数相邻两位的不同组合，确定是 +[x]补 或 -[x]补
用Ｙ的值乘 [x]补，达到 [x]补 乘 [y]补,求出 [x*y]补，不必区分符号与数值位。
乘数最低一位之后要补初值为 0 的一位附加线路，并且每次乘运算需要看附加位和最低位两位取值的不同情况，决定如何计算部分积，其规则是：
- ００：＋０
- ０１：＋被乘数
- １０：－被乘数
- １１：＋０

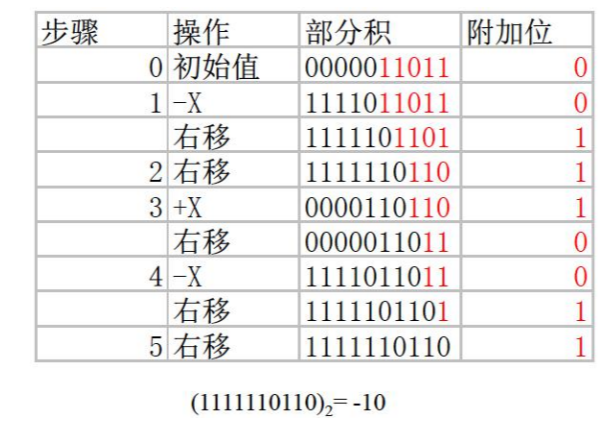
2x(-5) 示例：

乘法运算：小结

与加法比较，需要使用更多的硬件来实现，也更复杂
若使用简单的方法来实现，则需要多个计算周期
仅仅介绍了乘法运算的一些“皮毛” ：有许多提升和优化的空间

除法运算

在计算机内实现除运算时，存在与乘法运算类似的几个问题：

加法器与寄存器的配合，
被除数位数更长，
商要一位一位地计算出来等。这可以用左移余数得到解决，且被除数的低位部分可以与最终的商合用同一个寄存器，余数与上商同时左移。

除法可以用原码或补码计算，都比较方便，也有一次求多位商的快速除法方案，还可以用快速乘法器完成快速除法运算。

🌰Senjl's Digital Garden🐉

Explorer