2014-mid

判断

1. 即便 $f(n)=O(g(n))$，也未必有 $2^{f(n)}=O(2^{g(n)})$

❌

2. 不存在 CBA 式算法，能够经过少于 2n-3 次比较操作，从 n 个整数中找出最大和次大者。

✅ 最好情况，第一个和第二个整数正好是最大和次大，那么比较次数的下界为 n-1+n-2=2n-3

❌ 习题 2-40：2-40 CBA 找出最大者、次大者 最坏情况下不超过 $\lceil \frac{3n}{2}\rceil -2$ .思路是分治地查找

3. 存在 CBA 式算法，能够在 $O(n)$ 时间内从 n 个无序整数中找出最大的 10%

❌ 正确答案：✅ 先使用快速划分，在 $O(n)$ 的时间内找到第 10%大的元素，之后再遍历一遍，比这个元素大的就输出，小的就保留。

4. 起泡排序过程中，每经过一趟扫描交换，相邻的逆序对必然减少。

❌ 可能不变，如：2 3 1 4

5. 即便借助二分查找确定每个元素的插入位置，向量的插入排序最坏情况下仍需 $\Omega (n^2)$ 的时间

✅

6. 带权重的最优 PFC 编码树不仅未必唯一、拓扑结构未必相同，甚至树高也可能不等。

✅

多重选择

1. 若每一递归实例本身仅需常数时间和空间，则（ A, B ）函数的渐进时间复杂度等于渐进空间复杂度 A. 尾递归 B. 线性递归 C. 二分递归 D. 多分支递归

二分递归的经典实例：递归计算 fibonacci，其空间复杂度为递归深度 O (n)，但是时间复杂度 O (2^n) 多分支递归的经典实例：递归多路归并，空间复杂度也是递归深度 $O({\log }_{d}n)$，但是时间复杂度O（n）

2. 使用二分查找 C 版本在有序向量 {1,3,5,7,…, 2013} 中查找，目标为独立均匀分布于{0,2014} 内的整数。若平均失败查找长度为 F，则平均成功查找长度 S 应为（ B ） A. $\frac{1008F}{1007}+1$ B. $\frac{1008F}{1007}-1$ C. $\frac{1008(F-1)}{1007}+1$ D. $\frac{1008(F+1)}{1007}-1$

习题 2-18 ：2-18 binSearch 查找长度分析 这个结论适用于二分查找 A、B、C 和 FibSearch。

3. 设图灵机在初始状态下，只有读写头所对单元格为 '0'，其余均为 '#'；此后连续地执行 increase ()算法 2014 次，在此期间读写头累计移动的次数（就相对误差率而言）最接近于（ B ） A. 2000 B. 4000 C. 8000 D. 16000 E. 32000

$T(n)=2T(n-1)+2(n-1)$，其中 $n={\log }_{2}N$，N 为 increase 的次数 解出递推得：$T(n)=\sum _{i=1}^{n-1}{2}^i(n-i)$ ，代入 $n={\log }_{2}2014\approx 11$，解得累计移动次数约为 3982

答案：8000。 图灵机每次 increase 读写头移动次数=2 * (末尾连续的 1 的个数 +1 ) 但是我觉得此说法存疑。

4. 字符串 "123XY" 在经栈混洗后，可以得到（ 5 ）个合法的 C++变量名

变量名要求首字符为字母。

5. evaluate ()算法的优先级表中，有的空格项对应于表达式不合法或不合常识的情况，比如（ A, B, C, D ） A. pri['\0'][')'] B. pri['!']['('] C. pri[')']['!'] D. pri['(']['\0']

看优先级表即可。

6. 实际上，evaluate ()居然可以对非法表达式 (12)3+!4*+5 进行“求值”，其返回值为（ 89 ）

习题 4-12：4-12 evaluate ()对异常输入求值

7. 若仅考查最好情况下的渐进复杂度，则 Bubblesort（p163 版）、Insertionsort、Mergesort（p168+170 版）、Selectionsort 的非降排列次序是（ ）

各自最好情况和时间复杂度分别是：

• 已经有序，则 $\Theta (n)$
• 已经有序且是列表的形式，则 $\Theta (n)$，否则都严格大于这个复杂度
• 无论如何，都要 $\Omega (n\log n)$
• 列表，则 $O(n^2)$，无论如何都要查找完 unsorted 区间才能确定最大值；

所以排序是 B<I<M<S

8. （ C, D ）算法在最好情况与最坏情况下的渐进性能相同。 A. Bubblesort（p163 版） B. Insertionsort C. Mergesort（p168+170 版） D. Selectionsort

各自最坏情况和时间复杂度：

• 完全倒序，则 $O(n^2)$
• 完全倒序且是向量，则 $O(n^2)$
• $\Omega (n\log n)$
• 无论如何，每轮选数总要扫描一遍 unsorted 区间，则 $O(n^2)$

9. 将有序列表 L 均分成长为 $\Theta (h)$ 的 k 段，各段分别置乱，则 L.insertionSort() 至多只需要（ C ）的时间。 A. $\Theta (h^2\cdot k^2)$ B. $\Theta (h\cdot k^2)$ C. $\Theta (h^2\cdot k)$ D. $\Theta (h\cdot k)$

10. 若将有根有序的多叉树 T 所对应的二叉树记作 B (T)，则 T 的（ B, D ）遍历序列和 B (T)的（ ）遍历序列完全相同。 A. 后序 … 后序 B. 后序 … 中序 C. 层次 … 先序 D. 先序 … 先序 E. 以上皆非

这里 B 要注意理解，虽然很难表述原因，但确实涉及到后序遍历和中序遍历的本质。

11. 在二叉树（ A, D ）的遍历序列中，祖先节点一定位于后代节点之前。 A. 先序 B. 中序 C. 后序 D. 层次 E. 以上皆非

12. Huffman 算法中，若每次字符合并时均保证左兄弟不小于右兄弟，则在所生成编码树的层次遍历序列中，（ C ）必然按其频率的非升次序排列。 A. （仅）叶节点 B. （仅）内部节点 C. 所有节点 D. 以上皆非

填空

1. 表达式 (0!+1)*2^(3!+4)-5/(6!/7!)-8+9 所对应的 RPN 式为：

0! 1 + 2 3! 4 + ^ * 5 6! 7! / / - 8 - 9 +

2. 对由 2014 个节点构成的完全二叉树做层次遍历，辅助队列的容量至少为（ 1007 ）；在整个遍历过程中，辅助队列的规模共在（ 1006,1007 ）步迭代中处于这一规模。

3. 对 2 亿余元，均为百元面额真币，按编号手工排序，若只用基本的冒泡排序算法，则即使每秒完成一次比较和交换，亦大致耗时（ 1300 ）世纪。

$O(n^2)\approx (2\times 10^6{)}^{2}sec\approx 1.3\times 10^3\text{centuries}$

4. 设在 List::selectionSort() 算法中，将 insertB(tail,remove(selectMax(head->succ,n))); 替换为 swap(tail->pred->data,selectMax(head->succ,n)->data); 。若输入列表为{1962,1963,…, 2014; 1,2,3,…, 1960,1961}，则 swap()语句无实质效果（原地交换）的情况共出现（ 52 ）次

习题 3-14：3-14 循环节的应用 循环节是公差为 53 的等差序列，共有 53 个循环节，每个循环节长度为 2014/53=38

计算

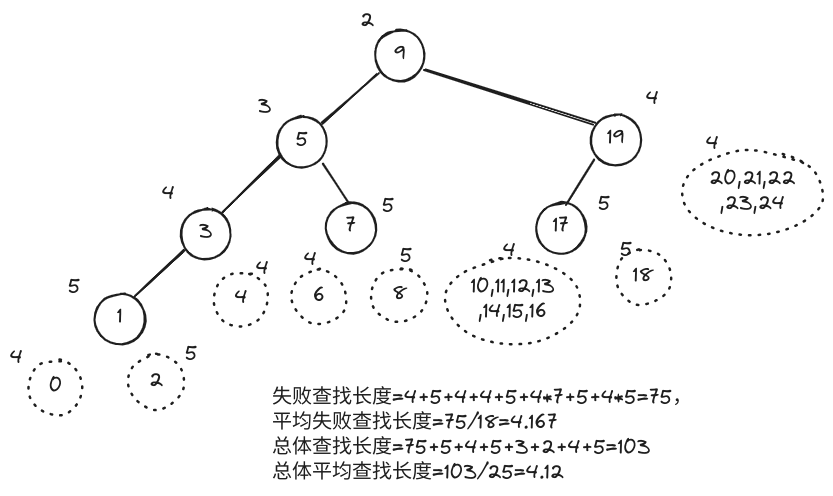
设整数 e 独立且均匀地取自 [0,25)，则通过 fibSearch(A,e,0,7)，对如下整型向量 A[] 做查找：

k      0   1   2   3   4   5   6
A[k]   1   3   5   7   9  17  19

则分别计算在失败情况下的平均查找长度，以及总体的平均查找长度。

fibSearch 的查找树：

证明

在由 n 个节点构成的二叉树中，任意节点 $v_i$ 和 $v_j$ 之间的距离取作二者之间唯一通路的长度，记作 $||v_i{v}_j||$ 。试证明：若二叉树的先序遍历序列为 $\{v_0,v_1,v_2,...,v_{n-1}\}$，则有：$\sum _{k=0}^{n-1}||v_k{v}_{k+1}\mathrm{mod}n||=||v_0{v}_1||+||v_1{v}_2||+...+||v_{n-2}{v}_{n-1}||+||v_{n-1}{v}_0||=2(n-1)$

n-1 是二叉树的边的数量，而先序遍历过程恰好每条边都经过了两遍。

算法

以下代码中的 int parent[0,n) 是采用父节点表示法存储的任意一棵有根的多叉树（未必有序）。

int f(int parent[], int n){ // -1<n
	
	
	int h=-1;


	for(int i=0;i<n;i++)

		h = __max(h,g(parent,i));

	return h;
}

int g(int parent[], int i){

	if (-1 == i) return -1;

	return 1+g(parent,parent[i]);
}

1. 以上算法中 f() 和 g() 分别是何功能？

f() 是找到全树的最大高度 g() 是某一个节点到根的距离

2. 最坏情况下，算法 f() 的渐进时间复杂度是多少？最坏情况何时出现？

最坏情况就是每个节点都要与其它所有节点比较、找到最大值，因此这种情况就是单链的树，时间复杂度是 $O(n^2)$

3. 不做任何删除的前提下，试通过增加尽可能少的代码，使 f() 的运行时间降低至 O(n)，空间不超过 O(n)。简要说明改进策略和思路，直接在原代码基础上完成修改，作为关键环节增加注释。

记忆化搜索，打个表。