B1-Sort-Exercise

12-1 构造轴点的 LGU 策略

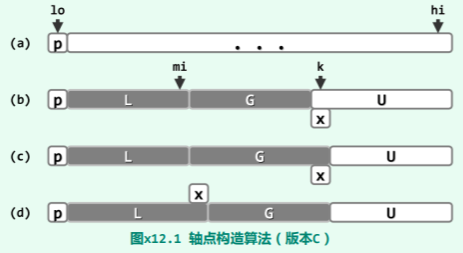说明：思路如上图。始终将整个向量 V[lo, hi] 划分为四个区间：

• V[lo]，
• L = V(lo, mi]，
• G = V(mi, k)，
• U = V[k, hi] 其中 V[lo] 为候选轴点，L/G 中的元素均不大/不小于 V[lo]，U 中元素的大小未知。 初始时取 k - 1 = mi = lo，L 和 G 均为空；此后随着 k 不断递增，逐一检查元素 V[k]，并根据 V[k] 相对于候选轴点的大小，相应地扩展区间 L（图(d)）或区间 G（图(c)），同时压缩区间 U。 最终当 k - 1 = hi 时，U 不含任何元素，于是只需将候选轴点放至 V[mi]，即成为真正的轴点。

1. 代码实现这个策略。 轴点划分：LGU 版

2. LGU 版的快速排序是否稳定？ 不稳定。按照以上算法划分向量的过程中，子向量 L 和 G 都是向右侧“延伸”，新元素都是插至各自的末尾。除此之外，子向量 L 不会有任何修改，故其中所有元素之间的相对次序，必然与原向量完全一致。然而，在子向量 L 的每次生长之前，子向量 G 都需要相应地向前“滚动”一个单元，故可能造成雷同元素之间相对次序的紊乱。

3. 基于 LGU 的快速排序，是否能高效处理大量元素重复的退化情况？ 在元素大量甚至完全重复的情况下，以上划分算法虽不致出错，但划分所得子向量的规模相差悬殊，快速排序算法几乎退化为起泡排序算法，整体运行时间将增加到 O(n^2)。

12-1-补 三点取中法的失衡概率

说明：快速排序算法选取轴点时可以采取不同的策略，本题试图用实例说明“三者取中”的策略比随机选取的策略倾向于得到更平衡的轴点，设待排序序列的长度 n 很大，若轴点的选取使得分割后长/短子序列的长度比大于9:1，则称为不平衡。针对不同的轴点选取策略，估计其发生不平衡的概率 (请填十进制小数)：

1. 从 n 个元素中等概率随机选取一个作为轴点： 不妨假设原数组 A[1..n] 的元素是互异的(不互异也可以在 O(n) 时间内添加扰动使之互异，但这不是该问题的关键)。则在 A 数组中任取一个元素的概率相等，均为 $\frac{1}{n}$，当元素取自 A[1,n/10] 和 A(9n/10,n] 两个区间时，显然不平衡。即发生概率为：$P=(\frac{n}{10}-1+1+n-\frac{9n}{10})/n=0.2$

2. 从 n 个元素中等概率选取三个元素，以它们的中间元素作为轴点： 使用 S[1..n] 表示对 A 数组排序后的结果。用三数取中法选择其中的中位数 $x$（后称主元），定义主元在 S[] 中的位置 i 的概率为 $p_i=Pr(x=S[i])$ ，显然 $i=2,3,4,...,n-1$。

则考虑用 n 和 i 表示的概率表达式：

• 从 n 个元素中任取三个元素，可能的组合数有 $C_n^3=\left(\genfrac{}{}{0ex}{}{n}{3}\right)=\frac{n(n-1)(n-2)}{6}$ 种
• 而这三个元素构成一个子集 S'[] ，其排序一共可能有 $A_3^3=6$ 种，其中第二个元素 S'[2]=S[i] 的概率就是要求的概率表达式。此时，子集 S' 的第一个元素取自 S[1..i-1] 中，共 i-1 种可能，第三个元素取自 S[i+1..n] 中，共 n-i 种可能
• 故综上，$p_i=\frac{6(n-i)(i-1)}{n(n-1)(n-2)}$

此时，一个平衡的划分，意味着 $\frac{n}{10}\le i\le \frac{9n}{10}$ ，则平衡的概率 $\sum _{i=\frac{n}{10}}^{\frac{9n}{10}}{p}_i\approx {\int }_{\frac{n}{10}}^{\frac{9n}{10}}\frac{6(n-i)(i-1)}{n(n-1)(n-2)}di=\frac{6\left(\frac{59}{375}{n}^3-\frac{6}{5}{n}^2\right)}{n(n-1)(n-2)}$ 当 $n\to \infty$ 时，上式趋近于 $\frac{354}{375}$，于是不平衡的概率 $=1-\frac{354}{375}=\frac{21}{375}=0.056$

12-2 考查众数候选算法

template <typename T> T majEleCandidate( Vector<T> A ) { //选出具备必要条件的众数候选者
   T maj; //众数候选者
// 线性扫描：借助计数器c，记录maj与其它元素的数量差额
   for ( Rank c = 0, i = 0; i < A.size(); i++ )
      if ( 0 == c ) { //每当c归零，都意味着此时的前缀P可以剪除
         maj = A[i]; c = 1; //众数候选者改为新的当前元素
      } else //否则
         maj == A[i] ? c++ : c--; //相应地更新差额计数器
   return maj; //至此，原向量的众数若存在，则只能是maj ―― 尽管反之不然
}

1. 分析：该候选者尽管不见得必然是众数，但是否必然是原向量中出现最频繁的元素？ 未必。该算法采用减而治之的策略，原向量被等效地切分为若干区段，各区段的首元素分别在其中占至少50%的比例（不妨称作“准众数”）。因此，最终返回的 maj，实际上只是最后一个区段的准众数，未必就是整个向量的（准）众数。

2. 该返回值在向量中出现的次数最少可能是多少？试举一例。 实际上，无论原向量的长度如何，只要其中的确不包含众数，则最终返回的 maj 都有可能仅出现一次。作为一个实例，我们考查如下长度为 n = 22的向量 A[]： { 0, 1; 0, 0, 1, 1; 0, 0, 0, 1, 1, 1; 0, 0, 0, 0, 1, 1, 1, 1; 2, 1 } 其中，元素0、1和2分别出现了10次、11次和1次。

若采用 majEleCandidate()算法，整个向量将等效于被分成5个区间：前4个区间 A[0, 2)、A[2, 6)、A[6, 12) 和 A[12, 20)，均以0作为 maj 候选；最后的 A[20, 22) 以2作为 maj 候选，并最终返回 2。显然，仅出现一次的元素2在这里既非频繁数，更非（准）众数。

12-3 众数定义改为“不少于一半”的分析

1. 该节设计的算法框架是否可以沿用？或需如何调整？ 算法框架 可以继续沿用。 请注意，在目前的总体框架 majority() 中，最终一步都会调用 majEleCheck()，通过对原向量一趟遍历，针对候选者做严格的甄别。

因此，只要 majEleCandidate()算法能在此之前筛选出唯一的候选者，就不致误判或漏判。

2. ==majEleCandidate() 算法是否可以沿用？或需如何调整？== 如此放宽众数的标准之后，我们需要计算的，实际上就是 习题12-2-1）所定义的准众数。 但若继续沿用目前的 majEleCandidate() 算法，则有可能造成漏判。 继续考查 习题12-2-2 所给的实例，可以看到一个有趣的现象：其中的元素1明明是准众数（在所有 n = 22个元素中，它恰好出现了 n/2 = 11次），但却未被任何一个区间选作 maj。 这就意味着，majEleCandidate() 算法注定无法将该元素作为 maj 返回，从而造成遗漏。

显然，当向量规模 n 为奇数时，准众数必然就是众数，因此不妨只考查 n 为偶数的情况（如上例）。此时针对准众数的查找，对原众数查找算法的一种简明调整方法是：首先任选一个元素 （比如末元素），并在 O(n)时间内甄别其是否为准众数。不妨设该元素不是准众数，于是只需将其忽略（原向量的有效长度减至奇数 n - 1），即可将在原向量中查找准众数的问题，转化为在这个长度为 n - 1的向量中查找众数的问题。

12-5 蛮力查找中位数算法的改进

// 中位数算法蛮力版：效率低，仅适用于max(n1, n2)较小的情况
template <typename T> //子向量S1[lo1, lo1 + n1)和S2[lo2, lo2 + n2)分别有序，数据项可能重复
T trivialMedian( Vector<T>& S1, Rank lo1, Rank n1, Vector<T>& S2, Rank lo2, Rank n2 ) {
   Rank hi1 = lo1 + n1, hi2 = lo2 + n2;
   Vector<T> S; //将两个有序子向量归并为一个有序向量
   while ( ( lo1 < hi1 ) && ( lo2 < hi2 ) )
      S.insert( S1[lo1] <= S2[lo2] ? S1[lo1++] : S2[lo2++] );
   while ( lo1 < hi1 ) S.insert( S1[lo1++] );
   while ( lo2 < hi2 ) S.insert( S2[lo2++] ); 
   return S[( n1 + n2 ) / 2]; //直接返回归并向量的中位数
}

1. 这一算法实际迭代 (n1+n2)/2 步即可终止，试改进算法。 这里计算的目标，是归并之后向量中的中位数，然而这并不意味着一定要显式地完成归并。 实际上就此计算任务而言，只需设置一个计数器，而不必真地引入并维护一个向量结构。

具体地，依然可以沿用原算法的主体流程，向量 S 只是假想式地存在。于是，我们无需真地将子向量中的元素注意转移至 S 中，而是只需动态地记录这一假想向量的规模：每当有一个元素假想式地归入其中，则计数器相应地递增。一旦计数器抵达 $\lfloor \frac{n1+n2}{2}\rfloor$，即可忽略后续元素并立即返回假想向量的末元素——亦即，两个子向量当前元素之间的更小者。

2. 这样改进后算法的渐进复杂度是否有所降低？ 没有实质的降低。 改进后的算法仍需迭代 $\lfloor \frac{n1+n2}{2}\rfloor$ 步，总体的渐进时间复杂度依然是 $O(n1+n2)$。

12-7 不等长向量长度的 median() 算法分析

//任意长度的子向量
template <typename T> //向量S1[lo1, lo1 + n1)和S2[lo2, lo2 + n2)分别有序，数据项可能重复
T median ( Vector<T>& S1, Rank lo1, Rank n1, Vector<T>& S2, Rank lo2, Rank n2 ) { //中位数算法
   if ( n1 > n2 ) return median( S2, lo2, n2, S1, lo1, n1 ); //确保n1 <= n2
   if ( n2 < 6 ) //递归基：1 <= n1 <= n2 <= 5
      return trivialMedian( S1, lo1, n1, S2, lo2, n2 );
   //////////////////////////////////////////////////
   //                 lo1     lo1 + n1/2  lo1 + n1 - 1
   //                 |       |           |
   //                 X >>>>> X >>>>>>>>> X
   // Y .. trimmed .. Y >>>>> Y >>>>>>>>> Y .. trimmed .. Y
   // |               |       |           |               |
   // lo2   lo2+(n2-n1)/2  lo2+n2/2 lo2+(n2+n1)/2  lo2+n2-1
   //////////////////////////////////////////////////
   
   if ( 2 * n1 < n2 ) //若两个向量的长度相差悬殊，则长者（S2）的两翼可直接截除
      return median( S1, lo1, n1, S2, lo2 + ( n2 - n1 - 1 ) / 2, n1 + 2 - ( n2 - n1 ) % 2 );
   //////////////////////////////////////////////////
   //    lo1            lo1 + n1/2          lo1 + n1 - 1
   //     |                 |                       |
   //     X >>>>>>>>>>>>>>> X >>>>>>>>>>>>>>>>>>>>> X
   //                       |
   //                       m1
   //////////////////////////////////////////////////
   //                      mi2b
   //                       |
   // lo2 + n2 - 1    lo2 + n2 - 1 - n1/2
   //     |                 |
   //     Y <<<<<<<<<<<<<<< Y ...
   //                          .
   //                         .
   //                        .
   //                       .
   //                      .
   //                     .
   //                    .
   //                   ... Y <<<<<<<<<<<<<<< Y
   //                       |                 |
   //                       lo2 + (n1-1)/2    lo2
   //                       |
   //                       mi2a
   ///////////////////////////////////////////////////
   
   Rank mi1 = lo1 + n1 / 2;
   Rank mi2a = lo2 + ( n1 - 1 ) / 2;
   Rank mi2b = lo2 + n2 - 1 - n1 / 2;
   if ( S1[mi1] > S2[mi2b] ) //取S1左半、S2右半
      return median( S1, lo1, n1 / 2 + 1, S2, mi2a, n2 - ( n1 - 1 ) / 2 );
   else if ( S1[mi1] < S2[mi2a] ) //取S1右半、S2左半
      return median( S1, mi1, ( n1 + 1 ) / 2, S2, lo2, n2 - n1 / 2 );
   else //S1保留，S2左右同时缩短
      return median( S1, lo1, n1, S2, mi2a, n2 - ( n1 - 1 ) / 2 * 2 );
} //O(log(min(n1,n2))) ，可见实际上等长版本才是难度最大的

1. 分析算法并证明正确性。 该算法首先比较 n1和 n2的大小，并在必要时交换两个向量，从而保证有 n1 ⇐ n2。 以下，若两个向量的长度相差悬殊，则可对称地适当截除长者（S2）的两翼，以保证有： n1 ⇐ n2 ⇐ 2∙n1 因为 S2 两翼截除的长度相等，所以此后 $S1\cup S2$ 的中位数，依然是原先 $S1\cup S2$ 的中位数。

2. 证明该算法的精确上界为 O(log(min(n1,n2)))。 由以上分析可见，无论是交换两个向量，还是截短 S2，都只需常数时间。因此实质的计算， 只是针对长度均同阶于 min(n1, n2)的一对向量计算中位数。

与教材中对这一减而治之策略的分析同理，此后每做一次比较，即可将问题的规模缩减大致一半。因此，问题的规模将以1/2为比例按几何级数的速度递减，直至平凡的递归基。整个算法 的递归深度不超过 ${\log }_2(\min (n1,n2))$，总体时间复杂度为 $O(\log (\min (n1,n2)))$。

12-8 若输入序列 S1 和 S2 以列表形式则 median() 算法需作何调整？

1. ==两个 median() 的调整方向是==？ 这里的关键在于，列表仅支持“循位置访问”的方式，不能像“循秩访问”那样在常数时间内访问任一元素。特别地，在读取每个元素之前，都要沿着列表进行计数查找。

2. 调整之后计算效率如何？ 为保证|S1| ⇐ |S2|而交换两个序列（的名称），依然只需 O(1)时间；然而，序列 S2两翼的截短则大致需要 O(n2 - n1)时间。 而更重要的是，在此后的递归过程中，每一次为将问题规模缩减一半，都必须花费线性的时间。 因此，总体需要 O(n1 + n2)时间——这一效率，已经降低到与蛮力算法 trivialMedian 相同。

12-9 若输入序列以 BBST 方式给出，median() 如何调整？

为此，需要给平衡二叉搜索树增加以下接口：

• template BinNodePosi(T) & BBST::search(Rank r); //查找并返回树中第 r 大的节点
• template BinNodePosi(T) & BBST::removeMin(int k); //从树中删除最小的 k 个节点
• template BinNodePosi(T) & BBST::removeMax(int k); //从树中删除最大的 k 个节点

调整之后计算效率如何？ 仿照 quickSelect()算法，不难实现一个效率为 O(logn)的 search(r)接口。然而，高效的 removeMin(k)和 removeMax(k)接口并不容易实现。

实际上，一种简明的策略是：首先通过中序遍历，将平衡二叉搜索树中的所有元素转化为有序向量，然后套用以上算法计算中位数。 当然，按照这一策略，运行时间主要消耗于遍历，整体为 O(n1 + n2)——蛮力算法 trivialMedian()相同。

12-10 基于 median() 算法设计 k-selection 算法

记 n1 = |S1|和 n2 = |S2|，不失一般性，设 n1 ⇐ n2。 进一步地，不妨设2k ⇐ n1 + n2——否则，可以颠倒比较器的方向，原问题即转化为在 $S1\cup S2$ 中选取第 n1 + n2 - k 个元素，与以下方法同理。

若 k ⇐ n1 = min(n1, n2)，则只需令： S1' = S1[0, k) S2' = S2[0, k) 于是原问题即转换为计算 $S{1}^{\prime }\cup S{2}^{\prime }$ 的中位数。 否则，若 n1 < k < n2，则可令 S1' = S1[0, n1) S2' = S2[0, 2k - n1) 于是原问题即转换为计算 $S1\cup S{2}^{\prime }$ 的中位数。

可见，无论如何，针对 $S1\cup S2$ 的 k-选取问题总是可以在常数时间内，转换为中位数问题，并进而直接调用相应的算法。

由上可见，无论如何，都可在 O(1) 时间内将原问题转换为中位数的计算问题。借助 median() 算法，如此只需要 O(log(min(n1, n2))) 时间。

12-11 考查 quickSelect() 算法

Transclude of B0-Sort#^539dfb

1. 举例说明，该算法的外循环最坏情况下需要执行 Ω(n) 次。 在最坏情况下，每一次随机选取的候选轴点 pivot = A[lo] 都不是查找的目标，而且偏巧就是当前的最小者或最大者。于是，对向量的每一次划分都将极不均匀，其中的左侧或右侧子向量长度为0。

如此，每个元素都会被当做轴点的候选，并执行一趟划分，累计 Ω(n) 次。从算法策略的角度来看，原拟定的“分而治之”策略未能落实，实际效果反而等同于采用了 “减而治之”策略。

2. 在各元素独立等概率分布的条件下，该算法的平均时间复杂度是多少？ 仿照教材12.1.5节对 quickSort()算法的分析方法，同样可以证明，quickSelect()算法 的平均运行时间为 O(n)——在平均意义上，与 LinearSelect 相当。LinearSelect

12-12 基数排序推广：希尔排序的基本思想

基数排序思想

问题说明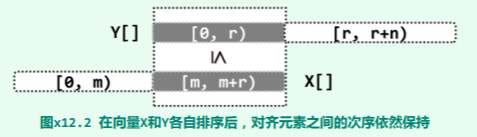： 如图所示，有向量 X[0,m+r) 和 Y[0,r+n)，且满足：对于任何 0⇐j<r，都有 Y[j]<=X[m+j]。试证明，在 X 和 Y 分别按非降次序排序后，对于任何 0⇐j<r 依然有 Y'[j]<=X'[m+j] 成立。实例如下：

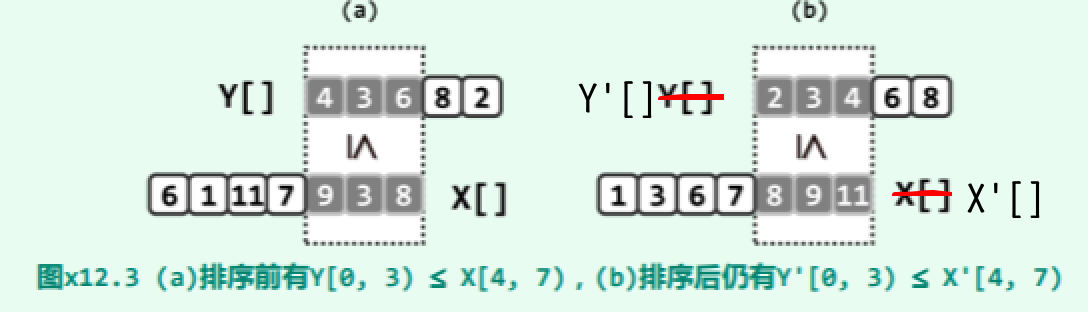
对于任意的0 ⇐ j < r，考查元素 X'[m + j] 。 一方面，在有序的 X’（以及无序的 X）中，显然应该恰有 m + j 个元素不大于 X'[m + j]。 而另一方面，由图 x12.2可见，其中至少存在 j 个元素，各自不小于无序的 Y（以及有序的 Y’） 中的某一元素，而且 Y（Y’）中的这些元素互不重复。也就是说，Y’（Y）中至少存在 j 个元素不大于 X'[m + j]，故必有： Y'[j] <= X'[m + j]

当然，仿照 习题2-41:基数排序思想 的两种证明方法，亦可得出同样结论。

12-13 证明 g-sorted 的向量经过 h-sorting 后亦然保持 g-sorted

在已经 h-sorting 之后的向量中，考查任一元素 A[i]，我们欲证总有 A[i] <= A[i + g]。如图 x12.4所示，考查 g-sorting 以及 h-sorting（在逻辑上）各自对应的二维矩阵。于是，在后一矩阵中，A[i + g] 必然落在深色阴影区域内部。我们继续在该矩阵中，考查 A[i] 以及 A[i + g] 各自所属的列。

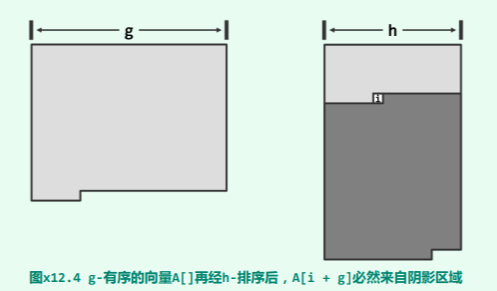
根据 g-有序性，如图 x12.5所示，两个列的前缀与后缀必然一一对应地有序，亦即： … A[i - 2h] <= A[i + g - 2h] A[i - h] <= A[i + g - h] A[i] <= A[i + g] A[i + h] <= A[i + g + h] A[i + 2h] <= A[i + g + 2h] …

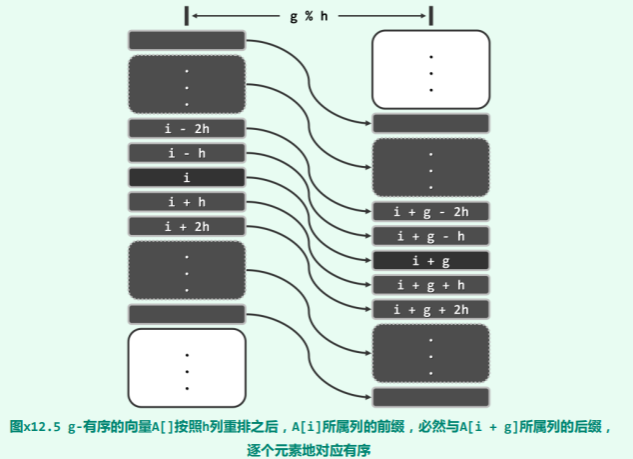
于是根据本章第 [12-12] 题的结论，在经过 h-排序之后，这两列的前缀和后缀之间的对应有序关系依然成立，g-有序性得以延续。

12-14 Pratt 序列分析

背景：使用 Pratt 序列：$H_{pratt}=\{1,2,3,4,6,8,9,12,16,...,2^p\cdot 3^q,...\}$ 对长度为 n 的任一向量 S 作希尔排序。试证明：

1. ==若 S 已经 (2,3)-sorted，则只需 O(n) 时间即可使之完全有序==。 根据教材第12.3.2节的分析结论，在(2, 3)-sorted 的序列中，逆序元素之间的间距不超过： (2 - 1) * (3 - 1) - 1 = 1 也就是说，整个向量中包含的逆序对不过 O(n)个。 于是根据 习题 3-11 的结论，此后对该向量的1-sorting 仅需 O(n)时间。

2. ==对任何 $h_k\in H_{pratt}$，若 S 已是 $(2h_k,3h_k)-sorted$，则只需 O(n) 时间即可使之 $h_k$ -sorted==. 既然所有元素的秩取值于 [0, n) 范围内，故若照相对于 $h_k$ 的模余值，它们可以划分为 $h_k$ 个 同余类；相应地，原整个向量可以“拆分为” $h_k$ 个接近等长的子向量。 不难看出，其中每个子向量都是(2, 3)-sorted 的，根据上一问的结论，均可在线性时间内转换为各自1-sorted 的；就其总体效果而言，等同于在 O(n)时间内转换为全局的 $h_k$ -sorted。

3. ==针对 $H_{pratt}$ 序列中的前 $O({\log }^{2}n)$ 项，希尔排序算法需要分别迭代一轮==。 $H_{pratt}$ 序列中的各项元素无非是 2^p 和 3^q 的乘积组合，因此其中不大于 n 项数最多不超过：${\log }_{2}n\times {\log }_{3}n=O({\log }^{2}n)$。

4. 总体的时间复杂度为 $O(n{\log }^{2}n)$. 综合 2）和 3）的结论，在采用 $H_{pratt}$ 序列的希尔排序过程中，每一轮耗时不超过 O(n)，累计至多迭代 $O({\log }^{2}n)$ 轮，因此，总体耗时不超过 $O(n{\log }^{2}n)$。