B0-Linear-Models-for-Classification

Linear Models for Binary Classification

回想之前学过的三种线性模型，它们的共同点是计算分数的 scoring function 都是线性的：$s={\mathbf{w}}^T\mathbf{x}$ ，最关键的差别就是对这个 score 的处理函数，并由此导致错误估计的不同：

• 
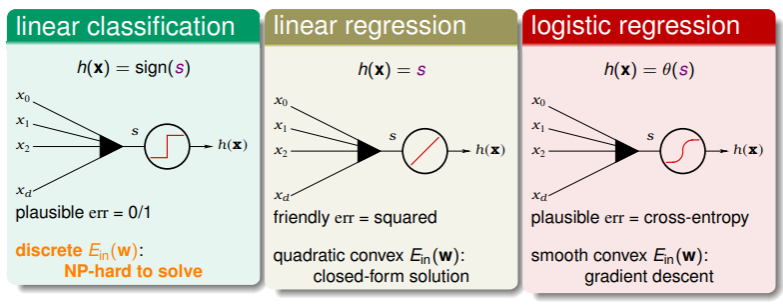
• 我们曾考虑使用 线性回归策略 缩短二元分类问题的迭代时间， Logistic Regression 的梯度下降策略也可以快速地找到最小的 $E_{in}(\mathbf{w})$ （至少比 NP-hard 复杂度高效得多），如何使用 Logistic Regression 优化二元分类问题呢？我们接下来就探讨这个。

Summary for Error Evaluating

来回顾一下这三个模型在二元分类问题上的错误评估函数：

• 
• 将三者用相同的参数统一表达，我们得到了上面的错误评估函数形式，其中 $ys$ 的物理意义是分类问题中分类正确的程度，其正负表明分类是否正确，其值越大则越正确；

将这三个函数可视化：

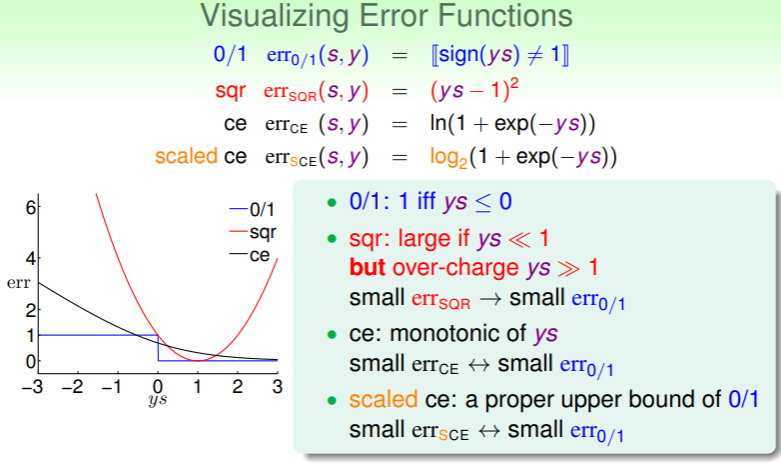• 可以总结出以下这些结论：
  • 当 $|ys|\to 1$ 时，线性回归的错误评估 ${\text{err}}_{SQR}$ 很小，但在 $|ys|\to \infty$ 时，反而增大（无论正负），回想之前说 ${\text{err}}_{SQR}$ 是 ${\text{err}}_{0/1}$ 的宽松上界，在 $|ys|$ 较大时尤为如此，在 $|ys|\to 1$ 时才勉强可以认为 ${\text{err}}_{0/1}\approx {\text{err}}_{SQR}$ ；
  • Logistic Regression 的错误评估 ${\text{err}}_{CE}$ 是一个单调递减的函数，不过根据图像可知，当 ${\text{err}}_{CE}$ 足够小时，也可以认为 ${\text{err}}_{CE}\approx {\text{err}}_{0/1}$ ；
  • 另外原始的 ${\text{err}}_{CE}$ 是 $\ln$ 形式的，它与 ${\text{err}}_{0/1}$ 有两个交点，我们换底成 ${\log }_2$ 形式，则转换成下图：

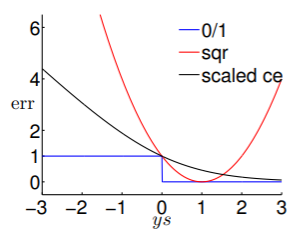
由此，我们再对错误评估函数做一些放缩：考虑到

$${\text{err}}_{0/1}(s,y)\le {\text{err}}_{SCE}(s,y)=\frac{1}{\ln 2}{\text{err}}_{CE}(s,y)$$

，可以认为在 $E_{in}$ 上满足

$$E_{in}^{\text{0/1}}(\mathbf{w})\le E_{in}^{\text{SCE}}(\mathbf{w})=\frac{1}{\ln 2}{E}_{in}^{\text{CE}}(\mathbf{w})$$

，从而在 $E_{out}$ 上满足

$$E_{out}^{\text{0/1}}(\mathbf{w})\le E_{out}^{\text{SCE}}(\mathbf{w})=\frac{1}{\ln 2}{E}_{out}^{\text{CE}}(\mathbf{w})$$

，因此回想之前 VC Dimension 中关于 $E_{in}$ 和 $E_{out}$ 的关系：

$$E_{out}^{\text{0/1}}(\mathbf{w})\le E_{in}^{\text{0/1}}(\mathbf{w})+{\Omega }^{\text{0/1}}$$

，我们可以放缩 $E_{out}^{\text{0/1}}$ 为：

$$\begin{array}{rl}{E}_{out}^{\text{0/1}}(\mathbf{w})& \le \frac{1}{\ln 2}{E}_{out}^{\text{CE}}(\mathbf{w})\\ & \le \frac{1}{\ln 2}{E}_{in}^{\text{CE}}(\mathbf{w})+\frac{1}{\ln 2}{\Omega }^{\text{CE}}\end{array}$$

，因此我们有理由相信，足够小的 $E_{in}^{\text{CE}}$ 也能够得到足够小的 $E_{out}^{\text{0/1}}$ 。

Regression for Classification

此时，无论线性回归还是 Logistic Regression，我们都论证了其用于二元分类问题的可行之处：

• 
• 综合起来，我们可以用线性回归找到较好的 ${\mathbf{w}}_0$ 作为起始，然后再运行 PLA/pocket/Logistic Regression 这些算法。

Stochastic Gradient Descent

我们学习了两种迭代式的优化方法，一种是 PLA 风格的，一种是 pocket 或 Logistic Regression 风格的，不过这两者在每轮迭代的时间复杂度相去甚远：

• 

Decrease the Iterative Complexity

如何将 Logistic Regression 的每轮复杂度也降低到 $\mathcal{O}(1)$ 呢？回想其迭代的公式：

$${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t-\eta \underset{-\nabla E_{in}({\mathbf{w}}_t)}{\underbrace{\frac{1}{N}\sum _{n=1}^N\theta (-y_n{\mathbf{w}}_t^T{\mathbf{x}}_n)(-y_n{\mathbf{x}}_n))}}$$

，我们想要更新方向是趋于单位长度的，这里经过连加后求平均的式子是 $\mathcal{O}(N)$ 的罪魁祸首。

因此为了优化复杂度，我们选择在 n 个输入中随机地挑选一个，那么在期望上是接近平均值的（类比：要求 1~999 的平均数，连加起来复杂度很高，而随机抽一个数，这个数在平均数 500 附近的概率就会服从均匀分布），这就是 stochastic gradient ：在随机的 $n$ 上做偏微分 ${\nabla }_{\mathbf{w}}\text{err}(\mathbf{w},{\mathbf{x}}_n,y_n)$ ，此时，真正的微分形式就变成：

$${\nabla }_{\mathbf{w}}{E}_{in}(\mathbf{w})=\underset{\text{random }n}{\mathbb{E}}{\nabla }_{\mathbf{w}}\text{err}(\mathbf{w},{\mathbf{x}}_n,y_n)$$

Understand SGD

如何理解 SGD？实际上，随机梯度可以看作是真实梯度和“噪音”的混合：

$$\mathrm{stochastic}\mathrm{gradient}=\mathrm{true}\mathrm{gradient}+\text{‘noise’ }\mathrm{directions}$$

，因此将真实梯度换作随机梯度，就是随机梯度下降。

• 经过足够轮次的迭代，我们可以期望地认为，$\mathrm{average}\mathrm{true}\mathrm{gradient}\approx \mathrm{average}\mathrm{stochastic}\mathrm{average}$ ；
• SGD 的优势是简单、高效，尤其是在大量数据和在线学习两种情况中；但是相应的，会导致运行过程不够稳定，因此只能通过增加迭代轮次来提高稳定结果的概率；

SGD 的迭代公式可以写作：

$${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t+\eta \underset{-\nabla \text{err}({\mathbf{w}}_t,{\mathbf{x}}_n,y_n)}{\underbrace{\theta (-y_n{\mathbf{w}}_t^T{\mathbf{x}}_n)(y_n{\mathbf{x}}_n))}}$$

，这看起来与 PLA 的迭代公式十分类似：

$${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t+1\cdot [y_n\ne \text{sign}({\mathbf{w}}_t^T{\mathbf{x}}_n)](y_n{\mathbf{x}}_n)$$

，实际上 SGD Logistic Regression 可以看作“soft”PLA ；或者在 $\eta =1$ 且当 ${\mathbf{w}}_t^T{\mathbf{x}}_n$ 足够大时，可以认为 $\mathrm{PLA}\approx \mathrm{SGD}$ ；

在使用 SGD 时有两点值得注意：

1. 何时停止？由于 SGD 的原理，我们不方便计算确切的梯度，因此考虑运行足够多轮次时就停止；
2. $\eta$ 取何值？经验上，$\eta =0.1$ 比较合适；

练习：应用 SGD 策略

• 从物理意义上讲，残差越大就更新越多，所谓残差就是 $y_n$ 与 ${\mathbf{w}}_t^T{\mathbf{x}}_n$ 的差值，代表着实际与预测的差距；

Multiclass via Logistic Regression

那么如何从之前学习过的模型应用到多分类问题呢？为了表述明确，我们称为 $k$ 分类问题：

首先考虑线性分类模型，对一个特定分类 $i$ 设定为 +1 ，剩余其它分类为 -1 ，迭代 $k$ 次即可得到：

• 
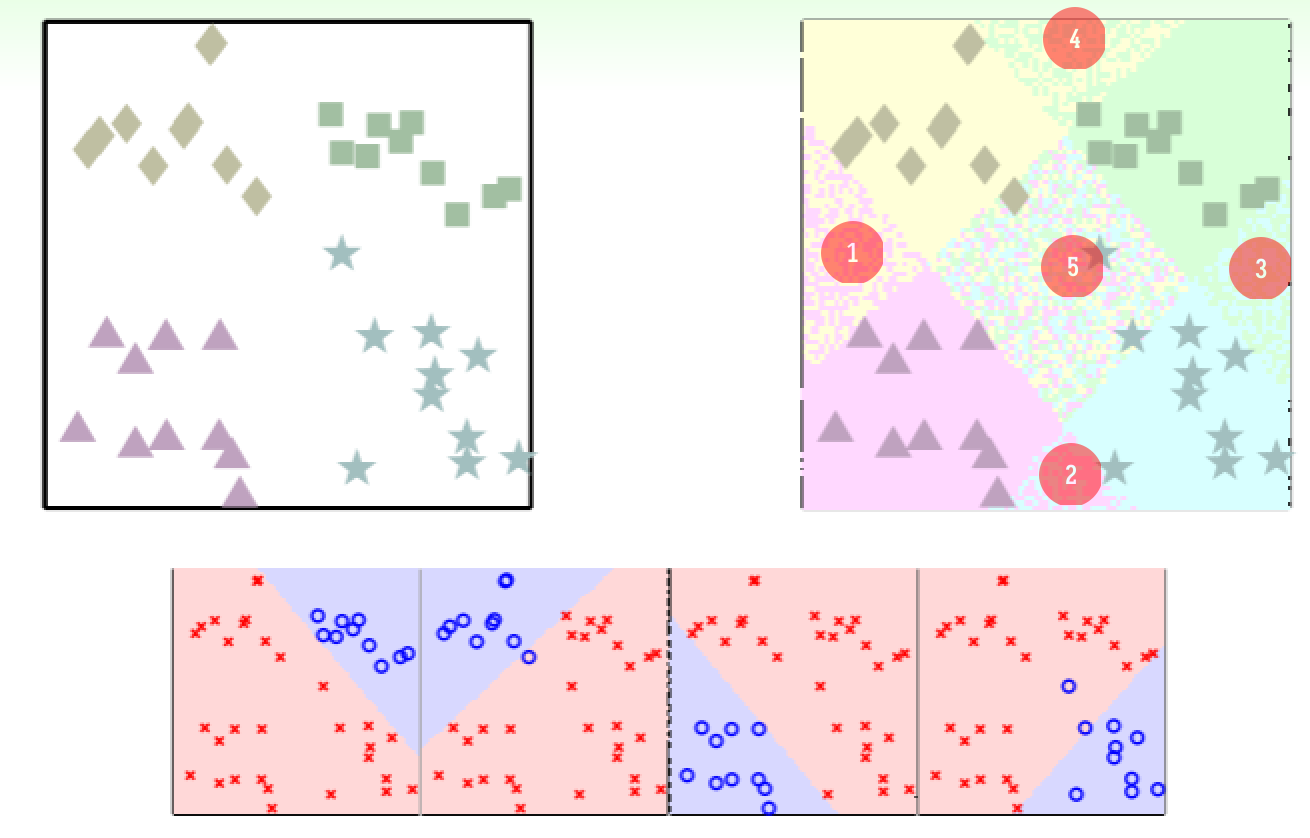
• 在每轮迭代时，都将目标分类的样本与其它样本剔除开来，这样得到的结果就实现了多分类。但是问题是，在聚集区域表现良好，但是在临界区域表现较差，上图中 1~5 这五个临界区要么发生争抢、要么被所有分类都拒绝。

于是考虑 Logistic Regression 这个软分类模型，依旧是每轮都对特定分类进行区分，迭代 $k$ 次，但区别在于每轮中给出的是样本属于特定分类的概率，根据概率的大小再进行分类：

• 
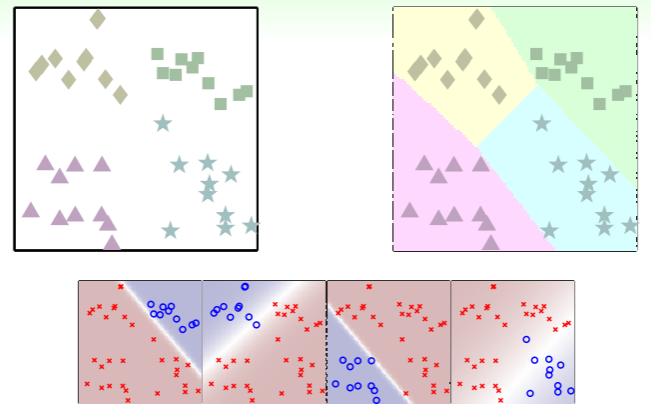
• 实现起来，就是每轮的分类器对所有样本作出属于该分类与否的概率 （于是得到 $k$ 个概率），然后选择其中最大概率作为该样本的分类：$g(\mathbf{x})=arg{\max }_{k\in \mathcal{Y}}\theta ({\mathbf{w}}_{[k]}^T\mathbf{x})$

One-Versus-All Decomposition

直观上看，使用 Logistic Regression 的准确率更高，对这种方法我们整理一下流程：

1. 每一轮在数据集上运行一次 Logistic Regression —— ${\mathcal{D}}_{[k]}=\{({\mathbf{x}}_n,y_n^{{}^{\prime }}=2[y_n=k]-1){\}}_{n=1}^N$，因此得到一个权重向量组 ${\mathbf{w}}_{[k]}$ ，
2. 对每一个样本，都返回权重向量组中计算得到的最大概率值：$g(\mathbf{x})=arg{\max }_{k\in \mathcal{Y}}\theta ({\mathbf{w}}_{[k]}^T\mathbf{x})$

这种策略的优势是高效准确、是组合应用 Logistic Regression 风格的方法实现的，但缺点是当分类数 $k$ 较大时，不够平衡，比如有 100 个分类，每轮分类器都简单的全部否认，那么准确率仍然有 99% ，这显然不合理。

之所以叫 One-Versus-All (OVA) ，就是因为分类的选取是从 $k$ 个里选一个。更高级的 OVA 扩展思路，可以看：multinomial logistic regression 。

练习：理解 OVA 的思路

Multiclass via Binary Classification

OVA 中最大的缺点是处理分类数 $k$ 较大时不够平衡的问题，要解决这个问题，可以采用一对一的比较策略：

• 每轮只对目标分类和任一其它分类做比较，而其余 $k-2$ 个分类都视作不存在：
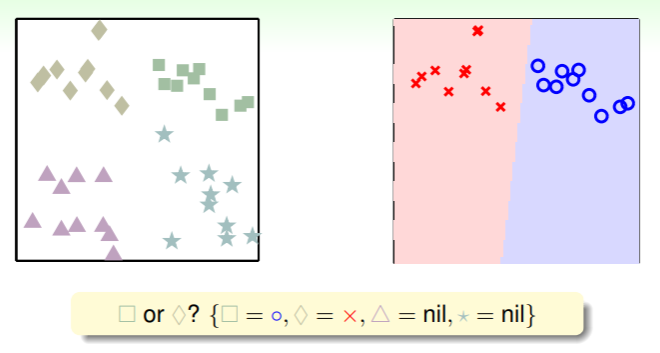
• 当 $k=4$ 时，则要经过六轮比较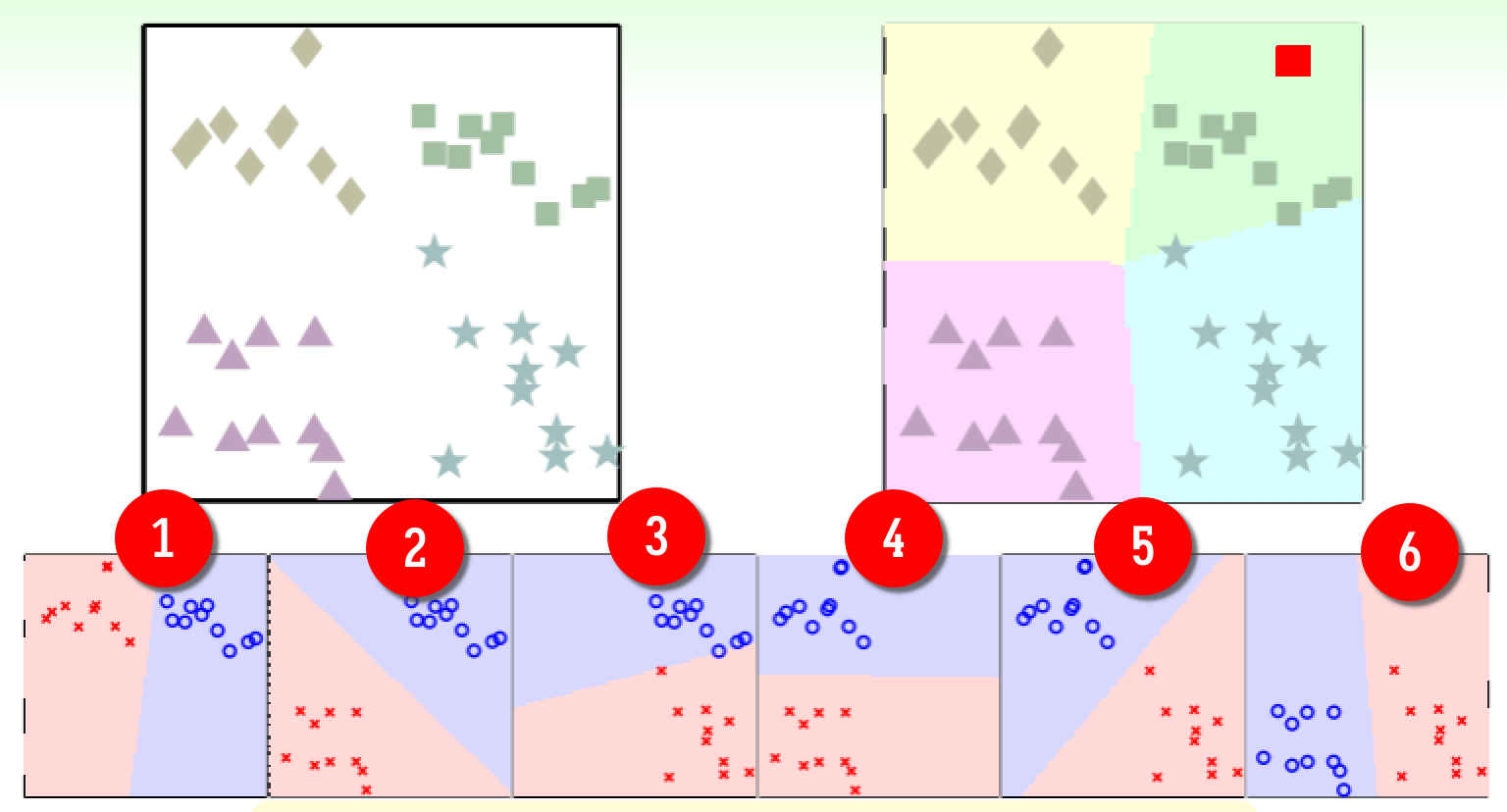： 通项公式是 $\text{compare times}=(k-1)+(k-2)+...+1=\frac{k(k-1)}{2}$ ；
• 那么经过六轮比较后，如何选取呢？类似锦标赛一样，得票数高者获胜：上图中对于样本（红色方块）六轮比较中 1、2、3 轮将其分类到方块类，4 轮分类到菱形类，5、6 轮分类到星形类，三角形类没有轮次分类到，即得票数 $3:1:2:0$ ，因此该样本是属于方块类的；

One-Versus-One Decomposition

综合上面的思路，我们整理一下 One-Versus-One (OVO) 策略的流程：

1. 每一轮分类，在数据集上运行线性分类算法：${\mathcal{D}}_{[k,\ell ]}=({\mathbf{x}}_n,y_n^{{}^{\prime }}=2[y_n=k]-1):y_n=k\text{ or }{y}_n=\ell$ ，这里 $k=\ell$，表示每个分类对其它分类 1v1 比较后的结果，则有 $(k,\ell )\in \mathcal{Y}\times \mathcal{Y}$ ，由此得到元素为权重向量的一个二维矩阵 ${\mathbf{w}}_{[k,\ell ]}$ ；
2. 考查二维矩阵中每一个票数，选择最大者：$g(\mathbf{x})=\text{tournament champion}\left\{{\mathbf{w}}_{[k,\ell ]}^T\mathbf{x}\right\}$ ；

显然，OVO 策略比 OVA 策略更加稳定，是组合应用二元线性分类方法实现的；缺点就是计算效率太低，要得到二维权重矩阵 ${\mathbf{w}}_{[k,\ell ]}$ ，需要耗时 $\mathcal{O}(k^2)$ 。

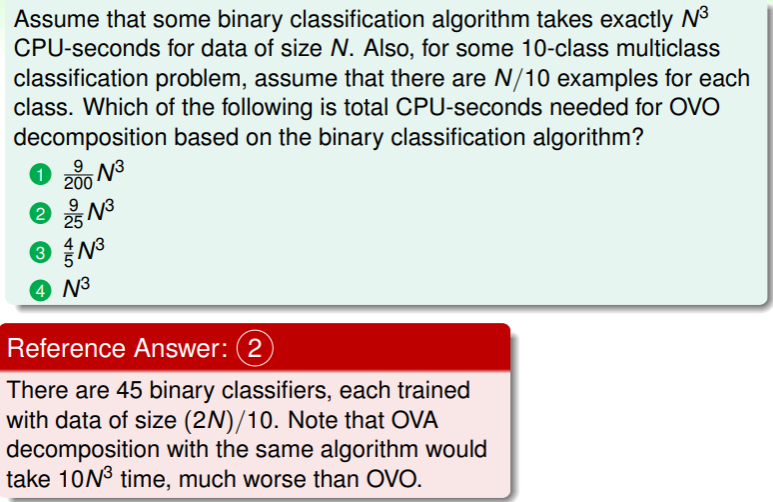
练习：计算 OVO 训练耗时

OVO 一定比 OVA 更耗时吗？

下题就表明 OVA 可能耗时比 OVO 更多。