61-Balanced-BST

AVL Tree

平衡因子

$ba lF a c (v) = h e i g h t (l c (v)) - h e i g h t (rc (v))$

高度与节点数

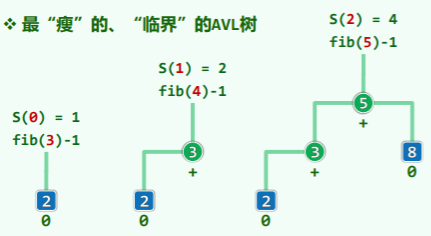
高度为 h 的 AVL 树，至少包含 $S (h) = f ib (h + 3) - 1$ 个节点。证明如下：

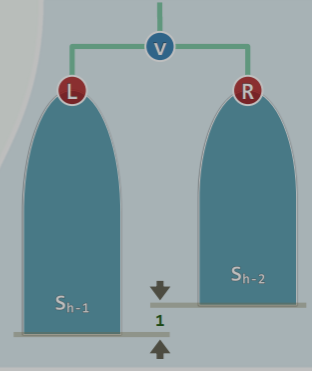
对给定高度 h 、节点数最少的 AVL 树，将其规模记作 S(h)，则有
$S (h) = 1 + S (h - 1) + S (h - 2)$
$S (h) + 1 = [S (h - 1) + 1] + [S (h - 2) + 1]$
$f ib (h + 3) = f ib (h + 2) + f ib (h + 1)$

反之同理，n 个节点构成的 AVL 树，高度不超过 O(logn)。

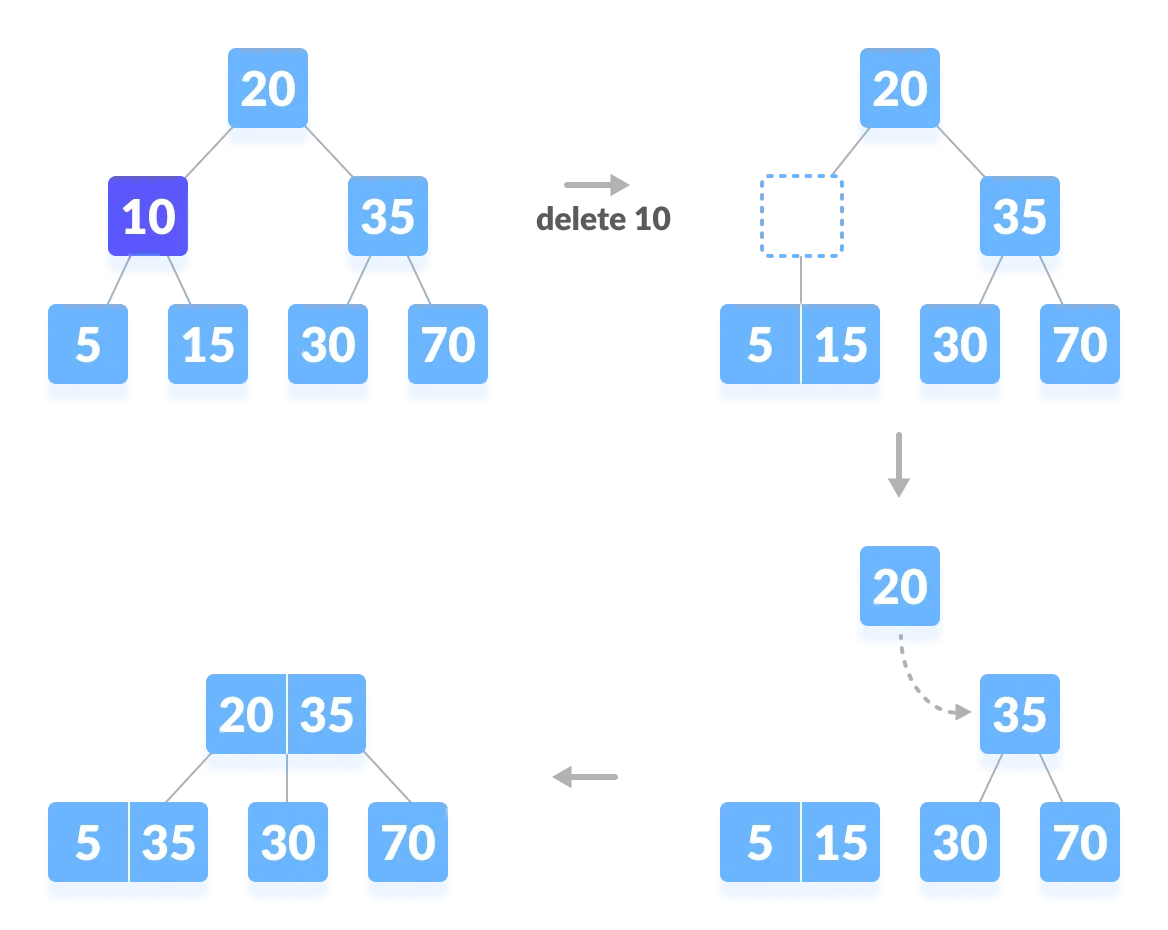
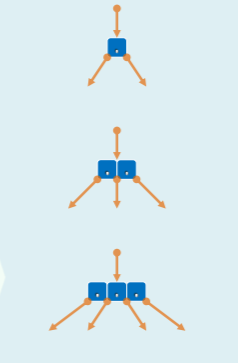
这种节点数最少的 AVL 树的形态是单侧高 1，且高的一侧仅一个节点：

失衡与复平衡

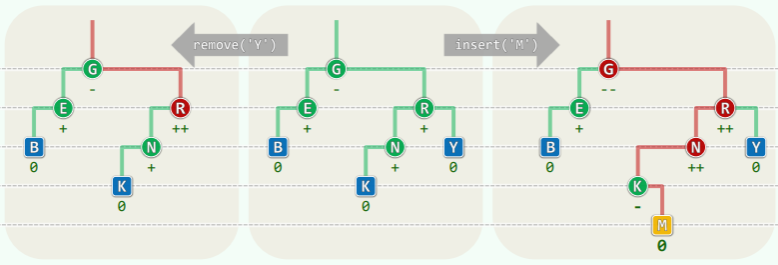
AVL 树在动态操作（插入、删除）后，可能会破坏平衡性，且该失衡只发生在被操作节点的祖先上：

插入：从祖父开始，每个祖先都有可能失衡，且可能同时失衡！
删除：从父亲开始，每个祖先都有可能失衡，但至多一个！（因为删除只会改变自己分支的高度，而不会影响另一个分支，因此只会影响到父亲的平衡因子）
虽然如此，看起来插入的影响较删除更大，但实际上插入造成的失衡恢复起来比删除简单得多。

// 涉及AVL树的平衡性的接口
#define Balanced(x) ( stature( (x).lc ) == stature( (x).rc ) ) //理想平衡

#define BalFac(x) (stature( (x).lc ) - stature( (x).rc ) ) //平衡因子

#define AvlBalanced(x) ( ( -2 < BalFac(x) ) && (BalFac(x) < 2 ) ) //AVL平衡条件

template <typename T> 
class AVL : public BST<T> { //由BST派生
public: //BST::search()等接口，可直接沿用
	BinNodePosi<T> insert( const T & ); //插入（重写）
	bool remove( const T & ); //删除（重写）
}

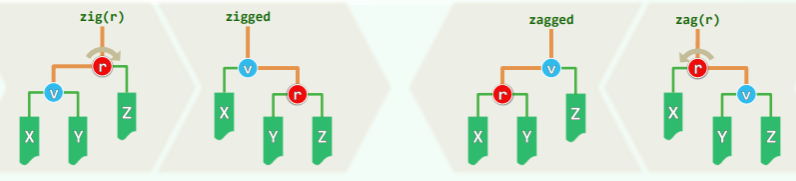
复衡的手段就是在局部进行旋转操作：

所有旋转都在局部进行，每次只需 O (1)时间；
每个深度只需检查并旋转至多一次，故总计 O (logn)次；

插入

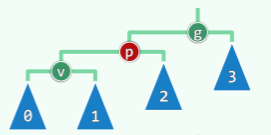
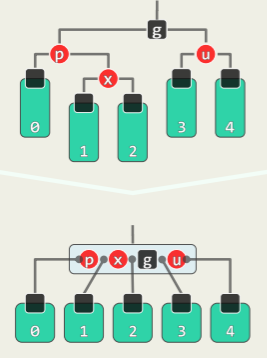
insert (x)可能造成同时有多个失衡的节点，其中失衡的最低者 g 不低于 x 的祖父。共有两种情况，分别通过一次旋转和两次旋转可以复衡：

单旋：x 在失衡局部的两侧
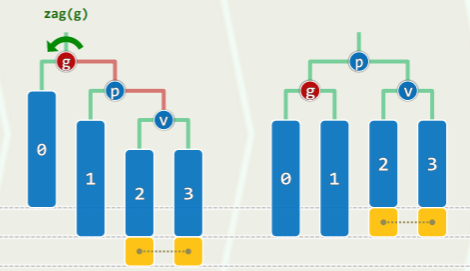
- 上图中 x 插入黄色方块中任意一处，镜像情况同理；
- g 只需经过单次旋转后就能复衡，g 作根节点的子树的高度复原（子树高度不变化）
- 更高祖先因此复衡，全树复衡；
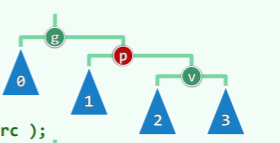
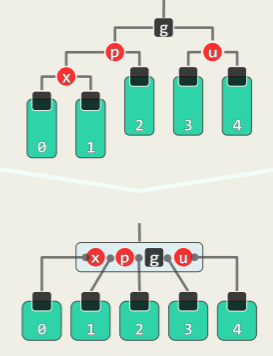
双旋：x 在失衡局部的中间
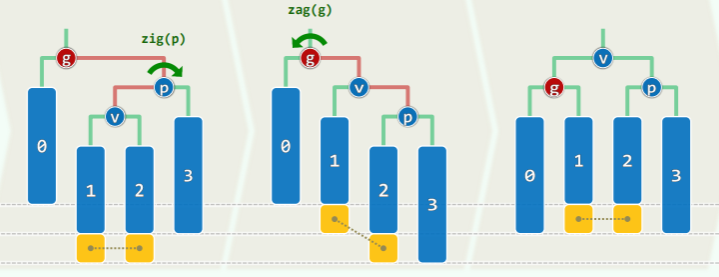
- 先对失衡节点 g 的孩子（x 插入的子树）进行一次旋转，然后对失衡节点 g 进行一次旋转；
- 同样，以 g 作根节点的子树的高度复原，更高祖先同时复衡；

template <typename T>
BinNodePosi<T> AVL<T>::insert( const T & e ) {
	BinNodePosi<T> & x = search( e ); 
	if ( x ) return x; //若目标尚不存在
	
	BinNodePosi<T> xx = x = new BinNode<T>( e, _hot ); _size++; //则创建新节点
	// 此时，若x的父亲_hot增高，则祖父有可能失衡
	for ( BinNodePosi<T> g = _hot; g; g = g->parent ) //从_hot起，逐层检查各代祖先g
	if ( ! AvlBalanced( *g ) ) { //一旦发现g失衡，则通过调整恢复平衡
		FromParentTo(*g) = rotateAt( tallerChild( tallerChild( g ) ) );
		break; //局部子树复衡后，高度必然复原；其祖先亦必如此，故调整结束
	} else //否则（g仍平衡）
	updateHeight( g ); //只需更新其高度（注意：即便g未失衡，高度亦可能增加）
	return xx; //返回新节点位置
}

AVL 树插入操作时，即使未失衡，高度也有可能增加（上图 0 处子树高度多 1 的情况，再在其它子树插入时会造成高度增加）

删除

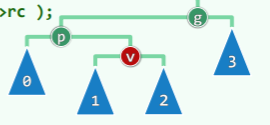
delete (x)操作可能造成至多一个失衡节点——失衡节点若出现，首个就是 x 的父亲_hot。要复平衡有两种情况：

单旋：导致失衡(黄色方块)的局部在两侧
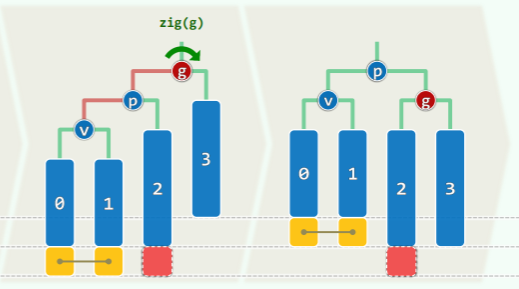
- 删除子树 3 的节点，而黄色节点任意存在一个，红色方块可有可无——失衡发生
- 复衡后子树的高度未必复原，更高的祖先可能随之失衡；
- 失衡会沿着祖先向上传播，因此最多作 O (logn)次调整；
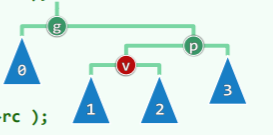
双旋：导致失衡（黄色方块）的局部在中间
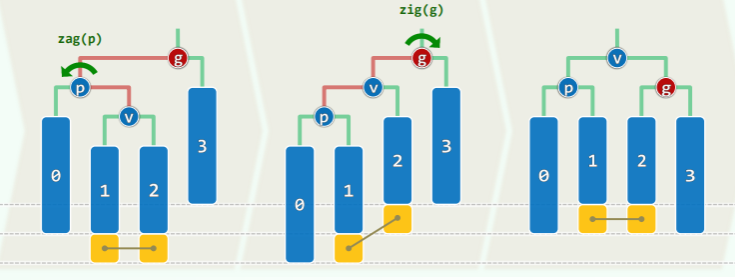
- 哪里出现失衡，就对其失衡的子树进行旋转，在对自身旋转。
- 同样失衡会继续向上传播，最多要作 O (logn)次调整。
- 经 Knuth 测试、统计指出，平均而言仅需 0.21 次旋转即可恢复平衡。

template <typename T>
bool AVL<T>::remove( const T & e ) {
	BinNodePosi<T> & x = search( e );
	if ( !x ) return false; //若目标的确存在

	removeAt( x, _hot ); _size--; //则在按BST规则删除之后，_hot及祖先均有可能失衡
	// 以下，从_hot出发逐层向上，依次检查各代祖先g
	for ( BinNodePosi<T> g = _hot; g; g = g->parent ) {
		if ( ! AvlBalanced( *g ) ) //一旦发现g失衡，则通过调整恢复平衡
			g = FromParentTo( *g ) = rotateAt( tallerChild( tallerChild( g ) ) );
		updateHeight( g ); //更新高度（注意：即便g未曾失衡或已恢复平衡，高度均可能降低）
	} //可能需做过Ω(logn)次调整；无论是否做过调整，全树高度均可能下降
	return true; //删除成功
}

即便删除未导致失衡，AVL 树的高度也可能降低；

3+4 重构

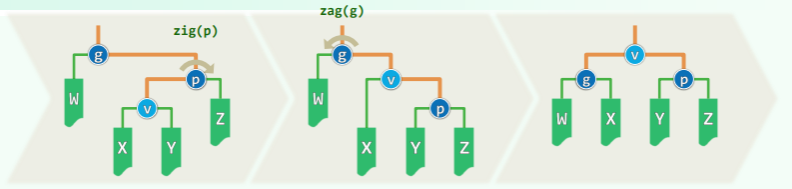
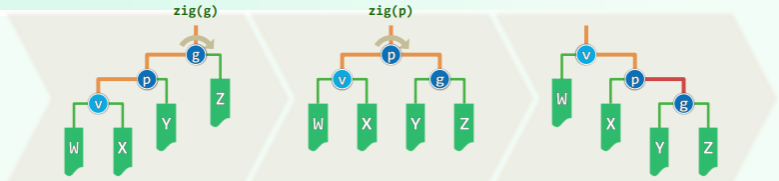
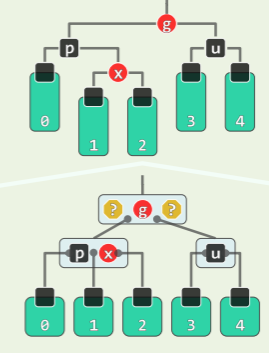
旋转所涉及的局部操作可以通过替换失衡节点的子树来完成，称为 3+4 重构（3 个节点，4 个子树）：

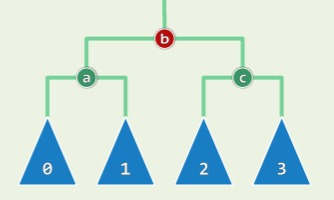
设 g 为最低失衡节点，考查其祖孙三代：gpv，按中序遍历次序分别命名 g 及其左右孩子为 b、a、c；
对 g 的孙节点及子树（无论是否为空），重命名为 T0 < T1 < T2 < T3；
旋转的本质就是在这个局部进行等价变换，并且要求保证中序遍历的次序不变：T0 < a < T1 < b < T2 < c < T3

/**
 * 按照“3 + 4”结构联接3个节点及其四棵子树，返回重组之后的局部子树根节点位置（即b）
 * 子树根节点与上层节点之间的双向联接，均须由上层调用者完成
 * 可用于AVL和RedBlack的局部平衡调整
 **/
template <typename T> BinNodePosi<T> BST<T>::connect34 (
   BinNodePosi<T> a, BinNodePosi<T> b, BinNodePosi<T> c,
   BinNodePosi<T> T0, BinNodePosi<T> T1, BinNodePosi<T> T2, BinNodePosi<T> T3
) {
   /*DSA*///print(a); print(b); print(c); printf("\n");
   a->lc = T0; if ( T0 ) T0->parent = a;
   a->rc = T1; if ( T1 ) T1->parent = a; updateHeight ( a );
   c->lc = T2; if ( T2 ) T2->parent = c;
   c->rc = T3; if ( T3 ) T3->parent = c; updateHeight ( c );
   b->lc = a; a->parent = b;
   b->rc = c; c->parent = b; updateHeight ( b );
   return b; //该子树新的根节点
}

之后来实现旋转操作：

/**
 * BST节点旋转变换统一算法（3节点 + 4子树），返回调整之后局部子树根节点的位置
 * 注意：尽管子树根会正确指向上层节点（如果存在），但反向的联接须由上层函数完成
 **/
template <typename T> BinNodePosi<T> BST<T>::rotateAt( BinNodePosi<T> v ) { //v为非空孙辈节点
   
   BinNodePosi<T> p = v->parent; 
   BinNodePosi<T> g = p->parent;
	
   //视v、p和g相对位置分四种情况
   if ( IsLChild( *p ) ) // zig
      if ( IsLChild( *v ) ) { /* zig-zig */
         p->parent = g->parent; //向上联接
         return connect34( v, p, g, v->lc, v->rc, p->rc, g->rc );
      } else { /* zig-zag */ 
         v->parent = g->parent; //向上联接
         return connect34( p, v, g, p->lc, v->lc, v->rc, g->rc );
      }
   else // zag
      if ( IsRChild( *v ) ) { /* zag-zag */ 
         p->parent = g->parent; //向上联接
         return connect34( g, p, v, g->lc, p->lc, v->lc, v->rc );
      } else { /* zag-zig */ 
         v->parent = g->parent; //向上联接
         return connect34( g, v, p, g->lc, v->lc, v->rc, p->rc );
      }
}

zig-zig:
zig-zag:
zag-zag:
zag-zig:

性能分析

优点：无论查找、插入、删除，最坏情况的时间复杂度均为 O(logn)，空间复杂度 O(n)
缺点：
- 平衡因子需要改造元素的数据域，或者额外封装；
- 插入、删除的旋转消耗的时间成本还是很高，并且删除操作最多作 Ω(logn) 次
- 对频繁的插入、删除操作支持不好；
- 单次调整可能导致全树拓扑变化量为 Ω(logn) —— 不利于版本管理（红黑树的优势）；

Splay Tree

局部性

计算机基础理论之一——局部性原理：在 BST 中刚被访问过的节点，极有可能再次被访问，并且可能下一个访问的节点就在刚访问过的节点的附近。

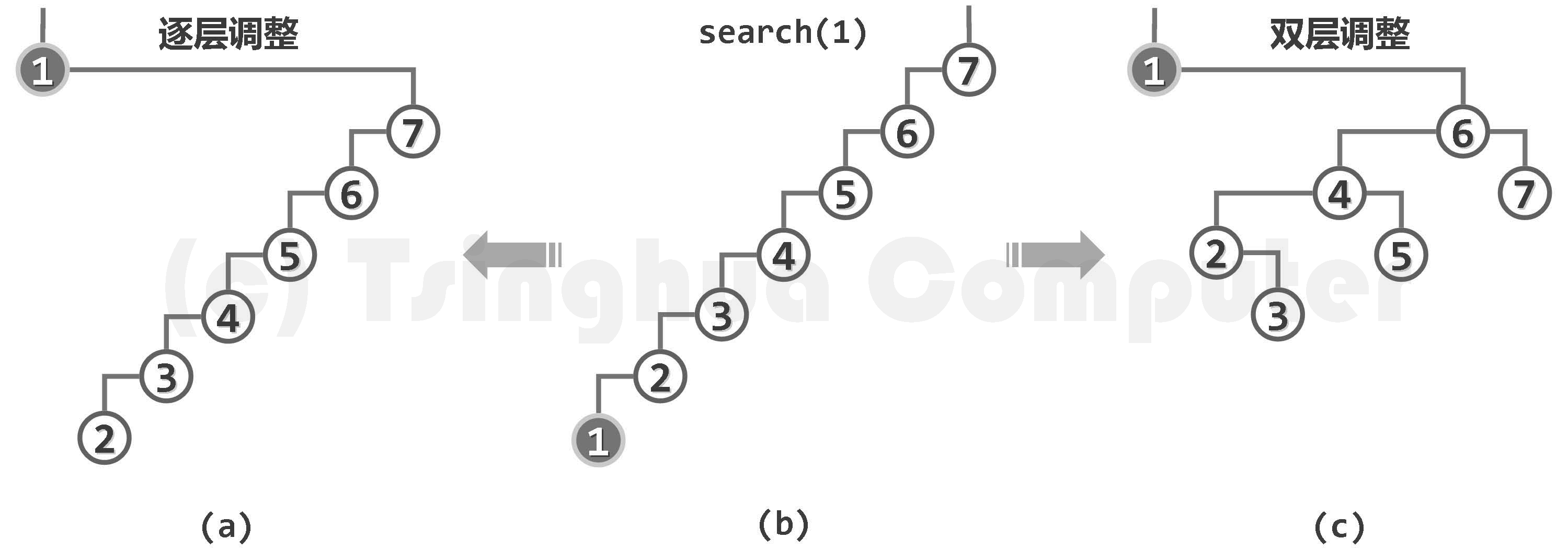
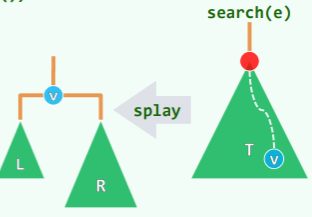
对 AVL 树的连续 m 次查找，共需 O (mlogn)时间，当 m 接近于 n 或超越 n 的数量级时，显然非常低效。思考自调整链表的思路——节点一旦被访问，随即移动到最前端。

将这个思路应用到 BST——节点一旦被访问，调整至树根。那么如何进行调整呢？最直接地，逐层旋转调整，一步步爬升至根：

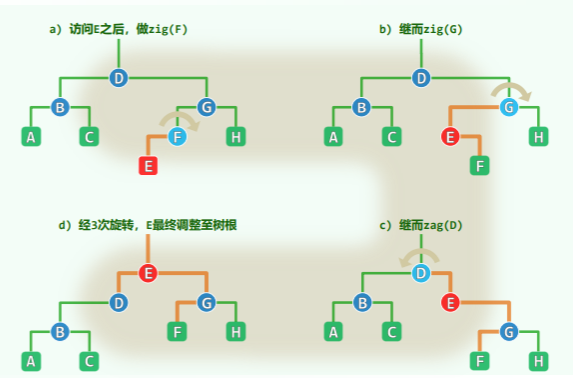
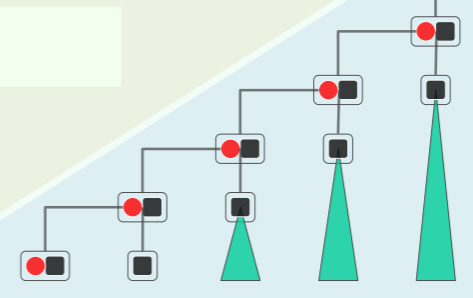
显然伸展（旋转、攀爬）的效率取决于树的初始形态和查找节点的访问次序，考虑最坏情况——单侧链的 BST，旋转次数是周期性的算术级数，每一周期为 Ω(n^2)，分摊为 Ω(n)：

双层伸展

核心操作：反复考查祖孙三代 gpv，根据相对位置经过两次旋转，使得 v 上升两层成为子树的根。

zig-zag/zag-zig

此时 v 按中序遍历次序为居中，若要成为根，则需进行两次方向不同的旋转：

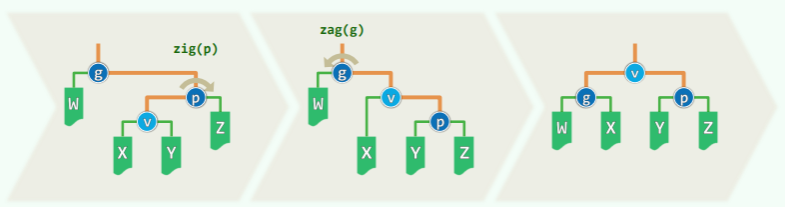
看起来与逐层调整没什么区别…
但其实精髓不在这里，因为这种情况里 v 想要上升为根，必须如此旋转。

zig-zig/zag-zag

此时 v 在中序遍历居左或居右的位置，若要成为根，则需进行两次方向相同的旋转，但是问题在于从 v 旋转还是从 g 旋转：

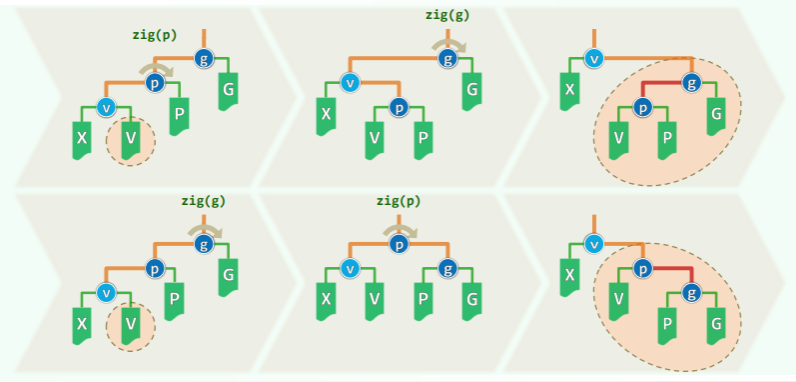
从 v 开始一层层向上旋转，如图第一行（逐层伸展）；
从 g 开始一层层向下旋转，如图第二行（双层伸展）；

在这个局部很难看出差异，但局部的细微差异导致全局的不同——tarjan 双层伸展：

可以看到，节点访问之后，对应路径的长度随即折半，使得最坏情况不致于持续发生。伸展操作的分摊时间仅需 O (logn)时间！

在习题集 8-2 Splay Tree的各操作分摊时间复杂度为O(logn) 中有详细证明。

zig/zag

最后不要忘记，v 只有父亲没有祖父的情况：v 在操作的最后，仅次于根节点处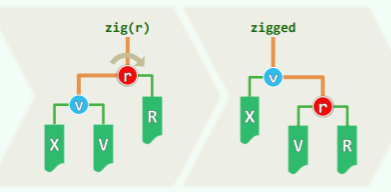：此时必有 v.parent () == T.root ()，只需要单次旋转即可，并且每轮伸展最多发生一次。

伸展实现

// 伸展树的接口
template <typename T> 
class Splay : public BST<T> { //由BST派生
protected:
	BinNodePosi<T> splay( BinNodePosi<T> v ); //将v伸展至根
public: //伸展树的查找也会引起整树的结构调整，故search()也需重写
	BinNodePosi<T> & search( const T & e ); //查找（重写）
	BinNodePosi<T> insert( const T & e ); //插入（重写）
	bool remove( const T & e ); //删除（重写）
};

// 伸展算法
template <typename NodePosi> inline 
//在节点*p与*lc（可能为空）之间建立父（左）子关系
void attachAsLC( NodePosi lc, NodePosi p ) { 
	p->lc = lc; 
	if ( lc ) lc->parent = p; 
}

template <typename NodePosi> inline 
//在节点*p与*rc（可能为空）之间建立父（右）子关系
void attachAsRC( NodePosi p, NodePosi rc ) { 
	p->rc = rc; 
	if ( rc ) rc->parent = p; 
}

template <typename T> 
//Splay树伸展算法：从节点v出发逐层伸展
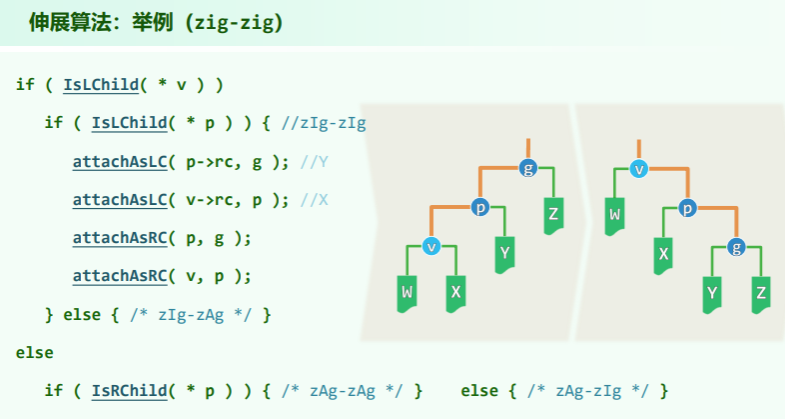
BinNodePosi<T> Splay<T>::splay( BinNodePosi<T> v ) { 
	// v为因最近访问而需伸展的节点位置
    if ( !v ) return NULL; 
    BinNodePosi<T> p; BinNodePosi<T> g; //*v的父亲与祖父
    while ( ( p = v->parent ) && ( g = p->parent ) ) { 
		//自下而上，反复对*v做双层伸展
	    BinNodePosi<T> gg = g->parent; //每轮之后*v都以原曾祖父（great-grand parent）为父
	    if ( IsLChild( *v ) )
		    if ( IsLChild( *p ) ) { // zig-zig
	            attachAsLC( p->rc, g ); 
	            attachAsLC( v->rc, p );
	            attachAsRC( p, g ); 
	            attachAsRC( v, p );
        } else { //zig-zag
            attachAsLC( v->rc, p ); 
            attachAsRC( g, v->lc );
            attachAsLC( g, v ); 
            attachAsRC( v, p );
        }
	    else
	        if ( IsRChild ( *p ) ) { //zag-zag
	            attachAsRC( g, p->lc ); 
	            attachAsRC( p, v->lc );
	            attachAsLC( g, p ); 
	            attachAsLC( p, v );
         } else { //zag-zig
	            attachAsRC( p, v->lc ); 
	            attachAsLC( v->rc, g );
	            attachAsRC( v, g ); 
	            attachAsLC( p, v );
         }
	    if ( !gg ) v->parent = NULL; //若*v原先的曾祖父*gg不存在，则*v现在应为树根
	    else //否则，*gg此后应该以*v作为左或右孩子
         ( g == gg->lc ) ? attachAsLC( v, gg ) : attachAsRC( gg, v );
		updateHeight( g ); 
		updateHeight( p ); 
		updateHeight( v );
    } //双层伸展结束时，必有g == NULL，但p可能非空
	
	if ( p = v->parent ) { 
	//若p果真非空，则额外再做一次单旋
		if ( IsLChild( *v ) ) { 
			attachAsLC( v->rc, p ); 
			attachAsRC( v, p ); 
		} else { 
			attachAsRC ( p, v->lc ); 
			attachAsLC ( p, v ); 
		}
	    updateHeight( p ); 
	    updateHeight( v );
    }
    v->parent = NULL; 
    return v;
} //调整之后新树根应为被伸展的节点，故返回该节点的位置以便上层函数更新树根

查找

template <typename T> 
BinNodePosi<T> & Splay<T>::search( const T & e ) {
	// 调用标准BST的内部接口定位目标节点
	BinNodePosi<T> p = BST<T>::search( e );
	// 无论成功与否，最后被访问的节点都将伸展至根
	_root = splay( p ? p : _hot ); //成功、失败
	// 总是返回根节点
	return _root;
}

伸展树的查找，与常规 BST::search()不同：很可能会改变树的拓扑结构，不再属于静态操作。

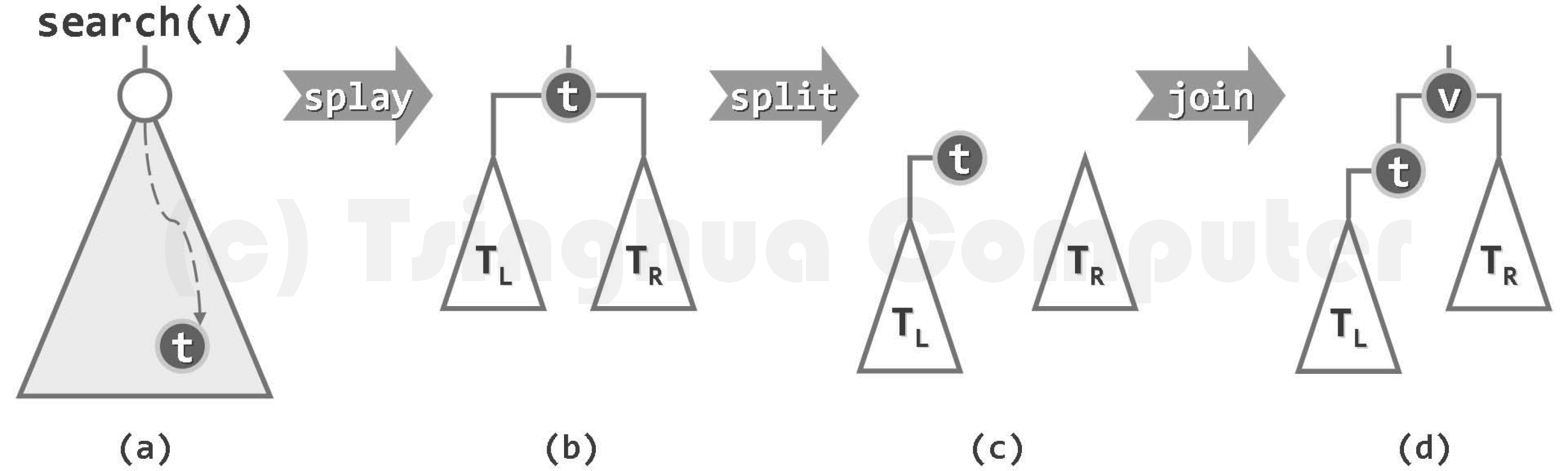
插入

除了直观地先查找、再插入、最后伸展至树根，我们可以直接在查找失败时直接在树根附近插入新节点：

template <typename T> 
BinNodePosi<T> Splay<T>::insert( const T & e ) {
	if ( !_root ) { 
		_size = 1; 
		return _root = new BinNode<T>( e ); 
	} //原树为空
	
	BinNodePosi<T> t = search( e ); 
	if ( e == t->data ) return t; //t若存在，伸展至根
	if ( t->data < e ) { 
		//在右侧嫁接（rc或为空，lc == t必非空）
		t->parent = _root = new BinNode<T>( e, NULL, t, t->rc ); //lc==t必非空
		if ( t->rc ) { //rc或为空
			t->rc->parent = _root; 
			t->rc = NULL; 
		}
	} else { 
	//e < t->data，在左侧嫁接（lc或为空，rc == t必非空）
		t->parent = _root = new BinNode<T>( e, NULL, t->lc, t );
		if ( t->lc ) { 
			t->lc->parent = _root; 
			t->lc = NULL; 
		}
	}
	
	_size++; 
	updateHeightAbove( t ); 
	return _root; //更新规模及t与_root的高度，插入成功
} //无论如何，返回时总有_root->data == e

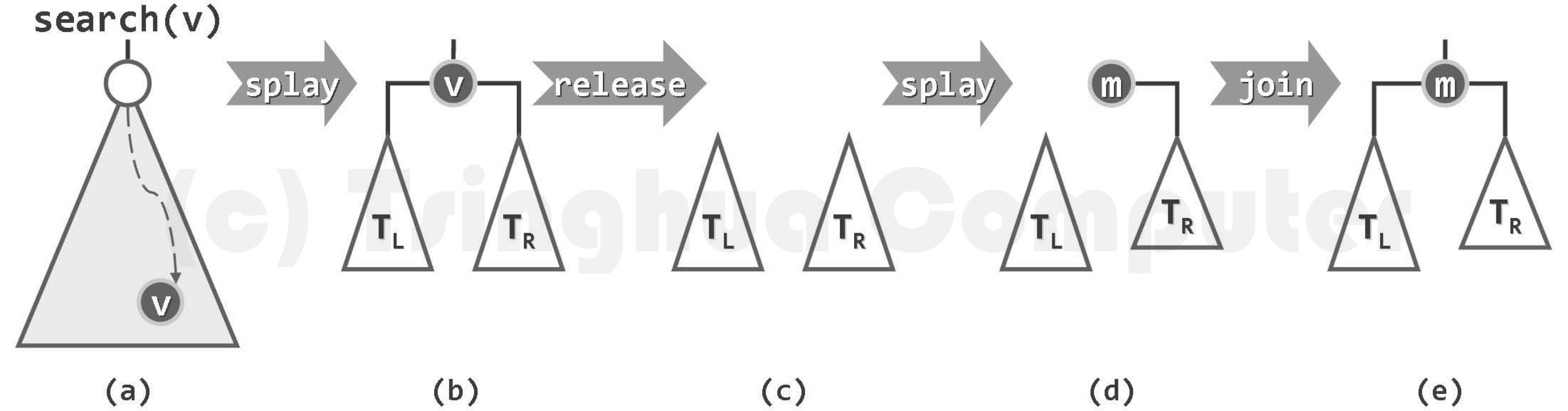
删除

直观地，查找到对应节点后删除之，再将_hot 伸展至根。可以考虑先伸展至树根，再于树根附近直接摘除目标节点：

template <typename T> 
bool Splay<T>::remove( const T & e ) {
	if ( !_root || ( e != search( e )->data ) ) 
		return false; 
		
	//若目标存在，则伸展至根
	BinNodePosi<T> L = _root->lc, R = _root->rc; release(_root); //记下子树后，释放之
	if ( !R ) { //若R空
		if ( L ) L->parent = NULL; _root = L; //则L即是余树
	} else { //否则
		_root = R; R->parent = NULL; search( e ); //在R中再找e：注定失败，但最小节点必
		if (L) L->parent = _root; _root->lc = L; //伸展至根，故可令其以L作为左子树
	}
	_size--; if ( _root ) updateHeight( _root ); //更新记录
	return true; //删除成功
}

性能分析

Splay Tree 的优点：

无需记录高度或平衡因子；
编程实现简单——优于 AVL 树；
分摊复杂度 O (logn) ——与 AVL 树相当 (不考虑局部性时才会降低至此，因此在多次、具有局部性的查找中效率突破了 O (logn) )
局部性强、缓存命中率极高时（即下图中 k << n << m 时，m 是查找次数）
- 效率甚至可以更高——自适应的 O (logk)
- 任何连续的 m 次查找，仅需 O (mlogk+nlogn) 时间
- 若反复地顺序访问任一子集，分摊成本仅为常数；

Splay Tree 的缺点：

不能杜绝单次最坏情况，不适用于对效率敏感的场合
复杂度的分析稍显复杂——好在有初等的证明：势能分析

势能分摊分析

Splay Tree 操作的复杂度的势能分析

势能定义

任何时刻的任何一棵伸展树 S，都可以假想地认为具有势能：

Φ (S) = lo g (v \in S \prod s i ze (v)) = v \in S \sum lo g (s i ze (v)) = v \in S \sum r ank (v) = v \in S \sum lo g V

符合直觉的：越平衡的树，势能越小（树高越低）；越倾侧的树，势能越大（树高越高）

单链的势能： $Φ (S) = lo g n! = O (n lo g n)$
满树的势能：

Φ (S) = lo g d = 0 \prod h (2^{h - d + 1} - 1)^{2^{d}} \leq lo g d = 0 \prod h (2^{h - d + 1})^{2^{d}} = lo g d = 0 \prod h 2^{(h - d + 1) \cdot 2^{d}} = d = 0 \sum h (h - d + 1) \cdot 2^{d} = (h + 1) d = 0 \sum h 2^{d} - d = 0 \sum h d \cdot 2^{d} = (h + 1) \cdot (2^{h + 1} - 1) - [(h - 1) \cdot 2^{h + 1} + 2] = 2^{h + 2} - h - 3 = O (n)

调整时间的上界

考查对伸展树 S 的 m 次连续访问 (m >> n，不妨仅考查 search() )

记第 k 次操作的分摊复杂度取作实际复杂度与势能变化量之和： $A^{(k)} = T^{(k)} + Δ Φ^{(k)}, k = 0, 1, 2, ..., m$ ，则有： $A - O (n lo g n) \leq T = A - ΔΦ \leq A + O (n lo g n)$

只要能够确定 A=O (mlogn)，则必有 T=O (mlogn)。

实际上， $A^{(k)}$ 永远不致超过节点 v 的势能变化量： $O (r an k^{(k)} (v) - r an k^{(k - 1)} (v)) = O (lo g n)$ 。 $A^{(k)}$ 的本质是对 v 作若干次连续伸展操作的时间成本之累积，这些操作无非三种情况：

zig/zag

A^{(k)} = T^{(k)} + ΔΦ (S_{i}^{(k)}) = 1 + Δ r an k_{i} (v) + Δ r an k_{i} (r) = 1 + [r an k_{i} (v) - r an k_{i - 1} (v)] + [r an k_{i} (r) - r an k_{i - 1} (r)] < 1 + [r an k_{i} (v) - r an k_{i - 1} (v)]

zig-zag/zag-zig

A^{(k)} = T^{(k)} + ΔΦ (S_{i}^{(k)}) = 2 + Δ r an k_{i} (g) + Δ r an k_{i} (p) + Δ r an k_{i} (v) = 2 + [r an k_{i} (g) - r an k_{i - 1} (g)] + [r an k_{i} (p) - r an k_{i - 1} (p)] + [r an k_{i} (v) - r an k_{i - 1} (v]) < 2 + r an k_{i} (g) + r an k_{i} (p) - 2 \cdot r an k_{i - 1} (v) (1) < 2 + 2 \cdot r an k_{i} (v) - 2 - 2 \cdot r an k_{i - 1} (v) (2) = 2 \cdot (r an k_{i} (v) - r an k_{i - 1} (v))

放缩的原理是： $r an k_{i - 1} (p) > r an k_{i - 1} (v)$
放缩的原理是： $\frac{l o g G _{i} + l o g P _{i}}{2} \leq lo g \frac{G _{i} + P _{i}}{2} < lo g \frac{V _{i}}{2}$

zig-zig/zag-zag

A^{(k)} = T^{(k)} + ΔΦ (S_{i}^{(k)}) = 2 + Δ r an k_{i} (g) + Δ r an k_{i} (p) + Δ r an k_{i} (v) = 2 + [r an k_{i} (g) - r an k_{i - 1} (g)] + [r an k_{i} (p) - r an k_{i - 1} (p)] + [r an k_{i} (v) - r an k_{i - 1} (v]) < 2 + r an k_{i} (g) + r an k_{i} (p) - 2 \cdot r an k_{i - 1} (v) (1) < 2 + r an k_{i} (g) + r an k_{i} (v) - 2 \cdot r an k_{i - 1} (v) (2) < 3 \cdot (r an k_{i} (v) - r an k_{i - 1} (v)) (3)

放缩的原理是： $r an k_{i - 1} (p) > r an k_{i - 1} (v)$
放缩的原理是： $r an k_{i} (p) < r an k_{i} (v)$
放缩的原理是： $\frac{l o g G _{i} + l o g V _{i - 1}}{2} \leq lo g \frac{G _{i} + V _{i - 1}}{2} < lo g \frac{V _{i}}{2}$

B-Tree

背景

存储器容量的增长速度 << 应用问题规模的增长速度
因此相对而言，存储器的容量甚至在不断减小
- 典型数据库规模/内存容量：
- 1990： 10MB / 2MB = 5
- 2020: 10TB / 10GB = 1000
在特定工艺及成本下，存储器都是容量与速度折中的产物
实用的存储系统，由不同类型的存储器级联得到，而内存的访问速度与外存的访问速度的数量级差距之大，可达 10000 倍甚至更多。因此最大限度地利用数据访问的局部性，多多地访问内存。
策略：常用的数据，复制到更高层、更小的存储器中，找不到，才向更低层、更大的存储器索取；
此时算法的实际运行时间，将取决于相邻存储级别之间数据 I/O 的速度与次数；
并且外存是块设备，以页、段为块单位进行传送，读 1B 和读 1 块的用时基本相同，借助缓冲区，可以大大缩短单位字节的平均访问时间。
因此算法的主要优化目标是，如何提高缓冲策略的命中率。

特点

每 d 代合并为超级节点，则除根节点外每个节点分 m=2^d 路，每个节点最多 m-1 个关键码；
思考在访问外存期间 BTree 的优势：
- 若 n=1G 个记录，对 AVL 树而言查找需要 $lo g_{2} 1 0^{9}$ 次 I/O，每次只读单个关键码，代价太大；
- 对 B-Tree，充分利用外存的批量访问，每下降一层，都以超级节点为单位读入一组关键码；
- 具体多大视数据块的大小确定，m=keys_num / page，通常 m=200~300；
- 以 m=256 为例，每次查找只需 $lo g_{256} 1 0^{9} < 4$ 次 I/O

准确定义

终于，对 BTree 作一个准确定义：

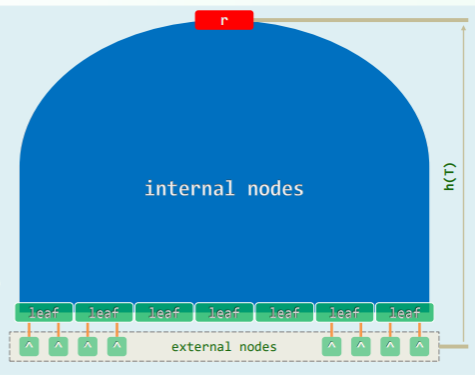
m 阶 BTree，即 m 路完全平衡搜索树，外部节点的深度统一相等，以该深度作 BTree 的树高h
注意以此定义，根节点深度为 0，外部节点的高度为 0，叶节点高度为 1；
叶节点的深度统一为 h-1，也相等；
内部节点
- 最多含 m-1 个关键码，每个关键码以升序排列（有序就行），
- 每个关键码对应小于自身一个左分支，最后一个关键码右侧有一个大于自身的右分支，即分支数最多 m 个
- 树根的分支不能小于 2（即 1 个关键码），其它内部节点的分支不能小于 $⌈ \frac{m}{2} ⌉$ ，（即关键码不小于 $⌈ \frac{m}{2} ⌉ - 1$ ）
故 BTree 的准确名称为： $(⌈ \frac{m}{2} ⌉, m)$ - B 树

举例

m = 3：2-3-树，(2,3)-树
- 最简单的 B-树 //J. Hopcroft, 1970
- 各（内部）节点的分支数，可能是 2 或 3
- 各节点所含 key 的数目，可能是 1 或 2
m = 4：2-4-树，(2,4)-树
- 各节点的分支数，可能是 2、3 或 4
- 各节点所含 key 的数目，可能是 1、2 或 3
- 红黑树就是一种 (2,4)-树。

ADT

// BTNode
template <typename T> 
struct BTNode { //B-树节点
	BTNodePosi<T> parent; //父
	Vector<T> key; //关键码
	Vector< BTNodePosi<T> > child; //孩子
	BTNode() { parent = NULL; child.insert( NULL ); }
	BTNode( T e, BTNodePosi<T> lc = NULL, BTNodePosi<T> rc = NULL ) {
		parent = NULL; //作为根节点
		key.insert( e ); //仅一个关键码，以及
		child.insert( lc ); 
		if ( lc ) lc->parent = this; //左孩子
		child.insert( rc ); 
		if ( rc ) rc->parent = this; //右孩子
	}
};

// BTree
template <typename T> using BTNodePosi = BTNode<T>*; //B-树节点位置
template <typename T> 
class BTree { //B-树
protected:
	Rank _size, _m; //关键码总数、阶次
	BTNodePosi<T> _root, _hot; //根、search()最后访问的非空节点
	void solveOverflow( BTNodePosi<T> ); //因插入而上溢后的分裂处理
	void solveUnderflow( BTNodePosi<T> ); //因删除而下溢后的合并处理

public:
	BTree( int m = 3 ) : _m( m ), _size( 0 ) {
		//构造函数：默认为最低的3阶
		_root = new BTNode<T>(); 
	}
	~BTree() { 
		//析构函数：释放所有节点
		if ( _root ) release( _root ); 
	} 
   int const order() { return _m; } //阶次
   int const size() { return _size; } //规模
   BTNodePosi<T> & root() { return _root; } //树根
   bool empty() const { return !_root; } //判空
   BTNodePosi<T> search ( const T& e ); //查找
   bool insert ( const T& e ); //插入
   bool remove ( const T& e ); //删除
};

查找

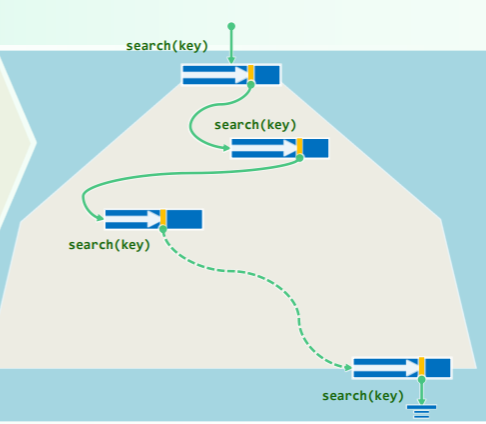
BTree 的根节点常驻 RAM 中，查找步骤如下：

只要当前节点不是外部节点
- 在当前节点中顺序查找（二分亦可，但效率提升并不明显）
- 若找到目标关键码，则
  - 返回查找成功
- 否则
  - 沿引用向下搜索，在孩子节点中查找（I/O 耗时）
  - 若找到，则读入内存中
返回查找失败

template <typename T> 
BTNodePosi<T> BTree<T>::search( const T & e ) {
	BTNodePosi<T> v = _root;
	_hot = NULL; //从根节点出发
	while ( v ) { //逐层深入地
		Rank r = v->key.search( e ); //在当前节点对应的向量中顺序查找
		if ( 0 <= r && e == v->key[r] ) return v; //若成功，则返回；否则...
		_hot = v; v = v->child[ r + 1 ]; //沿引用转至对应的下层子树，并载入其根（I/O）
	} //若因!v而退出，则意味着抵达外部节点
	return NULL; //失败
}

性能

约定：

根节点常驻 RAM,
内存中查找耗时忽略，（相比于 I/O 的耗时实在是微乎其微，相差 10^4 倍以上）
运行时间主要取决于 I/O 次数，
每个深度最多进行一次 I/O

故，

search 需要的运行时间= $O (lo g_{m} n)$

树高

树高 h： $lo g_{m} (N + 1) \leq h \leq 1 + ⌊ lo g_{⌈ \frac{m}{2} ⌉} \frac{N + 1}{2} ⌋$
- 左边对应树高最低情况，即每个节点都有 m 路分支
- 右边对应树高最高情况，即每个节点都有 $⌈ \frac{m}{2} ⌉$ 路分支

插入

template <typename T> 
bool BTree<T>::insert( const T & e ) {
	BTNodePosi<T> v = search( e );
	if ( v ) return false; //确认e不存在
	Rank r = _hot->key.search( e ); //在节点_hot中确定插入位置
	_hot->key.insert( r+1, e ); //将新关键码插至对应的位置
	_hot->child.insert( r+2, NULL ); _size++; //创建一个空子树指针
	solveOverflow( _hot ); //若上溢，则分裂
	return true; //插入成功
}

分裂

若上溢节点中关键码为 ${k_{0}, k_{1}, ..., k_{m - 1}}$ ，取中位数 $s = ⌊ \frac{m}{2} ⌋$ ，则以关键码 $k_{s}$ 划分为： ${k_{0}, k_{1}, ..., k_{s - 1}}$ ${k_{s}}$ ${k_{s + 1}, ..., k_{m - 1}}$
关键码 $k_{s}$ 上升一层，分裂所得到的两个（超级）节点作左右孩子
若上溢的节点导致父节点溢出，则继续会发生上溢分裂
上溢传播最坏情况不过也就是到根，若在根节点也导致上溢分裂，则树高增加 1；
总体执行时间正比于分裂次数 O (h)

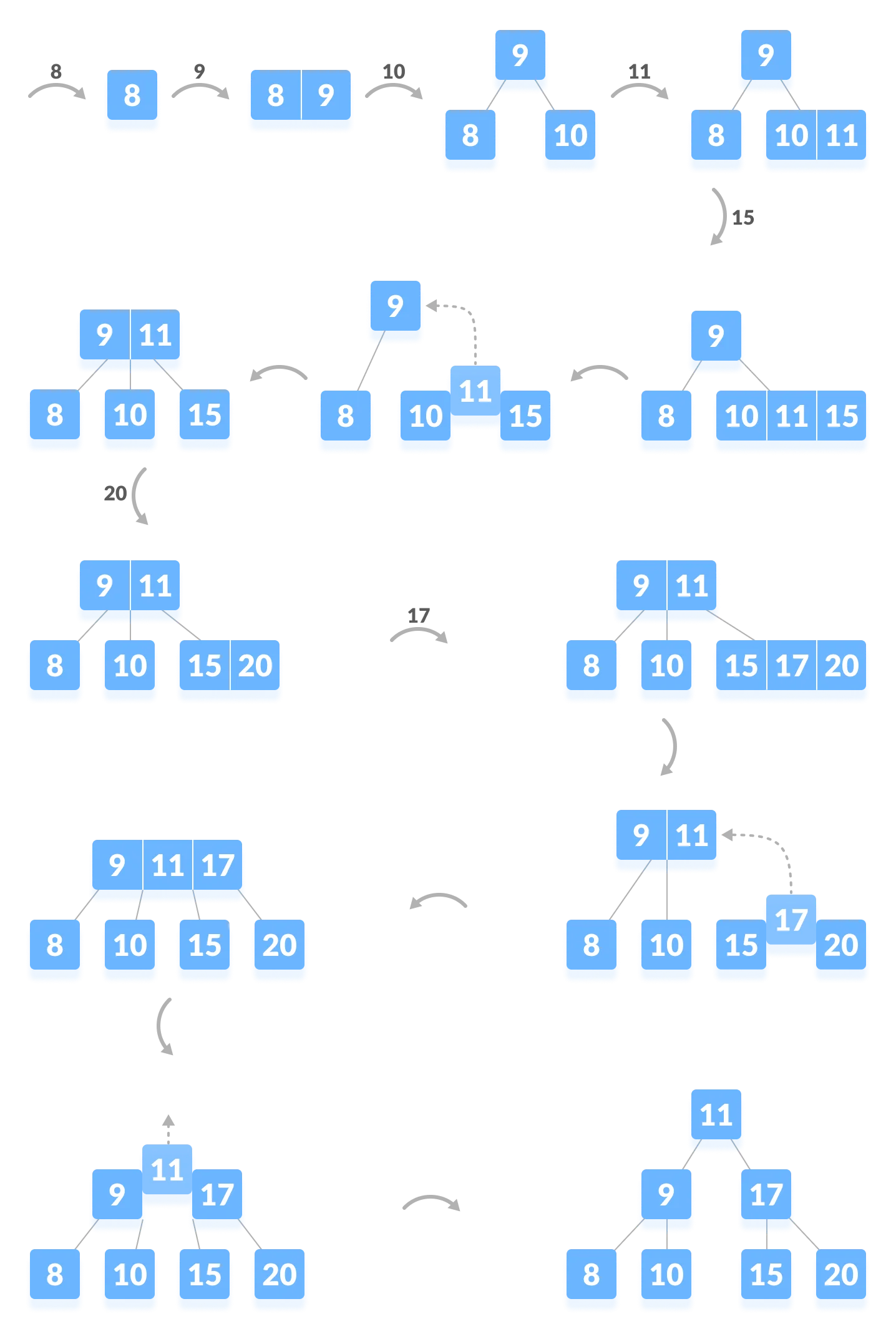
Insert-Example

指向原始笔记的链接

上溢修复

template <typename T> //关键码插入后若节点上溢，则做节点分裂处理
void BTree<T>::solveOverflow( BTNodePosi<T> v ) {
	while ( _m <= v->key.size() ) {//除非当前节点并未上溢
		//划分轴点
		//此时应有_m = key.size() = child.size() - 1
	    Rank s = _m / 2; 
	    BTNodePosi<T> u = new BTNode<T>(); //注意：新节点已有一个空孩子
	    for ( Rank j = 0; j < _m - s - 1; j++ ) { 
		    // v右侧_m-s-1个孩子及关键码分裂为右侧节点u
	        u->child.insert( j, v->child.remove( s + 1 ) ); //逐个移动效率低
	        u->key.insert( j, v->key.remove( s + 1 ) ); //此策略可改进
		}
		u->child[_m - s - 1] = v->child.remove( s + 1 ); //移动v最靠右的孩子
	    if ( u->child[0] ) //若u的孩子们非空，则
	        for ( Rank j = 0; j < _m - s; j++ ) //令它们的父节点统一
            u->child[j]->parent = u; //指向u
	    BTNodePosi<T> p = v->parent; // v当前的父节点p
	    if ( !p ) { 
		    _root = p = new BTNode<T>(); 
		    p->child[0] = v; 
		    v->parent = p; } //若p空则创建之
	    Rank r = 1 + p->key.search( v->key[0] ); // p中指向v的指针的秩
	    p->key.insert( r, v->key.remove( s ) ); //轴点关键码上升
	    p->child.insert( r + 1, u ); u->parent = p; //新节点u与父节点p互联
	    v = p; //上升一层，如有必要则继续分裂――至多O(logn)层
	} //while
}

删除

template <typename T> 
bool BTree<T>::remove( const T& e ) { 
	//从BTree树中删除关键码e
	BTNodePosi<T> v = search( e ); 
	if ( !v ) return false; //确认目标关键码存在
	Rank r = v->key.search( e ); //确定目标关键码在节点v中的秩（由上，肯定合法）
	if ( v->child[0] ) { //若v非叶子，则e的后继必属于某叶节点
	    BTNodePosi<T> u = v->child[r + 1]; //在右子树中一直向左，即可
	    while ( u->child[0] ) u = u->child[0]; //找出e的后继
	    v->key[r] = u->key[0]; v = u; r = 0; //并与之交换位置
	} //至此，v必然位于最底层，且其中第r个关键码就是待删除者
	v->key.remove( r ); 
	v->child.remove( r + 1 ); 
	_size--; //删除e，以及其下两个外部节点之一
	solveUnderflow( v ); //如有必要，需做旋转或合并
	return true;
}

非根节点 V 需要下溢时，恰有 $⌈ \frac{m}{2} ⌉ - 2$ 个关键码和 $⌈ \frac{m}{2} ⌉ - 1$ 个分支，视其兄弟 L 或 R 的规模，可分三种情况处理：

L 存在且至少包含 $⌈ \frac{m}{2} ⌉$ 个关键码
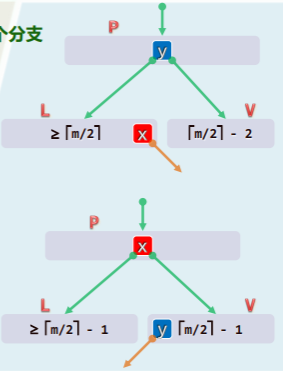
- 则将 P 中的分解关键码 y 移至 V 中作为最小关键码
- 将 L 中最大关键码 x 移至 P 中取代原关键码y
- 如此旋转后，局部乃至全树都重新满足 BTree 的条件
R 存在且至少包含 $⌈ \frac{m}{2} ⌉$ 个关键码
- 镜像地，旋转解决；
L 和 R 或不存在，或均不满足 $⌈ \frac{m}{2} ⌉$ 个关键码
- 即便如此，L 和 R 仍至少有一者恰含 $⌈ \frac{m}{2} ⌉ - 1$ 个关键码
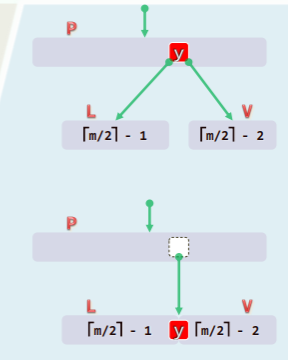
- 从 P 中抽出介于 L 和 V 之间的分解关键码 y，通过 y 将 L 和 V 合成一个节点，同时合并此前 y 的孩子引用；
- 若此处下溢得以修复，又可能导致 P 发生下溢，继而上升至根，但最多不过 O (h)层；

举例

Transclude of 71-BTree#case-i----delete-leaf

Transclude of 71-BTree#case-ii----delete-the-internals

注意看这里之所以发生下溢修复，是因为分支与关键码数不匹配，因此为之。

Case III - shrink height

In this case, the height of the tree shrinks. If the target key lies in an internal node, and the deletion of the key leads to a fewer number of keys in the node (i.e. less than the minimum required), then look for the inorder predecessor and the inorder successor. If both the children contain a minimum number of keys then, borrowing cannot take place. This leads to Case II (3) i.e. merging the children.

Again, look for the sibling to borrow a key. But, if the sibling also has only a minimum number of keys then, merge the node with the sibling along with the parent. Arrange the children accordingly (increasing order).

指向原始笔记的链接

下溢修复

template <typename T> //关键码删除后若节点下溢，则做节点旋转或合并处理
void BTree<T>::solveUnderflow( BTNodePosi<T> v ) {
	while ( ( _m + 1 ) / 2 > v->child.size() ) { //除非当前节点并未下溢
	    BTNodePosi<T> p = v->parent;
	    if ( !p ) { //已到根节点（两个孩子即可）
	        if ( !v->key.size() && v->child[0] ) {
	            //但倘若作为树根的v已不含关键码，却有（唯一的）非空孩子，则
	            _root = v->child[0]; 
	            _root->parent = NULL; //这个节点可被跳过
	            v->child[0] = NULL; 
	            release( v ); //并因不再有用而被销毁
	        } //整树高度降低一层
	        return;
	    }
	    Rank r = 0;
	    while ( p->child[r] != v ) r++;//确定v是p的第r个孩子――此时v可能不含关键码，故不能通过关键码查找
	    //另外，在实现了孩子指针的判等器之后，也可直接调用Vector::find()定位

		// 情况1：向左兄弟借关键码
	    if ( 0 < r ) { //若v不是p的第一个孩子，则
	        BTNodePosi<T> ls = p->child[r - 1]; //左兄弟必存在
	        if ( ( _m + 1 ) / 2 < ls->child.size() ) { //若该兄弟足够“胖”，则
	            v->key.insert( 0, p->key[r - 1] ); // p借出一个关键码给v（作为最小关键码）
	            p->key[r - 1] = ls->key.remove( ls->key.size() - 1 ); // ls的最大关键码转入p
	            v->child.insert( 0, ls->child.remove( ls->child.size() - 1 ) );
	            //同时ls的最右侧孩子过继给v
	            if ( v->child[0] ) v->child[0]->parent = v; //作为v的最左侧孩子
            return; //至此，通过右旋已完成当前层（以及所有层）的下溢处理
	        }
	    } //至此，左兄弟要么为空，要么太“瘦”

		// 情况2：向右兄弟借关键码
	    if ( p->child.size() - 1 > r ) { //若v不是p的最后一个孩子，则
	        BTNodePosi<T> rs = p->child[r + 1]; //右兄弟必存在
	        if ( ( _m + 1 ) / 2 < rs->child.size() ) { //若该兄弟足够“胖”，则
	            v->key.insert( v->key.size(),p->key[r] ); // p借出一个关键码给v（作为最大关键码）
	            p->key[r] = rs->key.remove( 0 ); // rs的最小关键码转入p
	            v->child.insert( v->child.size(), rs->child.remove( 0 ) );
	            //同时rs的最左侧孩子过继给v
	            if ( v->child[v->child.size() - 1] ) //作为v的最右侧孩子
		            v->child[v->child.size() - 1]->parent = v;
	            return; //至此，通过左旋已完成当前层（以及所有层）的下溢处理
	        }
	    } //至此，右兄弟要么为空，要么太“瘦”

		// 情况3：左、右兄弟要么为空（但不可能同时），要么都太“瘦”――合并
	    if ( 0 < r ) { //与左兄弟合并
	        BTNodePosi<T> ls = p->child[r - 1]; //左兄弟必存在
	        ls->key.insert( ls->key.size(), p->key.remove( r - 1 ) ); p->child.remove( r );
	        // p的第r - 1个关键码转入ls，v不再是p的第r个孩子
	        ls->child.insert( ls->child.size(), v->child.remove( 0 ) );
	        if ( ls->child[ls->child.size() - 1] ) // v的最左侧孩子过继给ls做最右侧孩子
		        ls->child[ls->child.size() - 1]->parent = ls;
	        while ( !v->key.empty() ) { // v剩余的关键码和孩子，依次转入ls
	            ls->key.insert( ls->key.size(), v->key.remove( 0 ) );
	            ls->child.insert( ls->child.size(), v->child.remove( 0 ) );
	            if ( ls->child[ls->child.size() - 1] ) 
		            ls->child[ls->child.size() - 1]->parent = ls;
		    }
	        release ( v ); //释放v
	    } else { //与右兄弟合并
	        BTNodePosi<T> rs = p->child[r + 1]; //右兄弟必存在
	        rs->key.insert( 0, p->key.remove( r ) ); p->child.remove( r );
	        // p的第r个关键码转入rs，v不再是p的第r个孩子
	        rs->child.insert( 0, v->child.remove( v->child.size() - 1 ) );
	        if ( rs->child[0] ) rs->child[0]->parent = rs; // v的最右侧孩子过继给rs做最左侧孩子
	        while ( !v->key.empty() ) { // v剩余的关键码和孩子，依次转入rs
	            rs->key.insert( 0, v->key.remove( v->key.size() - 1 ) );
	            rs->child.insert( 0, v->child.remove( v->child.size() - 1 ) );
	            if ( rs->child[0] ) rs->child[0]->parent = rs;
	        }
		    release( v ); //释放v
	    }
	    v = p; //上升一层，如有必要则继续旋转或合并――至多O(logn)层
	} //while
}

Red-black Tree

动机

并发性

BST 的访问需要稳定的结构——修改导致的结构变化，需要加锁，此时禁止其它进程访问该 BST，直到完成结构变化后解锁。（这一周期决定了访问 BST 的延迟）

Splay Tree 的结构变化剧烈——最差可达 O (n)
AVL Tree：remove 时为 O (logn)，insert 可以保证 O (1)
Red-black Tree：无论 insert 或 remove，都可以保证 O (1)
- Linux进程的CFS调度策略

持久性

若要实现 BST 对历史版本的访问，BF 方法是对每个版本独立保存、各版本自成一个搜索结构：

单次操作 O (logh+logn)，累计 O (n x h)的时间和空间。（此处 h 指 history 的数量）

若要实现复杂度控制在 O (n+hlogn)以内，则要利用相邻版本之间的相关性（历史版本在时间上连续，自然结构上有前后的相关性）：

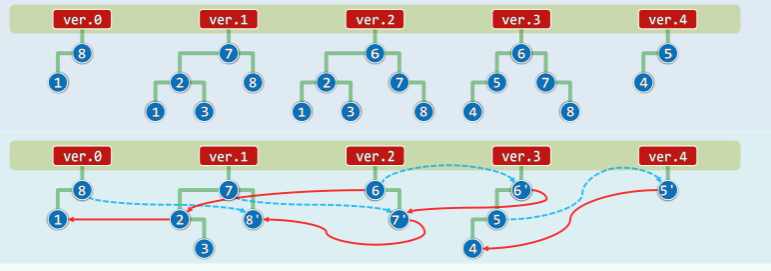
如此，就树形结构的拓扑而言，相邻版本之间的结构差异不超过 O (1)

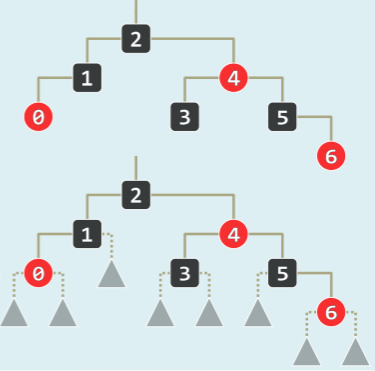
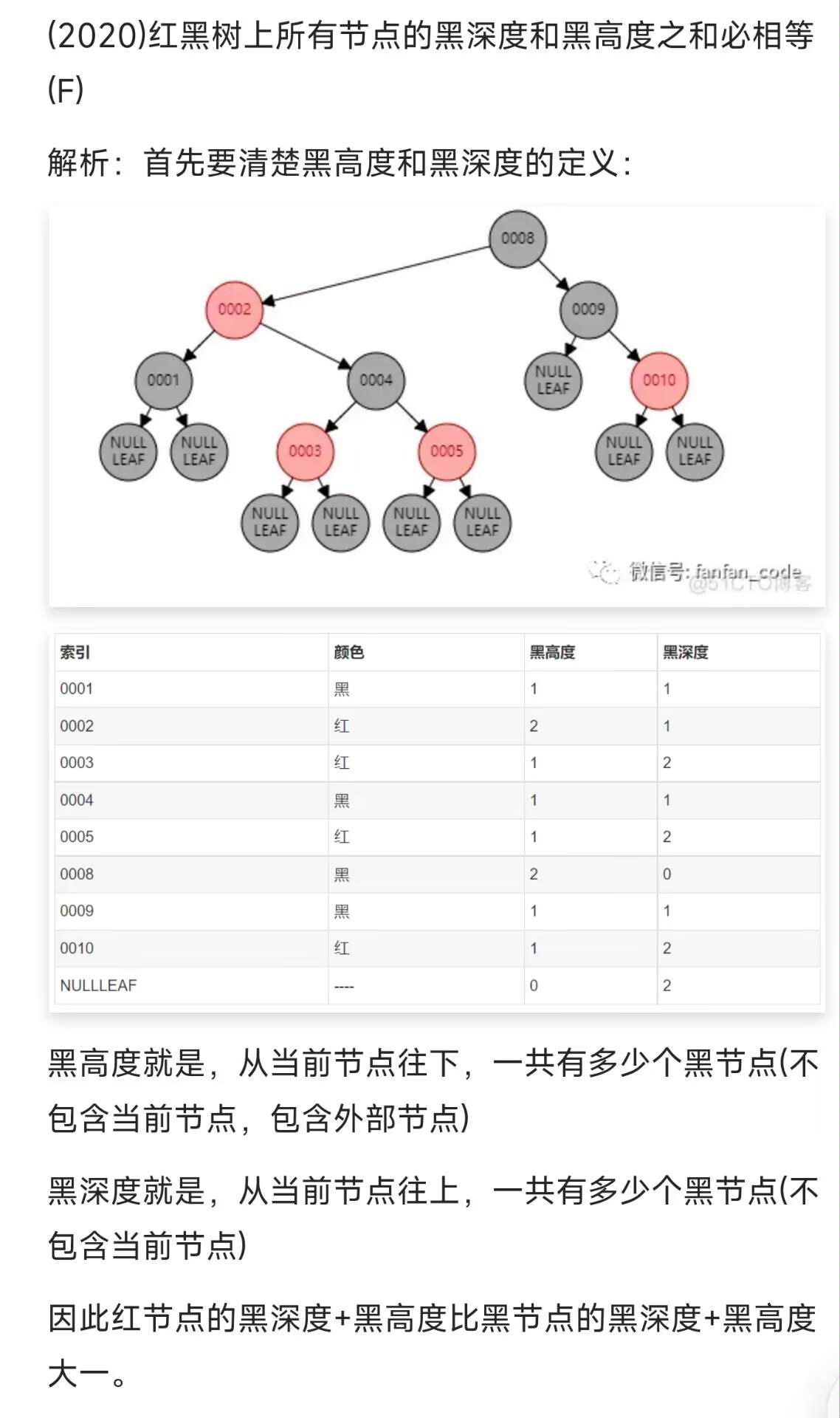
红黑树的规则

由红黑两类节点组成的 BST，统一增设外部节点 NULL 使 BST 为真二叉树。

树根必为黑色；
外部节点也为黑色；
红节点只能有黑孩子和黑父亲——即红节点不能连续出现、作父子；
外部节点的黑深度相等——其黑祖先的数目相等，亦定义为全树的黑高度，同理，子树的黑高度就是后代中 NULL 的相对黑深度：

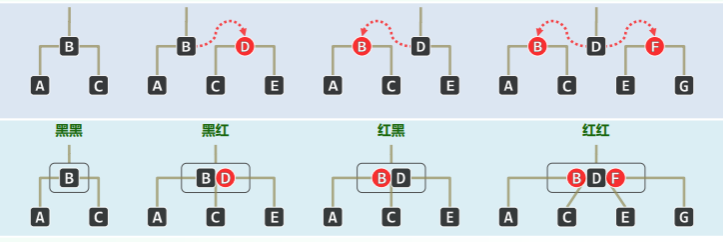
红黑树与 (2,4)-BTree

将红节点抬升至与其黑父亲等高，则每棵红黑树都对应于一棵 (2,4)-BTree：

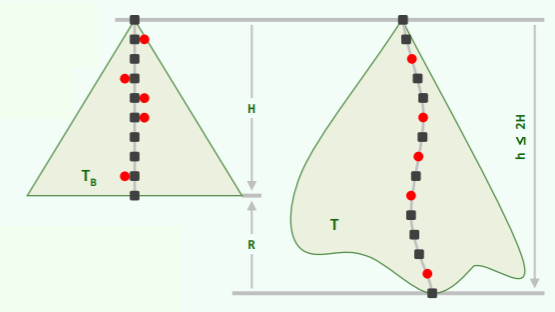
红黑树的高度

包含 n 个内部节点的红黑树 T，高度为 $O (lo g n)$ ——BTree 是平衡的，等价地 Red-black Tree 自然也平衡；
若红黑树 T 的高度为 h，对应红高度为 R，黑高度为 H，则有如下关系：H ⇐ h ⇐ R+H ⇐ 2H；
将红黑树 T 收拢成一棵 B 树 $T_{B}$ ，则红黑树的黑高度是 $T_{B}$ 的高度， $T_{B}$ 的每个超级节点都恰好包含红黑树 T 的一个黑节点；
可以推断得，红黑树的高度 $H \leq ⌊ lo g_{⌈ \frac{4}{2} ⌉} \frac{n + 1}{2} ⌋ + 1 = lo g_{2} (n + 1)$

ADT

template <typename T>
class RedBlack : public BST<T> { //红黑树
public: //BST::search()等其余接口可直接沿用
	BinNodePosi<T> insert( const T & e ); //插入（重写）
	bool remove( const T & e ); //删除（重写）
protected: 
	void solveDoubleRed( BinNodePosi<T> x ); //双红修正
	void solveDoubleBlack( BinNodePosi<T> x ); //双黑修正
	Rank updateHeight( BinNodePosi<T> x ); //更新节点x的高度（重写）
};

#define stature( p ) ( ( p ) ? ( p )->height : 0 ) //外部节点黑高度为0，以上递推

template <typename T> 
int RedBlack<T>::updateHeight( BinNodePosi<T> x ){
	return x->height = IsBlack( x ) + max( stature( x->lc ), stature( x->rc ) ); //只计算黑节点
}

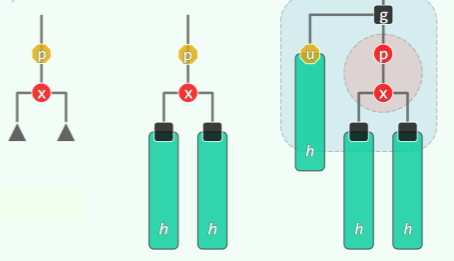
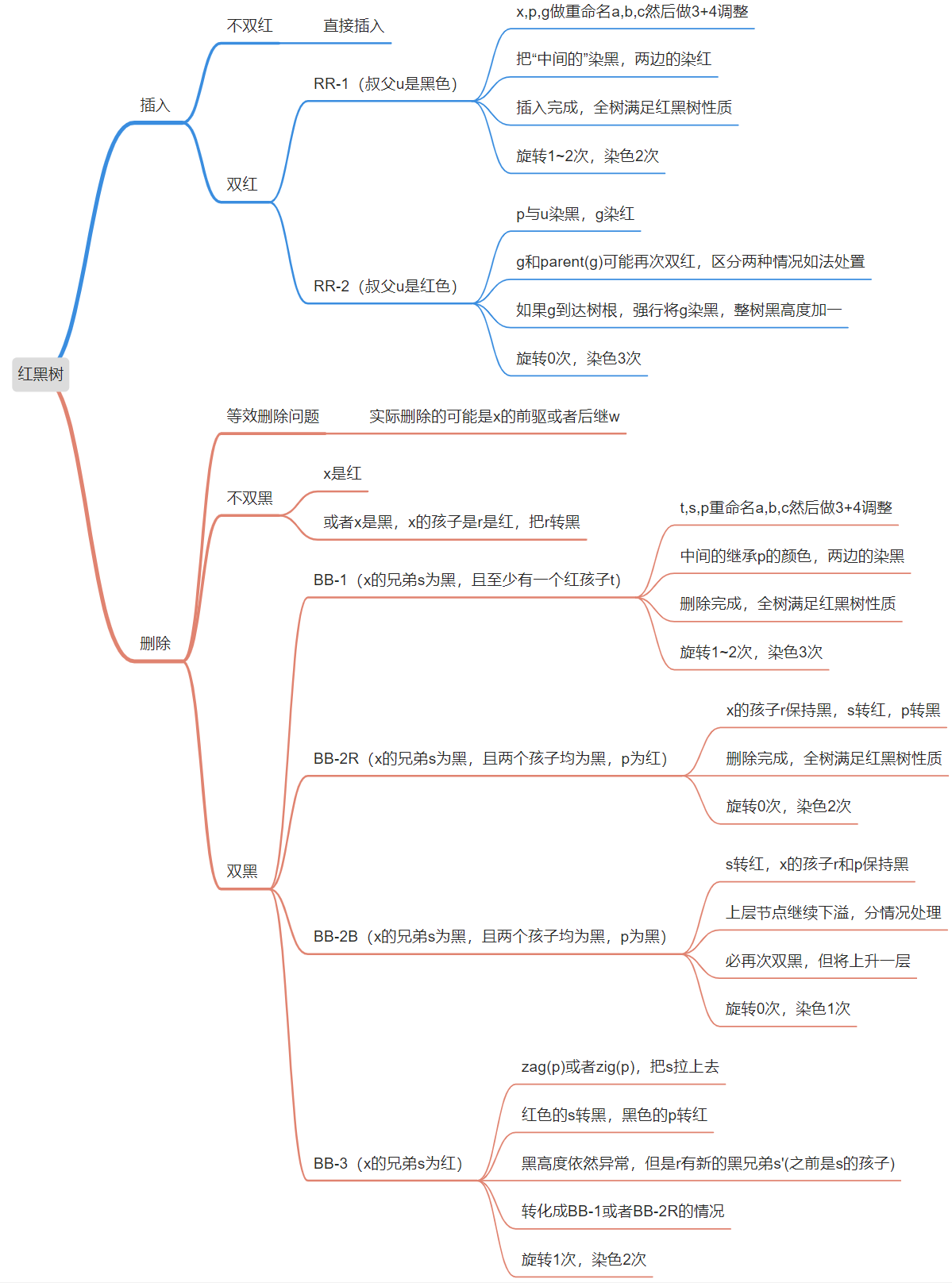
红黑树插入

按 BST 的规则插入关键码 e ：x = insert(e)，常规算法中 x 必为叶节点。

不妨设 x 的父亲 p=x→parent 存在（否则 x 就是根，直接插入就好了），
将 x 染红：x→color = isRoot (x)? B: R;
此时，仍然满足红黑树规则的 1、2、4 规则，但可能出现双红问题：

实现插入

template <typename T> 
BinNodePosi<T> RedBlack<T>::insert( const T & e ) {
	// 确认目标节点不存在（留意对_hot的设置）
	BinNodePosi<T> & x = search( e ); 
	if ( x ) return x;
	
	// 创建红节点x，以_hot为父，黑高度 = 0
	x = new BinNode<T>( e, _hot, NULL, NULL, 0 ); 
	_size++;
	
	// 如有必要，需做双红修正，再返回插入的节点
	BinNodePosi<T> xOld = x; 
	solveDoubleRed( x ); return xOld;
} //无论原树中是否存有e，返回时总有x->data == e

双红修正

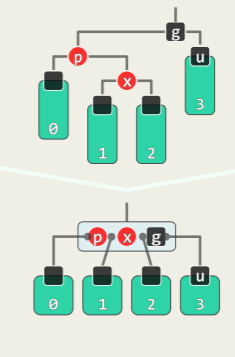
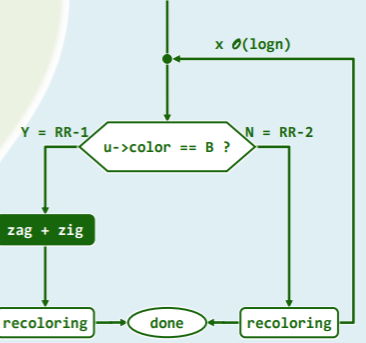
考查祖父 g=p→parent，和叔父 u=uncle (x)=sibling (p)，根据 u 的颜色分别处理：

RR-1: u→color == Black
- 此时，x、p、g 的四个孩子（可能包含外部节点）全为黑且黑高度相同；
- 则进行 3+4 重构，并且将 b 转黑，a 和 c 转红，
- 从 B 树的角度理解，双红冲突的本质就是在三叉节点中插入红关键码后黑关键码不再居中（RRB 或 BRR）——再重新染色即可，此后，调整随即完成：
RR-2: u→color == Red
- 此时对应的 B 树中，等效于超级节点发生上溢，
- 则将 p 与 u 转黑，g 转红，
- 在 B 树中等效于节点分裂、g 上升一层：
- 同样，类似于 B 树的分裂上溢，红黑树如此双红修正可能导致祖父 g 与曾祖父 gg 又出现双红冲突（持续上溢分裂），依法炮制即可，因此可能上升至树根，此时将树根转为黑色——整棵树黑高度+1；

实现双红修正

/**
 * RedBlack双红调整算法：解决节点x与其父均为红色的问题。分为两大类情况：
 *    RR-1：2次颜色翻转，2次黑高度更新，1~2次旋转，不再递归
 *    RR-2：3次颜色翻转，3次黑高度更新，0次旋转，需要递归
 **/
template <typename T> 
void RedBlack<T>::solveDoubleRed( BinNodePosi<T> x ) { // x当前必为红
	if ( IsRoot( *x ) ) {
	//若已（递归）转至树根，则将其转黑，整树黑高度也随之递增
	_root->color = RB_BLACK; 
	_root->height++; return;
	} //否则，x的父亲p必存在
	
	BinNodePosi<T> p = x->parent; if ( IsBlack( p ) ) return; //若p为黑，则可终止调整。否则
	BinNodePosi<T> g = p->parent; //既然p为红，则x的祖父必存在，且必为黑色
	BinNodePosi<T> u = uncle( x ); //以下，视x叔父u的颜色分别处理
	
	if ( IsBlack( u ) ) { // u为黑色（含NULL）时 
	    if ( IsLChild( *x ) == IsLChild( *p ) ) //若x与p同侧（即zIg-zIg或zAg-zAg），则
	        p->color = RB_BLACK; //p由红转黑，x保持红
	    else //若x与p异侧（即zIg-zAg或zAg-zIg），则
	        x->color = RB_BLACK; //x由红转黑，p保持红
	    g->color = RB_RED; //g必定由黑转红
		//以上虽保证总共两次染色，但因增加了判断而得不偿失
		//在旋转后将根置黑、孩子置红，虽需三次染色但效率更高
	    BinNodePosi<T> gg = g->parent; //曾祖父（great-grand parent）
	    BinNodePosi<T> r = FromParentTo( *g ) = rotateAt( x ); //调整后的子树根节点
	    r->parent = gg; //与原曾祖父联接
   } else { //若u为红色
	    p->color = RB_BLACK; p->height++; //p由红转黑
	    u->color = RB_BLACK; u->height++; //u由红转黑
	    g->color = RB_RED; //在B-树中g相当于上交给父节点的关键码，故暂标记为红
	    solveDoubleRed( g ); //继续调整：若已至树根，接下来的递归会将g转黑（尾递归，不难改为迭代）
	}
}

双红修复复杂度分析

重构、染色只需要常数时间，故只需统计总次数：

RedBlack::insert () 只需要 O (logn)时间，期间至多做 O (logn)次重染色、O (1)次旋转
即 RR-2 至多可以出现 O (logn)次，而 RR1 至多出现 1 次，流程图如下：

situation	uncle color	rotate num	recolor	result
RR-1	U.color == Black	1~2	2	调整随即完成
RR-2	U.color == Red	0	3	可能再次导致双红，但势必规模缩小

红黑树删除

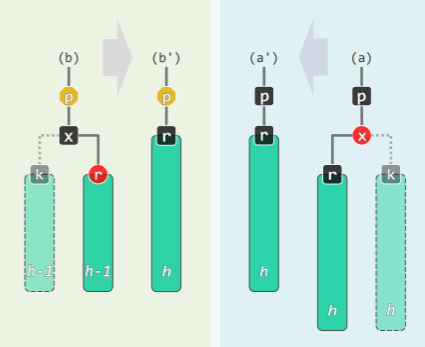
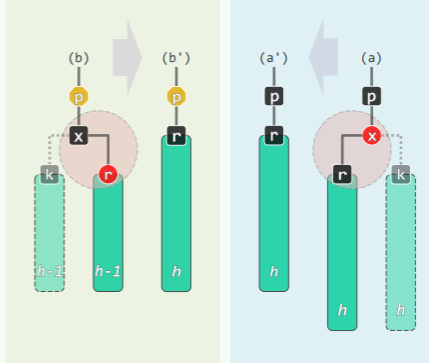
按照 BST 常规算法，执行 r=removeAt (x,_hot)，实际被摘除的可能是 x 的前驱或后继 w，无论如何，不妨统称为 x：

x 由孩子 r 接替，此时另一孩子 k 必定为 NULL；
随后的调整过程中，x 可能逐层上升——故假想地、等效地理解：k 是一棵黑高度与 r 相等的子树且随 x 一并摘除（尽管实际上也未出现过）
完成 removeAt 之后，条件 1、2 满足，条件 3 、4 未必满足；
- 原树中考查 x 与 r，若 x 为红，则条件 3、4 自然满足；
- 若 r 为红，则令其与 x 交换颜色，再用上条操作即可——删除完成！
- 若 x 与 r 均黑，则出现双黑冲突——摘除 x 并代之以 r 后，全树黑深度不再统一，即等价于 B 树中 x 所属节点下溢——需要进行双黑修复

实现删除

template <typename T> 
bool RedBlack<T>::remove( const T& e ) { //从红黑树中删除关键码e
	BinNodePosi<T>& x = search( e ); 
	if ( !x ) return false; //确认目标存在（留意_hot的设置）
	BinNodePosi<T> r = removeAt( x, _hot ); //删除_hot的某个孩子，r指向其接替者
	if ( !( --_size ) ) return true; //若删除后为空树，可直接返回

	if ( !_hot )  {
		//若刚被删除的是根节点，则将其置黑，并更新黑高度
		_root->color = RB_BLACK;
		updateHeight( _root ); 
		return true; 
	}
	// assert: 以下，原x（现r）必非根，_hot必非空
	//若所有祖先的黑深度依然平衡，则无需调整
	if ( BlackHeightUpdated( *_hot ) ) return true; 

	// 至此，必定失衡，若替代节点r为红，则只需简单地反转其颜色
	if ( IsRed( r ) ) { 
		r->color = RB_BLACK; 
		r->height++; 
		return true; 
	}
	// assert: 以下，原x（现r）均为黑色
	solveDoubleBlack( r ); 
	return true; //经双黑调整后返回
} //若目标节点存在且被删除，返回true；否则返回false

双黑修复

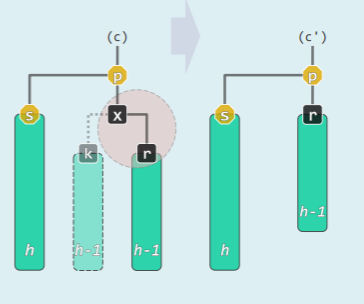
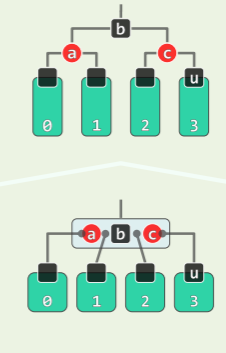
考查 x 的父亲 p 和兄弟 s，分以下四种情况处理：

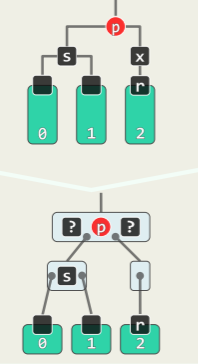
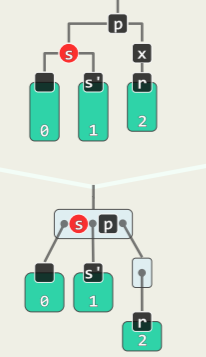
BB-1: s 为黑且至少有一个红孩子t
- 通过 3+4 重构后，r 保持黑色，将 a、c 染黑，b 继承 p 的颜色，此时红黑树的性质在全局恢复，删除完成！
- 等价于通过关键码的旋转，消除超级节点的下溢——对应的 B 树中，p 若为红，其超级节点的两侧必有且仅有一黑；p 若为黑，必自成超级节点：
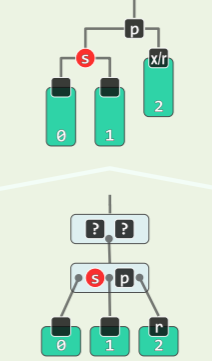
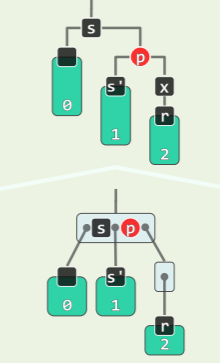
BB-2R: s 为黑，且两个孩子均为黑，p 为红
- r 保持黑，s 转红，p 转黑，红黑树的性质在全局恢复；
- 对应的 B 树中，等效于下溢节点与兄弟合并，此后上层节点不会继续下溢（合并之前，p 的两侧必有一个黑关键码）：
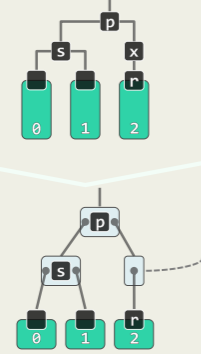
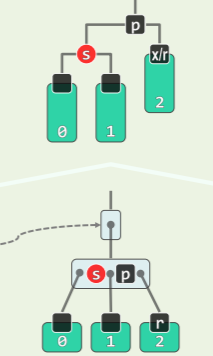
BB-2B：s 为黑，且两个孩子均为黑，p 为黑
- s 转红，r 与 p 保持黑，红黑树的性质在局部恢复；
- 对应的 B 树中，等效于下溢节点与兄弟合并——合并前 p 和 s 均属与单关键码节点，因此孩子的下溢修复后，父节点可能又会下溢，不过最多下溢至根 O (logn)步：
BB-3: s 为红，其余孩子皆为黑
- 绕 p 单旋，s 红转黑，p 黑转红，虽然黑高度仍然异常，但 r 有了一个新的黑兄弟 s’，故能转化为前述情况，并且 p 已经为红，必然情况是 BB-2R 或 BB-1，这样再过一轮调整必然全局恢复红黑树的性质：

实现双黑修复

/**
 * RedBlack双黑调整算法：解决节点x与被其替代的节点均为黑色的问题
 * 分为三大类共四种情况：
 *    BB-1 ：2次颜色翻转，2次黑高度更新，1~2次旋转，不再递归
 *    BB-2R：2次颜色翻转，2次黑高度更新，0次旋转，不再递归
 *    BB-2B：1次颜色翻转，1次黑高度更新，0次旋转，需要递归
 *    BB-3 ：2次颜色翻转，2次黑高度更新，1次旋转，转为BB-1或BB2R
 **/
template <typename T> void RedBlack<T>::solveDoubleBlack( BinNodePosi<T> r ) {
	BinNodePosi<T> p = r ? r->parent : _hot; 
	if ( !p ) return; //确定r的父亲，若父亲不存在，则被删除者x为根节点，平凡情况不必修复

	BinNodePosi<T> s = ( r == p->lc ) ? p->rc : p->lc; //确定r的兄弟
	if ( IsBlack( s ) ) { //兄弟s为黑
	    BinNodePosi<T> t = NULL; //确定s的红孩子（若左、右孩子皆红，左者优先；皆黑时为NULL），根据该结果判断情况
	    if ( IsRed( s->rc ) ) t = s->rc; //右子
	    if ( IsRed( s->lc ) ) t = s->lc; //左子
	    if ( t ) { //黑s有红孩子：BB-1
	        RBColor oldColor = p->color; //备份原子树根节点p颜色，并对t及其父亲、祖父
		    // 以下，通过旋转重平衡，并将新子树的左、右孩子染黑
	        BinNodePosi<T> b = FromParentTo( *p ) = rotateAt( t ); //旋转
	        if ( HasLChild( *b ) ) { 
		        b->lc->color = RB_BLACK;
		        updateHeight( b->lc ); 
			} //左子
	        if ( HasRChild( *b ) ) { 
		        b->rc->color = RB_BLACK; 
		        updateHeight( b->rc ); 
			} //右子
	        b->color = oldColor; 
	        updateHeight( b ); //新子树根节点继承原根节点的颜色
	    } else { //黑s无红孩子
	        s->color = RB_RED; 
	        s->height--; //s转红
	        if ( IsRed( p ) ) { // BB-2R：s孩子均黑，p红
	            p->color = RB_BLACK; //p转黑，但黑高度不变
	        } else { //BB-2B：s孩子均黑，p黑
	            p->height--; //p保持黑，但黑高度下降
	            solveDoubleBlack( p ); //递归上溯
	        }
	    }
	} else { //兄弟s为红：BB-3：s红（双子俱黑）
	    s->color = RB_BLACK; 
	    p->color = RB_RED; //s转黑，p转红
	    
	    BinNodePosi<T> t = IsLChild( *s ) ? s->lc : s->rc; //取t与其父s同侧
	    _hot = p; 
	    FromParentTo( *p ) = rotateAt( t ); //对t及其父亲、祖父做平衡调整
	    solveDoubleBlack( r ); //继续修正r处双黑――此时的p已转红，故后续只能是BB-1或BB-2R
	}
}

双黑修复复杂度分析

删除只需 O (logn)时间，涉及 O (logn)次重染色，O (1)次旋转：

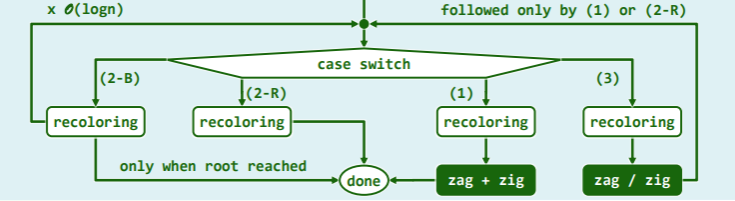
situation	color	rotate	recolor	result
BB-1	s=black, s→child=red	1~2	3	调整随即完成
BB-2R	s=black, p=red	0	2	调整随即完成
BB-2B	s=black, p=black	0	1	必然再次双黑，但下溢情况上升一层
BB-3	s=red	1	2	转为 BB-1 或 BB-2R

kdTree

范围查找

一维

给定直线 L 上的点集 P = { p0, ..., pn-1 }，对于任一区间 R = [x1, x2]，P 中的哪些点落在其中？

蛮力法

遍历点集 P，并逐个地花费 O(1) 时间判断各点是否落在区间 R 内——如此总体运行时间为 Θ(n)。这一效率甚至看起来似乎还不差——毕竟在最坏情况下，的确可能有多达 Ω(n) 个点命中，而直接打印报告也至少需要 Ω(n) 时间。

然而，当我们试图套用以上策略来处理更大规模的输入点集时，就会发现这种方法显得力不从心。实际上，蛮力算法的效率还有很大的提升空间，这一点可从以下角度看出。

首先，当输入点集的规模大到需要借助外部存储器时，遍历整个点集必然引发大量 I/O 操作。此类操作往往是制约算法实际效率提升的最大瓶颈，应尽量予以避免。
另外，当数据点的坐标分布范围较大时，通常的查询所命中的点，在整个输入点集中仅占较低甚至极低的比例。此时，“查询结果的输出需要 Ω(n) 时间”的借口，已难以令人信服。

预处理

在典型的范围查询应用中，输入点集数据与查询区域的特点迥异。

一方面，输入点集 P 通常会在相当长的时间内保持相对固定——数据的这种给出及处理方式，称作批处理（batch）或离线（offline）方式。
同时，对于同一输入点集，往往需要针对大量的随机定义的区间 R，反复地进行查询——数据的这种给出及处理方式，称作在线（online）方式。

因此，只要通过适当的预处理，将输入点集 P 提前整理和组织为某种适当的数据结构，就有可能进一步提高此后各次查询操作的效率。

一维范围查询的有效方法：有序向量

最为简便易行的预处理方法，就是在 O(nlogn)时间内，将点集 P 组织为一个有序向量。如图所示，此后对于任何 R = [x1, x2]，首先利用有序向量的查找算法，在 O(logn) 时间内找到不大于 x2 的最大点 pt。然后从 pt 出发，自右向左地遍历向量中的各点，直至第一个离开查询区间的点 ps。其间经过的所有点，既然均属于区间范围，故可直接输出。

如此，在每一次查询中，pt 的定位需要 O(logn)时间。若接下来的遍历总共报告出 r 个点，则总体的查询时间成本为 O(r + logn)。

请注意，此处估计时间复杂度的方法，不免有点特别。这里，需要同时根据问题的输入规模和输出规模进行估计。一般地，时间复杂度可以这种形式给出的算法，也称作输出敏感的（output sensitive）算法。从以上实例可以看出，与此前较为粗略的最坏情况估计法相比，这种估计方法可以更加准确和客观地反映算法的实际效率。

二维：平面范围查找

难点和挑战在于，在实际应用中，往往还需要同时对多个维度做范围查找。以人事数据库为例，诸如“年龄介于某个区间，而且工资介于某个区间”之类的组合查询十分普遍。如图8.36所示，若将年龄与工资分别表示为两个正交维度，则人事数据库中的记录，将对应于二维平面上（第一象限内）的点。于是相应地，这类查询都可以抽象为在二维平面上，针对某一相对固定的点集的范围查询，其查询范围可描述为矩形 R = [x1, x2] ✖ [y1, y2]。很遗憾，上述基于二分查找的方法并不能直接推广至二维情况，更不用说更高维的情况了，因此必须另辟蹊径，尝试其它策略。

其一就是马鞍查找法： 2-22 马鞍查找——二维向量查找；
其二是 kd-tree 法；

BBST 解决一维范围查找的思路

先回到一维范围查找的问题，并尝试其它可以推广至二维甚至更高维版本的方法。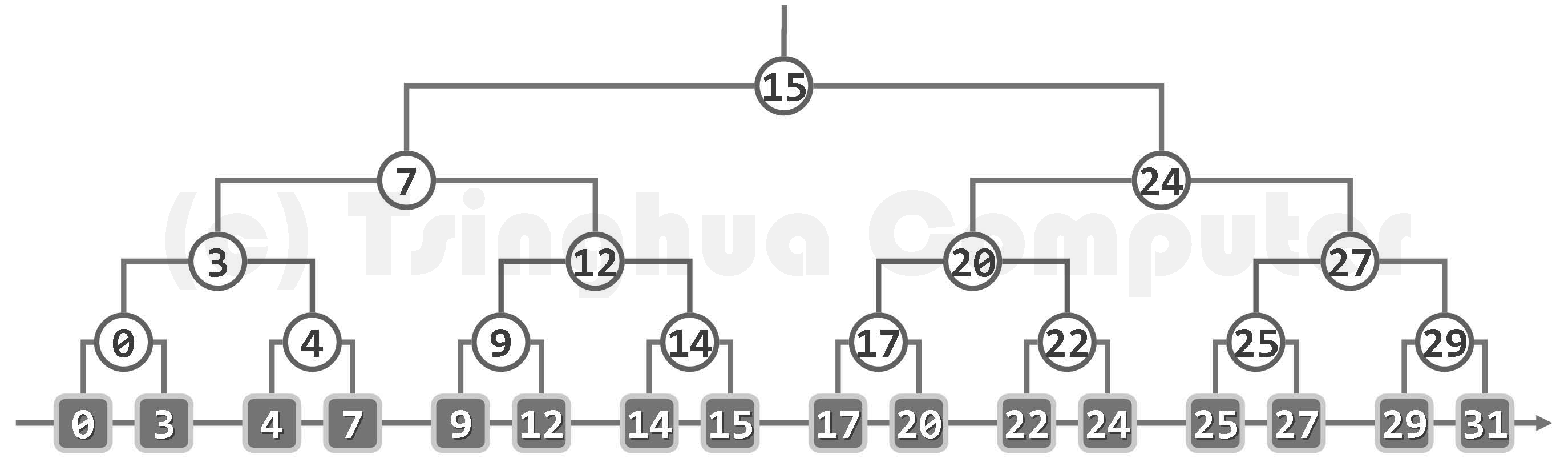在 O(nlogn)时间内，将输出点集组织并转化为如图所示的一棵平衡二叉搜索树。

请注意，其中各节点的关键码可能重复。不过，如此并不致于增加渐进的空间和时间复杂度：

每个关键码至多重复一次，总体依然只需 O (n)空间；
尽管相对于常规二叉搜索树多出一层，但树高依然是 O (logn)。

如此在空间上所做的些许牺牲，可以换来足够大的收益：查找的过程中，在每一节点处，至多只需做一次（而不是两次）关键码的比较。当然另一方面，无论成功与否，每次查找因此都必然终止于叶节点——不小于目标关键码的最小叶节点。不难验证，就接口和功能而言，此类形式二叉搜索树，完全对应于和等价于二分查找算法的版本 C。

查询算法

继续上例，如图所示，设查询区间为 [1, 23]。

首先，在树中分别查找这一区间的左、右端点 1 和 23，并分别终止于叶节点 3 和 24。
接下来，考查这两个叶节点共同祖先中的最低者，即所谓的最低共同祖先（lowest common ancestor, LCA），具体地亦即 lca (3, 24) = 15
然后，从这一共同祖先节点出发，分别重走一遍通往节点 3 和 24 的路径（分别记作 path (3) 和 path (24)）。在沿着 path (3)/path (24)下行的过程中，忽略所有的右转/左转；而对于每一次左转/右转，都需要遍历对应的右子树/左子树（图中以阴影示意），并将其中的叶节点悉数报告出来。

就本例而言，沿 path(3)被报告出来的叶节点子集，依次为： { 9, 12, 14, 15 }、{ 4, 7 }、{ 3 }

沿 path(24)被报告出来的叶节点子集，依次为： { 17, 20 }、{ 22 }

正确性和效率

不难看出，如此分批报告出来的各组节点，都属于查询输出结果的一部分，且它们相互没有重叠。另一方面，除了右侧路径的终点 24 需要单独地判断一次，其余的各点都必然落在查询范围以外。因此，该算法所报告的所有点，恰好就是所需的查询结果。

在每一次查询过程中，针对左、右端点的两次查找及其路径的重走，各自不过 O(logn)时间（实际上，这些操作还可进一步合并精简）。在树中的每一层次上，两条路径各自至多报告一棵子树，故累计不过 O(logn)棵。幸运的是，根据 习题[5-11] (其实就是树的遍历算法的时间复杂度为 O(n)) 的结论，为枚举出这些子树中的点，对它们的遍历累计不超过 O(r)的时间，其中 r 为实际报告的点数。

综合以上分析，每次查询都可在 O(r + logn)时间内完成。该查询算法的运行时间也与输出规模相关，故同样属于输出敏感的算法。新算法的效率尽管并不高于基于有序向量的算法，却可以便捷地推广至二维甚至更高维。

kdTree

循着上一节采用平衡二叉搜索树实现一维查询的构思，可以将待查询的二维点集组织为所谓的 kd-树（kd-tree）结构。在任何的维度下，kd-树都是一棵递归定义的平衡二叉搜索树。

[! note] kdtree 由J. L. Bentley 于 1975 年发明，其名字来源于“k-dimensional tree”的缩写¹

适用于任意指定维度的欧氏空间，并视具体维度，相应地分别称作 2d-树、3d-树、…，等

故上节所介绍的一维平衡二叉搜索树，也可称作1d-树

以下不妨以二维情况为例，就2d-树的原理以及构造和查询算法做一介绍。

节点及其矩形区域

具体地，2d-树中的每个节点，都对应于二维平面上的某一矩形区域，且其边界都与坐标轴平行。当然，有些矩形的面积可能无限。

后面将会看到，同层节点各自对应的矩形区域，经合并之后恰好能够覆盖整个平面，同时其间又不得有任何交叠。因此，不妨如图8.39所示统一约定，每个矩形区域的左边和底边开放，右边和顶边封闭。

构造算法

作为以上条件的特例，树根自然对应于整个平面。一般地如上图所示，若 P 为输入点集与树中当前节点所对应矩形区域的交集（即落在其中的所有点），则可递归地将该矩形区域切分为两个子矩形区域，且各包含 P 中的一半的点。

若当前节点深度为偶（奇）数，则沿垂直（水平）方向切分，所得子区域随同包含的输入点分别构成左、右孩子。如此不断，直至子区域仅含单个输入点。每次切分都在中位点（median point）——按对应的坐标排序居中者——处进行，以保证全树高度不超过 O(logn)。

具体地，2d-树的整个构造过程，可形式化地递归描述如算法所示。

KdTree* buildKdTree(P, d) { //在深度为d的层次，构造一棵对应于（子）集合P的（子）2d-树
	if (P == {p}) return CreateLeaf(p); //递归基
	root = CreateKdNode(); //创建（子）树根
	root->splitDirection = Even(d) ? VERTICAL : HORIZONTAL; //确定划分方向
	root->splitLine = FindMedian(root->splitDirection, P); //确定中位点
	(P1, P2) = Divide(P, root->splitDirection, root->splitLine); //子集划分
	root->lc = buildKdTree(P1, d + 1); //在深度为d + 1的层次，递归构造左子树
	root->rc = buildKdTree(P2, d + 1); //在深度为d + 1的层次，递归构造右子树
	return root; //返回（子）树根
}

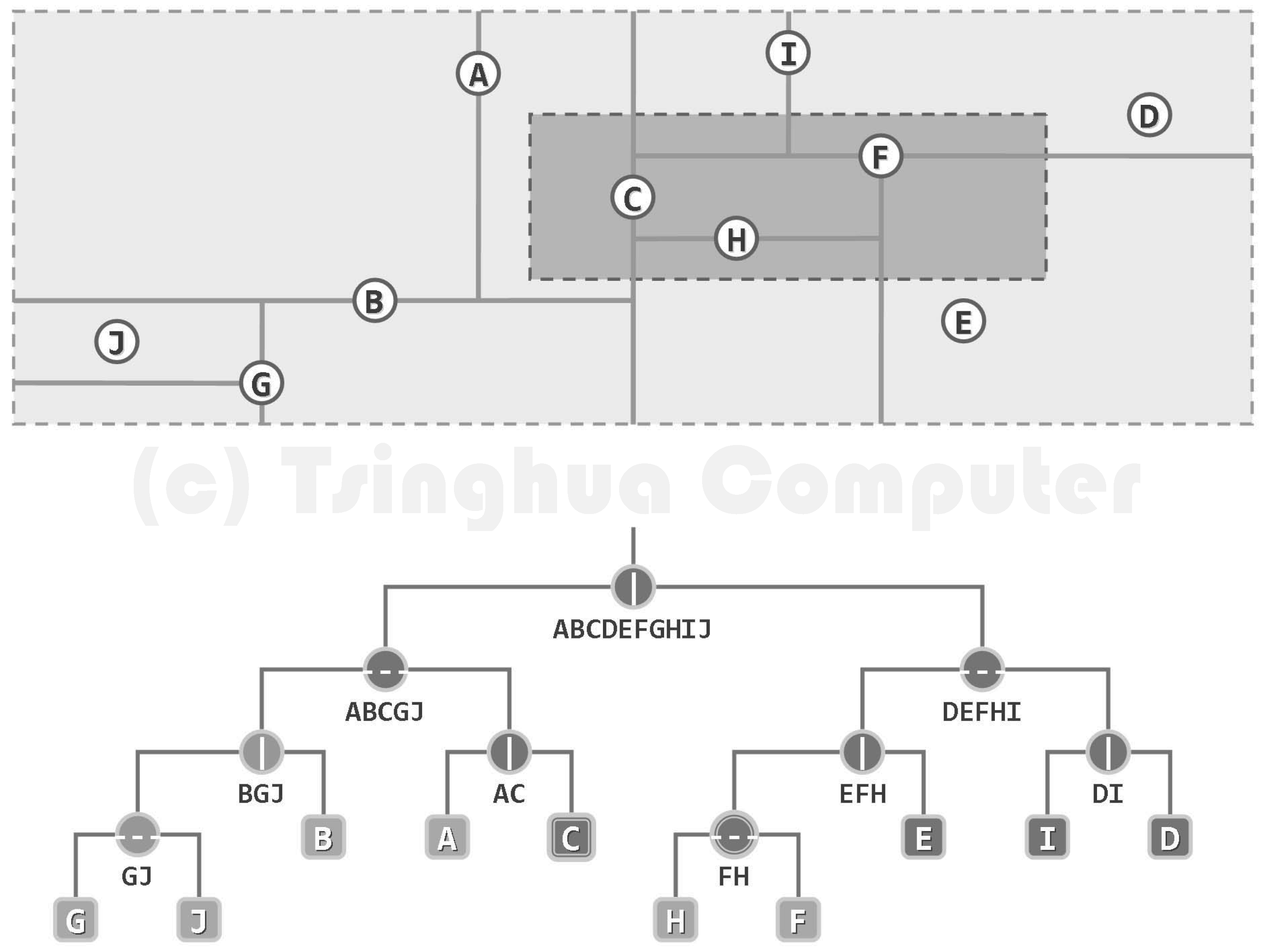
实例

首先创建树根节点，并指派以整个平面以及全部 7 个输入点。
第一轮切分如图 (b)所示。以水平方向的中位点 C 为界，将整个平面分作左、右两半，点集 P 也相应地被划分为子集{ A, B, C, G }和{ D, E, F }，它们随同对应的半平面，被分别指派给深度为 1 的两个节点。
第二轮切分如图 (c)所示。对于左半平面及其对应的子集{ A, B, C, G }，以垂直方向的中位点 B 为界，将其分为上、下两半，并分别随同子集{B, G}和{A, C}，指派给深度为 2 的一对节点；对于右半平面及其对应的子集{ D, E, F }，以垂直方向的中位点 F 为界，将其分为上、下两半，并分别随同子集{ E, F }和{ D }，指派给深度为 2 的另一对节点。
最后一轮切分如图 (d)所示。对树中仍含有至少两个输入点的三个深度为 2 的节点，分别沿其各自水平方向的中位点，将它们分为左、右两半，并随同对应的子集分配给三对深度为 3 的节点。

至此，所有叶节点均只包含单个输入点，对平面的整个划分过程遂告完成，同时与原输入点集 P 对应的一棵2d-树也构造完毕。

基于 2d-tree 的范围查询

思路

经过如上预处理，将待查询点集 P 转化为一棵2d-树之后，对于任一矩形查询区域 R，范围查询的过程均从树根节点出发，按如下方式递归进行。因为不致歧义，以下叙述将不再严格区分2d-树节点及其对应的矩形子区域和输入点子集。

在任一节点 v 处，若子树 v 仅含单个节点，则意味着矩形区域 v 中仅覆盖单个输入点，此时可直接判断该点是否落在 R 内。否则，不妨假定矩形区域 v 中包含多个输入点。
此时，视矩形区域 v 与查询区域 R 的相对位置，无非三种情况：
- 情况 A：若矩形区域 v 完全包含于 R 内，则其中所有的输入点亦均落在 R 内，于是只需遍历一趟子树 v，即可报告这部分输入点。
- 情况 B：若二者相交，则有必要分别深入到 v 的左、右子树中，继续递归地查询。
- 情况 C：若二者彼此分离，则子集 v 中的点不可能落在 R 内，对应的递归分支至此即可终止。

算法

kdSearch(v, R) { //在以v为根节点的(子)2d-树中，针对矩形区域R做范围查询
	if (isLeaf(v) //若抵达叶节点，则
	{ if (inside(v, R)) report(v); return; } //直接判断并终止递归

	if (region(v->lc) in R != nothing) //情况A：若左子树完全包含域R内，则直接遍历
		reportSubtree(v->lc);
	else if (region(v->lc) and R) //情况B：若左子树对应的矩形与R相交，则递归查询
		kdSearch(v->lc, R);

	if (region(v->rc)  R) //情况A：若右子树完全包含于R内，则直接遍历
		reportSubtree(v->rc);
	else if (region(v->rc) and R != nothing) //情况B：若右子树对应的矩形不与相交，则递归查询
		kdSearch(v->rc, R);
}

可见，递归只发生于情况 B；对于其余两种情况，递归都会随即终止。特别地，情况 C 只需直接返回，故在算法中并无与之对应的显式语句。

实例

考查图中的 2d- 树，设采用 kdSearch()算法，对阴影区域进行查询。不难验证，递归调用仅发生于黑色节点（情况 B）；而在灰色节点处，并未发生递归调用（情况 C 或父节点属情况 A）。

命中的节点共分两组：{ C }作为叶节点经直接判断后确定；{ F, H }则因其所对应区域完全包含于查询区域内部（情况 A），经遍历悉数输出（习题8-17）。

正确性及复杂度

由上可见，凡被忽略的子树，其对应的矩形区域均完全落在查询区域之外，故该算法不致漏报。反之，凡被报告的子树，其对应的矩形区域均完全包含在查询区域以内（且互不相交），故亦不致误报。

平面范围查询与一维情况不同，在同一深度上可能递归两次以上，并报告出多于两棵子树。但更精细的分析（习题8-16）表明，被报告的子树总共不超过 $O (n)$ 棵，累计耗时 $O (n)$ 。

J. L. Bentley. Multidimensional Binary Search Trees Used for Associative Searching. Communications of the ACM (1975), 18(9):509-517 ↩

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索

61-Balanced-BST

AVL Tree

平衡因子

高度与节点数

失衡与复平衡

插入

删除

3+4 重构

性能分析

Splay Tree

局部性

双层伸展

zig-zag/zag-zig

zig-zig/zag-zag

zig/zag

伸展实现

查找

插入

删除

性能分析

势能分摊分析

势能定义

调整时间的上界

B-Tree

背景

特点

准确定义

举例

ADT

查找

性能

树高

插入

分裂

Insert-Example

上溢修复

删除

举例

Case III - shrink height

下溢修复

Red-black Tree

动机

并发性

持久性

红黑树的规则

红黑树与 (2,4)-BTree

红黑树的高度

ADT

红黑树插入

实现插入

双红修正

实现双红修正

双红修复复杂度分析

红黑树删除

实现删除

双黑修复

实现双黑修复

双黑修复复杂度分析

kdTree

范围查找

一维

蛮力法

预处理

一维范围查询的有效方法：有序向量

二维：平面范围查找

BBST 解决一维范围查找的思路

查询算法

正确性和效率

kdTree

节点及其矩形区域

构造算法

实例

基于 2d-tree 的范围查询

思路