20-Learning-to-Answer-Y-N

Perceptron Hypothesis Set

Formulate in Linear Algebra

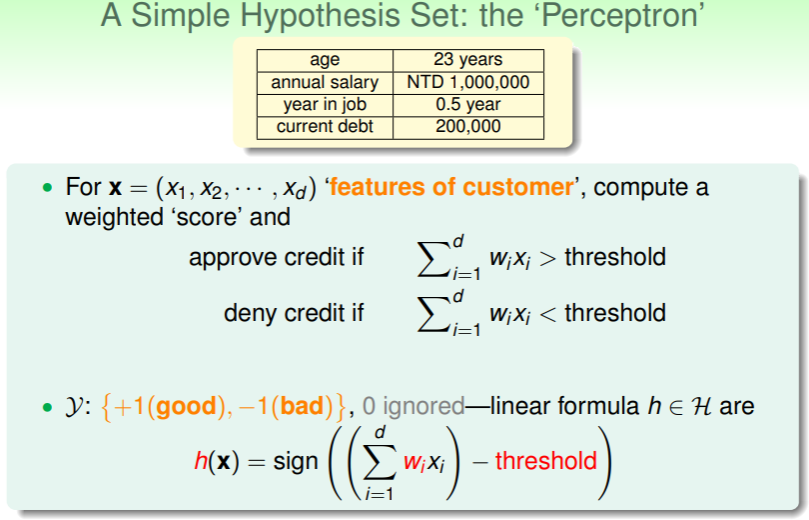
• 每个客户的数据都组成一个向量 $\mathbf{x}=(x_1,x_2,...,x_n)$ ，其中的每一个分量 $x_i$ 即是客户的特征，如年龄、年薪、工龄、负债情况…
• 对每一个分量 $x_i$ 赋以权重 $w_i$，二者相乘后求和，即可得到该客户的特征——从而验证能否通过批准信用卡的阈值 threshold ，
• 对客户特征与阈值 threshold 取差值，差值为正即允许批准信用卡的申请，为负则不批准，若是为 0 ？事实上，这种情况很少见，剔除后也不会造成影响；

对以上符号和想法用线性代数中的运算表示，如下：

• 假设 $h$ 对样本数据 $\mathbf{x}$ 的关系式：
• 这里为了将 threshold 纳入向量运算中，延伸一个第 0 维的分量 $w_0$ 和 $x_0$ 。

Linear Classifier

进一步地，这个假设函数 $h(\mathbf{x})$ 可否图形化？

• 
• 若只取两个分量 $\mathbf{x}=(x_0,x_1,x_2)$ ，即得到二维空间 ${\mathbb{R}}^2$（取更多分量则得到更高维的图形 ${\mathbb{R}}^n$），
• 对用户样本的判断称作加标签（label），+1 记作蓝色圆圈，-1 记作红色叉，
• 用户的特征向量和对应标签即是这个二维空间中的一个点 $({\mathbf{x}}_i,y_i)$ ，
• 假设函数 $h(\mathbf{x})$ 在二维空间中的图形就是一个直线，对直线两侧的点进行预测，一侧为正，一侧为负，
• 这就是线性分类器；

练习：判断垃圾邮件可以哪些维度？

Perceptron Learning Algorithm

所谓 PLA ，即是在假设集 $\mathcal{H}$ 中选择出对目标函数 f 的最佳估计 g 的过程。

Choose Right Hypothesis

现在的问题就是如何从无穷大的 $\mathcal{H}$ 中尽可能高效地取出尽可能准确的 g 作为 f 的估计：

• f 是未知的，$\mathcal{H}$ 的空间又是无穷大的，因此取出准确的 g 相当困难，
• 目标是找出理想的 g ，使得 $g({\mathbf{x}}_n)=f({\mathbf{x}}_n)=y_n$ ，
• 一个好的方法是，先任意地选择一个 g 作为起始，然后根据数据样本逐步地修正使用它发生的错误，直到发生错误的概率足够小——起始的估计称为 $g_0$ ，其有权重向量 $(w_0,w_1,w_2,...,w_N)$，因此简化地将起始估计取其权重向量，并记作 ${\mathbf{w}}_0$ 。

Correct the Known Mistakes

现在，从 ${\mathbf{w}}_0$（可以随意设置权重，比如全为 0）开始，逐步地修正它：

• 
• 如果 ${\mathbf{w}}_0$ 并不是当前数据集中一个完美的估计，那么就一定存在一个样本 $({\mathbf{x}}_{n(t)},y_{n(t)})$ 能够使对其预测的结果和真实的标签并不相同：$\text{sign}\left({\mathbf{w}}_t^T{\mathbf{x}}_{n(t)}\right)\ne y_{n(t)}$ ➡ 这就是“犯错”
• 如何“修正错误”？如果实际的 label 是+1，但是预测却是 -1，那就在预测的权重向量 ${\mathbf{w}}_0$ 上加一个 $y\mathbf{x}$ ，这里 y 是+1；反之亦然
• 那么每一轮 t 都进行这样的错误点查找、纠正，直到越来越接近正确值、不再预测错误，那么最后一轮的这个 ${\mathbf{w}}_{PLA}$ 就是在训练集中最佳的 g .

PLA 的过程是周期性的：

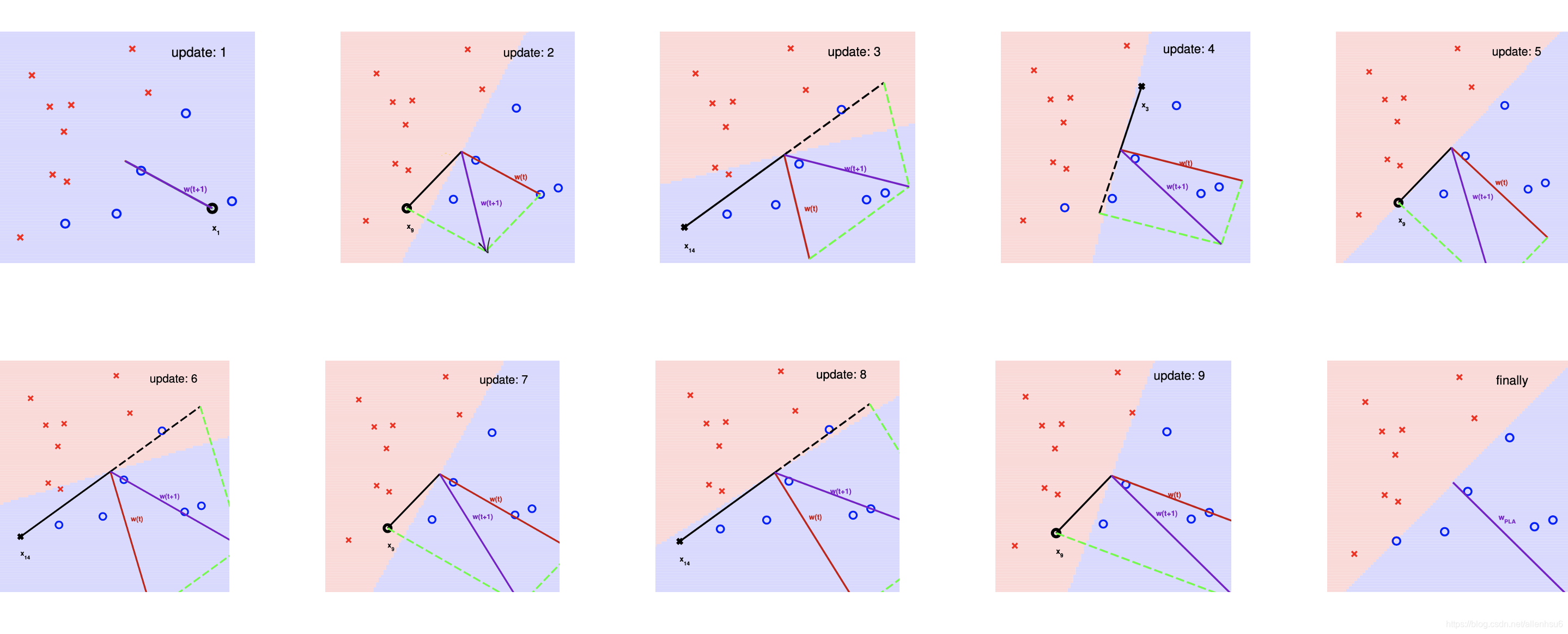
下图是一个 PLA 计算过程的示例：

• 

练习：思考迭代的真实含义

• 这个练习题能够进一步理解每轮迭代都进行了怎样的工作——第三个选项代表了下一轮的分数更大，超出阈值更多，也更有可信度。

Linear Separability

Further Thinking

尽管这样确实能够找到一个 $g\approx f$ ，但仍有几个问题值得思量：

1. 一共要进行多少个周期？—— 解答
2. 这个循环是无限的吗？可否确定会停止？（停止，意即在训练集上的判断不再出错）—— 解答
3. 得到的 g 确实能够代表 f 吗？—— 解答

线性可分性：如果 PLA 能够停止，当且仅当训练集 $\mathcal{D}$ 能够被某个权重 $\mathbf{w}$ 划分且（在训练集上）不再出错，并且由于数据样本的各维分量是一阶的，因此对分类器图形化的话会得到一个线性的分类器：

• 下图左边是线性可分的，中间和右边不是线性可分的：
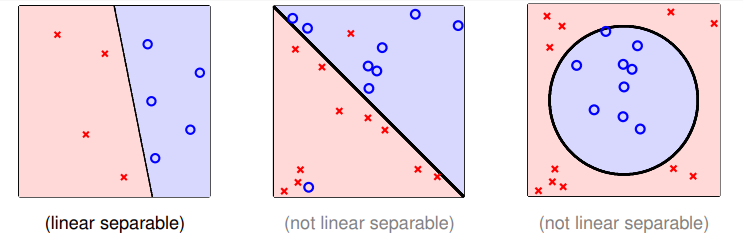
• 对第 2 个问题——只有训练集满足线性可分，才能够确保 PLA 最终能够停止。

Guarantee of PLA

PLA Fact

• PLA 的过程就是 当前轮次的权重 ${\mathbf{w}}_t$ 越来越接近 目标函数的权重 ${\mathbf{w}}_f$ 的过程，
• 而训练集 $\mathcal{D}$ 的线性可分性能够保证，一定存在完美的 ${\mathbf{w}}_f$ 使得对所有训练集中样本的估计 $y_n=\text{sign}({\mathbf{w}}_f^T{\mathbf{x}}_n)$ 成立，
• 另外，PLA 关键在于遇错更新，这也导致 ${\mathbf{w}}_t$ 的增长并不会太快，即不会线性地、成倍数的增加。

基于目标函数的定义可以导出如下的数学关系：${\mathbf{w}}_f$ 对所有的 ${\mathbf{x}}_n$ 的判断都是正确的，即所有样本点都与划分直线有距离（不在直线上）：

$$y_{n(t)}{\mathbf{w}}_f^T{\mathbf{x}}_{n(t)}\ge \underset{n}{\min }\{y_n{\mathbf{w}}_f^T{\mathbf{x}}_n\}>0\text{\hspace{1em}(*)}$$

• 这里 ${\mathbf{w}}_f^T{\mathbf{x}}_n$ 指的就是样本点距离划分直线的带正负号距离，而正确的估计就是 正距离*(+1)，负距离*(-1)，因此总体上总是正的；
• 而 $y_{n(t)}{\mathbf{w}}_f^T{\mathbf{x}}_{n(t)}$ 是 PLA 每一轮迭代时选择的错误点的距离；

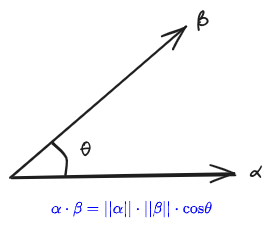
每一轮更新样本点 $({\mathbf{x}}_{n(t)},y_{n(t)})$ 时，实际上就是做这样的运算：${\mathbf{w}}_f^T{\mathbf{w}}_{t+1}={\mathbf{w}}_f^T({\mathbf{w}}_t+y_n{\mathbf{x}}_{n(t)})$，将右项展开，前一项 ${\mathbf{w}}_f^T{\mathbf{w}}_t$ 没有意义，后一项才是关键——由 不等式(*) 可知：

$$\begin{array}{rl}{\mathbf{w}}_f^T{\mathbf{w}}_{t+1}& \ge {\mathbf{w}}_f^T{\mathbf{w}}_t+\underset{n}{\min }\{y_n{\mathbf{w}}_f^T{\mathbf{x}}_n\}\\ & >{\mathbf{w}}_f^T{\mathbf{w}}_t+0\end{array}\text{\hspace{1em}(1)}$$

这个式子说明，每一轮迭代，向量内积都在逐渐增大，意味着两个向量越来越接近，即 ${\mathbf{w}}_t$ 越来越接近 ${\mathbf{w}}_f$ —— 这个说法其实有些片面，因为内积增大不仅可能是方向上越来越接近，也可能是向量长度的成比例变化。

要证伪后者，则需要回顾到 PLA 的最关键性质：遇错更新。所谓遇错，即是 $\text{sign}({\mathbf{w}}_t^T{\mathbf{x}}_{n(t)})\ne y_{n(t)}\iff y_{n(t)}{\mathbf{w}}_t^T{\mathbf{x}}_{n(t)}\le 0$ ，而考查向量的长度：

$$\begin{array}{rl}||{\mathbf{w}}_{t+1}|{|}^2& =||{\mathbf{w}}_t+y_{n(t)}{\mathbf{x}}_{n(t)}|{|}^2\\ & =||{\mathbf{w}}_t|{|}^2+2y_{n(t)}{\mathbf{w}}_t^T{\mathbf{x}}_{n(t)}+||y_{n(t)}{\mathbf{x}}_{n(t)}|{|}^2\\ & \le ||{\mathbf{w}}_t|{|}^2+0+||y_{n(t)}{\mathbf{x}}_{n(t)}|{|}^2\\ & \le ||{\mathbf{w}}_t|{|}^2+\underset{n}{\max }||y_n{\mathbf{x}}_n|{|}^2=||{\mathbf{w}}_t|{|}^2+\underset{n}{\max }||{\mathbf{x}}_n|{|}^2\end{array}\text{\hspace{1em}(2)}$$

• 其中之所以是小于等于，是因为错误会导致 $y_{n(t)}{\mathbf{w}}_t^T{\mathbf{x}}_{n(t)}\le 0$，而最后一行 $y_n$ 的取值不外乎+1 或-1，因此平方后都可以舍去；
• 这也就表明，由于只有犯错才会更新，而犯错同时也限制了增长速度，即不会比上一轮的 ${\mathbf{w}}_t$ 超过 $\underset{n}{\max }||y_n{\mathbf{x}}_n|{|}^2$ ，那么这里的含义就是最多增长最“长”的 ${\mathbf{x}}_n$ 的距离；

联立 (1), (2) 式，可以得知，从 ${\mathbf{w}}_0=0$ 开始迭代，经过 T 次犯错，有这样的关系： $\frac{{\mathbf{w}}_f^T}{||{\mathbf{w}}_f||}\frac{{\mathbf{w}}_T}{||{\mathbf{w}}_T||}\ge \sqrt{T}\cdot \text{constant}=\sqrt{T}\cdot \frac{\min \{y_n{\mathbf{w}}_f^T{\mathbf{x}}_n\}}{||{\mathbf{w}}_f||\max ||{\mathbf{x}}_n||}$

• 这里左边是两个单位长度的向量内积，确实表现了它们角度有多么靠近，靠近的速度就是中式中的 constant 的值。
  • 
• 可能无限靠近吗？不会，单位向量的内积最大长度也不过是 1，因此总会停止下来。

constant 具体是如何推导的呢？

(1)式的放缩：

$$\begin{array}{rl}{\mathbf{w}}_f^T{\mathbf{w}}_{t+1}& \ge {\mathbf{w}}_f^T{\mathbf{w}}_t+\underset{n}{\min }\{y_n{\mathbf{w}}_f^T{\mathbf{x}}_n\}\\ & \ge {\mathbf{w}}_f^T{\mathbf{w}}_{t-1}+2\underset{n}{\min }\{y_n{\mathbf{w}}_f^T{\mathbf{x}}_n\}\\ & ...\\ & \ge {\mathbf{w}}_f^T{\mathbf{w}}_0+(t+1)\underset{n}{\min }\{y_n{\mathbf{w}}_f^T{\mathbf{x}}_n\}=0+(t+1)\underset{n}{\min }\{y_n{\mathbf{w}}_f^T{\mathbf{x}}_n\}\end{array}$$

(2)式的放缩：

$$\begin{array}{rl}||{\mathbf{w}}_{t+1}|{|}^2& \le ||{\mathbf{w}}_t|{|}^2+\underset{n}{\max }||{\mathbf{x}}_n|{|}^2\\ & \le ||{\mathbf{w}}_{t-1}|{|}^2+2\underset{n}{\max }||{\mathbf{x}}_n|{|}^2\\ & ...\\ & \le ||{\mathbf{w}}_0|{|}^2+(t+1)\underset{n}{\max }||{\mathbf{x}}_n|{|}^2=0+(t+1)\underset{n}{\max }||{\mathbf{x}}_n|{|}^2\end{array}$$

练习：理解迭代次数 T 的上界

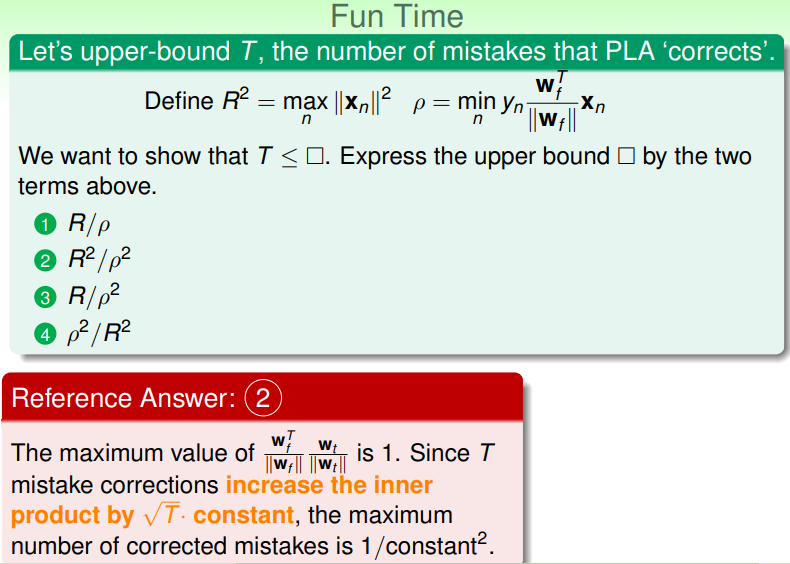
• 这个计算很简单，只需要把之前那个式子中的 constant 移到另一边后两边同时平方一下，即可得出；
• 但这里 $R^2$ 和 $\rho$ 的含义是什么？
  • 前者是向量最大长度的平方，这个最大长度又称为半径；
  • 后者是目标划分直线的法向量与每个样本点的向量的内积的最小值；

ρ 可以提前确定吗？

很遗憾，尽管我们能够得出以上的数学关系式，但 $\rho$ 的具体数值仍由 ${\mathbf{w}}_f$ 向量所确定，因此只能确定 PLA 最终会停下来，但具体的次数在实际运行结束前是无法确定的。

Non-Separable Data

由前文论证可知，如果训练集 $\mathcal{D}$ 确实是线性可分的，并且是遇错更新的，那么必然有以下结论：

• 目标 ${\mathbf{w}}_f$ 和当前迭代轮次 ${\mathbf{w}}_t$ 的内积会快速地增加，即二者角度快速接近；而 ${\mathbf{w}}_t$ 又是遇错更新的，因此增长速度极慢；
• PLA 得到的“直线”必然越来越接近于 ${\mathbf{w}}_f$ 所对应的直线，直到最后停下来。

这样的 PLA 确实易于实现、高效、且对任意维度的向量 $\mathbf{w}$ 都能实现（二维乃至一百维，对程序来说并没有实质的差别）。那么，PLA 真的如此完美吗？显然不是：

1. 我们在实际运行前，是不知道 $\mathcal{D}$ 究竟是不是线性可分的；
2. 我们也不知道究竟要运行多久才会停下来，因为 $\rho$ 是取决于 ${\mathbf{w}}_f$ 的——甚至一旦不是线性可分的，比如有噪音点或非线性可分区域，将无法停止。
   • 对于非线性可分区域，我们可以改进模型解决，后续学习将会解决这个问题，
   • 现在我们先来处理噪音点：

Learning with Noisy Data

当 $\mathcal{D}$ 中掺入噪音：

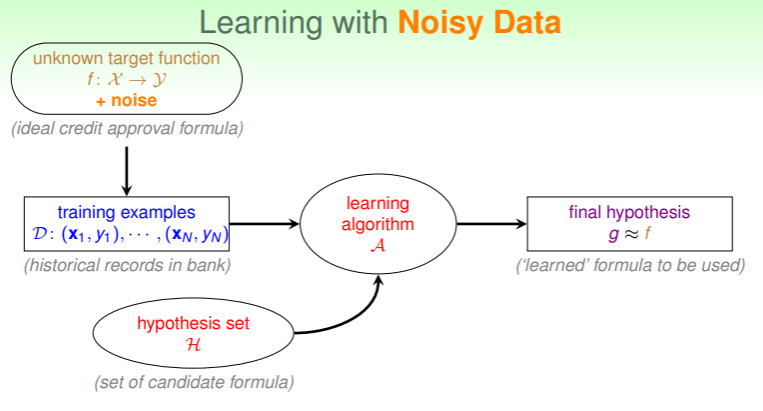
假设一个前提：噪音相对于可信数据是少量的（否则说明数据集不具有可信度）。

• 因此，即使对理想的 f ，也有可能犯错，但大多数情况下 $y_n=f({\mathbf{x}}_n)$ 还是成立的。
• 因此我们在运行中获得的 g ，对 $y_n=g({\mathbf{x}}_n)$ 也是大多数情况下成立的，那么选中一个 g ，使得 ${\mathbf{w}}_g\leftarrow \text{arg}\left(\underset{\mathbf{w}}{\min }\sum _{n=1}^N[y_n\ne \text{sign}({\mathbf{w}}^T{\mathbf{x}}_n)]\right)$ ，即取犯错最少的那个 g 作为估计，不是就能满足要求吗？
• 确实，但不幸的是，选择犯错最少的 g 的算法目前还是个 NP-hard 问题，即不存在多项式（polynomial）时间复杂度内解决的算法，它是 $\mathcal{O}(2^n)$ 复杂度的。

如何解决？捡西瓜丢芝麻策略！（英语中通常称为 Pocket Algorithm）—— 保持最佳的 ${\mathbf{w}}_t$ 在手中，如果下一轮 ${\mathbf{w}}_{t+1}$ 的结果反而导致正确率下降，那么就舍弃之：

练习：Pocket 与 PLA 孰优？

在确实线性可分的 $\mathcal{D}$ 中分别运行 Pokcet 策略和 PLA，孰优？

• Pocket 策略由于每轮都要评估是否有所进步，因此耗时比 PLA 更久；