50-Kernel-Logistic-Regression

Soft-Margin SVM as Regularized Model

继续下文之前回顾一下之前所学的 hard-margin SVM 和 soft-margin SVM 及其对偶问题：

• 
• 在实际使用中我们通常使用 soft-margin SVM ，因为我们不能确保数据集一定无噪音；
• 这里推荐两个台大老师 SVM 的实现：
  1. 专门解 Linear SVN ：LIBLINEAR — A Library for Large Linear Classification
  2. 专门解 Dual Kernel SVM ：LIBSVM — A Library for Support Vector Machines

回想 soft-margin SVM 中我们用 ${\xi }_n$ 作为 margin violation 的标记：

$$\begin{array}{rl}& \underset{b,\mathbf{w},\xi }{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\cdot \sum _{n=1}^N{\xi }_n\\ & \text{ s.t. }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\ge 1-{\xi }_n,\text{and }{\xi }_n\ge 0\text{ for all }n\end{array}$$

由果溯因，如果我们已经确定了 SVM 的参数 $(b,\mathbf{w})$ ，那么违反边界限制的样本点的违反程度 ${\xi }_n=1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b)$ ，而不违反边界限制的违反程度 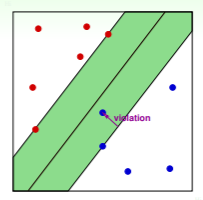${\xi }_n=0$ ，因此可以推出 ${\xi }_n=\max \{1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b),0\}$ ： 此时就可以抛去限制，得到 soft-margin SVM 的关系式为：

$$\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\cdot \sum _{n=1}^N\max \{1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b),0\}$$

这个形式与 正则化 的过程十分类似：

$$\min \frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum \widehat{\text{err}}$$

因此我们不妨将 soft-margin SVM 的关系式就看作 L2 正则化：

$$\min \frac{\lambda }{N}{\mathbf{w}}^T\mathbf{w}+\frac{1}{N}\sum \text{err}$$

不过这个关系式并不能直接套用正则化一节中的解法，因为一方面这不是 QP 问题，另一方面 $\max$ 函数可能不可微，因此我们使用 $\mathrm{Primal}\to \mathrm{Dual}\to \mathrm{Kernel}$ 的学习路线。

我们在 初识 SVM 时 就类比过正则化与 SVM 的关系，现在我们进一步考虑 soft-margin 与 L2 正则化的关系：

• 
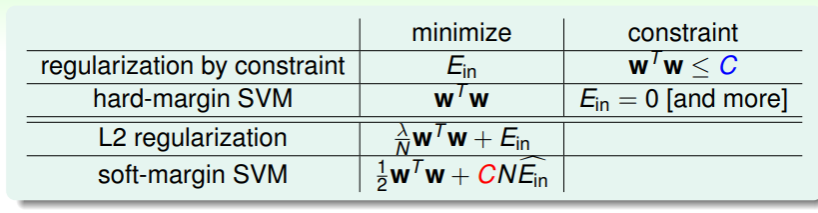
• 可以得知，越大的边界限制，对应了越小的 hyperplane 数量，也对应了 L2 正则化中越短的 $\mathbf{w}$ ；
• 而 soft-margin 这个特点其实就对应了正则化中特定的 $\widehat{\text{err}}$ ，意即容忍一定量的犯错；
• 而不论是正则化中的限制 $C$ ，还是 soft-margin SVM 的关系式中最小化目标的系数 $C$ ，其值越大，就对应越小的 $\lambda$ ，即越小的正则化；

练习：理解 soft-margin SVM 中参数 $C$ 的意义

SVM versus Logistic Regression

回想我们在 二元分类问题中的错误评估 ，都是基于线性模型计算得到的分数 $s={\mathbf{w}}^T{\mathbf{z}}_n+b$ 进行处理：

• 以 PLA 为代表的错误评估为 ${\text{err}}_{0/1}(s,y)=[ys\le 0]$ ，
• 而 SVM 的错误评估为 ${\widehat{\text{err}}}_{SVM}(s,y)=\max \{1-ys,0\}$ ，
• 将这两个错误评估函数绘图，则得到：
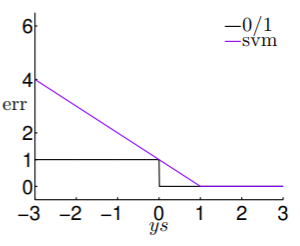
• 这表明 SVM 的错误评估是 PLA 的错误评估的上界，且是凸函数，形象地称 ${\widehat{\text{err}}}_{SVM}$ 为 hinge error measure ；
• 另外再考虑 Logistic Regression 的错误评估 ${\text{err}}_{SCE}(s,y)={\log }_2(1+e^{-ys})$ ，它也是 ${\text{err}}_{0/1}$ 的上界，绘图得：
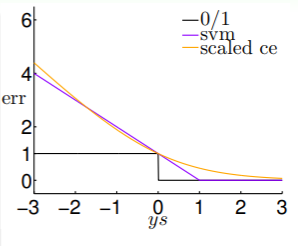
• 上图告诉我们，在 $ys$ 的定义域中，SVM 和 Logistic Regression 两种模型的错误评估有如下关系：
• 因此不妨视 $\mathrm{SVM}\approx \text{ L2-regularized logistic regression}$ ；

再一次综合回顾 PLA、soft-margin SVM、regularized logistic regression 三种模型：

• 
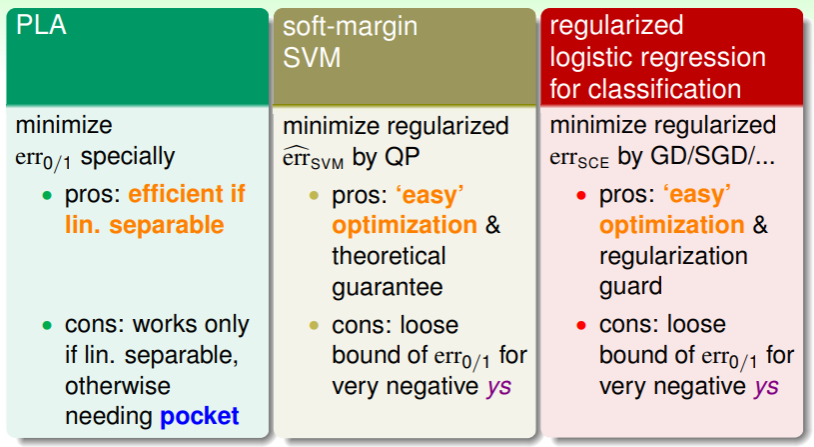
• PLA 的错误评估函数是特定的，其优势是在线性可分数据集上高效，但败也萧何，若是数据集不是线性可分，就要使用 pocket 策略改进；
• soft-margin SVM 的错误评估函数是 QP 问题，其优势是可以轻松地找到最优解，并且有丰富的理论保障，但是它在 $ys$ 非常小（预测错误得离谱）时，仅仅是 ${\text{err}}_{0/1}$ 的宽松上界；
• regularized LogReg 的错误评估函数在求最小值时，使用的是随机梯度下降或梯度下降法，不过优势劣势与 soft-margin SVM 几乎完全相同；

练习：何时 SVM 和 PLA 的错误评估结果相同？

SVM for Soft Binary Classification

讨论完 SVM 在二元分类中的错误评估，我们自然就要运用它实现二元分类，并且前文提到 soft-margin SVM 与 regularized logistic regression 非常类似，因此我们是否可以运用这一点实现二元分类呢？

• 
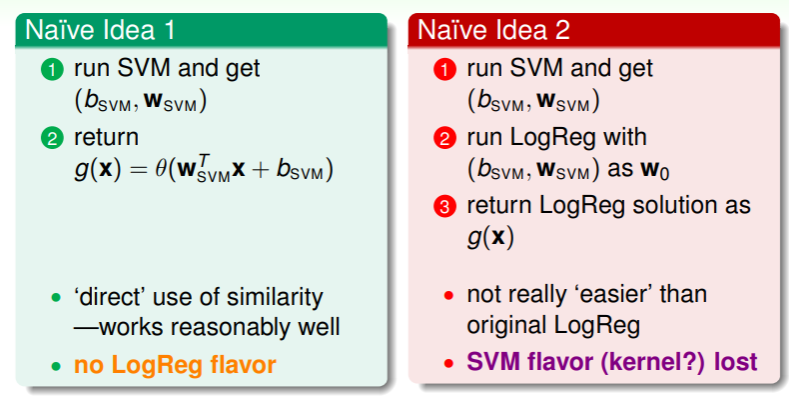
• 直觉地想法是，要么运用 SVM 得到 $(b,{\mathbf{w}}_{SVM})$ 参数，直接代入 logistic regression 中作为判断结果；要么将 SVM 运行得到的 $(b,{\mathbf{w}}_{SVM})$ 作为 ${\mathbf{w}}_0$ ，然后从此开始运行 logistic regression 算法；
• 不过这两种直觉的想法都只利用了 SVM 或 logistic regression 的一方的特点，若要综合利用，还要再次考量。

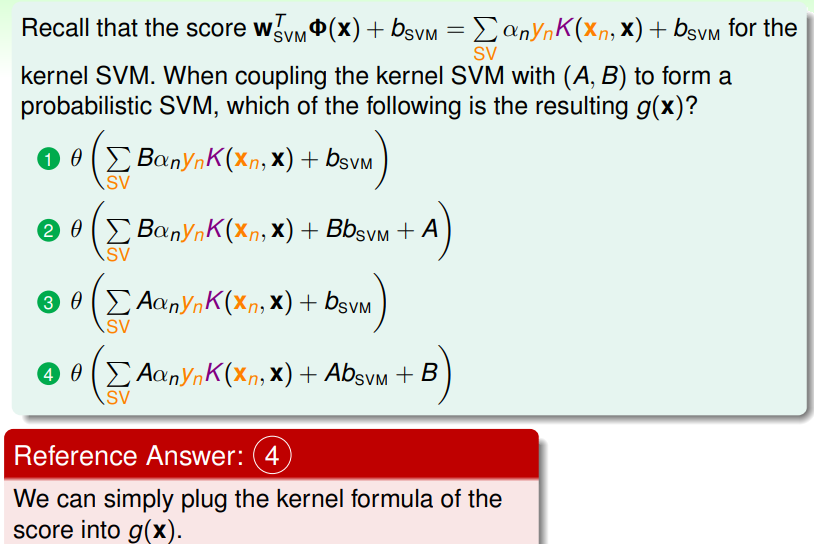
若要综合 SVM 和 logistic regression 两种模型的特点，我们应当如下设置最佳估计：

$$g(\mathbf{x})=\theta \left(A\cdot ({\mathbf{w}}_{SVM}^T\Phi (\mathbf{x})+b_{SVM})+B\right)$$

此处核心是 SVM 风格的参数，${\mathbf{w}}_{SVM}$ 和 $b_{SVM}$ ；然后通过 logistic regression 风格的参数 $A$ 进行放缩和参数 $B$ 进行偏移后，得到最大的可能、作为最后的得分：

• 通常 SVM 运算得出的 ${\mathbf{w}}_{SVM}$ 比较好时，$A>0$ ，
• 而 $b_{SVM}$ 比较好时，$B\approx 0$ ；

如此，得到的 LogReg Problem 为：

$$\underset{A,B}{\min }\frac{1}{N}\sum _{n=1}^N\log \left(1+\exp \left(-y_n(A\cdot (\underset{{\Phi }_{SVM}({\mathbf{x}}_n)}{\underbrace{{\mathbf{w}}_{SVM}^T\Phi (\mathbf{x})+b_{SVM}}})+B)\right)\right)$$

这种结合式的模型实际上就是在经过 SVM 转化的数据集上进行 LogReg 。

这个模型最初由 Platt 提出：

• 

练习：理解组合式模型

Kernel Logistic Regression

Kernel Function 的本质是向量之内积，因此权重向量与特征向量的内积可以写成如下形式：

$${\mathbf{w}}_{\ast }^T\mathbf{z}=\sum _{n=1}^N{\beta }_n{\mathbf{z}}_n^T\mathbf{z}=\sum _{n=1}^N{\beta }_{n}K({\mathbf{x}}_n,\mathbf{x})$$

这里意味着能够求得最佳权重向量 ${\mathbf{w}}_{\ast }$ 的条件就是——权重向量是样本特征向量的线性组合。如 SVM、PLA、LogReg 三种模型：

• 

那么何时存在 ${\mathbf{z}}_n$ 表达能够表达最佳权重向量 ${\mathbf{w}}_{\ast }$ 的条件？实际上，对任何形如：

$$\underset{\mathbf{w}}{\min }\frac{\lambda }{N}{\mathbf{w}}^T\mathbf{w}+\frac{1}{N}\sum _{n=1}^N\text{err}(y_n,{\mathbf{w}}^T{\mathbf{z}}_n)$$

的 L2 正则化的线性模型，都有最佳权重向量 ${\mathbf{w}}_{\ast }$ 是所有样本的特征向量的线性组合：${\mathbf{w}}_{\ast }=\sum _{n=1}^N{\beta }_n{\mathbf{z}}_n$ ，这个定理称为 Representer Theorem 。要证明它也比较直观：

• 
• 将最佳权重向量 ${\mathbf{w}}_{\ast }$ 分解为两个向量之和——一个是由样本集中向量可以线性表示出来的向量 ${\mathbf{w}}_{||}$ ，即有 ${\mathbf{w}}_{||}\in \text{span}({\mathbf{z}}_n)$ ；另一个是垂直于样本 ${\mathbf{z}}_n$ 可以展开的空间的向量 ${\mathbf{w}}_{\perp }$ ，即有 ${\mathbf{w}}_{\perp }\perp \text{span}({\mathbf{z}}_n)$ ；
• 因此如果最终最佳权重向量 ${\mathbf{w}}_{\ast }$ 可以由样本集中线性表示，那就意味着 ${\mathbf{w}}_{\perp }=0$ ；
• 但如果真的存在 ${\mathbf{w}}_{\perp }\ne 0$ ，那么考虑错误评估 $\text{err}(y_n,{\mathbf{w}}_{\ast }^T{\mathbf{z}}_n)=\text{err}(y_n,({\mathbf{w}}_{||}+{\mathbf{w}}_{\perp }{)}^T{\mathbf{z}}_n)$ ，由于 ${\mathbf{w}}_{\perp }$ 是垂直的，因此其内积必然为 0 ，这个等式成立，然而 ${\mathbf{w}}_{\ast }$ 的长度与 ${\mathbf{w}}_{||}$ 却并不相同：${\mathbf{w}}_{\ast }^T{\mathbf{w}}_{\ast }={\mathbf{w}}_{||}^T{\mathbf{w}}_{||}+2{\mathbf{w}}_{||}^T{\mathbf{w}}_{\perp }+{\mathbf{w}}_{\perp }^T{\mathbf{w}}_{\perp }>{\mathbf{w}}_{||}^T{\mathbf{w}}_{||}$ ，这说明存在另一个线性组合 ${\mathbf{w}}_{||}$ 比最优权重向量 ${\mathbf{w}}_{\ast }$ 还要更优，这便发生了矛盾。

综上，我们可以得知，任意 L2 正则化的线性模型都是可以运用 kernel trick 的（ML 中称为可以被 kernelized）。

span(vector)的含义是什么？

在线性代数中，“span(z)” 表示由向量 z 的所有线性组合组成的集合。具体来说，如果有一个向量 z，那么 span(z) 包含所有可以通过对 z 进行线性组合（使用标量乘法和向量加法）而得到的向量。这意味着 span(z) 包含所有形如 c * z 的向量，其中 c 是任意标量。

换句话说，span(z) 是 z 所在的向量空间，它是由 z 张成的子空间。这个子空间包含所有可以通过在 z 上乘以不同的标量来得到的向量，形成一个由 z 所生成的线性子空间。

在几何上，span(z) 表示 z 所在的向量空间中的所有可能方向。如果 z 是一个二维向量，那么 span(z) 将是平面上通过原点的所有可能向量的集合。如果 z 是三维向量，那么 span(z) 将是通过原点的整个三维空间的所有可能向量的集合。

因此，转而求解 L2 正则化的 LogReg 问题：

$$\underset{\mathbf{w}}{\min }\frac{\lambda }{N}{\mathbf{w}}^T\mathbf{w}+\frac{1}{N}\sum _{n=1}^N\log \left(1+e^{-y_n{\mathbf{w}}^T{\mathbf{z}}_n}\right)$$

我们必然会得到由样本集线性组合而成的最优权重向量 ${\mathbf{w}}_{\ast }$ ，故而运用 kernel function 代替其中的向量内积，我们可以求解最优的参数 $\beta$ ：

$$\underset{\mathbf{\beta }}{\min }\frac{\lambda }{N}\sum _{n=1}^N\sum _{m=1}^N{\beta }_n{\beta }_{m}K({\mathbf{x}}_n,{\mathbf{x}}_m)+\frac{1}{N}\sum _{n=1}^N\log \left(1+e^{-y_n\sum _{m=1}^N{\beta }_{m}K({\mathbf{x}}_m,{\mathbf{x}}_n)}\right)$$

这是一个无限制的最优化问题，求解方法就是梯度下降或随机梯度下降，这个模型称为 kernel logistic regression —— 即，在 L2 正则化 LogReg 问题中使用 kernel 技巧的 representer 定理。

更进一步地深挖 KLR 模型：

• 其中 $\sum _{m=1}^N{\beta }_{m}K({\mathbf{x}}_m,{\mathbf{x}}_n)$ 的含义是：变量 $\mathbf{\beta }$ 和转换后数据样本 $(K({\mathbf{x}}_1,{\mathbf{x}}_n),K({\mathbf{x}}_2,{\mathbf{x}}_n),...,K({\mathbf{x}}_N,{\mathbf{x}}_n),)$ 的内积；
• $\sum _{n=1}^N\sum _{m=1}^N{\beta }_n{\beta }_{m}K({\mathbf{x}}_n,{\mathbf{x}}_m)$ 的含义是一个特殊的正则化器 ${\mathbf{\beta }}^T\mathrm{K}\mathbf{\beta }$ ；
• KLR 可以看作是运用 kernel function 在样本转换和 kernel 正则化的线性模型，也可以看作是 kernel 转换和 L2 正则化的线性模型
• 另外要注意，与 SVM 中系数 ${\alpha }_n$ 可以为 0 不同，KLR 中系数 ${\beta }_n$ 通常不为 0 ；

练习：理解组合模型的实际维数