24-Bitmap

ADT

$\forall 0\le k\le U:$

• $k\in S?$ bool test (int k);
• $S\cup \{k\}$ void set (int k);
• $S\backslash \{k\}$ void clear (int k);

class Bitmap {
private:
	unsigned char * M;
	Rank N, _sz;
public:
	Bitmap( Rank n = 8 )
		{ M = new unsigned char[ N = (n+7)/8 ]; memset( M, 0, N ); _sz = 0; }
	~Bitmap() { delete [] M; M = NULL; _sz = 0; }
	void set( int k ); 
	void clear( int k ); 
	bool test( int k );
};

实现

bool test ( int k ) { expand( k ); return M[ k >> 3 ] & ( 0x80 >> (k & 0x07) ); }
void set ( int k ) { expand( k ); _sz++; M[ k >> 3 ] |= ( 0x80 >> (k & 0x07) ); }
void clear( int k ) { expand( k ); _sz--; M[ k >> 3 ] &= ~( 0x80 >> (k & 0x07) ); }

应用

大数据、高重复

老问题：int A[n] 的元素均取自 [0, m) 如何剔除其中的重复者？

之前的办法是：先排序、再扫描—— $O(n\log n+n)$

但对于数据量大、重复度极高的情况，比如，10,000,000,000个24位无符号整数：

• 重复的数据很多：2^24 = m << n = 10
• 如果采用内部排序算法，至少需要 4 * n = 40GB 内存，即便能够申请到这么多空间，频繁的 I/O 将导致整体效率的低下——利用好 m<<n 的条件。

Bitmap B( m ); //O(m)
for (Rank i = 0; i < n; i++)
	B.set( A[i] ); //O(n)
for (Rank k = 0; k < m; k++)
	if ( B.test( k ) )
		/* ... */; //O(m)

总体运行时间 = O(n + m) = O(n) 空间 = O(m)

• 就上例而言，降至： m/8 = 2^21 = 2MB << 40GB
• 即便 m = 2^32，也不过： 2^29 = 0.5GB

筛法求素数

void Eratosthenes( Rank n, char * file ) {
	Bitmap B( n ); 
	B.set( 0 );
	B.set( 1 );
	for ( Rank i = 2; i < n; i++ )
		if ( ! B.test( i ) )
			for ( Rank j = 2*i; j < n; j += i )
				B.set( j );
	B.dump( file );
}

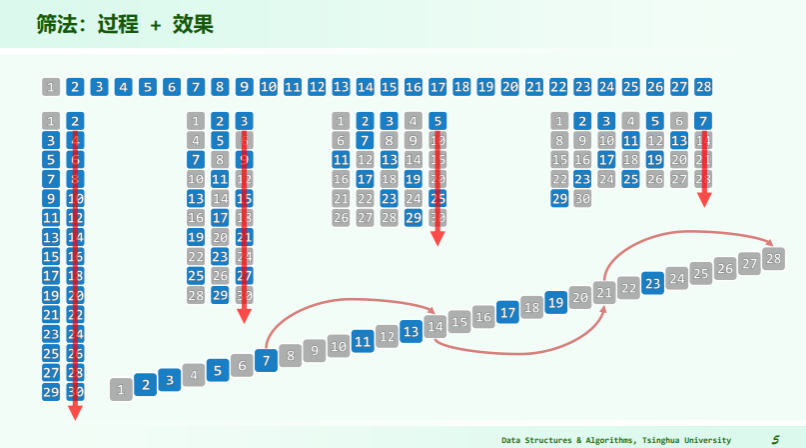
不计内循环，外循环自身每次仅一次加法、两次判断，累计 O (n) 内循环每趟迭代 O (n/i) 步，由素数定理外循环至多 n/lnn 趟，累计耗时

$$\begin{array}{rl}& \frac{n}{2}+\frac{n}{3}+\frac{n}{5}+...\\ & <\frac{n}{2}+\frac{n}{3}+\frac{n}{4}+...+\frac{n}{\frac{n}{\ln n}}\\ & =O(n(\ln (\frac{n}{\ln }n)-1))\\ & =O(n\ln n-n\ln (\ln (n)))\\ & =O(n\log n)\end{array}$$

内循环的起点“2 * i”可改作“i * i”；外循环的终止条件“i < n”可改作“i * i < n” //为什么？

内循环每趟迭代 O (max (1, n/i-i)) 步，外循环至多 √n/ln√n 趟，耗时减少 //从渐近角度看呢？

快速初始化

Bitmap 的构造函数中，通过 memset(M,0,N) 统一清零 这一步只需 O(1) 时间？不，实际上仍等效于诸位清零，O(n) ！

• 尽管这并不会影响上例的渐近复杂度，但并非所有问题都是如此
• 有时，对于大规模的散列表（第 09 章），初始化的效率直接影响到实际性能
  • 例如： 第13章中 bc[]表 的构造算法，需要 $O(|\Sigma |+m)=O(s+m)$ 时间，若能省去 bc[] 表各项的初始化，则可严格地保证是 O(m)
• 有时，甚至会影响到算法的整体渐近复杂度
  • 例如，为从 n = 10^8 个 32 位整数中找出重复者，可仿造剔除算法，因此，若能省去 Bitmap 的初始化，则只需 O(n) 时间

校验环

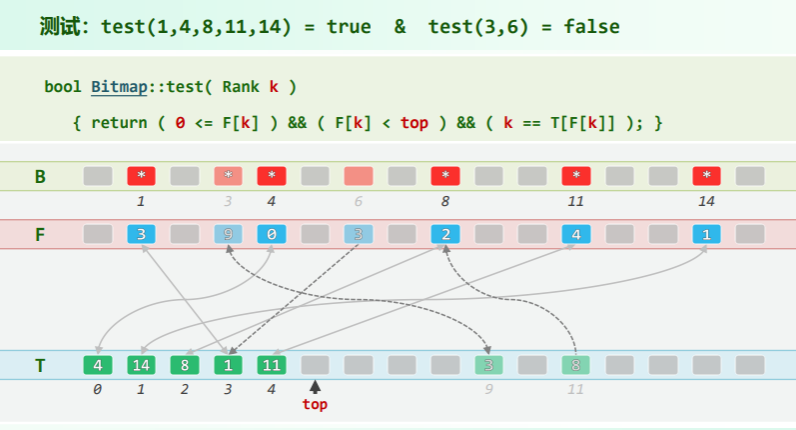
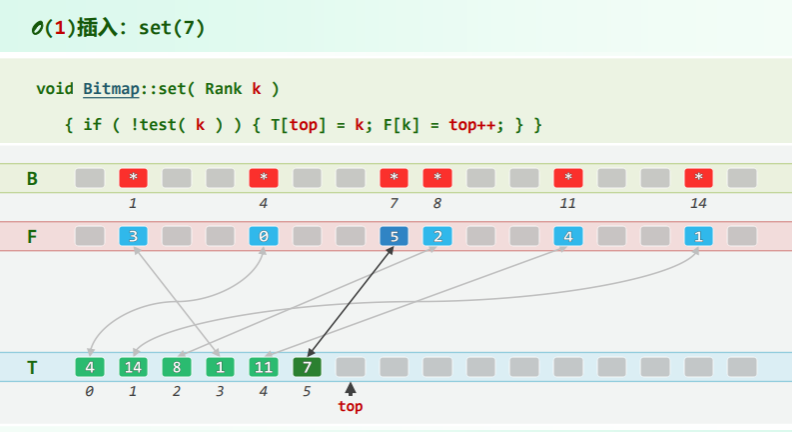
将 B[] 拆分成一对等长向量，有效位均满足： T[F[k]] == k & F[T[i]] == i

• From: Rank F[m],
• To and stack top: T[m], top = 0;

测试

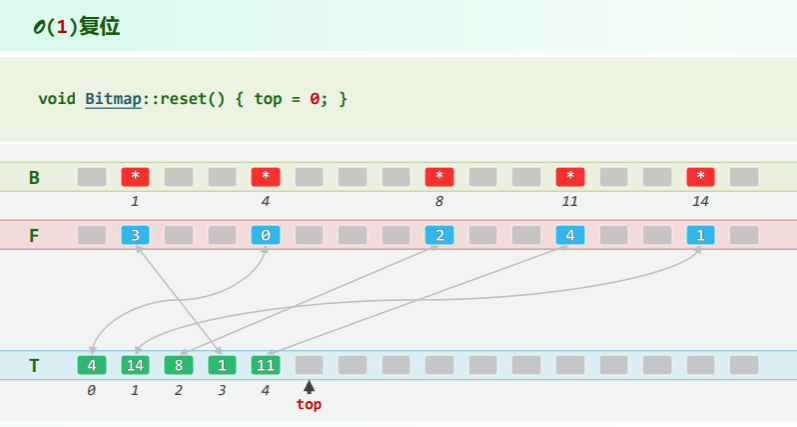
O (1) reset

O (1) set

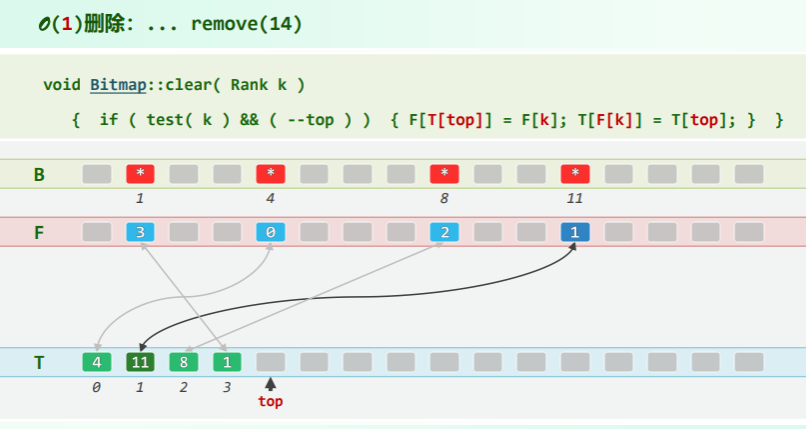
O (1) remove