70-Hash

Dictionary ADT

template <typename K, typename V> //key、value
struct Dictionary {
	virtual Rank size() = 0;
	virtual bool put( K, V ) = 0;
	virtual V* get( K ) = 0;
	virtual bool remove( K ) = 0;
};

词典中的词条只需支持判等/比对操作。

词条 entry=(key, value)，词条的集合作为 Map/Dictionary，并且关键码 key 有雷同性限制。

关键码 key 可以是任何类型，因此未必支持大小比较。

散列

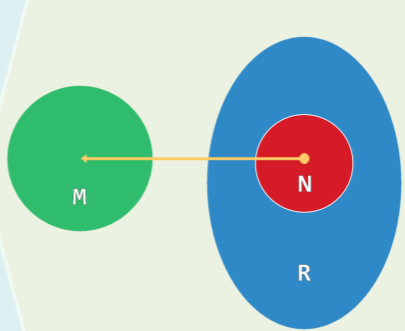
数组存放数据的查询效率很高，可以达到 O(1)。但是所有空间常常不能占满，例如以电话号码为例：

可能的电话号种数=R=10
实际可用的电话号种数=N=25000
因此实际的空间复杂度= O (R+N)，效率=25K/10^5M=0.000025%

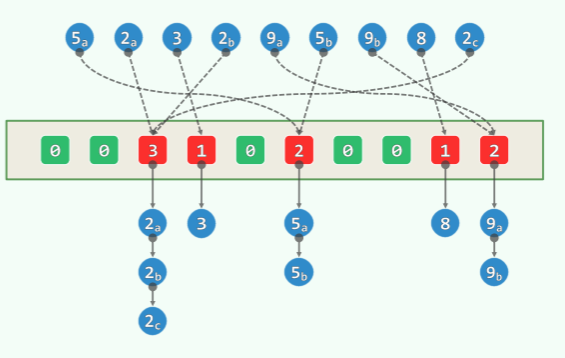
为了提高空间利用率，又保证查找速度，可以使用散列法：

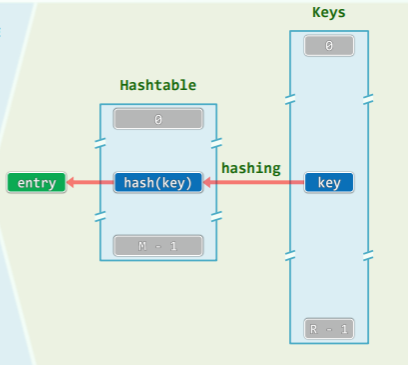
桶 bucket：直接存放或间接指向的一个词条；
Bucket array ~ Hashtable：容量 M (N<M<<R)，使得空间复杂度 O (N+M)=O (2N+C)=O (N)
定址：根据词条的 key，直接（实际是通过散列函数和冲突解决策略）确定散列表的入口
散列函数：hash (): key ⇒ &entry
“直接”：expected-O (1) ，而不是 O (1)

冲突

指不同的 key，在经过 hash 函数运算后得到相同的结果：

考虑装填因子 load factor: λ=N/M

λ越大，空间利用率越高，但相应的发生冲突的概率越高。
通过降低 λ，即增加 Hashtable 的容量 M，可以改善冲突程度，但只要 M<<R 这一条件存在，冲突就不可能杜绝。

完美散列

数据集已知且固定时，可实现完美散列（perfect hashing）

采用两级散列模式
仅需 O(n)空间
关键码之间互不冲突
最坏情况下的查找时间也不过 O (1)
不过在一般情况下，完美散列可期不可求…

生日悖论

将在座同学（对应的词条）按生日（月/日）做散列存储，散列表长 M = 365，装填因子 = 在场人数 N / 365

冲突（至少有两位同学生日相同）的可能性 P365(n) = ？ P365(1) = 0, P365(2) = 1/365, …, P365(22) = 47.6%, P365(23) = 50.7%, …

100人的集会：1 - P365(100) = 0.000,031%

因此，在装填因子确定之后，散列策略的选取将至关重要，同时，发生冲突时尽快、高效地排解也非常重要。

散列函数

评价标准

确定 determinism：统一关键码总是映射到同一地址
快速 efficiency：映射的计算时间开销为 expected-O (1)
满射 surjection：尽可能充分地利用整个散列空间 Hashtable
均匀 uniformity：关键码散射到散列表各位置的概率尽量接近，有效避免聚集 clustering 现象
- 装填因子很大时，也难以避免聚集现象的发生

除余法

hash(key) = key % M

素数的作用

据说：M 为素数时，数据对散列表的覆盖最充分，分布最均匀若取 M=2^k，效果相当于截取 key 的最后 k 位，前面的 n-k 位对地址都没有影响：

M-1 = 0000… 0|11… 11
key % M = key & (M-1)
推论：发生冲突时，当且仅当最后 k 位相同，此时发生冲突的概率极大
因而，取 M != 2^k，缺陷会有所改善
从而，M 为素数时，数据对散列表的覆盖最充分、分布最均匀

蝉的哲学：经长期自然选择，生命周期“取”作素数

蝉通常是十三龄蝉、十七龄蝉这样的素数年龄；
这里十三龄、十七龄就是除余法中的 M，而 step 是天敌的生命周期；

M 不是素数可以吗？

其实：对于理想随机的序列，表长是否素数，无关紧要！

序列的 Kolmogorov 复杂度：生成该序列的算法，最短可用多少行代码实现？

算术级数： 7 12 17 22 27 32 37 42 47 … //单调性/线性：从 7 开始，步长为5
循环级数： 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 … //周期性：12345
英文：data structures and algorithms … //局部性：频率、关联、词根、…

实际应用中的数据序列远非理想随机，上述规律性普遍存在。

缺陷

不动点：无论 M 取值如何，总有 hash (0) = 0

违背任何元素映射到任意点的概率相同的原则

相关性：[0, R)的关键码尽管平均分配至 M 个桶，但相邻关键码的散列地址也必然相邻:

MAD 法

multiply-add-divide: 取 M 为素数，a>1, b>0, a%M != 0 hash (key) = (a * key + b) % M

这里 a 是步长，消除零阶均匀的问题
b 是消除不动点的问题

数字分析法

selecting digits：抽取 key 中的某几位，构成地址

比如，取十进制表示的奇数位：hash (3141592654)=34525
不过，由于偶数位对 hash 的结果没有贡献，因此影响了函数的均匀性；

平方取中法

取 key^2的中间若干位，构成地址:

hash (123)=middle (123 * 123)=middle (1 512 9) = 512
hash (1234567)=middle (1524155677489)=556

中间位置的密度最大，由各个位置的数都参与贡献得到。

折叠法

folding：将 key 分割成等宽的若干段，取其总和作为地址

hash (123456789)=123+456+789=1368
hash (123456789)=123+654+789=1566

位异或法

XOR：将 key 分割成等宽的二进制段，经异或运算得到地址

hash (110011011)=110^011^011=110
hash (110011011)=110^110^011=011

伪随机数法

伪随机数发生器：rand (x+1)=[a * rand (x)]%M,
- M is prime && a%M !=0
- 伪随机数发生器因平台、历史版本而有差异，故程序的可移植性差；
伪随机数法：hash (key)=rand (key)=[rand (0) * a^key]%M
种子 rand (0)

// The C Programming Language 第二版p46页的伪随机数发生器

unsigned long int next = 1; //sizeof(long int) = 8
void srand(unsigned int seed) { next = seed; } //sizeof(int) = 4 or 8

int rand(void) {//1103515245 = 3^5 * 5 * 7 * 129749
	next = next * 1103515245 + 12345;
	return (unsigned int)(next/65536) % 32768;
}

// 其它伪随机数生成方法

// 利用内存分配的随机性
int rand() {
	int uninitialized;
	return uninitialized;
}

char* rand( t_size n ) {
	return ( char* ) malloc( n );
}

// 就地随地置乱(Fisher方法)
void shuffle( int A[], int n ) {
	for ( ; 1 < n; --n ) //自后向前，依次将各元素
	swap( A[ rand() % n ], A[ n - 1 ] ); //与随机选取的某一前驱（含自身）交换
} //20! < 2^64 < 21!

Fisher shuffle

Fisher 方法可以等概率生成所有 n! 种排列吗？——当然，18-Fisher-Yates-shuffle

Hashcode 与多项式法

static Rank hashCode( char s[] ) {
	Rank n = strlen(s); Rank h = 0;
	for ( Rank i = 0; i < n; i++ ) {
		h = (h << 5) | (h >> 27);
		h += s[i];
	} //乘以32，加上扰动，累计贡献
	return h;
}

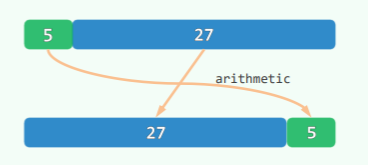
ha s h C o d e (x_{n - 1} x_{n - 2} ... x_{2} x_{1} x_{0}) = x_{n - 1} \cdot a^{n - 1} + ... + x_{2} \cdot a^{2} + x_{1} \cdot a^{1} + x_{0} = (... ((x_{n - 1} \cdot a + x_{n - 2}) \cdot a) + ... + x_{1) \cdot} a + x_{0}

还可以将字符映射为数字，再简单相加： $ha s h (s t r in g) = c ha r \in S \sum co d e (u pp er (c ha r))$

这样字符串中的相对次序的信息丢失，会引发大量冲突
甚至不同数量的字符也有可能获得同样的结果：
- He is Harry Potter 196
- I am Lord Voldemort 196
- Tom Marvolo Riddle 196

排解冲突

开放散列

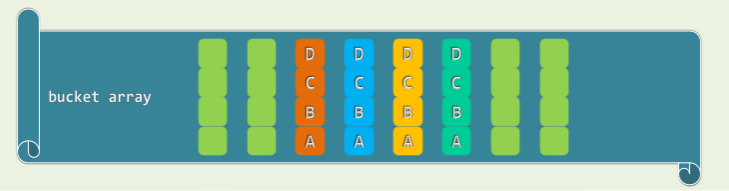
多槽位

将桶单元细分成若干槽位，以存放同一单元冲突的词条
但是问题在于，槽位究竟要分配多少？这难以确定

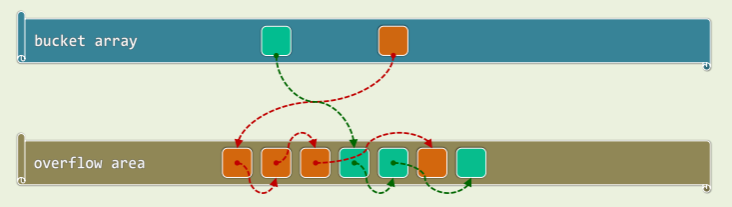
公共溢出区

单独开辟一块连续空间，发生冲突的词条，按顺序存入此区域；
结构简单，算法易于实现，
但是不冲突则以，一旦冲突，最坏情况下处理冲突词条所需的时间将正比于溢出区的规模：

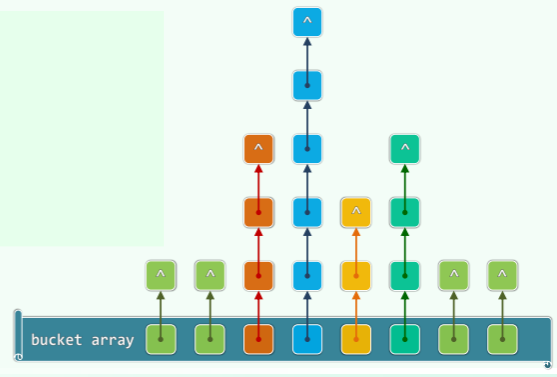
独立链

每个桶对应一个链表，存放发生冲突的一组同义词
优点：无需为每个桶预备多个槽位，任意多次冲突都可以解决，删除操作实现简单、统一
缺点：指针本身占用空间，节点的动态分配和回收需要消耗时间，更重要的是空间不连续分布，系统缓存很难生效

封闭散列

开放定址

Closed Hashing，必然要有对应的 Open Addressing

只要有必要，任何散列桶都可以接纳任何词条

Probe Sequence/Chain

为每个词条，都需事先约定若干备用桶，优先级逐次下降
查找算法：沿试探链，逐个转向下一桶单元，直到
- 命中成功，或者
- 抵达一个空桶（存在则必能找到？）而失败

相应地，试探链又应如何约定？

线性试探

Linear Probing：

一旦冲突，则试探后一紧邻的桶，直到命中或抵达空桶
在散列表内部解决冲突，无需附加的指针、链表或溢出区等，整体结构保持简洁。只要还有空桶，迟早会找到
新增非同义词之间的冲突——数据堆积（clustering）现象严重
好在，试探链连续，数据局部性良好
通过装填因子，冲突与堆积都可有效控制
插入：新词条若尚不存在，则存入试探终止处的空桶
试探链可能因而彼此串接、重叠！
删除：不能直接清除命中的桶——经过它的试探链都将因此断裂，导致后续词条丢失——明明存在，却访问不到
- 懒删除：仅做标记，不对试探链做更多调整——此后，带标记的桶，角色因具体的操作而异
- 查找词条时，被视作“必不匹配的非空桶”，试探链在此得以延续
- 插入词条时，被视作“必然匹配的空闲桶”，可以用来存放新词条

/**
 * 沿关键码k的试探链(线性试探)，找到与之匹配的桶；
 **/
template <typename K, typename V>
Rank Hashtable<K, V>::probe4Hit( const K& k ) {
	for ( Rank r = hashCode( k ) % M;; r = ( r + 1 ) % M ) //按除余法确定起点，线性试探
	    if ( !ht[r] && !removed->test( r ) || ht[r] && ( k == ht[r]->key ) ) //跳过懒惰删除的桶
	        return r; //只要N+L < M，迟早能终止
}

/**
 * 沿关键码k的试探链，找到首个可用空桶；
 **/
template <typename K, typename V>
Rank Hashtable<K, V>::probe4Free( const K& k ) {
	for ( Rank r = hashCode( k ) % M;; r = ( r + 1 ) % M ) //按除余法确定起点，线性试探
	    if ( !ht[r] ) //只要有空桶（无论是否带有懒惰删除标志）
	        return r; //迟早能找到
}

重散列

// rehash
/**
 * 重散列：空桶太少时对散列表重新整理：
 * 扩容，再将词条逐一移入新表
 * 散列函数的定址与表长M直接相关，故不可简单地批量复制原桶数组
 **/
template <typename K, typename V>
void Hashtable<K, V>::rehash() {
	Rank oldM = M; Entry<K, V>** oldHt = ht;
	M = primeNLT( 4 * N, 1048576, PRIME_TABLE ); //容量至少加倍（若懒惰删除很多，可能反而缩容）
	ht = new Entry<K, V>*[M]; N = 0; memset( ht, 0, sizeof( Entry<K, V>* ) * M ); //初始化桶数组
	release( removed ); removed = new Bitmap( M ); //懒惰删除标记
   
	for ( Rank i = 0; i < oldM; i++ ) //扫描原表
	    if ( oldHt[i] ) //将每个非空桶中的词条
	        put( oldHt[i]->key, oldHt[i]->value ); //转入新表
	release( oldHt ); //释放――因所有词条均已转移，故只需释放桶数组本身
}

Rank primeNLT( Rank c, Rank n, char* file ) { //根据file文件中的记录，在[c, n)内取最小的素数
   Bitmap B( file, n ); // file已经按位图格式记录了n以内的所有素数，因此只要
   while ( c < n ) //从c开始，逐位地
      if ( B.test( c ) ) c++; //测试，即可
      else return c; //返回首个发现的素数
   return c; //若没有这样的素数，返回n（实用中不能如此简化处理）
}

template <typename K, typename V> struct Entry { //词条模板类
   K key; V value; //关键码、数值
   Entry( K k = K(), V v = V() ) : key( k ), value( v ){}; //默认构造函数
   Entry( Entry<K, V> const& e ) : key( e.key ), value( e.value ){}; //基于克隆的构造函数
   bool operator<( Entry<K, V> const& e ) { return key < e.key; } //比较器：小于
   bool operator>( Entry<K, V> const& e ) { return key > e.key; } //比较器：大于
   bool operator==( Entry<K, V> const& e ) { return key == e.key; } //判等器：等于
   bool operator!=( Entry<K, V> const& e ) { return key != e.key; } //判等器：不等于
}; //得益于比较器和判等器，从此往后，不必严格区分词条及其对应的关键码

插入：

template <typename K, typename V>
bool Hashtable<K, V>::put( K k, V v ) { //散列表词条插入
	if ( ht[ probe4Hit( k ) ] ) return false; //雷同元素不必重复插入
	Rank r = probe4Free( k ); //为新词条找个空桶（只要装填因子控制得当，必然成功）
	ht[ r ] = new Entry<K, V>( k, v ); ++N; //插入
	if ( removed->test( r ) ) removed->clear( r );  //懒惰删除标记
	if ( (N + removed->size())*2 > M ) rehash(); //若装填因子高于50%，重散列
	return true;
}

删除：

template <typename K, typename V> bool Hashtable<K, V>::remove( K k ) { //散列表词条删除算法
	int r = probe4Hit( k ); if ( !ht[r] ) return false; //确认目标词条确实存在
	release( ht[r] ); ht[r] = NULL; --N; //清除目标词条
	removed->set(r); //更新标记、计数器
	if ( removed->size() > 3*N ) rehash(); //若懒惰删除标记过多，重散列
	return true;
}

平方试探

Quadratic Probing:

以平方数为距离，确定下一试探桶的位置：
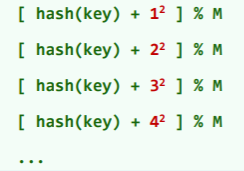
能够缓解数据聚集现象，试探链上各桶之间的距离线性递增，一旦冲突能很快离开冲突局部；
但是未必能找到所有空桶：表长为素数时，对于装填因子λ<0.5 就一定能找出，否则不行：
- 考虑{0,1,2,3,4,…,}^2 % 12 = {0,1,4,9},
- {0,1,2,3,4,…,}^2 % 11 = {0,1,4,9,5,3}
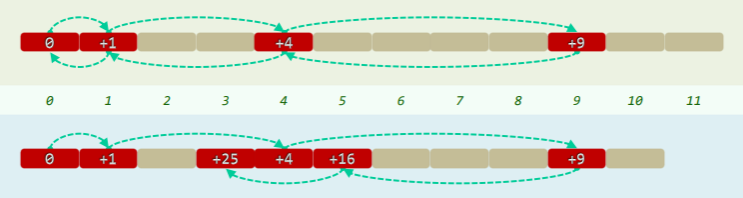
- M 为合数，则 n^2 % M 的取值小于 $⌈ \frac{M}{2} ⌉$ 种
- M 为素数，则 n^2 % M 恰有 $⌈ \frac{M}{2} ⌉$ 种取值，且由试探链的前 $⌈ \frac{M}{2} ⌉$ 项取遍；

因此，试探链的前缀必须足够长，且无重复：反证：

假设存在 $0 \leq a < b < ⌈ \frac{M}{2} ⌉$ ，使得沿着试探链，第 a 项和第 b 项彼此冲突
于是：a^2 和 b^2 自然关于 M 同余，亦即 $a^{2} \equiv b^{2} (m o d M), b^{2} - a^{2} = (b + a) (b - a) \equiv 0 (m o d M)$
然而， $0 < b - a \leq b + a < ⌈ \frac{M}{2} ⌉ + (⌈ \frac{M}{2} ⌉ - 1) \leq ⌈ \frac{M}{2} ⌉ + ⌊ \frac{M}{2} ⌋ = M$ 无论 b-a 还是 b+a 都不可能整除 M
那么，另一半的桶，可否也利用起来呢… (再加一层线性散列)

双向平方试探

策略：交替地沿两个方向试探，均是平方的距离。

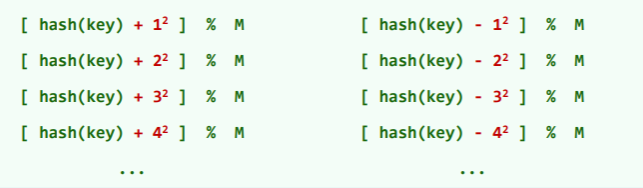
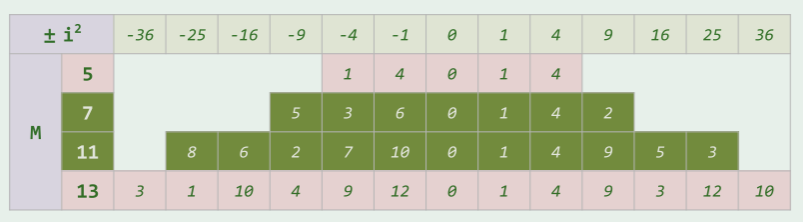
正向和反向的子试探链，各自包含 $⌈ \frac{M}{2} ⌉$ 个互异的桶：
$- ⌊ \frac{M}{2} ⌋, ..., - 3, - 2, - 1, 0, 1, 2, 3, ..., ⌊ \frac{M}{2} ⌋$
除了起点 0，且表长 M 为素数并可以表示为 M=4k+3 的形式，就可以保证试探链的前 M 项均互异
- Two-Square Theorem of Fermat: 整数 p 不能表示为一对整数的平方和，当且仅当 $p \equiv 3 (m o d 4)$
- 注意到 $(u^{2} + v^{2}) (s^{2} + t^{2}) = (u s + v t)^{2} + (u t - v s)^{2} = (u s - v t)^{2} + (u t + v s)^{2}$
- 可以推知，自然数 n 可以表示为一对整数的平方和，当且仅当 n 的每一 M=4k+3 类素因子均为偶数次方

双散列

预先约定第二个散列函数 hash2 (key, i)，在发生冲突时，由冲突确定偏移量，确定下一试探的位置： $[ha s h (k ey) + i = 1 \sum k ha s h 2 (k ey, i)] % M$

比较好用的试探可以是：

线性试探： $ha s h 2 (k ey, i) \equiv 1$
平方试探： $ha s h 2 (k ey, i) = 2 i - 1$
更一般的，偏移增量同时与 key 相关

桶排序

使用情形

对[0, m)区间内的 n 个互异整数借助散列表 H[]作排序：

若 n<m ，即是表长>整数种类数，则所需空间 O (m)，所需时间 O (n)
若允许重复，m<<n，即是表长<<整数的数量（整数可以重复），使用独立链法，则可以得到空间复杂度 O (m+n)，时间复杂度 O (n)

最大缝隙问题

描述：任意 n 个互异点，将实轴分为 n-1 个有界区间，哪一段最长？

暴力方法：

对所有点排序； //Ω(nlogn)
依次计算相邻点对的间距，保留最大者； //Θ(n)

桶策略：

找到最左点和最右点； //O (n)
将有效范围均匀地划分为 n-1 个段（共 n 个桶）//O (n)
通过散列，将各点归入对应的桶 //O (n)
在各桶中，动态记录最左、最右点 //O (n)
算出相邻（非空）桶之间的距离 //O (n)
最大距离即是 MaxGap //O (n)

图中红色区块表示区段内有点存在，亦即，在 MaxGap 问题中这个区间内只有最右者和最左者有价值，且该区段可以直接排除——不会是 MaxGap 的可选值；但反之，是 MinGapd 的可选值；
正确性：MaxGap 至少跨越两个桶——MaxGap 不能局限于某一个桶内；
对应的 MinGap 问题，如何确定 n-1 段有界区间中的最短区间：
- 同样是桶策略，只需考查单个桶中最短的区间即可

基数排序

思路

词典序：关键码由多个域组成： $k_{d}, k_{d - 1}, ..., k_{1}$ ，将各域视作字母，则关键码即是单词——字典的排序方式。

由此导出基数排序的思想——自 $k_{1}$ 到 $k_{d}$ ，低位优先的顺序依次以各域为序做一趟桶排序：

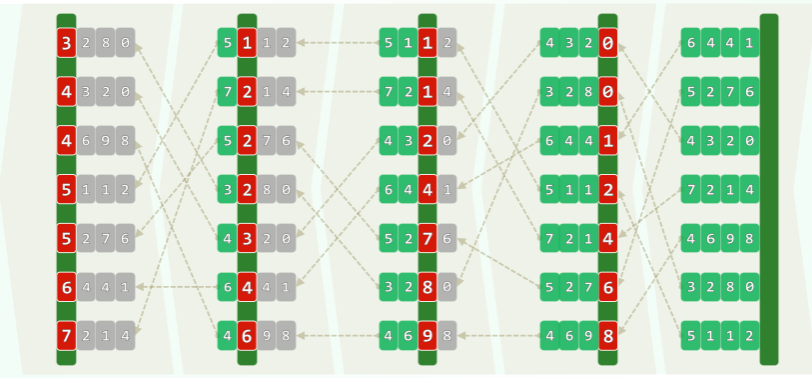
正确性：
- 归纳假设：前 i 趟排序后，所有词条关于低 i 位有序
- 假设前 i-1 趟均成立，则考查第 i 趟排序之后的情况，无非两种情况：
  - 凡第 i 位不同的词条，即便此前曾是逆序，现在必已转为有序；
  - 凡第 i 位相同的词条，得益于桶排序的稳定性，必保持原有次序（如果底层排序算法不是稳定的，那么基数排序的结果不能保证准确）；
时间成本=各趟桶排序的所需时间之和
- = $n + 2 m_{1} + n + 2 m_{2} + n + 2 m_{3} + ... + n + 2 m_{d}$ // $m_{k}$ 是各域的取值范围
- =O (d*(n+m)) //m=max{ $m_{1}, m_{2}, ..., m_{d}$ }
- 当 m=O (n)且 d 可视作常数时，可以达到 O (n)的效率！

实现

//以二进制无符号整数为例
using U = unsigned int; //约定：类型T或就是U；或可转换为U，并依此定序

template <typename T> //对列表中起始于位置p、宽度为n的区间做基数排序
void List<T>::radixSort(ListNodePosi<T> p, Rank n) { 
	// valid(p) && Rank(p) + n <= size

	ListNodePosi<T> head = p->pred; //待排序区间为(head, tail)
	ListNodePosi<T> tail = p; 
	for ( Rank i = 0; i < n; i++ ) tail = tail->succ;
	for ( U radixBit = 0x1; radixBit && (p = head); radixBit <<= 1 ) //以下反复地
	    for ( Rank i = 0; i < n; i++ ) //根据当前基数位，将所有节点
	        radixBit & U (p->succ->data) ? //分拣为后缀（1）与前缀（0）
	            insert( remove( p->succ ), tail ) : p = p->succ;
}//为避免remove、insert接口的低效率，可以拓展List::move(p,tail)接口，将节点p直接移至tail之前

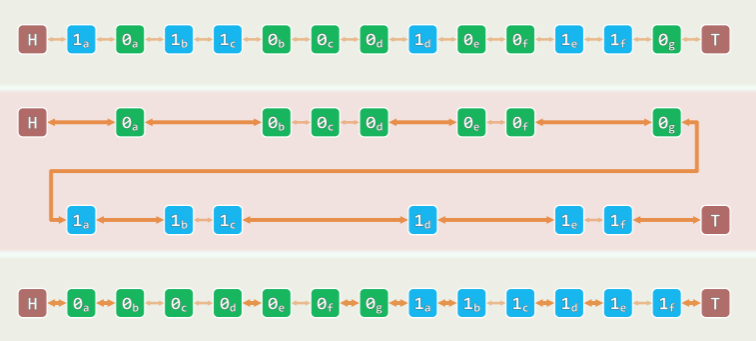
对数密度的整数集排序

设 d>1 为常数，考查取自[0, n^d)范围内的 n 个整数：

常规密度= $\frac{n}{n ^{d}} = \frac{1}{n ^{(d - 1)}} \sim 0$ ;
对数密度= $\frac{l n n}{l n n ^{d}} = \frac{1}{d} = O (1)$
即这类整数集的对数密度不超过常数；
若取 d=4，则即便是 64 位的 long 型整数，也只需 $n > (2^{64})^{\frac{1}{4}} = 2^{16} = 65536$
对于这类整数集，设计效率 o(nlogn)的排序算法。

利用基数排序设计线性排序算法：

预处理：将所有元素转换为 n 进制形式 $x = (x_{d}, ..., x_{2}, x_{1})$
于是，每个元素均转化为 d 个域，故可直接套用 Radixsort 算法
排序时间=d (n+n)=O (n)
突破此前确定的Ω(nlogn)下界的原因：整数取值范围有限制，且不再是基于比较的计算模式；
并且进制转换需要 O (n * d)时间

计数排序

思路

如何优化“小集合+大数据”的对数密度的数据集的排序？

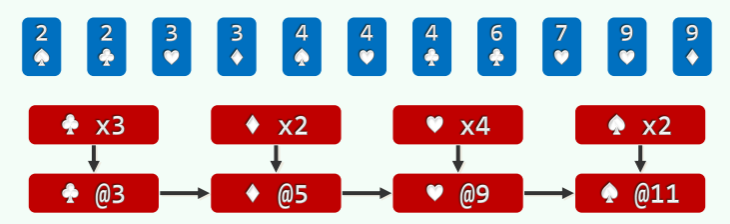
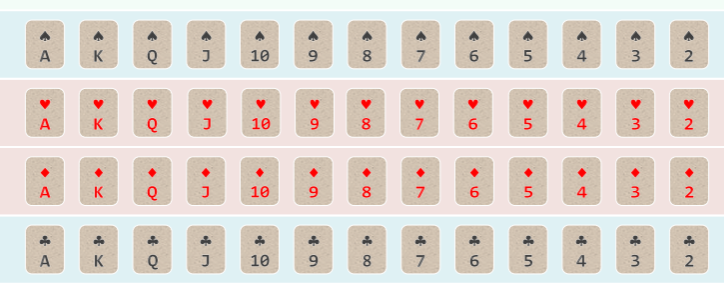以纸牌排序为例 (n>>m=4)，假设已按点数排序，接下来按花色排序：

经过分桶，统计出各种花色的数量; //O (n)
自前向后扫描个桶，依次累加，即可确定各套花色所处的秩的区间： $[0, 3) + [3, 5) + [5, 9) + [9, 11)$ //O (m)
自后向前扫描每一张牌，对应桶的计数减一，即是其所在最终有序序列中对应的秩; //O (n)

举例

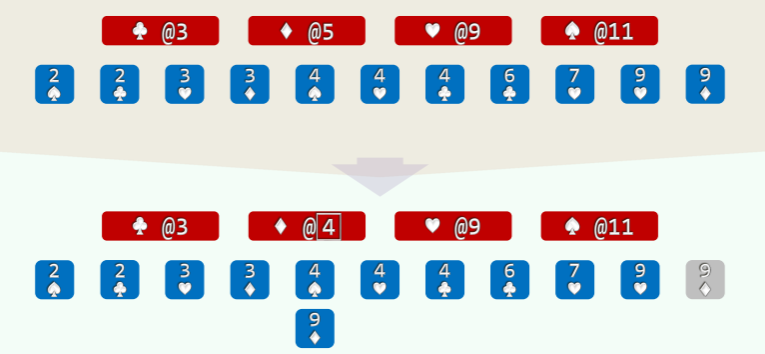
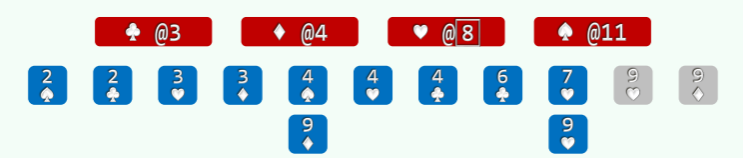
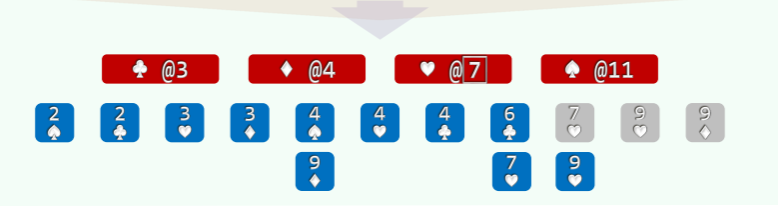
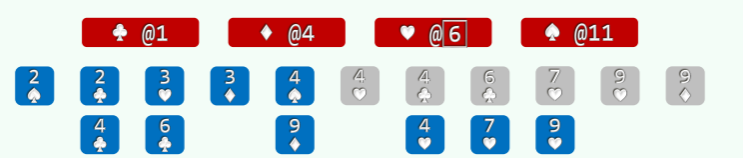
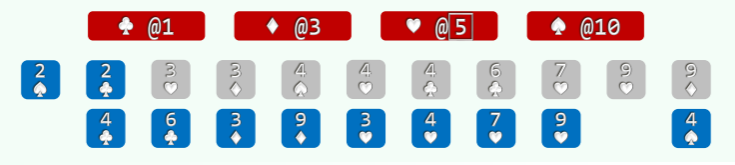
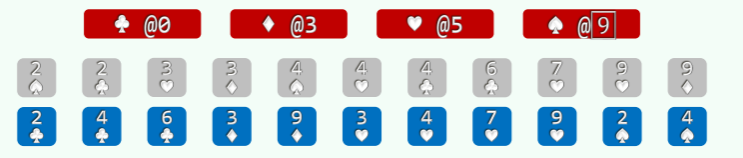
分析

时间复杂度=O (n+m+n) // 高效处理大规模数据
空间复杂度=O (n)
最后一步的扫描次序，可否改为自前向后？ ^dd99f2
- 可以
- 答案来自《算法导论》的习题 8-2-3：The algorithm still works correctly. The order that elements are taken out of C and put into B doesn’t affect the placement of elements with the same key. It will still fill the interval (C[k − 1], C[k]] with elements of key k.
- The question of whether it is stable or not is not well phrased. In order for stability to make sense, we would need to be sorting items which have information other than their key, and the sort as written is just for integers, which don’t. We could think of extending this algorithm by placing the elements of A into a collection of elements for each cell in array C. Then, if we use a FIFO collection, the modification of line 10 will make it stable, if we use LILO, it will be anti-stable.

跳转表

Skip lists are data structures that use probabilistic balancing rather than strictly enforced balancing.

Algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

结构

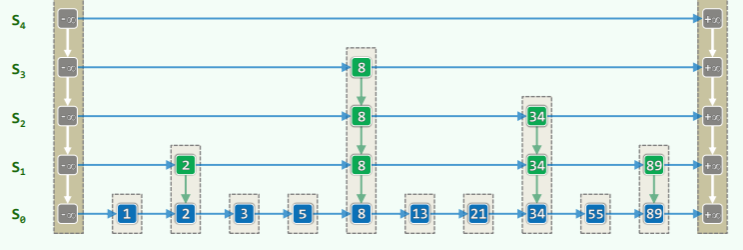
分层耦合的多个列表： $S_{0}, S_{1}, ..., S_{h}$ ， $S_{0}$ 是底层， $S_{h}$ 是顶层
横向为层 level: prev () , next () ，设有头尾哨兵
纵向成塔 tower: above (), below ()

实现

四联表

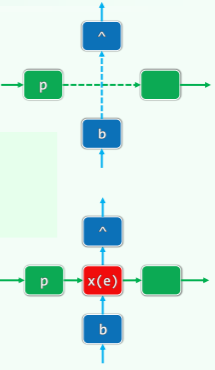
跳转表本身是四联表，由四联节点组成，四联节点指其左、右、上、下都有指针，分别为 x 的前驱、后继、上邻、下邻；

/***************************
 * QuadList interface
****************************/
template <typename T> struct Quadlist { //四联列表
	Rank _size; //规模
	QNodePosi<T> header, trailer; //头哨兵、尾哨兵
	void init(); //初始化
	int clear(); //清除所有节点
	Quadlist() { init(); } //构造
	~Quadlist() { clear(); delete header; delete trailer; } //析构
	T remove( QNodePosi<T> p ); //删除（合法）位置p处的节点，返回被删除节点的数值
	QNodePosi<T> insert( T const& e, QNodePosi<T> p, QNodePosi<T> b = NULL ); //将e作为p的后继、b的上邻插入
	void traverse( void (* ) ( T& ) ); //遍历各节点，依次实施指定操作（函数指针，只读或局部修改）
	template <typename VST> void traverse ( VST& ); //遍历
}; //Quadlist

/***************************
 * QuadNode implementation
****************************/
template <typename T> struct QNode;
template <typename T> using QNodePosi = QNode<T>*; //跳转表节点位置
template <typename T> struct QNode { //四联节点
	T entry; //所存词条
	QNodePosi<T> pred, succ, above, below; //前驱、后继、上邻、下邻
	QNode( T e = T(), QNodePosi<T> p = NULL, QNodePosi<T> s = NULL,QNodePosi<T> a = NULL, QNodePosi<T> b = NULL ) //构造器
      : entry( e ), pred( p ), succ( s ), above( a ), below( b ) {}
	QNodePosi<T> insert( T const& e, QNodePosi<T> b = NULL ); //将e作为当前节点的后继、b的上邻插入
};
template <typename T> QNodePosi<T> //将e作为当前节点的后继、b的上邻插入Quadlist
QNode<T>::insert( T const& e, QNodePosi<T> b ) {
	QNodePosi<T> x = new QNode<T>( e, this, succ, NULL, b ); //创建新节点
	succ->pred = x; succ = x; //设置水平逆向链接
	if ( b ) b->above = x; //设置垂直逆向链接
	return x; //返回新节点的位置
}

/***************************
 * QuadList::init()
****************************/
template <typename T> void Quadlist<T>::init() { //Quadlist初始化，创建Quadlist对象时统一调用
   header = new QNode<T>; //创建头哨兵节点
   trailer = new QNode<T>; //创建尾哨兵节点
   header->succ = trailer; header->pred = NULL; //沿横向联接哨兵
   trailer->pred = header; trailer->succ = NULL; //沿横向联接哨兵
   header->above = trailer->above = NULL; //纵向的后继置空
   header->below = trailer->below = NULL; //纵向的前驱置空
   _size = 0; //记录规模
} //如此构造的四联表，不含任何实质的节点，且暂时与其它四联表相互独立

/***************************
 * QuadList::insert()
****************************/
template <typename T> QNodePosi<T> //将e作为p的后继、b的上邻插入Quadlist
Quadlist<T>::insert( T const& e, QNodePosi<T> p, QNodePosi<T> b )
{ _size++; return p->insert( e, b ); } //返回新节点位置（below = NULL）

/***************************
 * QuadList::traverse()
****************************/
template <typename T> //遍历Quadlist，对各节点依次实施visit操作
void Quadlist<T>::traverse( void ( *visit )( T& ) ) { //利用函数指针机制，只读或局部性修改
	QNodePosi<T> p = header;
	while ( ( p = p->succ ) != trailer ) visit( p->data );
}

template <typename T> template <typename VST> //遍历Quadlist，对各节点依次实施visit操作
void Quadlist<T>::traverse( VST& visit ) { //利用函数对象机制，可全局性修改
	QNodePosi<T> p = header;
	while ( ( p = p->succ ) != trailer ) visit( p->data );
}

/***************************
 * QuadList::remove()
****************************/
template <typename T> //删除Quadlist内位置p处的节点，返回其中存放的词条
T Quadlist<T>::remove( QNodePosi<T> p ) { // assert: p为Quadlist中的合法位置
   p->pred->succ = p->succ; p->succ->pred = p->pred; _size--;//摘除节点
   T e = p->entry; delete p; //备份词条，释放节点
   return e; //返回词条
}

/***************************
 * QuadList::clear()
****************************/
template <typename T>
int Quadlist<T>::clear() { //清空Quadlist
	int oldSize = _size;
	while ( 0 < _size )
		remove( header->succ ); //逐个删除所有节点
	return oldSize;
}

跳转表

由此，构建跳转表：

/***************************
 * SkipList interface
****************************/
#include "List/List.h" //引入列表
#include "Entry/Entry.h" //引入词条
#include "Quadlist.h" //引入Quadlist
#include "Dictionary/Dictionary.h" //引入词典

template <typename K, typename V> //key、value
//符合Dictionary接口的Skiplist模板类（隐含假设元素之间可比较大小）
struct Skiplist : public Dictionary<K, V>, public List< Quadlist< Entry<K, V> >* > {
   Skiplist() { insertAsFirst( new Quadlist< Entry<K, V> > ); }; //即便为空，也有一层空列表
   QNodePosi< Entry<K, V> > search( K ); //由关键码查询词条
   Rank size() const { return empty() ? 0 : last()->data->_size; } //词条总数
   Rank height() { return List::size(); } //层高 == #Quadlist
   V* get( K ); //读取
   bool put(K, V); //插入（Skiplist允许词条重复，故必然成功）
   bool remove ( K ); //删除
};

/***************************
 * SkipList::get()
 * 读取词条
****************************/
template <typename K, typename V>
V* Skiplist<K, V>::get( K k ) {
	QNode< Entry<K, V> >* p = search(k); //无论是否命中，search()都不会返回NULL
	return (p->pred && p->entry.key == k) ? &(p->entry.value) : NULL; //故须再做判断
} //有多个命中时靠后者优先

空间性能

逐层随机减半： $S_{k}$ 中每个关键码，在 $S_{k + 1}$ 中出现的概率均为 1/2
因此各塔的高度符合几何分布： $P r (h = k) = p^{k - 1} \cdot (1 - p)$
于是塔高的期望： $E (h) = \frac{1}{1 - p} = 2$
更直观的解释：
- 既然逐层随机减半，故 $S_{0}$ 中任意关键码在 $S_{k}$ 中仍然出现的概率为 $2^{- k}$ ，则第 k 层节点数的期望值 $E (∣ S_{k} ∣) = n \cdot 2^{- k} = \frac{n}{2 ^{k}}$
- 于是所有节点期望的总数——各层列表所需空间的总和为 $E (k \sum ∣ S_{k} ∣) = k \sum E (∣ S_{k} ∣) = n \times k \sum 2^{- k} < 2 n = O (n)$
- 于是，跳转表的所需空间为 expected-O (n)，不会因为塔高而显著影响空间复杂度
- 类比，半衰期为 1 年的放射性物质中，各粒子的平均寿命不过 2 年

查找

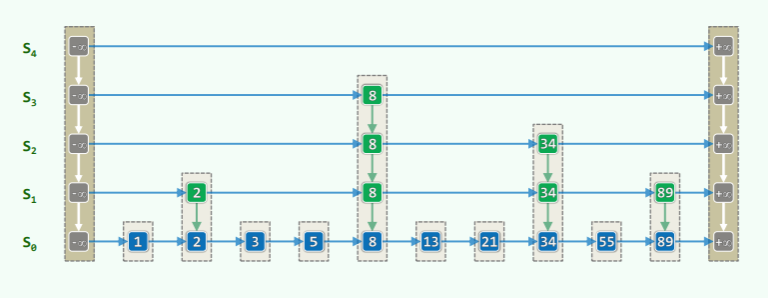
减治思路——由高到低，类似二分查找

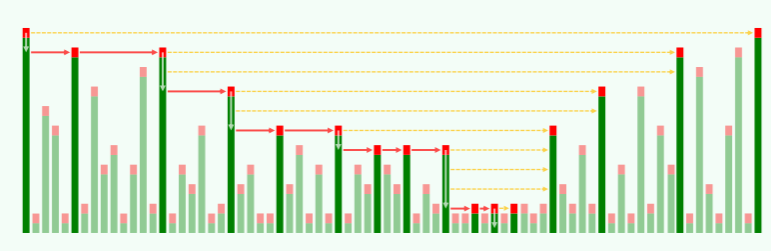
查找时间取决于横向、纵向累积的跳转次数，因此考察跳转次数：
纵向跳转次数（塔高，最坏情况）：
- 观察得知，一座塔的高度不低于 k (层数) 的概率为 p^k，因此随着 k 的增加， $S_{k}$ 为空的概率急剧上升： $P r (∣ S_{k} = 0∣) = (1 - p^{k})^{n} \geq 1 - n \cdot p^{k}$
- 由此可知，跳转表高度 h=O (logn)的概率极大
- 举例，若 p=1/2，则 $k = 3 \cdot lo g_{\frac{1}{p}} n$ 层非空的概率为 $P r (∣ S_{k} ∣ > 0) \leq n \cdot p^{k} = n \cdot n^{- 3} = \frac{1}{n ^{2}} \sim 0$
- 因此，查找过程中，纵向跳转的次数累计不超过 expected-O (logn)
横向跳转次数（）：
- 观察得知：横向跳转所经的节点必然依次紧邻，而且每次抵达都是塔顶
- 于是将沿同一层列表跳转的次数记作 Y，则符合几何分布 $P r (Y = k) = (1 - p)^{k}$
- 几何分布的期望为 $E (Y) = \frac{1 - p}{p} = \frac{1 - 0.5}{0.5} = 1$ 次, 即同一层列表中连续跳转的期望时间成本 = 1次跳转 + 1次驻足 = 2
故跳转表的每次查找，都可在 expected-(2h)=expected-O (logn)时间内完成

/***************************
 * SkipList::search()
 * 返回关键码不大于k的最后一个词条（所对应塔的基座）
****************************/
template <typename K, typename V>
QNodePosi<Entry<K, V>> Skiplist<K, V>::search(K k ) {
	for ( QNodePosi<Entry<K, V>> p = first()->data->header; ; ) //从顶层Quadlist的首节点p出发
	    if ( ( p->succ->succ ) && ( p->succ->entry.key <= k ) ) p = p->succ; //尽可能右移
	    else if ( p->below ) p = p->below; //水平越界时，下移
	    else return p; //验证：此时的p符合输出约定（可能是最底层列表的header）
}

插入与删除

/***************************
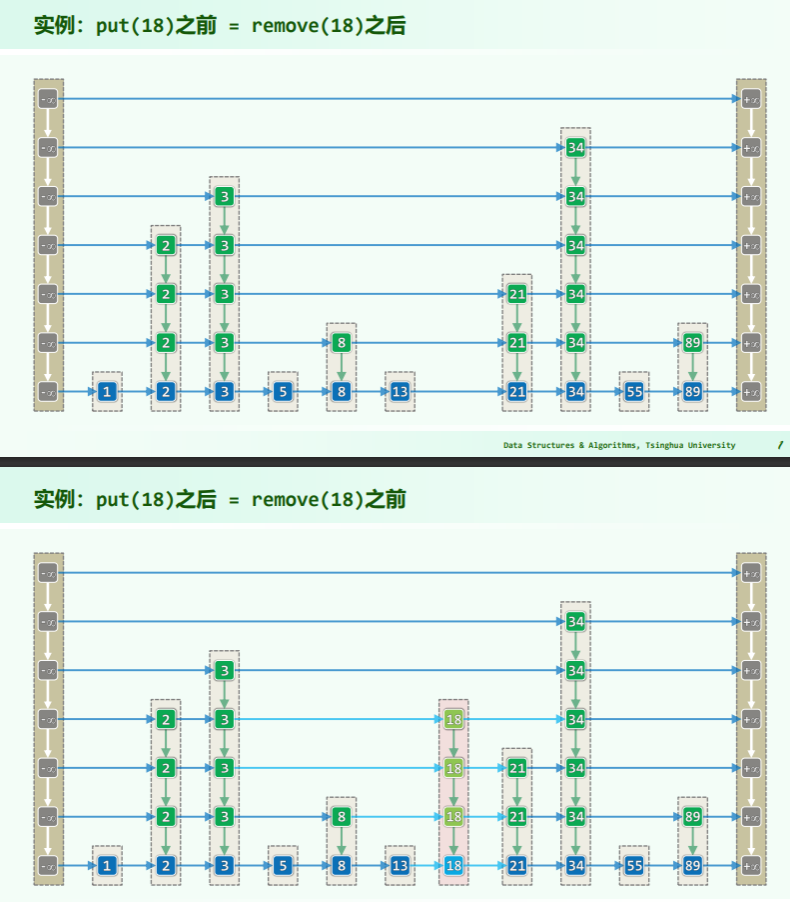
 * SkipList::put()
 * 插入词条(SkipList允许词条重复，故必然成功)
****************************/
template <typename K, typename V>
bool Skiplist<K, V>::put( K k, V v ) { 
	Entry<K, V> e = Entry<K, V>( k, v ); //待插入的词条（将被同一塔中所有节点共用）
	QNodePosi< Entry<K, V> > p = search( k ); //查找插入位置：新塔将紧邻其右，逐层生长
	ListNodePosi< Quadlist< Entry<K, V> >* > qlist = last(); //首先在最底层
	QNodePosi< Entry<K, V> > b = qlist->data->insert( e, p ); //创建新塔的基座
	while ( rand() & 1 ) { //经投掷硬币，若确定新塔需要再长高，则
	    while ( p->pred && !p->above ) p = p->pred; //找出不低于此高度的最近前驱
		if ( !p->pred && !p->above ) { //若该前驱是header，且已是最顶层，则
			insertAsFirst( new Quadlist< Entry<K, V> > ); //需要创建新的一层
			first()->data->header->below = qlist->data->header;
			qlist->data->header->above = first()->data->header;
		}
	    p = p->above; qlist = qlist->pred; //上升一层，并在该层
	    b = qlist->data->insert( e, p, b ); //将新节点插入p之后、b之上
	} //课后：调整随机参数，观察总体层高的相应变化
	return true; //Dictionary允许重复元素，插入必成功
}

/***************************
 * SkipList::remove()
 * 删除词条
****************************/
template <typename K, typename V>
bool Skiplist<K, V>::remove( K k ) { 
	QNodePosi< Entry<K, V> > p = search ( k ); //查找目标词条
	if ( !p->pred || (k != p->entry.key) )  return false; //若不存在，直接返回
	ListNodePosi< Quadlist< Entry<K, V> >* > qlist = last(); //从底层Quadlist开始
	while ( p->above ) { qlist = qlist->pred; p = p->above; } //升至塔顶
	do { //逐层拆塔
	    QNodePosi< Entry<K, V> > lower = p->below; //记住下一层节点，并
	    qlist->data->remove( p ); //删除当前层节点，再
	    p = lower; qlist = qlist->succ; //转入下一层
	} while ( qlist->succ ); //直到塔基
	while ( (1 < height()) && (first()->data->_size < 1) ) { //逐层清除
	    List::remove( first() ); 
	    first()->data->header->above = NULL;
	} //已不含词条的Quadlist（至少保留最底层空表）
	return true; //删除成功
}

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索