C0-Nonlinear-Transformation

Quadratic Hypotheses

之前我们学习了线性模型，但是对于一些问题，任何线性模型产生的 $E_{in}$ 都大得难以接受，我们不得不考虑非线性模型：

• 以圆形模型为例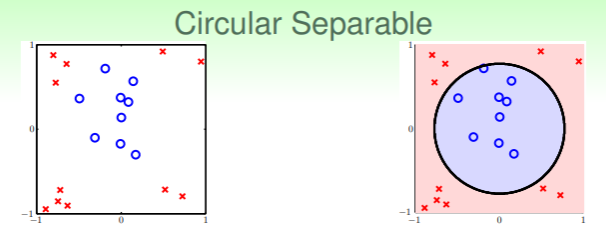： 这个数据集是圆形可分的，其分类函数为 $h_{CircSEP}(\mathbf{x})=\text{sign}(-x_1^2-x_2^2+0.6)$

Circular Separable to Linear Separable

如果对这个圆形模型再像之前的探讨一样做一遍 circular-PLA、circular-Regression… 未免太过笨拙，我们考虑化非线性为线性，从而直接套用之前的线性分类器：

• 考虑圆形分类函数的各项含义，我们可以分离出权重和各维变量：$h(\mathbf{x})=\text{sign}\left(\underset{{\tilde{w}}_0}{\underbrace{0.6}}\cdot \underset{z_0}{\underbrace{1}}+\underset{{\tilde{w}}_1}{\underbrace{(-1)}}\cdot \underset{z_1}{\underbrace{x_1^2}}+\underset{{\tilde{w}}_2}{\underbrace{(-1)}}\cdot \underset{z_2}{\underbrace{x_2^2}}\right)=\text{sign}\left({\tilde{\mathbf{w}}}^T\mathbf{z}\right)$ ，将平方项用一次项代替，我们就又得到了线性模型；
• 这实现了从 圆形可分$\{({\mathbf{x}}_n,y_n)\}$ 到 线性可分$\{({\mathbf{z}}_n,y_n)\}$ 的转换，在 ML 中称这样的转换为特征转换（ feature transform, denoted as $\Phi$ ）：$\mathbf{x}\in \mathcal{X}\stackrel{\Phi }{\mapsto }\mathbf{z}\in \mathcal{Z}$
• 

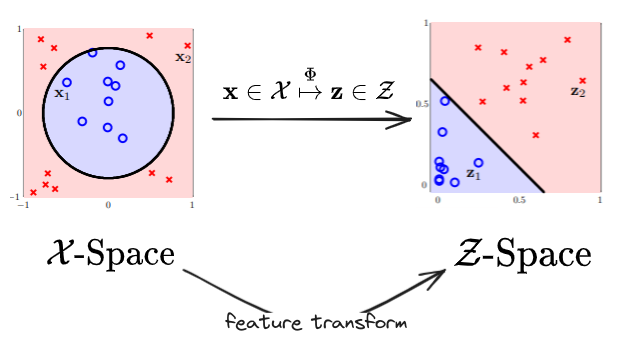
Linear Separable to Circular Separable

从二维的圆形可分转换到线性可分是可行的，那么反过来，还能从线性可分转换成圆形可分吗？

• 写成数学语言，就是对线性特征向量 $\mathbf{z}=(z_0,z_1,z_2)$ 经过特征转换得到 $\Phi (\mathbf{x})=\Phi (1,x_1^2,x_2^2)$ ，是否有假设函数能实现：$h(\mathbf{x})=\tilde{h}(\mathbf{z})=\text{sign}\left({\tilde{\mathbf{w}}}^T\Phi (\mathbf{x})\right)=\text{sign}\left(\widetilde{w_0}+\widetilde{w_1}{x}_1^2+\widetilde{w_2}{x}_2^2\right)$ ？
• 结合解析几何，我们对不同的权重向量 $\tilde{\mathbf{w}}=(\widetilde{w_0},\widetilde{w_1},\widetilde{w_2})$ ，实际上可以得出以下的线性到非线性的转换：
• 不过显然，我们这里实现的转换其实是在 $\mathcal{Z}$ 空间中的直线对 $\mathcal{X}$ 空间中特定二次曲线的转换，而不是任意的转换都能实现；这是由于维度限制的；

如果想实现任意直线到二次曲线的转换，我们需要扩充转换函数的维度：${\Phi }_2(\mathbf{x})=(1,x_1,x_2,x_1^2,x_1{x}_2,x_2^2)$ ，经过这样转换后的假设集才能包含全部的二维空间的曲线：${\mathcal{H}}_{{\Phi }_2}=\left\{h(\mathbf{x}):h(\mathbf{x})=\tilde{h}({\Phi }_2(\mathbf{x}))\text{ for some linear }\tilde{h}\text{ on }\mathcal{Z}\right\}$ 。

试看下面这个例子，对于一个偏心椭圆 $2(x_1+x_2-3{)}^2+(x_1-x_2-4{)}^2=1$ ，其可以通过 ${\tilde{\mathbf{w}}}^T{\Phi }_2(\mathbf{x})$ 实现，其中 ${\tilde{\mathbf{w}}}^T=[33,-20,-4,3,2,3]$ 。

站在二次曲线的角度，我们可以将线性直线看作是其中的特例，即二次项的系数全部为 0 。

练习：熟悉曲线到直线的转换

Nonlinear Transform

现在，一切真相大白：

• 只要我们能够实现特征转换，那么在线性模型上的假设就可以应用到非线性模型，并且这样的转换实质上只是符号的转换，而不会带来精度的影响：

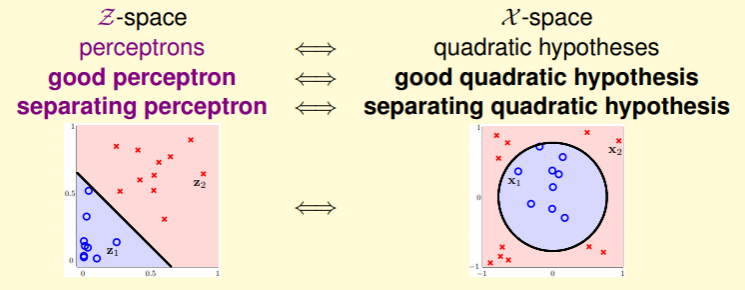
Nonlinear Perceptron to Linear Perceptron

只要将数据也经过同样的转换，那么在 $\mathcal{Z}$ 空间中的好的线性感知器在经过特征转换后，就是在 $\mathcal{X}$ 空间中同样优秀的非线性感知器，具体步骤如下：

1. 将原始非线性数据 $\{({\mathbf{x}}_n,y_n)\}$ 通过特征转换 $\Phi$ 转换为线性数据 $\{({\mathbf{z}}_n,y_n)\}$ ；
2. 在 $\mathcal{Z}$ 空间中使用合适的线性模型 $\mathcal{A}$（如：PLA、pocket、Linear Regression、Logistic Regression）获取一个足够好的感知器 $\tilde{\mathbf{w}}$ ；
3. 返回的最佳估计为 $g(\mathbf{x})=\text{sign}({\tilde{\mathbf{w}}}^T\Phi (\mathbf{x})$ ；

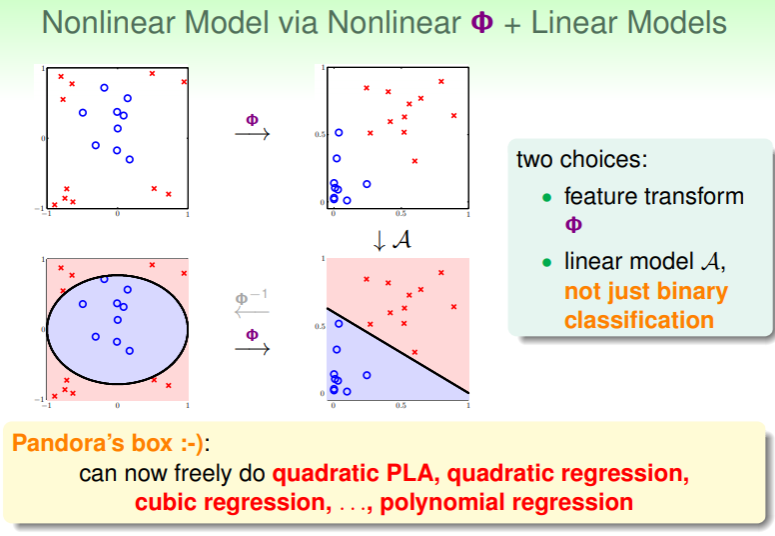现在，我们完成了思路的梳理，余下最关键的就是特征转换如何找到了。

在探讨特征转换之前，考虑之前谈论过的一个例子，第三节我们讨论过将 手写数字的像素图转换为二维图 的例子：

• 
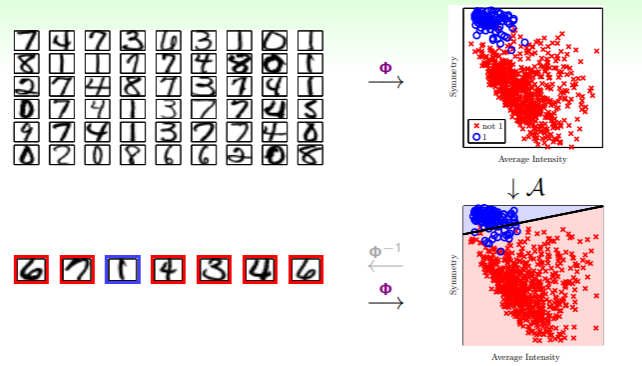
• 这里我们将 $16\times 16$ 的 256 维的数字像素图，进行特征转换（提取）后，得到可以二元分类的两个特征——密度、对称性；

练习：特征转换的维度变化

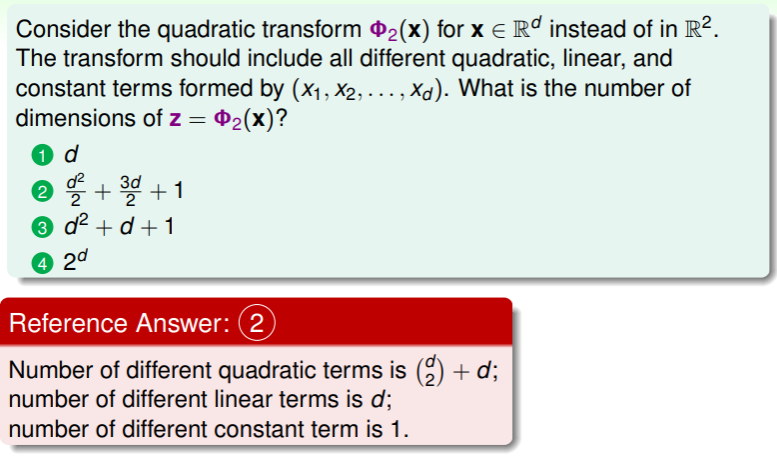
Price of Nonlinear Transform

根据上面的论证，我们可以推知，要实现从 d 维空间降维到 Q 维空间，我们需要的特征转换函数为：

$$\begin{array}{rl}{\Phi }_Q(\mathbf{x})=(& 1,\\ & x_1,x_2,...,x_d,\\ & x_1^2,x_1{x}_2,...,x_d^2,\\ & ...,\\ & x_1^Q,x_1^{Q-1}{x}_2,...,x_d^Q)\end{array}$$

这是一个 Q 次多项式的转换，其中的维数是 $\underset{\widetilde{w_0}}{\underbrace{1}}+\underset{\text{others}}{\underbrace{\tilde{d}}}$ 个，其数量就是小于 Q 次方的所有组合的数量：$\left(\genfrac{}{}{0ex}{}{Q+d}{Q}\right)=\mathcal{O}(Q^d)$ ，这意味着在从非线性的 $\mathcal{X}$ 空间转换到线性的 $\mathcal{Z}$ 空间时，$\mathbf{z}={\Phi }_Q(\mathbf{x})$ 耗费的时间和 $\tilde{\mathbf{w}}$ 耗费的空间都是 $\mathcal{O}(Q^d)$ 。

另一方面，从 VC Dimension 的角度来看，$\tilde{\mathbf{w}}=1+\tilde{d}$ 所代表的自由度（VC Dimension 的维数）也大概是 $d_{VC}({\mathcal{H}}_{{\Phi }_Q})$ ，不过还好，由于 $\mathcal{Z}$ 空间中任何超过 $1+\tilde{d}$ 维的输入都不会被 shatter，因此 $d_{VC}({\mathcal{H}}_{{\Phi }_Q})\le 1+\tilde{d}$ ，并且 $\mathcal{X}$ 空间中也不会 shatter 超过 $1+\tilde{d}$ 维的输入（$\mathcal{X}$ 空间这个当结论记住，比较难证，林老师也没有详说）

总之，Q 越大，代表着实现转换时的时间复杂度和空间复杂度越大，相应的 $d_{VC}$ 也会越大。

Overfitting Risk

如何权衡 Q 呢？试看这个分类：

• 
• 相对于一次曲线的分类，四次曲线的分类虽然 $E_{in}=0$，但是显然我们认为它把噪声也额外地进行了分类，这是不合理的，称为 overkill 或 overfit

综合起来，我们这里有两个问题：

1. 我们在何种程度上确保 $E_{out}$ 足够接近 $E_{in}$ 呢？
2. 我们在何种程度上确保 $E_{in}$ 足够小呢？

这两个问题不可兼得，是 ML 中一个关键的 trade-off（权衡），满足一者必然要适当的放宽另一者。

Danger of Visual Choices

另外一个问题是，选择降维到的 Q 如何抉择？考虑降维到二维空间：

• 
• 先前我们讨论过完全实现降维需要特征转换是 6 维的，但是视觉上我们似乎用 3 维的圆也可以实现分类？进一步，我们也许可以提出 2 维、1 维的特征转换也能够实现这样的目标？不过这样的操作很危险，因为这是我们人工地对部分数据进行了 Human Learning ，我们用自己的学识、偏见做出了不一定合理的降维，这在更大范围的数据上并不一定可行，甚至可能导致结果和预期偏离甚远。
• Human Learning 不能代替 Machine Learning ，Human Learning 的操作在局部上是比 ML 更“聪明、敏捷”的，因此如果过分的依赖 Human Learning ，就会对 ML 模型的性能估计得过于乐观；
• 事实上，三维以上的空间就很难 visualize ，因此 visualize 这种手段是不可靠、不可行的。

练习：降维的代价

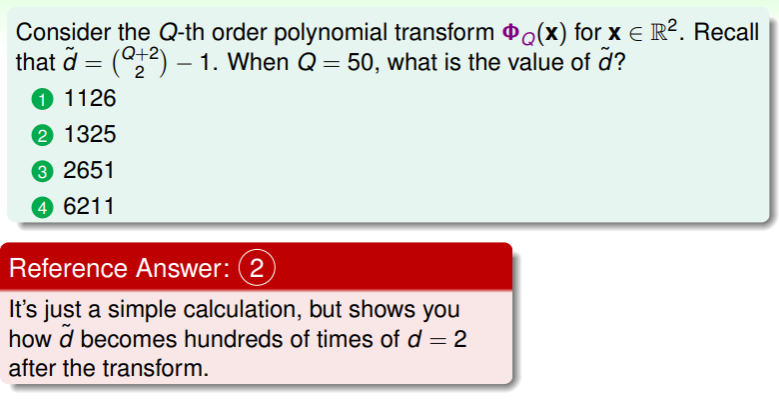
• 我们之前在 VC Dimension 中讨论过，要支撑 1300 多个维度的学习，我们至少需要 13000 个样本数据，这对数据集的大小要求颇高。

Structured Hypothesis Sets

重新站在特征转换的角度思考 $E_{in}$ 和 $E_{out}$ 的关系。

Nested Hypotheses Set

实现特征转换的函数可以写成如下嵌套的形式：

$$\begin{array}{rl}{\Phi }_0(\mathbf{x})& =(1)\\ {\Phi }_1(\mathbf{x})& =({\Phi }_0(\mathbf{x}),x_1,x_2,...,x_d)\\ {\Phi }_2(\mathbf{x})& =({\Phi }_1(\mathbf{x}),x_1^2,x_1{x}_2,...,x_d^2)\\ {\Phi }_3(\mathbf{x})& =({\Phi }_2(\mathbf{x}),x_1^3,x_1^2{x}_2,...,x_d^3)\\ & ...\\ {\Phi }_Q(\mathbf{x})& =({\Phi }_{Q-1}(\mathbf{x}),x_1^Q,x_1^{Q-1}{x}_2,...,x_d^Q)\end{array}$$

从假设集的角度来看，随着维度的增加，呈现集合包含的关系，即低维空间的变换是高维空间变化的特例：

• ${\mathcal{H}}_{{\Phi }_0}\subset {\mathcal{H}}_{{\Phi }_1}\subset {\mathcal{H}}_{{\Phi }_2}\subset {\mathcal{H}}_{{\Phi }_3}\subset ...\subset {\mathcal{H}}_{{\Phi }_Q}$
• nested ${\mathcal{H}}_i$ ：

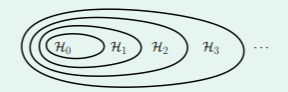
VC Dimension and Feature Transform

考虑假设的 VC Dimension 与 $E_{in}$ 的关系，则有：

• 首先，高维空间可以 shatter 的点一定比低维空间可以 shatter 的点更多： $d_{VC}({\mathcal{H}}_0)\le d_{VC}({\mathcal{H}}_1)\le d_{VC}({\mathcal{H}}_2)\le d_{VC}({\mathcal{H}}_3)\le ...$ ，
• 相应的，在考虑找到每个 ${\mathcal{H}}_i$ 最小的 $E_{in}$ 时，即 $g_i=arg{\min }_{h\in {\mathcal{H}}_i}{E}_{in}(h)$，就会有 $E_{in}(g_0)\ge E_{in}(g_1)\ge E_{in}(g_2)\ge E_{in}(g_3)\ge ...$ ，这是因为高维空间的可选范围更广了，因此找到更低的 $E_{in}$ 的假设 g 的概率也会下降；
• 因此这就从另一个角度解释这幅图：

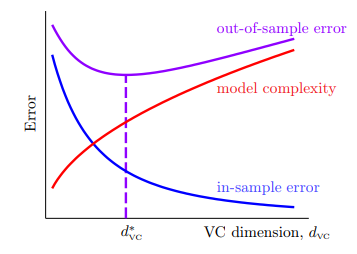
因此使用高维的特征转换尽管能够做到 $E_{in}\to 0$ ，但从全局来看并不意味着完美，因为一方面实现转换时的复杂度太高，另一方面 $E_{out}$ 却并不能像 $E_{in}$ 一样低。要明确，$E_{in}$ 只是一个中间产物，如果过于计较眼前的“得”，有可能导致全局的“失”。

安全的学习路线应当是从低维的假设集开始：${\mathcal{H}}_1\to {\mathcal{H}}_{\text{high}}$ ，如果 $E_{in}(g_1)$ 已经足够好，那自然皆大欢喜，否则逐步地增加转换的维度——从线性模型开始做起，逐步扩展到高维模型。

练习：理解 VC Dimension 与特征转换