判断
- ( ✅ ) f(n) = O(g(n)),当且仅当 g(n) = Ω(f(n))。
- ( ❌ )若借助二分查找确定每个元素的插入位置,向量的插入排序只需 O(nlogn)时间。
- ( ❌ )无论有序向量或有序列表,最坏情况下均可在 O(logn)时间内完成一次查找。
- ( ✅ )对有序向量做 Fibonacci 查找,就最坏情况而言,成功查找所需的比较次数与失败查找相等。
- ( ❌ )只要是采用基于比较的排序算法,对任何输入序列都至少需要运行 Ω(nlogn) 时间。
- ( ✅ )对不含括号的中缀表达式求值时,操作符栈的容量可以固定为某一常数。
- ( ❌ )对于同一有序向量,每次折半查找绝不会慢于顺序查找。
- ( ✅ )RPN 中各操作数的相对次序,与原中缀表达式完全一致。
答案全部正确 6题所谓常数,其实就是 , ,
^这三个不同优先级的运算符。
多项选择
- ( C, D )若 f (n) = O (n^2) 且 g (n) = O (n),则以下结论正确的是: A. f(n) + g(n) = O(n^2) B. f(n) / g(n) = O(n) C. g(n) = O(f(n)) D. f(n) * g(n) = O(n^3)
❌ 正确答案是:A, D
- ( A, B )算法 g (n)的复杂度为 Θ(n)。若算法 f (n)中有 5 条调用 g (n)的指令,则 f (n)的复杂度为: A. Θ(n) B. O(n) C. Ω(n) D.不确定
❌ 正确答案:D。可以参考习题解析 1-7 ,构造恒假的分支语句屏蔽掉这五个 g
- ( C )共有几种栈混洗方案,可使字符序列{‘x’, ‘o’, ‘o’, ‘o’, ‘x’}的输出保持原样? A. 12 B. 10 C. 6 D. 5
✅
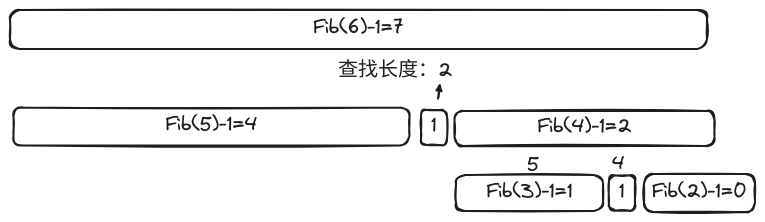
- ( C )对长度为 Fib (12) ‐ 1 = 143 的有序向量做 Fibonacci 查找,比较操作的次数至多为: A. 12 B. 11 C. 10 D. 9
❌ 正确答案是:B 对该长度的向量进行 Fibonacci 查找,则第一步的划分后,得到的向量有三个区间,长度分别为:Fib (11)-1, 1 (即 mi), Fib (10)-1。 由于 Fibonacci 查找的特点——最坏情况时,失败查找和成功查找进行的比较次数相同,并且向右深入分支的代价是 2。因此考察原向量 (mi, hi)这一区间,即再次对 Fib (10)-1 长度的向量区间进行划分,得到 Fib (9)-1, 1 (new mi), Fib (8)-1 三个长度的新的向量划分。 以此类推,直到左子向量长度为 Fib (3)-1=1 时,其即是最多需要比较次数的元素。示意图如下:
- ( B, C )对长度为 n = Fib (k) ‐ 1 的有序向量做 Fibonacci 查找。若各元素的数值等概率独立均匀分布,且平均成功查找长度为 L,则平均失败查找长度为: A. n(L‐1)/(n‐1) B. n(L+1)/(n+1) C. (n‐1)L/n D. (n+1)L/n
❌ B 习题解析 2-18:二分搜索的平均查找长度
复杂度分析
给出函数F(n)复杂度的紧界(假定int字长无限,移位属基本操作,且递归不会溢出)
void F(int n) //O( loglogn ) ✅
{ for (int i=1,r=1; i<n;i<<r,r<<=1);}
void F(int n) //O( √n ) ✅
{ for (int i=0, j=0; i<n;i+=j,j++;}
void F(int n) //O( log*n ) ✅
{ for (int i=1; i<n;i=1<<i);}
void F(int n) //O( logn ) ❌ O(n^0.694)
{ return (n<4)? n: F(n>>1) + F(n>>2); }
int F(int n) //O( n^2 ) ❌ O(2^n)
{ return (n == 0) ? 1 : G(2, F(n‐1)); }
int G(int n, int m)
{ return (m == 0) ? 0 : n + G(n,m‐1); }
int F(int n) //O( n^2 ) ✅
{ return G(G(n‐1)); }
int G(int n) { return (n==0) ? 0 : G(n‐1) + 2*n ‐ 1; }
void F(int n) { //O( nlogn ) ✅
for (int i=1; i<n;i++)
for (int j=0; j<n;j+=i);
}
void F(int n) { //expected‐O( nlogn ) ✅
for (int i=n; 0<i; i--)
if(0 == rand()%i)
for(int j=0;j<n;j++);
}
简答题
- 考查如下问题:任给 12 个互异的整数,且其中 10 个已组织为一个有序序列,现需要插入剩余的两个以完成整体排序。若采用基于比较的算法(CBA),最坏情况下至少需做几次比较?为什么?
最坏需要做 11+12 次比较,这种情况是第 11、12个元素分别搜索整个序列后才找到自己的位置。
❌ 习题 2-39 前一整数可能的插入位置数 * 后一整数可能的插入位置数 = 11 * 12 = 132 这也是该判定树应含叶节点数目的下限。 于是对应地,判定树的高度应至少是: 这也是此类算法在最坏情况下需做比较操作次数的下限。
- 向量的插入排序由 n 次迭代完成,逐次插入各元素。为插入第 k 个元素,最坏情况需做 k 次移动,最好时则无需移动。从期望的角度来看,无需移动操作的迭代平均有多少次?为什么? 假定各元素是等概率独立均匀分布的。
无需移动就是插入在序列末尾,在插入元素的过程中,这一概率为 1,1/2,1/3,1/4…,因此整体期望为
✅
- 现有长度为 15 的有序向量
A[0.. 14],各元素被成功查找的概率如下:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1/128 | 1/128 | 1/32 | 1/8 | 1/8 | 1/32 | 1/16 | 1/16 | 1/128 | 1/64 | 1/16 | 1/4 | 3/16 | 1/128 | 1/64 | |
| 若采用二分查找算法,试计算该结构的平均成功查找长度。 |
✅
- 考查表达式求值算法。算法执行过程中的某时刻,若操作符栈中的括号多达 2010 个,则此时栈的规模(含栈底的’\0’)至多可能多大?试说明理由,并示意性地画出当时栈中的内容。
(2010+1)*4+1 = 8045个字符,栈中内容是:\0+*^(+*^(+*^(...(+*^(+*^!,其中 和 可以用相同优先级的运算符 或 代替。
✅
- 阅读以下程序,试给出其中 ListReport ()一句的输出结果(即当时序列 L 中各元素的数值)
#define LLIST_ELEM_TYPE_INT //节点数据域为int型
LValueType visit(LValueType e) {
static int lemda = 1980;
lemda += e*e;
return lemda;
}
int main(int argc, char* argv[]) {
LList* L = ListInit(‐1);
for (int i=0; i<5; i++)
ListInsertFirst(L, i);
ListTraverse(L, visit);
ListReport(L); /*输出: */
ListDestroy(L);
return 0;
}
1996 2005 2009 2010 2010 ✅
算法题
- sortOddEven (L)
#define LLIST_TYPE_ARRAY //基于向量实现序列
#define LLIST_ELEM_TYPE_INT //节点数据域为 int 型
/************************************************************************
* 输入:基于向量实现的序列 L
* 功能:移动 L 中元素,使得所有奇数集中于前端,所有偶数都集中于后端
* 输出:无
* 实例:L = {2, 13, 7, 4, 6, 3, 7, 12, 9},则排序后
* L = {9, 13, 7, 7, 3, 6, 4, 12, 2}
* 要求:O(n)时间,O(1)附加空间 ************************************************************************/
void sortOddEven(LList* L) { }
快排的快速划分思想
- shift (L, k)
#define LLIST_TYPE_ARRAY //基于向量实现序列
#define LLIST_ELEM_TYPE_INT //节点数据域为 int 型
/************************************************************************
* 输入:基于向量实现的序列 L
* 功能:将 L 中各元素循环左移 k 位
* 输出:无
* 实例:L = {1,..., k, k+1, ..., n},则左移后
* L = {k+1, ..., n, 1, ..., k}
* 要求:O(n)时间(注意:最坏情况下 k=Ω(n)),O(1)附加空间 ************************************************************************/
void shift(LList* L, int k) {
// Assert: L != NULL, 0 < k < Length(L)
}