2014-final

判断

由同⼀组共 n 个词条构成的任意两棵 BST，经 O(logn)次 zig 或 zag 旋转之后，必定可以相互转换。

❌ 需要 $O (n)$ 次。

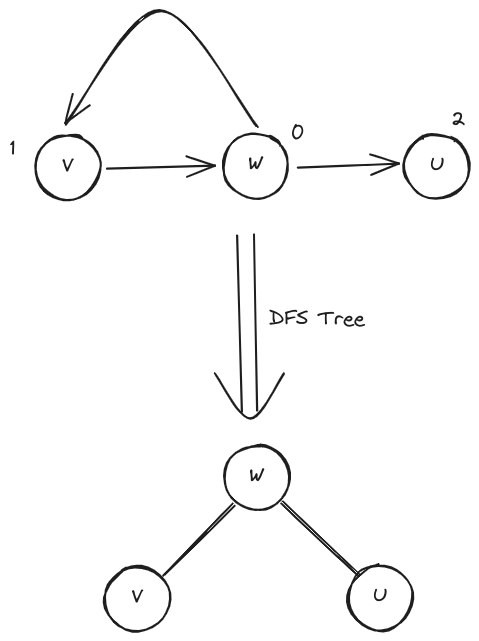
设在有向图 G 中，存在⼀条⾃顶点 v 通往 u 的路径。于是，若在某次 DFS 中有 dTime(v) < dTime(u)，则这次 DFS 所⽣成的 DFS 森林中，v 必定是 u 的祖先。

❌

[! warning] 勿要混淆！ G 是有向无环图，(v, u) 是其中一条由 v 指向 u 的边，对 G 做 DFS 的结果中，可以得到 v 和 u 的 dTime 关系或 fTime 关系是： A. dTime (v) > dTime (u) B. dTime (v) < dTime (u) C. fTime (v) > fTime (u) D. fTime (v) < fTime (u)

答案正解是 C。

在⽆向连通图 G 中选定⼀个顶点 s，并将各顶点 v 到 s 的距离记作 dist(v)（特别地，dist(s)=0）。于是在G.Bfs(s)过程中，若辅助队列为 Q，则 dist(Q.front()) + 1 >= dist(Q.rear()) 始终成⽴。

✅ 层次遍历的高度差始终不会超过 1。

我们知道，因同⼀顶点的邻居被枚举的次序不同，同⼀有向图 G 所对应的 DFS 森林未必唯⼀。然⽽只要起始于 G 中某顶点 s 的某次 DFS 所⽣成的是⼀棵树，则起始于 s 的任何⼀次 DFS 都将⽣成⼀棵树。

✅ 零入度拓扑排序做理解。只有零入度的点开始 DFS 才可以在一个强连通分量中到达所有节点。

⽆论 g 和 h 互素与否，已经 h-sorted 的序列再经 g-sorting 之后，必然继续保持 h-sorted。

✅ shellSort 的基本原理。

在 BM 算法中，对于任⼀模式串 P，0 < gs(j) ⇐ j 对于每个0 ⇐ j < |P| 都成⽴。

❌ 初始化时 gs[] 中所有元素都设置为 |P|。

相对于⼆叉堆，尽管多叉堆的⾼度更低，但⽆论是下滤⼀层还是整个下滤过程，时间成本反⽽都会增加。

✅ 正确答案：❌ 对于三叉堆，下滤成本降低，对于四叉堆，下滤成本保持不变，但考虑到缓存等问题，实际效率高于二叉堆。

我们知道，采取双向平⽅试探策略时，应该将散列表取作素数 M = 4k + 3。尽管这样可以极⼤降低查找链前 M 个位置发⽣冲突的概率，但仍不能杜绝。

❌ 可以杜绝。

即便访问序列不满⾜局部性（⽐如完全理想的随机），伸展树依然能够保证分摊 O(logn) 的性能。

✅

我们知道，BTree::solveOverflow() 和 BTree::solveUnderflow() 在最坏情况下均需 Ω(logn) 的时间，然⽽在 BTree 任意⾜够⻓的⽣命期内，就分摊意义⽽⾔⼆者都仅需要 O(1) 时间。

❌

✅ 习题 8-6：BTree 节点插入过程中导致的分裂次数的分析。分裂和合并的最坏情况也不过 $Ω (lo g_{m} N)$ ，因此分摊下来就是 $O (1)$

选择

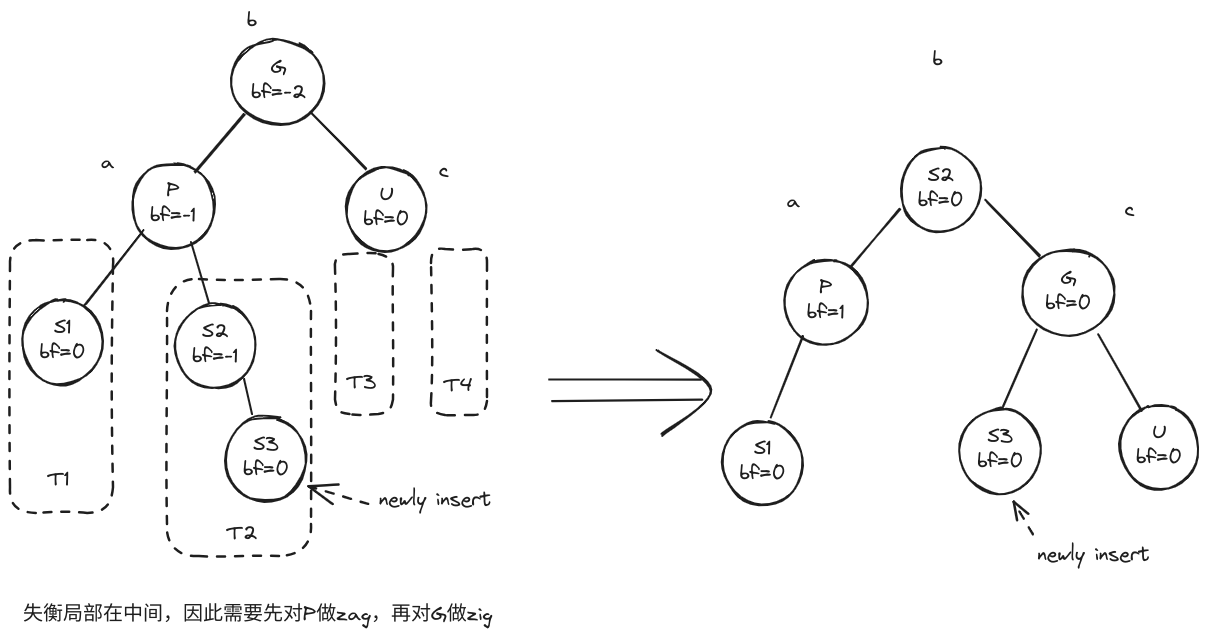
设在某新节点插⼊AVL 树后（尚待平衡化时），最低失衡节点为 g。若此时 g 的左、右孩⼦的平衡因⼦分别为-1，0，则应通过（ C ）旋转使之重新恢复平衡。 A）zig； B）zig+zag； C）zag+zig； D）zag； E）不确定

失衡局部处于中间。

为从2014个随机元素中挑选出最⼤的5个，（ A ）在最坏情况下所需的⽐较操作次数最少。 A）构建⼤顶的锦标赛树，再做5次 delMax()； B）⽤Floyd 算法构建⼤顶堆，再做5次 delMax()； C）采⽤选择排序算法，但仅执⾏前5次迭代； D）采⽤起泡排序算法，但仅执⾏前5次迭代； E）⽤linearSelect()算法找出第5⼤的元素，再遍历⼀趟找出（⾄多）4个⼤于它的元素

A. 胜者树在构建时需要 1007 次比较，在 delMax 后恢复时，至多需要 $5 \times 11 \times 2 = 110$ 次比较。总共至多 1117 次比较。 B. 比较次数：构建时 $O (n)$ 量级的比较，而 5次 delMax() 需要 $O (5 lo g n)$ 次比较 C. 2013+2012+2011+2010+2009=10055 D. 2013+2012+2011+2010+2009=10055 E. 找出第 5大的元素是 $O (n)$ 量级，后序找出大于的元素也需要 $O (n)$

有向图的 DFS 不仅在起点任意，⽽且每⼀步迭代往往都会有多个顶点可供选择，故所⽣成的 DFS 森林并不唯⼀确定，且其中所含（ A, B, D ）的数量也可能不同。 A）树边 B）前向边 C）后向边 D）跨越边 E）以上皆⾮

A. 如果不是从零入度点开始 DFS，那么无法完成强连通分量的遍历，因此 TREE 边是可以不同的。 B. CROSS 和 FORWARD 边都是可以通过调整路径的选择而避免的。 C. BACKWARD 边出现说明存在环路，而构成环路的边中任何一条边都可以作为 BACKWARD，因此 BACKWARD 的数量是不会变的。

相对于除余法，MAD 法在（ B, C ）⽅⾯有所改进。 A）计算速度 B）⾼阶均匀性 C）不动点 D）满射性 E）以上皆⾮

PPT

将硬币换成理想的骰⼦，且约定投出“6”时新塔才停⽌⽣⻓。于是对于同样存放 n 个元素的跳转表⽽⾔，（ A, C, D ）的期望值将有所增⻓，但仍保持 O(1）。 A）查找过程中，在同⼀⾼度连续跳转的次数 B）查找过程中，由“向右”到“向下”转折的次数 C）查找过程中，沿同⼀座塔连续下⾏的层数 D）（在查找定位之后）为创建⼀座新塔所需的时间

A. 同一高度横向跳转的期望为几何分布的期望 O(1) B. 纵向跳转的次数累计不超过 expected-O(logn) C. 沿同一座塔下行的层数取决于塔的高度，此高度的期望为几何分布的期望 1/p = 6 D. 建造新塔的高度的期望为 6

（ B, E, F ）属于针对闭散列策略的冲突排解⽅法。 A）multiple slots B）linear probing C）overflow area D）separate chaining E）quadratic probing F）double hashing

开放散列：A, C, D 封闭散列：B, E, F

对于任何⼀颗⼆叉树 T，其右、左⼦树的规模之⽐ λ=T.re().size () / T.le().size () 称作右偏率。对于（常规）⾼度同为 h 的 AVL 树（A），红⿊树（R），左式堆（L），若分别考察其λ所能达到的最⼤值，则在 h ⾜够⼤之后，三者按此指标的排列次序应是（ C D ）。 A）L < R < A B）L < A < R C）R < A < L D）A < R < L E）以上皆非

Fib-AVL 可以达到 AVL 的最大右偏率：对于高度为 h 的 Fib-AVL 树，其总节点数为 fib (h+3)-1，则左子树或右子树递归地也是 Fib-AVL 树，并且分别节点数为 fib (h+1)-1和 fib (h+2)-1，因此最大右偏率的比值为 $λ = h \to \infty lim \frac{ϕ ^{h + 2} - 1}{ϕ ^{h + 1} - 1} = ϕ \approx 1.618$ Red-black 树如果从(2,4)-Tree 的角度来看，不妨设根节点只有一个关键码，其右子树中所有节点的关键码为 3，左子树中关键码为 1，因此右子树的规模为 $N_{R} = 3^{h - 1} - 1$ ，左子树的规模为 $N_{L} = 2^{h - 1} - 1$ ，因此最大右偏率的比值为 $λ = h \to \infty lim \frac{3 ^{h - 1} - 1}{2 ^{h - 1} - 1} = \frac{3 ^{h}}{2 ^{h}} \times \frac{2}{3} = + \infty$ 。左式堆对右子树的高度没有任何限制，λ可以达到无穷大，但显然该无穷大比红黑树的无穷大更高阶。综上，以指标递增排序为：A < R < L

以下数据结构中，空间复杂度不超过线性的有（ A, B, D, F ）。 A）2d-tree B）3d-tree C）2D range tree D）interval tree E）segment tree F）priority search tree

kdtree: $O (n)$ range tree: $O (n lo g^{d - 1} n)$ interval tree: $O (n)$ segment tree: $O (n lo g n)$ priority search tree: $O (n)$

KMP

给出以下模式串的 next[] 表和改进版 next[] 表

Index:       0   1   2   3   4   5   6   7   8   9   10  11  12
P[]:         知  之  为  知  之  不  知  为  不  知  是  知  也
next[]:     -1   0   0   0   1   2   0   1   0   0   1   0   1
imp-next[]: -1   0   0  -1   0   2  -1   1   0  -1   1  -1   1

快速划分

rank:    0   1   2   3   4   5   6   7   8   9   10  11  12  13  14
A[0,15): 20 17A 16A  11 16B 28A  27 17B  48 28B  33  14  22  24  23

template <typename T> //通过调整元素位置，构造出区间[lo, hi)内的一个轴点
Rank Vector<T>::partition( Rank lo, Rank hi ) { // LUG版：基本形式
   swap( _elem[lo], _elem[lo + rand() % ( hi - lo )] ); //任选一个元素与首元素交换
   T pivot = _elem[lo]; //经以上交换，等效于随机选取候选轴点
   while ( lo < hi ) { //从两端交替扫描，直至相遇
      do hi--; while ( ( lo < hi ) && ( pivot <= _elem[hi] ) ); //向左拓展后缀G
      if ( lo < hi ) _elem[lo] = _elem[hi]; //阻挡者归入前缀L，即凡小于轴点者，归入L部分
      do lo++; while ( ( lo < hi ) && ( _elem[lo] <= pivot ) ); //向右拓展前缀L
      if ( lo < hi ) _elem[hi] = _elem[lo]; //阻挡者归入后缀G，即凡大于轴点者，归入G
   } // assert: quit with lo == hi or hi + 1
   _elem[hi] = pivot; //候选轴点置于前缀、后缀之间，它便名副其实
   return hi; //返回轴点的秩
}

指向原始笔记的链接

假定算法首句中 rand()的返回值为 12 ，试给出一趟快速划分的过程及结果。

rank:    0   1   2   3   4   5   6   7   8   9   10  11  12  13  14
A[0,15): 20 17A 16A  11 16B 28A  27 17B  48 28B  33  14  22  24  23 
0        22 .............................................20 .......
1        (22) ...................................................23
2        (22) ...............................................24  23
3        20 ............................................(20) 24  23
4        20 17A ........................................(20) 24  23
5        20 17A 16A ....................................(20) 24  23
6        20 17A 16A  11 ................................(20) 24  23
7        20 17A 16A  11 16B ............................(20) 24  23
8        20 17A 16A  11 16B (28A) ...................... 28A 24  23
9        20 17A 16A  11 16B  14 ....................(14) 28A 24  23
10       20 17A 16A  11 16B  14 (27).................27  28A 24  23
11       20 17A 16A  11 16B  14 (27).............33  27  28A 24  23
12       20 17A 16A  11 16B  14 (27) ........28B 33  27  28A 24  23
13       20 17A 16A  11 16B  14 (27) .....48 28B 33  27  28A 24  23
14       20 17A 16A  11 16B  14 17B (17B) 48 28B 33  27  28A 24  23
15       20 17A 16A  11 16B  14 17B  22   48 28B 33  27  28A 24  23

Heapsort 过程

对以下整型向量做就地堆排序，试给出（采用R. Floyd 算法）建堆以及此后各步迭代中向量的内容。

A[0,15):    50  63  8  25  54A  45  36  91  83A  88  83B  15  54B  58  13
heapify():
            ......................  58  .........................  36  13
		    ..................  54B 58  ................. 15  45   36  13
			............... 88  54B 58  ........ 54A 83B  15  45   36  13
			.......... 91   88  54B 58  25  83A  54A 83B  15  45   36  13
递归地下滤  ........58 91   88  54B 36  25  83A  54A 83B  15  45    8  13
			....91  58 83A  88  54B 36  25  63   54A 83B  15  45    8  13
			91  88  58 83A  83B 54B 36  25  63   54A  50  15  45    8  13

rank():
			0
			    1   2
					    3    4   5   6
									     7   8    9   10   11  12   13  14

heapsort():
			88  83A ..  63  ............... 13 ........................ 91
			83A 83B ..  63  54A ........... 13    8 ............... 88  91
			83B 63  ..  45  54A ........... 13    8 .......... 83A  88  91
			63  54A ..  45   50 ....... 25  13    8   15  83B  83A  88  91
			58  54A 54B 45   50  15 36  25  13    8   63  83B  83A  88  91
			54A 50  54B 45    8  15 36  25  13   58   63  83B  83A  88  91
			54B 50  36  45    8  15 13  25  54A  58   63  83B  83A  88  91
			50  45  36  25    8  15 13 54B  54A  58   63  83B  83A  88  91
			45  25  36  13    8  15 50 54B  54A  58   63  83B  83A  88  91
			36  25  15  13    8  45 50 54B  54A  58   63  83B  83A  88  91
			25  13  15   8   36  45 50 54B  54A  58   63  83B  83A  88  91
			15  13   8  25   36  45 50 54B  54A  58   63  83B  83A  88  91
			13   8  15  25   36  45 50 54B  54A  58   63  83B  83A  88  91
			8   13  15  25   36  45 50 54B  54A  58   63  83B  83A  88  91

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索

2014-final

判断

选择

KMP

快速划分

Heapsort 过程

关系图谱

目录

反向链接