🌰Senjl's Digital Garden🐉

Recent writing

2010-mid

8分钟阅读

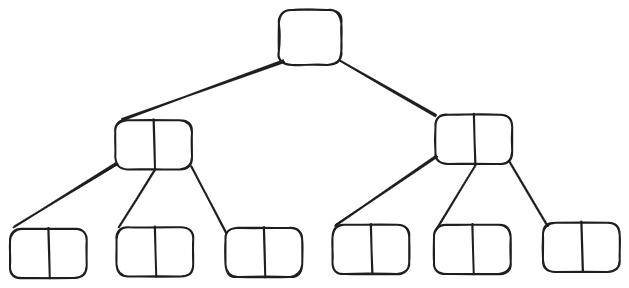
判断

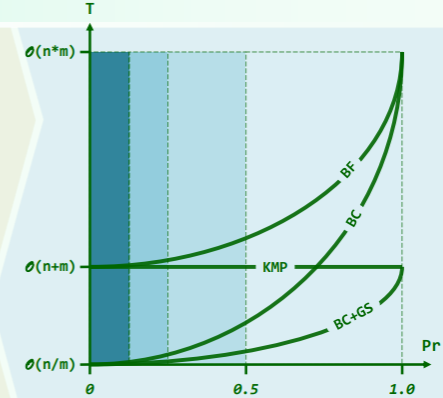
  1. 在对二进制串做匹配时，采用 next[] 表比采用 BC[] 表通常效率更高。

✅ 正确答案：❌ 二进制串通常是随机的，Pr=0.5，此时 KMP 的效率反而更低。

  1. 所有叶节点深度一致的有根二叉树，必为满树。

❌ 叶节点的父亲的度数为 1，也可以满足深度一致的要求，但并不是满树

  1. 完全二叉树的子树，也一定是完全二叉树。

✅

  1. 由合法的先序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。

✅

  1. 在 Huffman 算法过程中，权重小的内部节点必然早于权重大的内部节点被创建。

✅

  1. 由同一组互异关键码，按不同次序逐个插入而生成的 BST 必互异。

❌ 231 和 213

  1. BST 中新插入的节点，必是叶节点。

✅

  1. 在 AVL 树中删除节点之后若树高降低，则必然做过旋转调整。

✅ 正确答案：❌ 删除未导致失衡，也可能降低树高——即删除的节点在最底层，且该层只有一个节点。

多重选择

  1. 在（  C   ）中，越深的节点必然越多。 A. 二叉树 B. AVL 树 C. 满二叉树 D. 完全二叉树 E. 以上皆非

A 太宽泛，只要能举出反例就能否决 B Fib-AVL 树最深层只有一个节点 D 完全二叉树最深层可能只有极少的叶节点

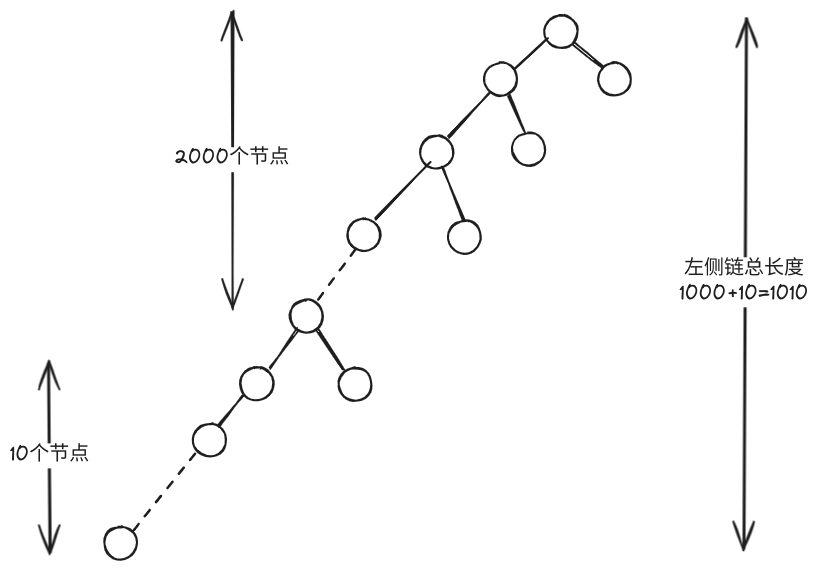
  1. 在包含 2010 个节点的 AVL 树中，最高与最低叶节点之间的深度差最大可达（  E   ）。 A. 8 B. 9 C. 10 D. 11 E. 以上皆非

含有 n 个节点的 AVL 树与其高度 h 的关系是： ，而 fib (17)=1597, fib (18)=2584，所以 n=2010 时，h 为 17-3=14 而最高叶节点的深度不小于 h/2，最低叶节点的深度为 h，因此深度差应为 7.

  1. 由 6 个节点组成的二叉树，若中序遍历序列为 ABCDEF，则不可能的后序遍历序列是（ A, D ）。 A. CBEADF B. ADFECB C. ABDECF D. BDACFE E. 以上皆非

后序遍历序列中最后一位一定是根节点，而根节点想做中序遍历序列的最后一位，一定是根节点只有左子树的情况 思路就是尝试组成一棵二叉树，出现悖论的就可选中： A 无法构成二叉树 B 可以构成： C 可以构成： D 无法构成

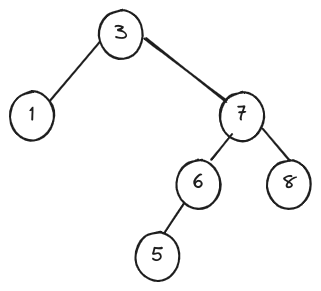
  1. 下图有可能是一棵刚做过 BST 的（ A, D ）操作，但尚未旋转调整的 AVL 树。 A. delete(2) B. insert(3) C. detele(4) D. insert(5) E. insert(8)

  1. 设 x 为某伸展树中的最大关键码，则在 find (x)过程中不可能实施（ A, B, C ）调整。 A. zig‐zig B. zig‐zag C. zag‐zig D. zag‐zag E. 以上皆非

伸展树最大关键码一定在沿着右侧链不变方向、直行到的最深处，因此此时抬升节点只能 zagzag，其余涉及到 zig 的动作，都不符合调整的拓扑要求。

填空

  1. 由 2010 个节点组成的完全二叉树，共有（  1005  ）个叶节点。

2^10 - 1 = 1023 2^11 - 1 = 2047 第 11 层节点数：2^10=1024 (最多)，现在有 2010-1023=987个 第 10 层节点数：2^9=512，因此第 10 层有叶子的节点数为 ，因此第 10 层的叶节点有 512-494=18个 因此总叶节点数=18+987=1005个

  1. 由 5 个互异节点组成、先序遍历序列与层次遍历序列相同的 BST，共有（  29  ）棵。

  1. 在由 2010 个节点组成的二叉树中，若单分支节点不超过 10 个，则对其做迭代式中序遍历时辅助栈的容量为（   1005 1010    ）即足够。

中序遍历辅助栈中元素数，即为当前节点在左链中的祖先数+当前节点右子树的左链长度。 而要使二叉树高度最大，形态应当如下：

  1. 由 2010 节点组成的 AVL 树，最大高度可达（   14    ）。

含有 n 个节点的 AVL 树与其高度 h 的关系是：

  1. 在节点数为 2010 的 AVL 树中删除一节点，至多可能造成（   1   ）个节点失衡，至多需做（  14  ）次旋转调整。

Fib-AVL 树的高度是节点数一定时，AVL 可以达到的最大高度。

  1. 高度为 3 的 5 阶 B‐树，至多可存放（  124 ）个关键码，至少需存放（  17   ）个。

计算

  1. 计算以下模式串的 next、改进 next、BC表
j:           0   1   2   3   4   5   6
P[j]:        B   A   R   B   A   R   A
next[]:     -1   0   0   0   1   2   3
imp-next[]: -1   0   0  -1   0   0   3
BC[]:        3   6   5   3   6   5   6

j:           0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
P[j]:        T  A  R  S  O  M  E  _  T  A  T  A  R  S  U  S
next[]:     -1  0  0  0  0  0  0  0  0  1  2  1  2  3  4  0
imp-next[]: -1  0  0  0  0  0  0  0 -1  0  2  0  0  0  4  0
BC[]:       10 11 12 15  4  5  6  7 10 11 10 11 12 15 14 15

这里 BC 表是错的，请阅读代码后重新填写（提示：注意 BC 表初始化时的值）

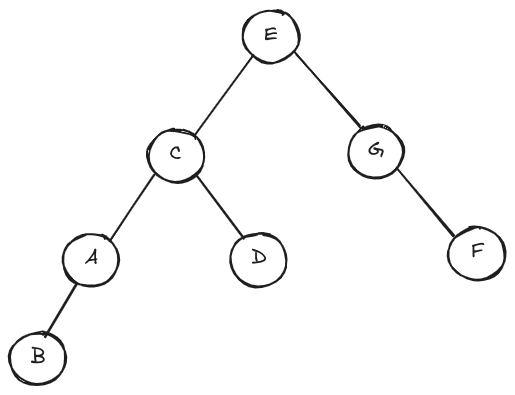
  1. 补全二叉树先序、后序遍历的序列
Preorder:  E   C   _   B   D   _   F
Postorder: B   A   _   _   _   G   _

preorder: E C A B D G F postorder: B A D C F G E 一种可能的二叉树拓扑图：

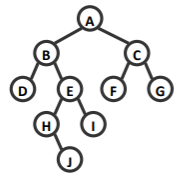
  1. 按如下算法遍历二叉树 T，试给出每次执行 PrintStack(S)的输出结果 
StatusTraversal(Bintree T, Status (*Visit)(TElemType e)) {
	Stack* S = StackInit(‐1);
	while (true) {
		GoAlongLeftBranch(S, T);  
		if (StackEmpty(S)) break;     
		PrintStack(S);//输出栈S中的内容     
		T = (Bintree) Pop(S); 
		Visit(T‐>data); 
		T = RChild(T); 
	} 
	StackDestroy(S); 
	return OK; 
}

栈底 ⇐------PrintStack ()输出的内容-------⇒ 栈顶

  1. A B D
  2. A B
  3. A E H
  4. A E J
  5. A E
  6. A I
  7. A
  8. C F
  9. C
  10. G
  11. 不会到达这一步，在之前就会 break

本质上是一个中序遍历的迭代版本。

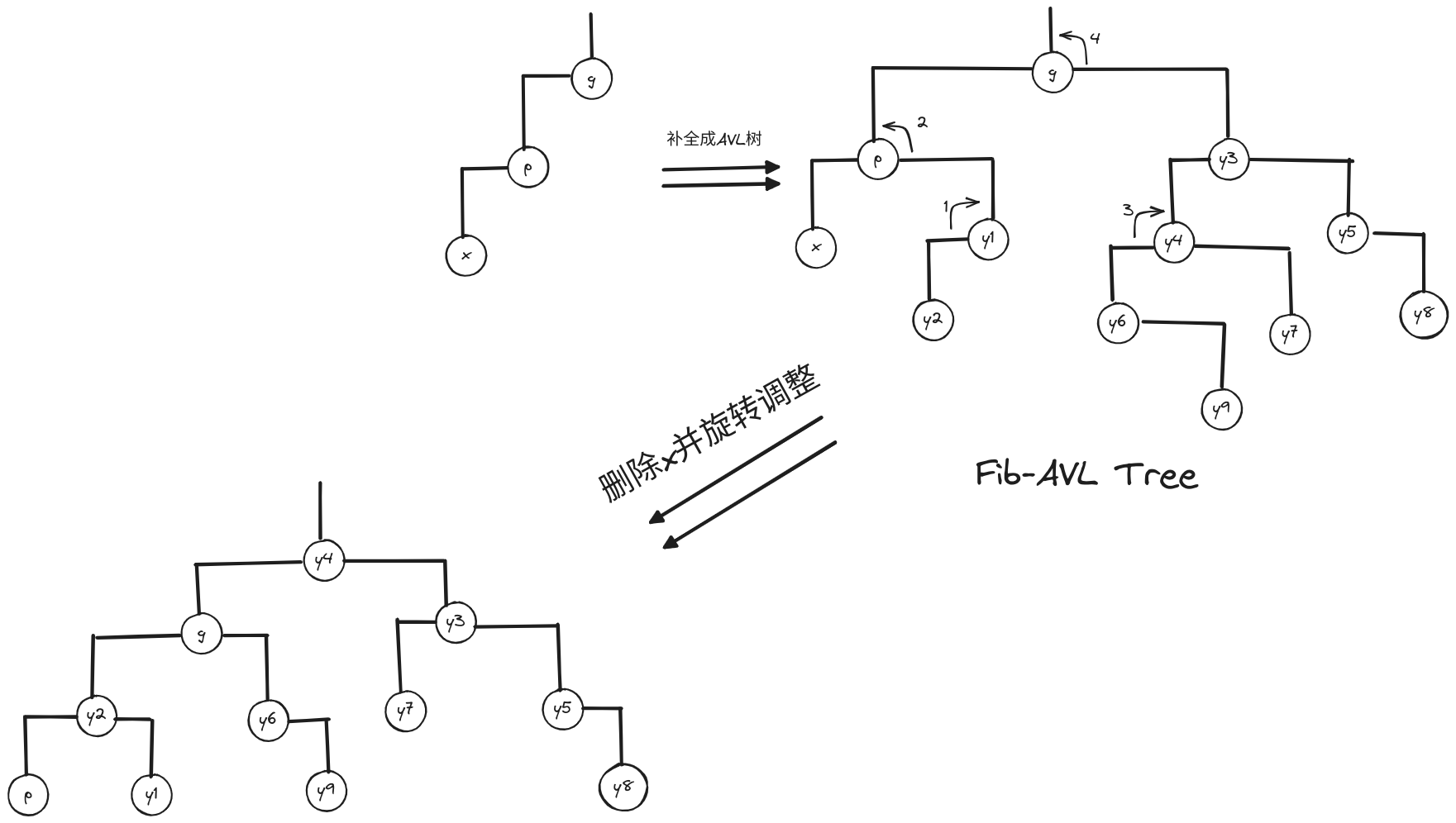
  1. 节点 x 的父节点和祖父节点分别记作 p 和 g。试在下图中补充尽可能少的节点以构造一棵 AVL 树，使得：
    1. 在摘除 x 之后，p 失衡；
    2. 经局部双旋调整之后，g 因失衡需再次实施双旋调整。
    3. 请同时在右侧画出最终恢复平衡的树形。

关系图谱