串的相关术语

- 子串:
- 前缀:
- 后缀:
三者关系:
ADT

本章的重点在串的模式匹配算法。
模式匹配问题
模式匹配:从一段文本(称为 text)中,查找是否存在想要的内容(称为模式 pattern),若存在则返回位置或其它信息。(暗含着,模式串是与文本串相关联甚至就是其中子串的可能)
其中,文本串的长度 |T|=n,模式串的长度 |P|=m,他们之间存在这样的关系:2 << m << n。
并且,它们的字符集Σ,其中字符种类有 s = |Σ| 个,因此匹配的概率:
蛮力策略
思路与复杂度

- 逐位查看是否匹配,若不匹配,则后移一位继续查找;
- 最好情况:不匹配的情况仅发生在第一位,因此模式串能够快速滑动越果失配之处——到达匹配处或文本串末尾——时间复杂度Ω(n)
- 最坏情况:每一次查看都是匹配,但直到模式串 P 的末尾才失配——每轮查看都反复地逐位比较模式串的每一位——时间复杂度
O(n*m)- 比如:模式串 P 为 0001,而文本串为 00000000…
实现:版本 1
/************************************************
* Text : 0 1 2 . . . i-j . . . i . . . . . n-1
* ------------|---------|------------
* Pattern: 0 . . . . j . .
* |---------|
************************************************/
int match ( char* P, char* T ) { //串匹配算法(Brute-force-1)
size_t n = strlen ( T ), i = 0; //文本串长度、当前接受比对字符的位置
size_t m = strlen ( P ), j = 0; //模式串长度、当前接受比对字符的位置
while ( j < m && i < n ) //自左向右逐个比对字符
if ( T[i] == P[j] ) //若匹配
{ i ++; j ++; } //则转到下一对字符
else //否则
{ i -= j - 1; j = 0; }//T串回退、P复位
return i - j; //最终的对齐位置:藉此足以判断匹配结果
}
实现:版本 2
/************************************************
* Text : 0 1 2 . . . i i+1 . . . i+j . . n-1
* ------------|-----------|------------
* Pattern : 0 1 . . j . .
* |-----------|
*************************************************/
int match ( char* P, char* T ) { //串匹配算法(Brute-force-2)
size_t n = strlen ( T ), i = 0; //文本串长度、与模式串首字符的对齐位置
size_t m = strlen ( P ), j; //模式串长度、当前接受比对字符的位置
for ( i = 0; i < n - m + 1; i++ ) { //文本串从第i个字符起,与
for ( j = 0; j < m; j++ ) //模式串中对应的字符逐个比对
if ( T[i + j] != P[j] ) break; //若失配,模式串整体右移一个字符,再做一轮比对
}
if ( j >= m ) break; //找到匹配子串
}
return i; //最终的对齐位置:藉此足以判断匹配结果
}
两个版本是等价的。
KMP 法
思路
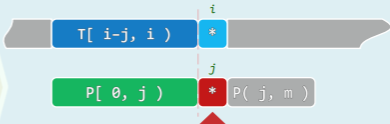
- 在任一时刻,都有
T[ i-j, i ) == P[ 0, j ) - 亦即,我们业已掌握
T[i-j,i)的所有信息,既如此,一旦失配,就应已知哪些位置值得/不必对齐,而且在下一轮比对中T[i−j',i)可径直接受,而不必再做比对: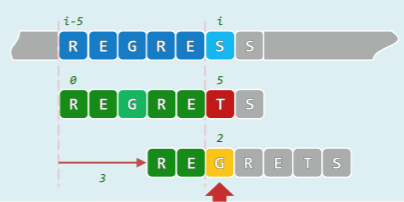 如此,i 将永远不必回退!(BF 算法的低效之处,正在于此 —— 一旦失配就要回退)
如此,i 将永远不必回退!(BF 算法的低效之处,正在于此 —— 一旦失配就要回退) - 比对成功,则与 j 同步前进一个字符
- 否则,j 更新为某更小的 t,并继续比对
- 如此优化,可以使得 P 快速右移,并且避免重复比对已确定的子串
- 那么,为确定移动的 t,需花费多少时间和空间?更重要地,可否在事先就确定?——构造
next[]表。
next[] 查询表
要移动的距离 t,不仅可以事先确定,而且仅根据 P[0,j) = T[i-j,i) 即可确定:

- 视失败的位置 j,无非 m 种情况 (即是模式串的长度)
- 构造查询表
next[0,m),做好预案 - 一旦在
P[j]处失配,只需将 j 替换为next[j],继续与T[i]比对即可。 - 换言之,
next[j]就是模式串P[0, j-1)子串的公共真前缀、真后缀的最大匹配长度。
next[] 表实例
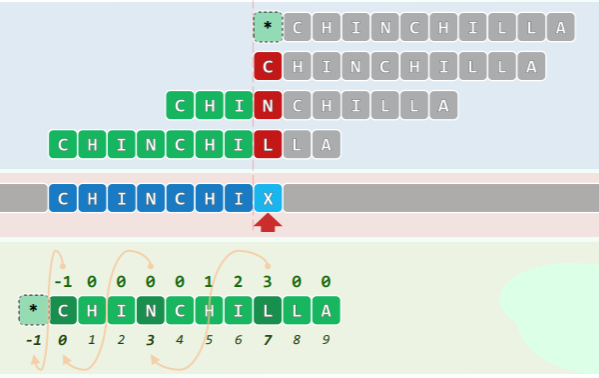
[! example] 另举一例: 构造 next 表:
[index]: 0 1 2 3 4 5 6 7 8 9 10 11Pattern: A B C A A B B A B C A Bnext[j]:-1 0 0 0 1 1 2 0 1 2 3 4
KMP 算法的实现
int match ( char* P, char* T ) { //KMP算法
int* next = buildNext ( P ); //构造next表
int n = ( int ) strlen ( T ), i = 0; //文本串指针
int m = ( int ) strlen ( P ), j = 0; //模式串指针
while ( j < m && i < n ) { //自左向右逐个比对字符
if ( 0 > j || T[i] == P[j] ) //若匹配,或P已移出最左侧(两个判断的次序不可交换)
{ i ++; j ++; } //则转到下一字符
else //否则
j = next[j]; //模式串右移(注意:文本串不用回退)
delete [] next; //释放next表
return i - j;
}
int* buildNext ( char* P ) { //构造模式串P的next表
size_t m = strlen ( P ), j = 0; //“主”串指针
int* next = new int[m]; int t = next[0] = -1; //next表,首项必为-1
while ( j < m - 1 )
if ( 0 > t || P[t] == P[j] ) { //匹配
++t; ++j; next[j] = t; //则递增赋值:此处可改进...
} else //否则
t = next[t]; //继续尝试下一值得尝试的位置
return next;
}
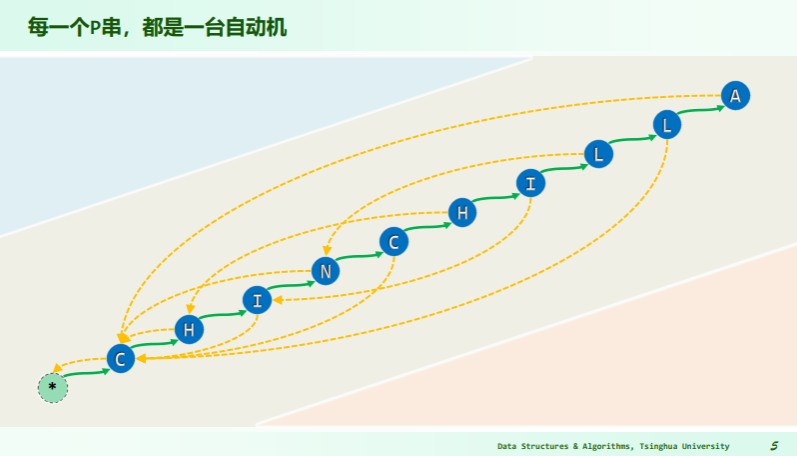
理解 next[] 表

- 所有自匹配的长度:
- 因总包含 0 而非空:
- 故可以取最大长度:位移最小,不致回溯:
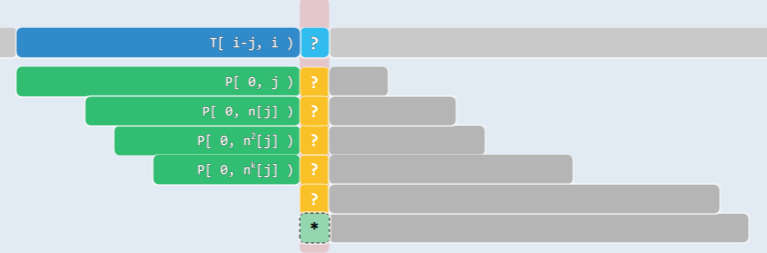
- 记:
- 同一文本串中元素
T[i]可能依次与模式串 P 中的多个字符比对,其秩是:
构造 next[] 表
 模式串 P 在 j+1 处的自匹配,只比在 j 处的自匹配多出一个字符,即::
模式串 P 在 j+1 处的自匹配,只比在 j 处的自匹配多出一个字符,即::
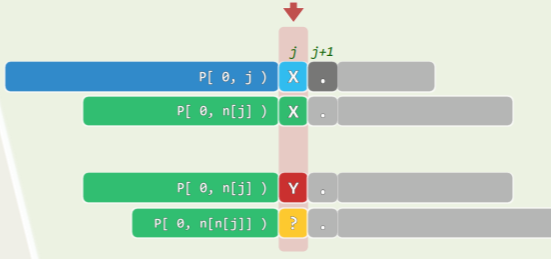
int* buildNext ( char* P ) { //构造模式串P的next表
size_t m = strlen ( P ), j = 0; //“主”串指针
int* next = new int[m]; int t = next[0] = -1; //next表,首项必为-1
while ( j < m - 1 )
if ( 0 > t || P[t] == P[j] ) { //匹配
++t; ++j; next[j] = t; //则递增赋值:此处可改进...
} else //否则
t = next[t]; //继续尝试下一值得尝试的位置
return next;
}
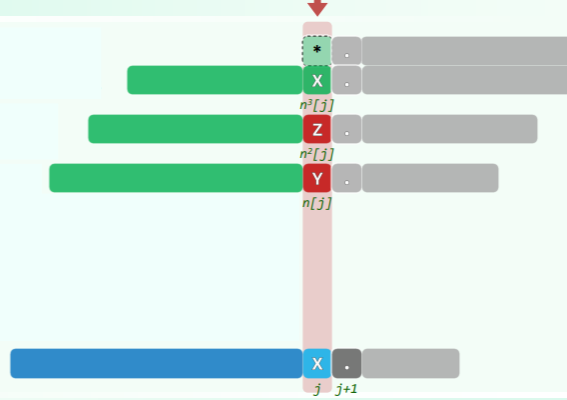




分摊分析
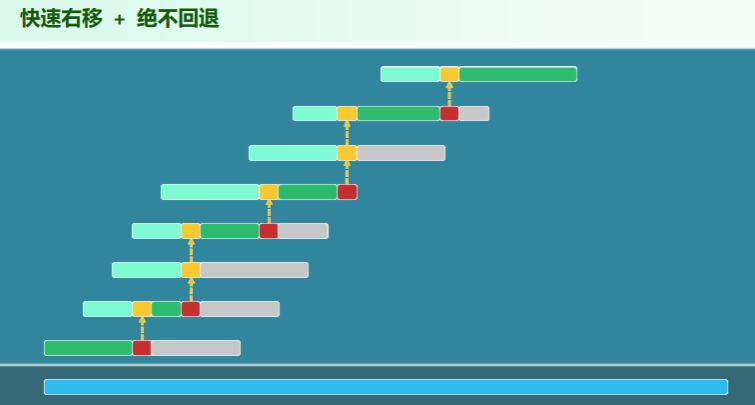
- 每个
T[i](红),都可能参与 Ω(m)次比对(黄) - 倘若共有 Ω(n) 个这样的
T[i]… 难道要达到Ω(n*m)吗? - 然而更细致的分析将表明 即便在最坏情况下,累计也不过 次
- 同理,构造
next[]也只需 O (m)
令:`k = 2*i - j` //欠精准,但还算够用的计步器
while ( j < m && i < n ) //k必随迭代而单调递增,故也是迭代步数的上界
if ( 0 > j || T[i] == P[j] )
{ i ++; j ++; } //k 恰好加1
else j = next[j]; //k 至少加1
初始:k = 0
算法结束时:k = 2*i - j <= 2(n - 1) - (-1) = 2n - 1
因此总体复杂度:构造 next[] O (m) + 查询 O (n) = O (m+n)
改进 next[]
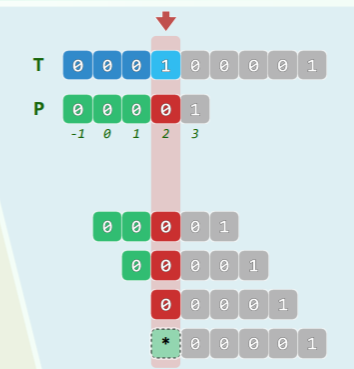
- 上图是一个反例:
- 先在
T[3]处比较失败 - 又:与
P[3]比对,失败 - 双:与
P[2] = P[next[3]]比对,失败 - 叒:与
P[1] = P[next[2]]比对,失败 - 叕:与
P[0] = P[next[1]]比对,失败
- 先在
- 最终,才前进到
T[4] - 事实上,后三次比较本来就可以避免,没有必要一错再错:
int* buildNext ( char* P ) { //构造模式串P的next表(改进版本)
size_t m = strlen ( P ), j = 0; //“主”串指针
int* next = new int[m]; int t = next[0] = -1; //next表,首项必为-1
while ( j < m - 1 )
if ( 0 > t || P[t] == P[j] ) { //匹配
if ( P[++t] != P[++j] ) //附加条件判断
next[j] = t; //唯当新的一对字符也匹配时,方照原方法赋值
else
next[j] = next[t]; //否则,改用next[t](此时必有:P[next[t]] != P[t] == P[j])
} else //失配
t = next[t]; //继续尝试下一值得尝试的位置
return next;
}
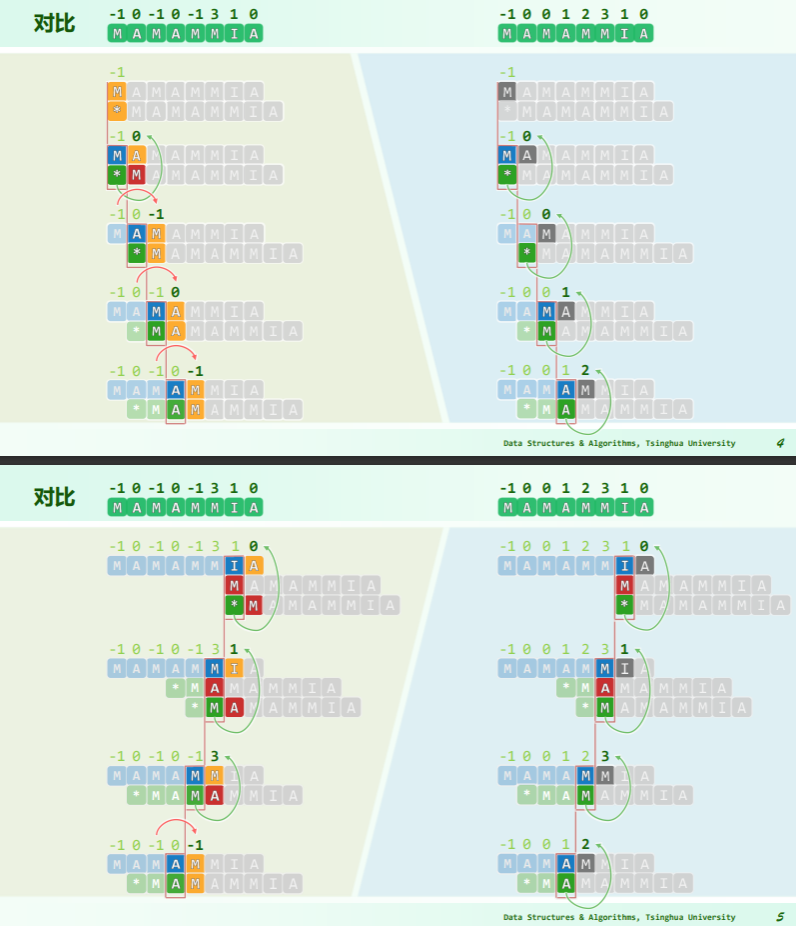
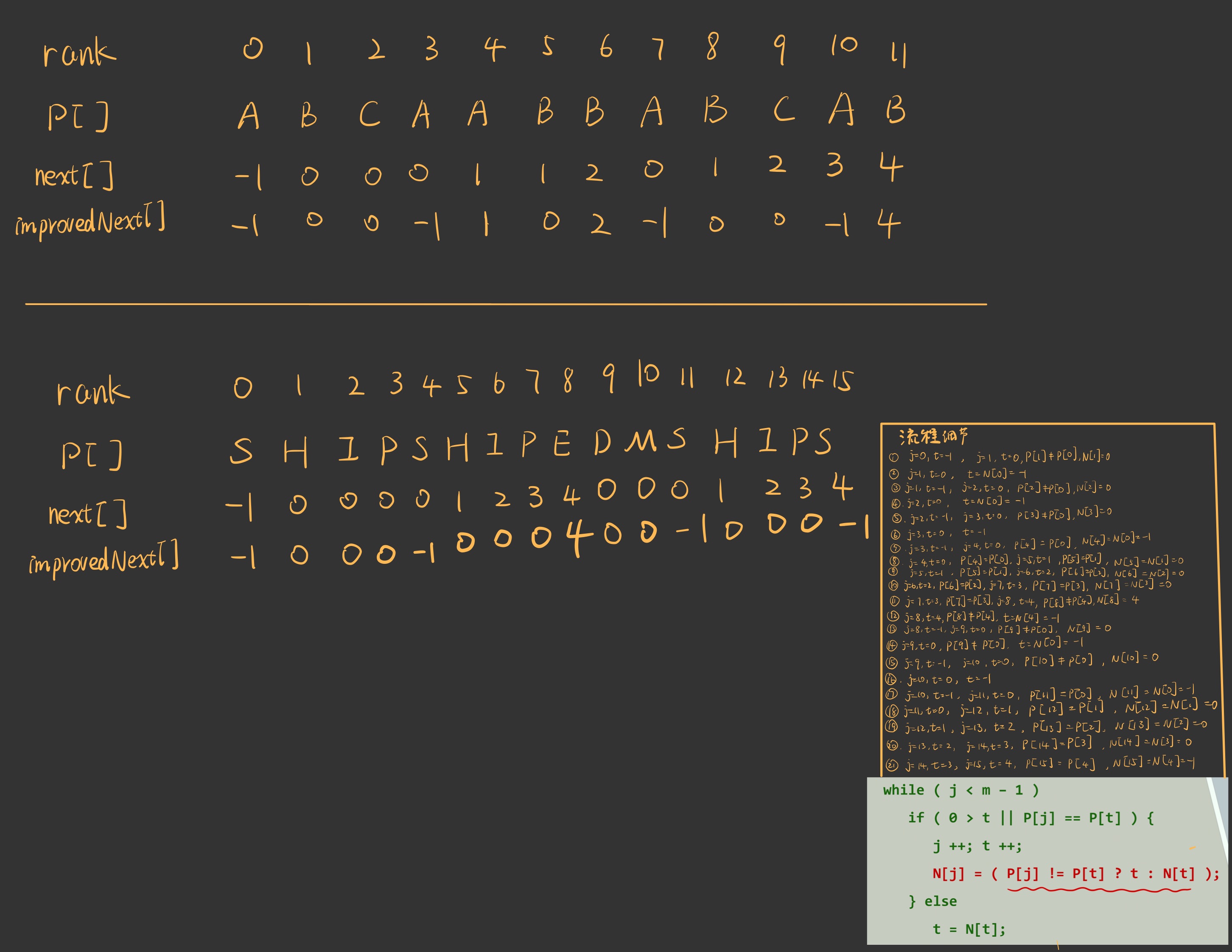
[! note] 通俗地描述 如果 j 和 next(j)这一项的字符一样,就可以把这一项的字符更新为 next(j)的 next 表项,直到从左到右刚好能保证每个的 next(j)都是最深那一层的 next
比如这个 p(5),他的 next 值为 0,而 p(0)=p(5),就可以把 next(5)更新为 next(0)
原版 next 是在查询 T 串的时候一层层 next,而改进版 next 就是在 P 串上直接把所有可以进行完的 next 操作完,就不用查询的时候再一层层找 next 了
适用范围
- 特别适用于顺序存储介质
- 单次匹配概率越大(字符集越小),优势越明显 //比如二进制串
- 否则,与蛮力算法的性能相差无几…
BM 法
每一趟比对都从末字符开始,自后向前,自右向左。
- 预处理: 根据模式串 P,预先构造
gs[]表和bc[]表 - 迭代:自右向左依次比对字符,找到极大的匹配后缀
- 若完全匹配,则返回位置;
- 否则查表确定 P 右移的适当位置,并重新自右向左比对
BC 策略
坏字符移动的思路
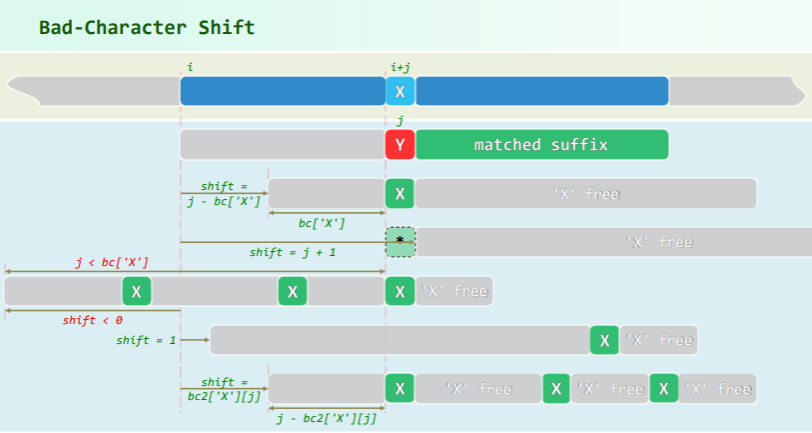
bc['X']指的是字符'X'在模式串 P 中的秩,若有多个字符,则返回最右边的'X'的秩。- 上图中文本串在秩
i+j处为字符'X',而模式串在秩j处为字符'Y',发生了失配,这里一共有两种情况:- 失配之前没有出现过字符
'X',则移动距离shift=j-bc['X'],其含义就是移动到失配左边的首个字符'X'处;极端情况是整个模式串都没有字符'X',那么就移动到模式串开始处; - 失配之前出现过字符
'X',则匹配串反而可能前移,移动到第一个'X'出现的位置,shift<0(注意移动距离的计算公式没变,仍是shift=j-bc['X'],但是失配位置的秩j< 字符'X'第一次出现的位置bc['X'])
- 失配之前没有出现过字符
如何解决模式串中多个字符 'X' 的问题?是否真的逐一尝试?
- 既不现实——无法保证永不后退,也不必要——左移隐含地表示左侧所有字符被否定排除了;
- 因此只需要向右移动 1 字符,重新开始配对即可。
可以看到 PPT 最后一行还给出二维 bc 表的使用方式,但这一策略其实并无必要—— [[A1-String-Exercise#11-5 二维bc[][] 表|习题 11-5 二维 bc 表分析]]
构建 bc[] 表
/************************************************
* 0 bc['X'] m-1
* | | |
* ...............X**********************
* .|<----- 'X' free ---->|
***********************************************/
int* buildBC( char* P ) { //构造Bad Character Shift表:O(m + 256)
int* bc = new int[256]; // BC表,与字符表ASCII等长
for ( size_t j = 0; j < 256; j++ ) bc[j] = -1; //初始化:首先假设所有字符均未在P中出现
for ( size_t m = strlen( P ), j = 0; j < m; j++ ) //自左向右扫描模式串P
bc[P[j]] = j; //将字符P[j]的BC项更新为j(单调递增)――画家算法
return bc;
}
以字符串 MAMMAMIA 为例:
Index: 0 1 2 3 4 5 6 7
Pattern: M A M M A M I A
bc[]: 5 7 5 5 7 5 6 7
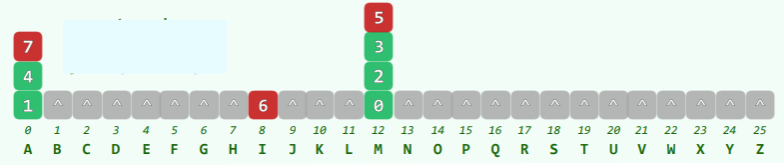
应用 bc[] 策略的 BM 算法
int match ( char* P, char* T ) { //Boyer-Morre算法(简化版,只考虑Bad Character Shift)
int* bc = buildBC ( P ); //预处理
size_t n = strlen ( T ), i = 0; //文本串长度、与模式串首字符的对齐位置
size_t m = strlen ( P ); //模式串长度
while ( n >= i + m ) { //在到达最右端前,不断右移模式串(可能不止一个字符)
int j = m - 1; //从模式串最末尾的字符开始
while ( P[j] == T[i+j] ) //自右向左比对
if ( 0 > --j ) break; /*DSA*/showProgress ( T, P, i, j ); getchar();
if ( j < 0 ) //若极大匹配后缀 == 整个模式串,则说明已经完全匹配,故
break; //返回匹配位置
else //否则,根据BC表
i += max ( 1, j - bc[T[i+j]] ); //相应地移动模式串,使得T[i+j]与P[bc[T[i+j]]]对齐
}
delete [] bc; //销毁BC表
return i;
}
性能分析
-
最好情况:
- 即只要 P 串不含
T[i+j](失配处)的字符,就可以直接移动 m 个字符——单次比较即可排除 m 个对齐位置 - 如 T=xxxx1xxxx1xxxx1…,而 P=00000
- 单次匹配概率越小,性能优势越明显,如 ASCII、Unicode 字符集
- P 越长,移动的效果也越明显
- 即只要 P 串不含
-
最坏情况:
- 退化成蛮力算法——P 串中含有失配处的字符,且字符在 T 串中的秩大于在 P 串中的秩,此时每次配对只能后移一个字符
- 如:T=00000000…,而 P=10000
- 单次匹配概率越大的场合,性能越接近于蛮力算法,如小字母表、Bitmap、DNA 中
GS 策略
- 借助以上
bc[]表,仅仅利用了失配比对提供的信息(教训) - 可否仿照 KMP,同时利用起匹配比对提供的信息(经验)?
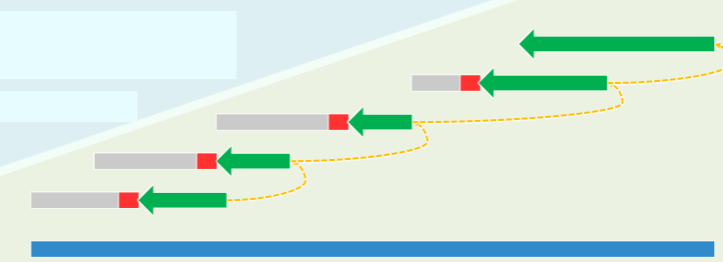
好后缀的经验
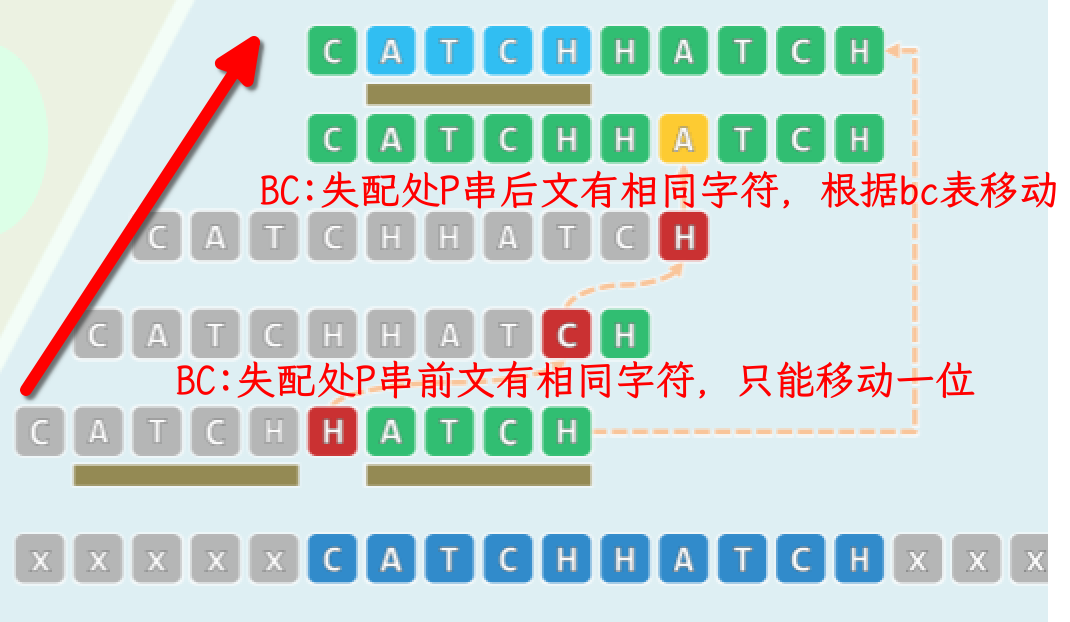
- 首趟比对虽失败,却积累了足够的经验(匹配的后缀 ATCH ,视为好后缀)
- 据此,可省去中间两趟,而直接转至最后一趟(P 右移 5 个字符)
- 这一规律与技巧与 KMP 如出一辙,只不过前后颠倒而已
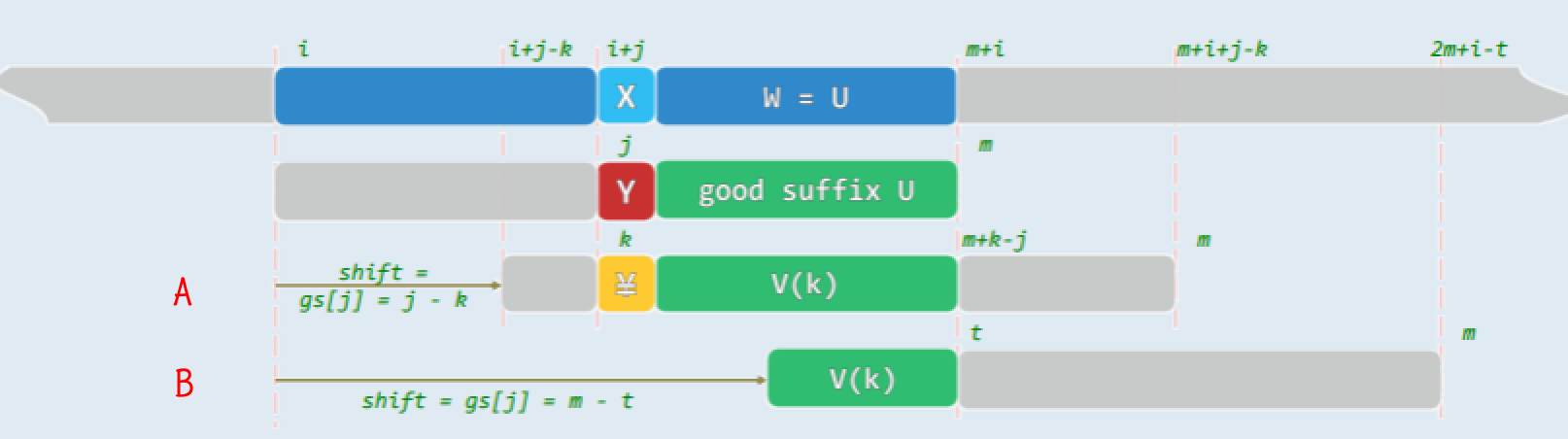
- 扫描比对失配于
T[i+j]='X'!='Y'=P[j]处,可以确定U=P(j,m)必然是好后缀 - 故下一次对齐必须使:
- U 重新与
V(k)=P(k, m+k-j)匹配,即汲取经验 P[k]=?!=Y=P[j],此处问号表示不能是 Y 的其它字符,即避免上一次的教训
- U 重新与
- 因此可以得到
gs[]表的构造思路:- 若 P 中的确存在这样的子串
V(k),则可选择其中 k 最大者(尽可能靠后),然后通过右移使之与 U 对齐(移动距离尽可能小),移动距离shift=gs[j]=j-k - 否则,在所有前缀
P[0,t)中,取与 U 的后缀匹配的最长者 ,移动距离shift=gs[j]=m-t//注意:有可能t=0
- 若 P 中的确存在这样的子串
- 无论如何,位移量仅取决于 j 和 P 本身——亦可预先计算,并制表待查
举例如下:
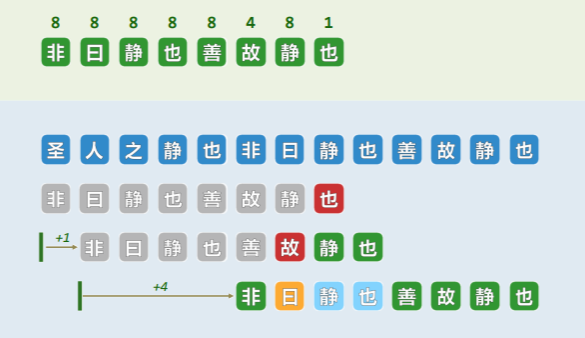
构造 gs[] 表-蛮力法
 根据定义,直接推导出
根据定义,直接推导出 gs[] 表:
- 对于每个好后缀
P(j, m),按照自后向前的次序,将其与 P 的每个子串P(k,m+k-j)逐个对齐, - 核对是否出现图示的两种匹配情况,一旦发现匹配,对应的位移量即是
gs[j]的取值
复杂度:
- 共 O (m)个后缀,
- 各需与 O (m)个子串对齐,
- 每次对齐后在最坏情况下都需要比对 O (m)次
- 因此最坏情况需要 的时间
构造 gs[] 表——借助最大匹配后缀串
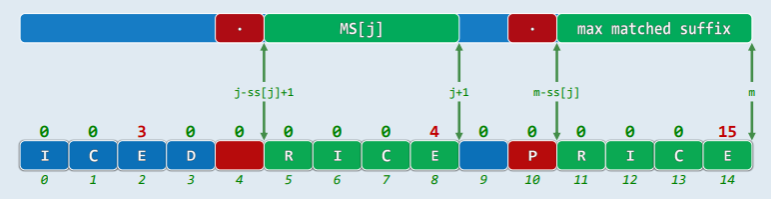 对于任一整数 ,在
对于任一整数 ,在 P[0,j] 的所有后缀中,考查那些与 P 的某一后缀匹配者:
- 若将其中的最长者记作
MS[j]——MS[j]=P[j-ss[j],j],则ss[j]就是该串的长度|MS[j]|。 - 因此
- 特别地,当
MS[j]不存在时,取ss[j]=0;当j=m-1时,必有 s=m,此时P(-1,m-1]=P[0,m)
// ss[]表示例
index: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
P[i]: I C E D '' R I C E '' P R I C E
ss[i]: 0 0 3 0 0 0 0 0 4 0 0 0 0 0 15
ss[] 表蕴含了 gs[] 表的所有信息,可以快速地根据 ss[] 表构造 gs[] 表:
-
若
ss[j]=j+1,则对于任何i<m-j-1,m-j-1必是gs[i]的一个候选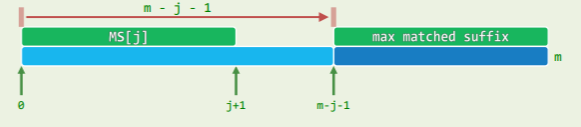
- 此时
MS[j]是就是整个前缀P[0,j](对应上面示例的index=2处), - 此时对于
P[m-j-1](上面示例的P[12])左侧的每个字符P[i]而言,就是下图的 B 情况,因此 m-j-1 都应该是gs[i]取值的一个候选 (对上面示例而言,gs[0..11]的候选有 12) 
-
若
ss[j]<=j,则m-j-1必是gs[m-ss[j]-1]的一个候选
- 此时
MS[j]只是P[0,j]的一个真后缀(上面示例的index=8处,实际上除了index=2和index=14处都满足这一条件,0 代表后缀为空,但是此时 0 对应的P[m-ss[j]-1]==P[m-1]即最后一项,对其他项无影响), - 此时对于字符
P[m-ss[j]-1](上面示例的P[15-ss[8]-1]=P[10]处)而言,对应于情况 A,同时还满足P[m-ss[j]-1]!=P[j-ss[j]]('P'=P[10]!=P[8-ss[8]]=P[4]=''当然也成立),则 m-j-1 也应是gs[m-ss[j]-1]取值的一个候选 (即15-8-1=6也是gs[10]的候选) - 对于字符
P[m-ss[0]-1]=P[14]='E'!=P[0-ss[0]]='I'处,则m-j-1=15-0-1=14也是gs[14]的候选。但是为了安全,最后一位只能填 1
因此,根据此前的定义,每个位置 i 所对应的 gs[i] 只可能来自于以上候选,进一步地,既然 gs[i] 最终取值是上述候选的最小者(最安全者),故仿照构造 bc[] 的画家算法,累计用时不超过 O(m)。
如何构造 ss[]?
- 蛮力法:对每个字符都扫描一遍,累计
O(m^2) - 自后向前逆向扫描,只需
O(m)时间:- 自后向前地逆向扫描,并逐一计算出各字符
P[j]对应的ss[j]值。 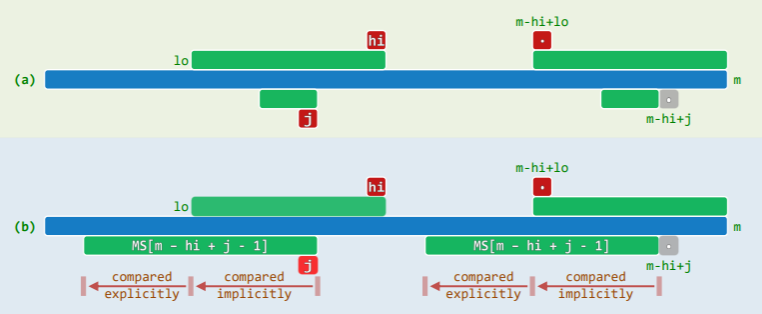
- 如图所示,因此时必有
P[j] = P[m - hi + j - 1],故可利用此前已计算出的ss[m - hi + j - 1],分两种情况快速地导出ss[j]。在此期间,只需动态地记录当前的极长匹配后缀:P(lo, hi] = P[m - hi + lo, m)- 第一种情况如图 (a)所示,设:
ss[m - hi + j - 1] <= j - lo此时,ss[m - hi + j - 1]也是ss[j]可能的最大取值,于是便可直接得到:ss[j] = ss[m - hi + j - 1] - 第二种情况如图 (b)所示,设:
j - lo < ss[m - hi + j - 1]此时,至少仍有:P(lo, j] = P[m - hi + lo, m - hi + j)故只需将P(j - ss[m - hi + j - 1], lo]与 P[m - hi + j - ss[m - hi + j - 1], m - hi + lo)做一比对,也可确定ss[j]。当然,这种情况下极大匹配串的边界 lo 和 hi 也需相应左移(递减)。
- 第一种情况如图 (a)所示,设:
- 同样地,以上构思只要实现得当,也只需
O(m)时间即可构造出ss[]表
- 自后向前地逆向扫描,并逐一计算出各字符
构造代码如下所示:
int* buildSS ( char* P ) { //构造最大匹配后缀长度表:O(m)
int m = strlen ( P ); int* ss = new int[m]; //Suffix Size表
ss[m - 1] = m; //对最后一个字符而言,与之匹配的最长后缀就是整个P串
// 以下,从倒数第二个字符起自右向左扫描P,依次计算出ss[]其余各项
for ( int lo = m - 1, hi = m - 1, j = lo - 1; j >= 0; j -- )
if ( ( lo < j ) && ( ss[m - hi + j - 1] < j - lo ) ) //情况一
ss[j] = ss[m - hi + j - 1]; //直接利用此前已计算出的ss[]
else { //情况二
hi = j; lo = min ( lo, hi );
while ( ( 0 <= lo ) && ( P[lo] == P[m - hi + lo - 1] ) ) //二重循环?
lo--; //逐个对比处于(lo, hi]前端的字符
ss[j] = hi - lo;
}
return ss;
}
int* buildGS ( char* P ) { //构造好后缀位移量表:O(m)
int* ss = buildSS ( P ); //Suffix Size table
size_t m = strlen ( P ); int* gs = new int[m]; //Good Suffix shift table
for ( size_t j = 0; j < m; j ++ ) gs[j] = m; //初始化
for ( size_t i = 0, j = m - 1; j < UINT_MAX; j-- ) //逆向逐一扫描各字符P[j]
if ( j + 1 == ss[j] ) //若P[0, j] = P[m - j - 1, m),则
while ( i < m - j - 1 ) //对于P[m - j - 1]左侧的每个字符P[i]而言(二重循环?)
gs[i++] = m - j - 1; //m - j - 1都是gs[i]的一种选择
for ( size_t j = 0; j < m - 1; j ++ ) //画家算法:正向扫描P[]各字符,gs[j]不断递减,直至最小
gs[m - ss[j] - 1] = m - j - 1; //m - j - 1必是其gs[m - ss[j] - 1]值的一种选择
delete [] ss; return gs;
}
性能分析
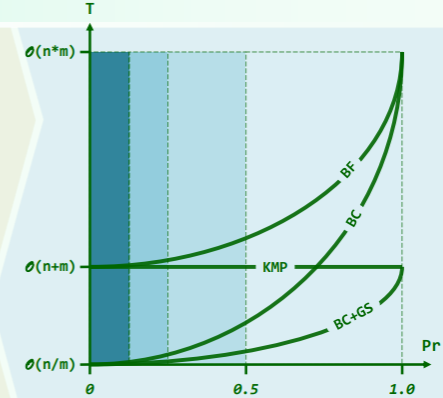
- 空间 = |bc| + |gs| = O (|Σ| + m)
- 预处理:O (|Σ| + m)
- 查找效率
- 最好 O (n / m)
- 最差 O (n + m) //分析方法类似 KMP
- 关键因素
- 单次比对成功的概率
- 通常,Pr = 1/s
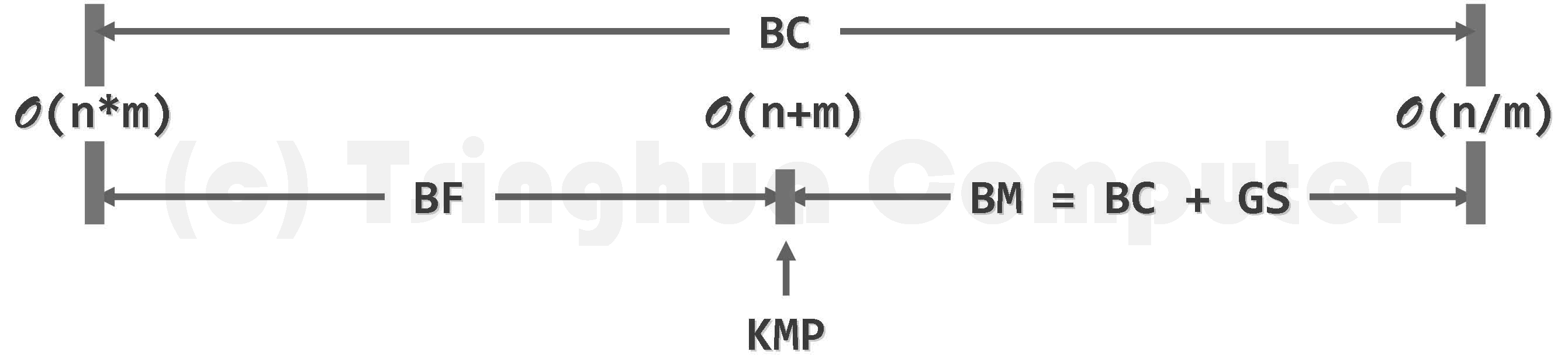
的提高,串匹配算法的运行时间(纵轴)通常亦将增加.png)
综合实例
i : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
P[i]: I C E D '' R I C E '' P R I C E
next[i]: -1 0 0 0 0 0 0 1 2 3 0 0 0 1 2
改进-next[i]: -1 0 0 0 0 0 -1 0 0 3 0 0 -1 0 0
bc[i]: 12 13 14 3 9 11 12 13 14 9 10 11 12 13 14
ss[i]: 0 0 3 0 0 0 0 0 4 0 0 0 0 0 15
gs[i]: 12 12 12 12 12 12 12 12 12 12 6 12 15 15 1
- 这里
gs[12..13]并没有在计算的情况中,之所以是 15,在于gs[]初始化时各元素为 P 串长度 m。
KR 法
凡物皆数思想
凡物皆数:Gödel Numbering(大名鼎鼎哥德尔)【毕导】这个视频里说的都是真的,但你却永远无法证明_哔哩哔哩_bilibili(数学之神的低语:sub (n, n, 17) 😈)
- 逻辑系统的符号、表达式、公式、命题、定理、公理等,均可表示为自然数
- 每个有限维的自然数向量(包括字符串),都唯一对应于某个自然数
- 素数序列:p (k) = 第 k 个素数 = 2, 3, 5, 7, 11, 13, 17, 19, …


- 十进制串,可直接视作自然数 //指纹(fingerprint),等效于多项式法
- P = “82818”, T = 27182818284590452353602874713527
- 一般地,随意对字符编号{ 0, 1, 2, …, d - 1 } //设 d = |∑|
- 于是,每个字符串都对应于一个 d 进制自然数 //尽管不是单射
- “CAT” = 2 0 19 (26) = 1371 (10) //∑ = { A, B, C, …, Z }
- “ABBA” = 0 1 1 0 (26) = 702 (10)
- P 在 T 中出现 仅当 T 中某一子串与 P 相等 //为什么不是“当”?
- 这,不已经就是一个算法了吗?! //具体如何实现?
- 问题似乎解决得很顺利,果真如此简单吗? //复杂度?
利用散列优化
如果|∑|很大,模式串 P 较长,其对应的指纹将很长,比如,若将 P 视作|P|位的|Σ|进制自然数,并将其作为指纹
- 仍以 ASCII 字符集为例 //|∑| = 128 = 27
- 只要|P| > 9,则指纹的长度将至少是:7 x 10 = 70 bits
- 然而,目前的字长一般也不过 64 位 //存储不便
- 而更重要地,指纹的计算与比对,将不能在 O (1)时间内完成 //RAM 的位数有限,因此超过 64 位的比对需要第二次比对,如果再过长则需更久
- 准确地说,需要 O (|P|/64) = O (m)时间;
- 总体需要
O(n*m)时间 //与蛮力算法相当 - 有何高招?
基本构思:
- 通过对比经压缩之后的指纹,确定匹配位置
- 关键技巧:通过散列,将指纹压缩至存储器支持的范围
- 比如,采用模余函数:hash ( key ) = key % 97
- P = 8 2 8 1 8 //hash (82818) = 77
- T = 2 7 1 8 2 8 1 8 2 8 4 5 9 0 4 5 2 3 5 3 6 2 7 1 8 2 //22 7 1 8 2 8 //48 1 8 2 8 1 //45 8 2 8 1 8 // 77
但是存在散列冲突问题:
- hash ()值相等,并非匹配的充分条件 //是必要条件
- 因此,通过 hash ()筛选之后,还须经过严格的比对,方可最终确定是否匹配
- P = 1 8 2 8 4 //hash (18284) = 48
- T = 2 7 1 8 2 8 1 8 2 8 4 5 9 0 4 5 2 3 5 3 6 2 7 1 8 2 //22 7 1 8 2 8 // 48 … 1 8 2 8 4 // 48
- 既然是散列压缩,指纹冲突就在所难免——好在,适当选取散列函数,极大降低冲突的概率
快速指纹计算
- hash ()的计算,似乎每次均需 O (|P|)时间 有可能加速吗?
- 回忆一下,进制转换算法,观察到
- 相邻的两次散列之间,存在某种相关性
- 相邻的两个指纹之间,也有某种相关性
- 利用上述性质,即可在 O(1)时间内 由上一指纹得到下一指纹…
 实际上,二者仅在首、末字符处有所出入。准确地如图11.21所示,前一子串删除首字符之后的后缀,与后一子串删除末字符之后的前缀完全相同。
实际上,二者仅在首、末字符处有所出入。准确地如图11.21所示,前一子串删除首字符之后的后缀,与后一子串删除末字符之后的前缀完全相同。
利用这种相关性,可以根据前一子串的指纹,在常数时间内得到后一子串的指纹。也就是说,整个算法过程中消耗于子串指纹计算的时间,平均每次仅为 O(1)。 该算法的具体实现,如代码所示:
// 子串指纹快速更新算法
void updateHash ( HashCode& hashT, char* T, size_t m, size_t k, HashCode Dm ) {
hashT = ( hashT - DIGIT ( T, k - 1 ) * Dm ) % M; //在前一指纹基础上,去除首位T[k - 1]
hashT = ( hashT * R + DIGIT ( T, k + m - 1 ) ) % M; //添加末位T[k + m - 1]
if ( 0 > hashT ) hashT += M; //确保散列码落在合法区间内
}
这里,前一子串最高位对指纹的贡献量应为 。只要注意到其中的 始终不变,即可考虑如下面代码所示,通过预处理提前计算出其对应的模余值。 为此尽管可采用快速幂算法 power2(),但考虑到此处仅需调用一次,同时兼顾算法的简洁性,故不妨直接以蛮力累乘的形式实现。
HashCode prepareDm ( size_t m ) { //预处理:计算R^(m - 1) % M (仅需调用一次,丌必优化)
HashCode Dm = 1;
for ( size_t i = 1; i < m; i++ ) Dm = ( R * Dm ) % M; //直接累乘m - 1次,幵叏模
return Dm;
}
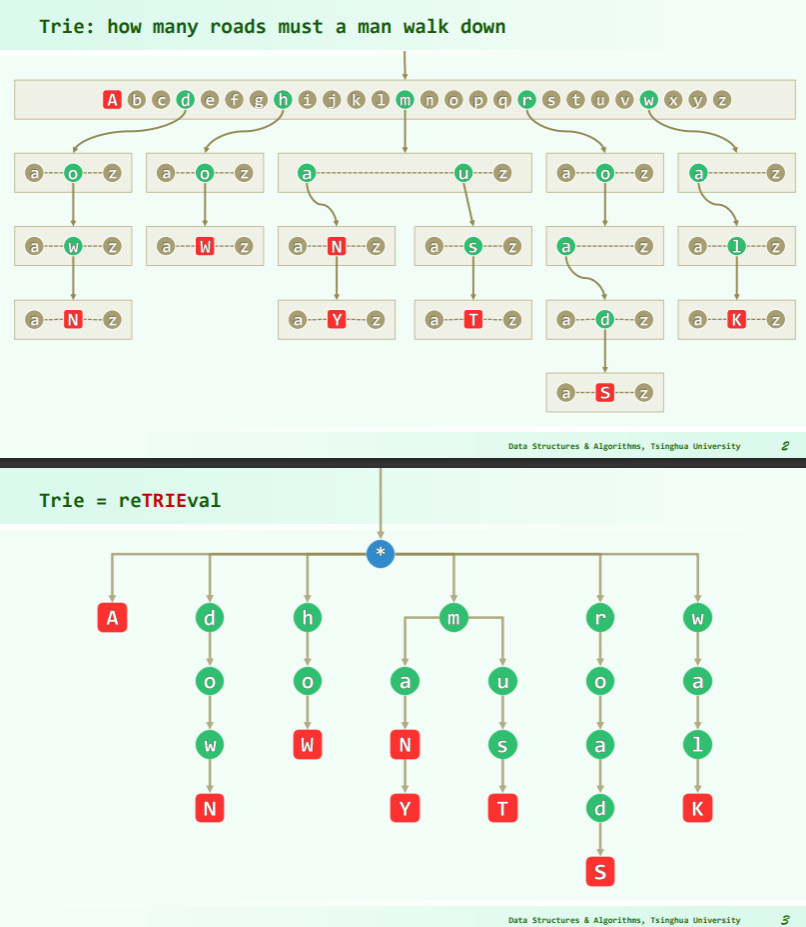
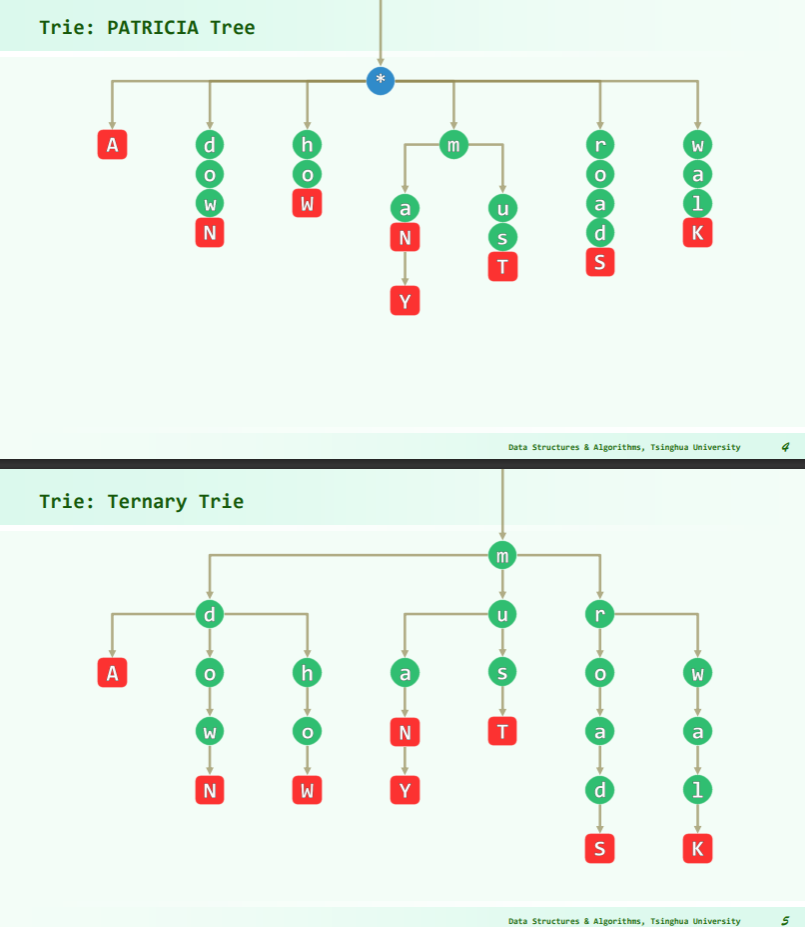
Trie 树
Trie = Digital Tree = Radix Tree = Prefix Tree