50-Training-versus-Testing

Recap and Preview

回顾一下之前所学：

• 第一堂课定义了机器学习的目标——找到对目标函数 $f$ 的最佳估计 $g$ ，
• 第二堂课分析了如何在训练集中找到正确的 $g$ ，
• 第三堂课列举了从不同角度看待机器学习并进行分类，
• 第四堂课验证了机器学习如何能够成立：

我们实际上将 ML 分为两个基本问题：

1. $E_{out}(g)$ 确实接近于 $E_{in}(g)$ 吗？
2. $E_{in}(g)$ 怎么做到足够小呢？

How the Size of Hypotheses Set Affects?

那么，假设集的大小 $M=|\mathcal{H}|$ 对这两个问题有何影响呢？

• 
• 因此，我们的基本理论还是 Hoeffding 不等式，并且希望找出一个合理大小的 M ，使得 $E_{out}(g)\approx E_{in}(g)$ ：

练习：需要多大的训练集？

Effective Number of Lines

Union Bound Probability Fail

现在，我们来讨论一下 M 究竟如何取值才合适吧。Hoeffding 不等式告诉我们：

$$\text{Prob}[|E_{in}(g)-E_{out}(g)|>ϵ]\le 2\cdot M\cdot e^{-2{ϵ}^{2}N}\text{\hspace{1em}(*)}$$

• 将 BAD events 记作 ${\mathcal{B}}_m:|E_{in}(h_m)-E_{out}(h_m)|>ϵ$ ，那么学习算法 $\mathcal{A}$ 进行选择出错的概率上界为 $\text{Prob}[{\mathcal{B}}_{1}or{\mathcal{B}}_{2}or...{\mathcal{B}}_M]$，
• 最坏情况就是所有 BAD events 都不重叠，即 $\text{Prob}[{\mathcal{B}}_{1}or{\mathcal{B}}_{2}or...{\mathcal{B}}_M]\le \text{Prob}[{\mathcal{B}}_1]+\text{Prob}[{\mathcal{B}}_2]+...+\text{Prob}[{\mathcal{B}}_M]$ 中的等号成立时，
• 然而事实上这种估计太过“不紧”，对于大多数问题，相邻的假设通常是重叠的，直接取并的操作过分地高估（over estimating）了上界：

因此我们需要对相似的、重叠的假设进行分组，重新评估出错的概率上界。

Infinite to finite

回顾之前平面里用直线进行二分的问题：

• 平面中的直线当然是无数多个，也即对应着 $M=|\mathcal{H}|=+\infty$，然而如果放入一个样本点 ${\mathbf{x}}_1$，那么直线就可以分为两类：
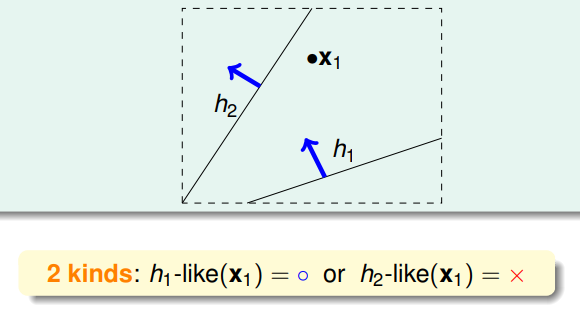
• 继续推广，如果两个样本点 ${\mathbf{x}}_1,{\mathbf{x}}_2$，则会有 4 种直线；如果三个样本点 ${\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3$，且三点不共线，则会有 8 种直线，如果三点共线，则会有 6 种直线：
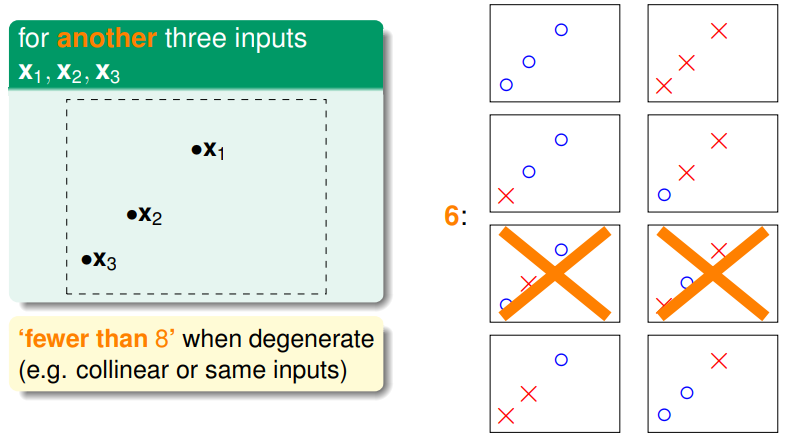
• 那么四个三三不共线的样本点 ${\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3,{\mathbf{x}}_4$ 呢？将会是 14 种：

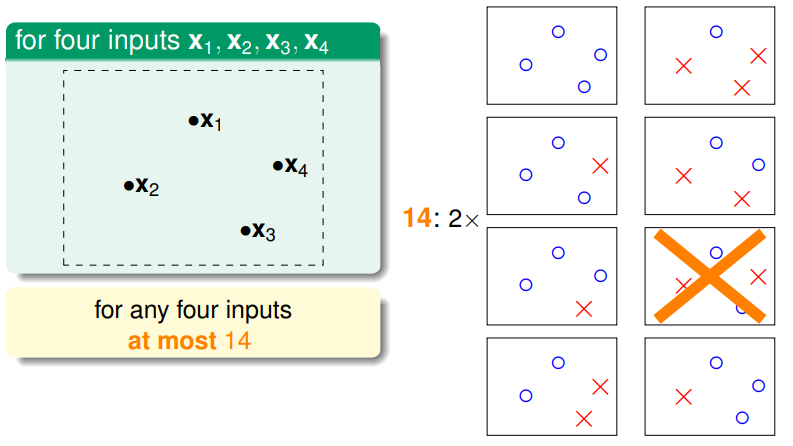
综上，我们将输入样本点数 $N$ 能够划分的直线的种数，称为 effective number of lines ，其一定 ≤ $2^N$ —— 我们完成了将无穷大的 $|\mathcal{H}|$ 分类、缩减到有限大小，且这个大小与输入样本数 $N$ 有关。于是，我们可以将 (*) 式中的 M 替换为：

$$\text{Prob}[|E_{in}(g)-E_{out}(g)|>ϵ]\le 2\cdot \text{effective}(N)\cdot e^{-2{ϵ}^{2}N}$$

，如果 $\text{effective}(N)$ 确实能够替换 M 且远小于 $2^N$，就能实现在无穷大的假设集 $\mathcal{H}$ 上实现有限分组的 learning 。如何找到这个 $\text{effective}(N)$ 呢？请看下文。

练习：划分五个样本的有效直线数

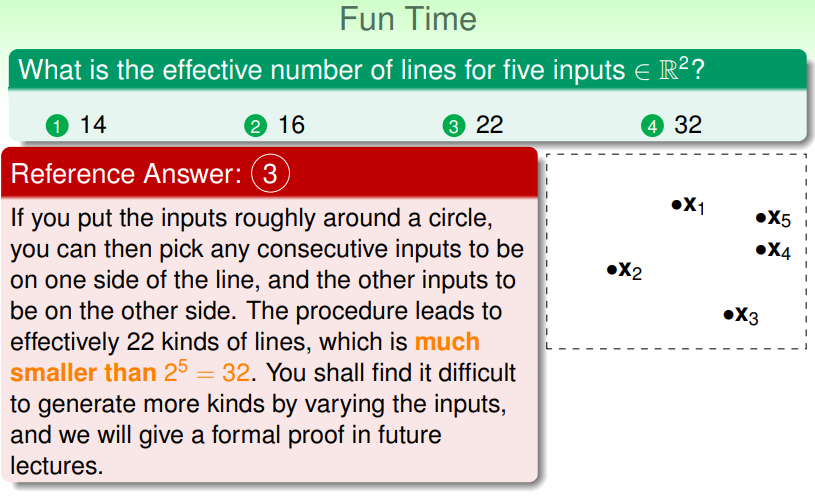
Effective Number of Hypotheses

Hypothesis set to Dichotomies

我们将二分问题的假设集定义为 $\mathcal{H}=\{\text{hypothesis }h:\mathcal{X}\to \{\times ,\circ \}\}$ ；而对若干个输入样本 ${\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_N$ 经过某一假设 $h$ 的分类，能够分为两堆，一堆输出为 $\times$ ，一堆输出为 $\circ$ ，这样产生的一个组合—— $h({\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_N)=(h({\mathbf{x}}_1),h({\mathbf{x}}_2),...,h({\mathbf{x}}_N))\in \{\times ,\circ {\}}^N$ ，称之为一个 Dichotomy（中文译作对分）。

那么将假设集 $\mathcal{H}$ 在输入样本 ${\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_N$ 上能够产生的 Dichotomy 的数量记作 $\mathcal{H}({\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_N)$，因此 Hypotheses 与 Dichotomies 的关系是这样：

• 
• Dichotomies 是只对有限数量的输入样本上划分的组合的数量，因此其有上界 $2^N$ ，于是我们将代替 M 的 $\text{effective}(N)$ 就可以替换为 Dichotomy 的数量 $|\mathcal{H}({\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_N)|$ 。

Growth Function

即使将 Hypotheses 简化成 Dichotomies ，其仍然取决于输入样本及其数量，而不同问题的输入样本千差万别，我们希望祛除对输入样本的依赖、找到能够通用的 $\text{effective}(N)$ 的形式：

• $m_{\mathcal{H}}=\underset{{\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_N\in \mathcal{X}}{\max }|\mathcal{H}({\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_N)|$ ，即从所有可能的输入样本 $({\mathbf{x}}_1,{\mathbf{x}}_2,...{\mathbf{x}}_N)$ 中取构成 Dichotomy 的数量的最大值，称为 Growth Function ；
• 由此得到仅含样本数 N 的函数关系式，从而将 $\text{effective}(N)$ 的上界限制为 $2^N$ 。

那么如何计算 Growth Function 呢？

1. 为了简化问题，先试想一维空间中的二分问题：
   • 此时，对每个 $a\in (x_n,x_{n+1})$ 是一个 dichotomy ，从而 $m_{\mathcal{H}}(N)=N+1\ll 2^N$
2. 而对于一维空间中区间选取问题：
   • 此时，每个区间的种类成为一个 dichotomy，从而 $m_{\mathcal{H}}(N)=\left(\genfrac{}{}{0ex}{}{N+1}{2}\right)+1=\frac{1}{2}{N}^2+\frac{1}{2}N+1\ll 2^N$ ，这里前者（组合数）意思是区间中至少包含一个输入样本，而后者 1 指区间中不包含任何样本；
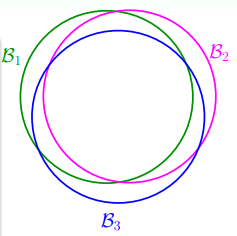
3. 再推广到二维空间的二分问题——判断输入样本是否在凸区域：
   • 此时，可以将输入的样本点视作一个圆周上的点，而处于凸区域的点为正，即以该圆周为外接圆的凸多边形的顶点，反之不在凸多边形上，
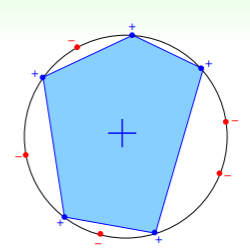
   • 那么每个多边形组成一个 dichotomy ，从而 $m_{\mathcal{H}}(N)=2^N$ ，此时在 ML 领域的术语中称为 those N inputs “shattered” by $\mathcal{H}$ ，shatter 本义是“打散”，在这里整体的意思所有可能都会被假设集 $\mathcal{H}$ 枚举出来。

练习：Growth Function 的计算

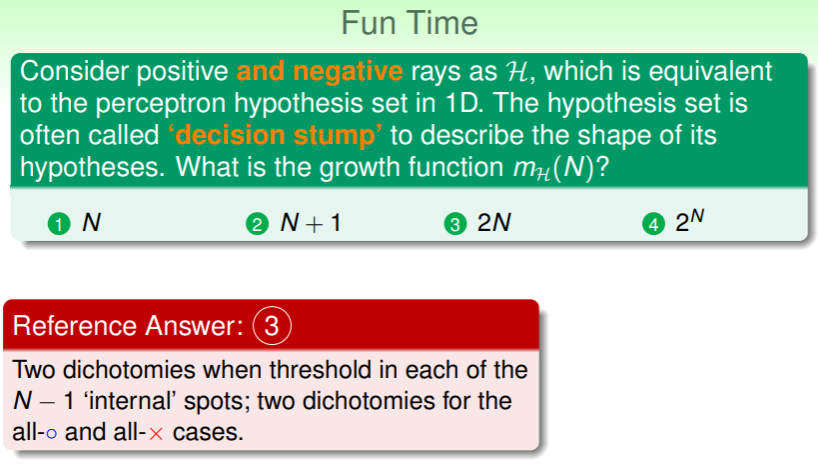
Break Point

在上一节我们得到了四种 Growth Function，然而如果直接用 $m_{\mathcal{H}}$ 取代 $\text{Prob}[|E_{in}(g)-E_{out}(g)|>ϵ]\le 2\cdot M\cdot e^{-2{ϵ}^{2}N}$ 中的 M ，还有一个时间复杂度的问题：

• 可以看到前两个是 $\mathcal{O}(N)$、$\mathcal{O}(N^2)$ 的多项式复杂度，第三个是 $\mathcal{O}(2^N)$ 的指数级复杂度，我们当然更希望多项式复杂度的 $m_{\mathcal{H}}$，那么该如何估计呢？

考虑二维平面中的有效直线数问题，

• 我们在 3 个输入样本时能够获得 $8=2^3$ 种有效直线，但是在 4 个输入样本时却只有 $14<2^4$ 种有效直线，而 5 个样本时只有 $22<2^5$ 种有效直线… 5 个及以上的样本必然可以由若干 4 个样本及其它数量的样本组成，那么必然满足 $m_{\mathcal{H}}(N)<2^N$ ；
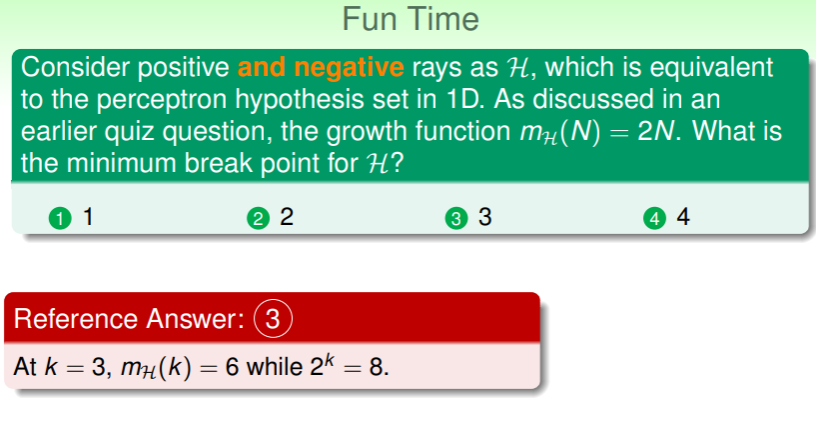
• 由这样的规律，我们将 4 这样的样本数称作 break point，即从此数开始的输入样本不能被假设集 $\mathcal{H}$ 完全 shatter；其中 4 为 minimum break point 。

考虑上述四个 $m_{\mathcal{H}}$ ，第一个的 break point 为 2，第二个为 3，第三个没有，第四个为 4，我们不妨大胆假设，对于 break point 为 k 时，$m_{\mathcal{H}}(N)=\mathcal{O}(N^{k-1})$ 。欲知证明若何，请看下节课。

练习：计算最小 break point