94-Priority-search-tree

In computer science, a priority search tree is a tree data structure for storing points in two dimensions. It was originally introduced by Edward M. McCreight.¹

It is effectively an extension of the priority queue with the purpose of improving the search time from O(n) to O(s + log n) time, where n is the number of points in the tree and s is the number of points returned by the search.

Description

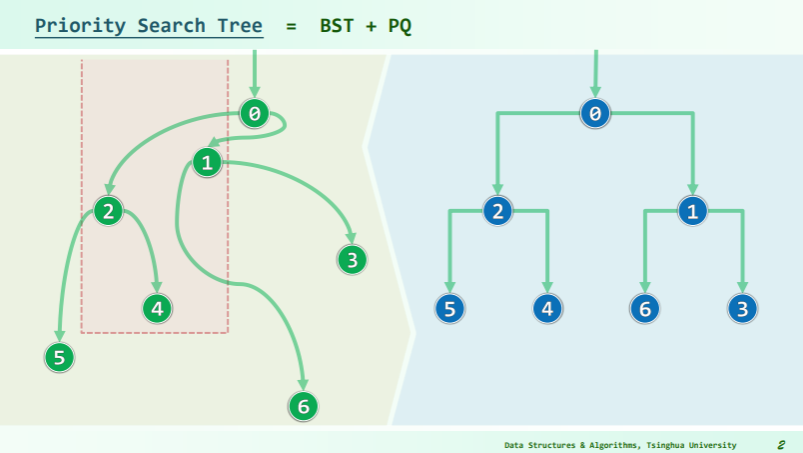
The priority search tree is used to store a set of 2-dimensional points ordered by priority and by a key value. This is accomplished by creating a hybrid of a priority queue and a binary search tree.

The result is a tree where each node represents a point in the original dataset. The point contained by the node is the one with the lowest priority. In addition, each node also contains a key value used to divide the remaining points (usually the median of the keys, excluding the point of the node) into a left and right subtree. The points are divided by comparing their key values to the node key, delegating the ones with lower keys to the left subtree, and the ones strictly greater to the right subtree.²

结果是一个树，其中每个节点表示原始数据集中的一个点。节点包含的点是优先级最低的点。此外，每个节点还包含一个键值，用于将剩余点（通常是键的中位数，不包括节点的点）划分为左右子树。通过将它们的键值与节点键进行比较来划分点，将键较低的键委派给左侧子树，将严格较大的键委派给右侧子树。

Operations

Construction

The construction of the tree requires O(nlogn) time and O(n) space. A construction algorithm is proposed below:

tree construct_tree(data) {
  if length(data) > 1 {
  
    node_point = find_point_with_minimum_priority(data) // Select the point with the lowest priority
    
    reduced_data = remove_point_from_data(data, node_point)
    node_key = calculate_median(reduced_data) // calculate median, excluding the selected point
    
    // Divide the points 
    left_data = []
    right_data = []    
   
    for (point in reduced_data) {
      if point.key <= node_key
         left_data.append(point)
      else
         right_data.append(point)
    }

    left_subtree = construct_tree(left_data)
    right_subtree = construct_tree(right_data)

    return node // Node containing the node_key, node_point and the left and right subtrees

  } else if length(data) == 1 {
     return leaf node // Leaf node containing the single remaining data point
  } else if length(data) == 0 {
    return null // This node is empty
  }
}

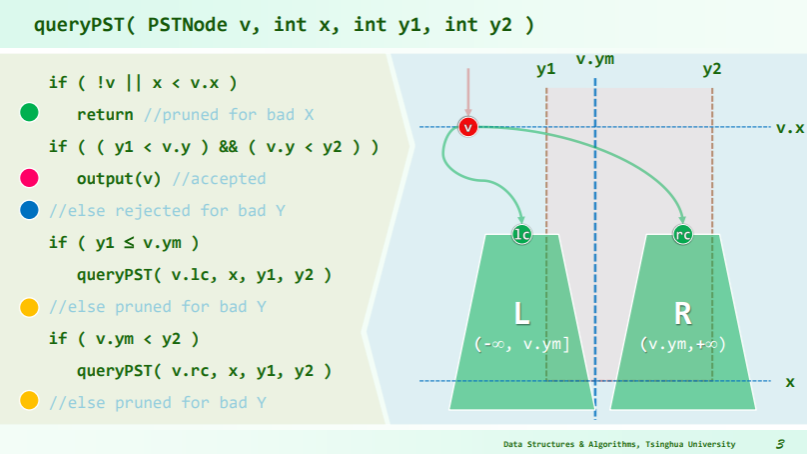
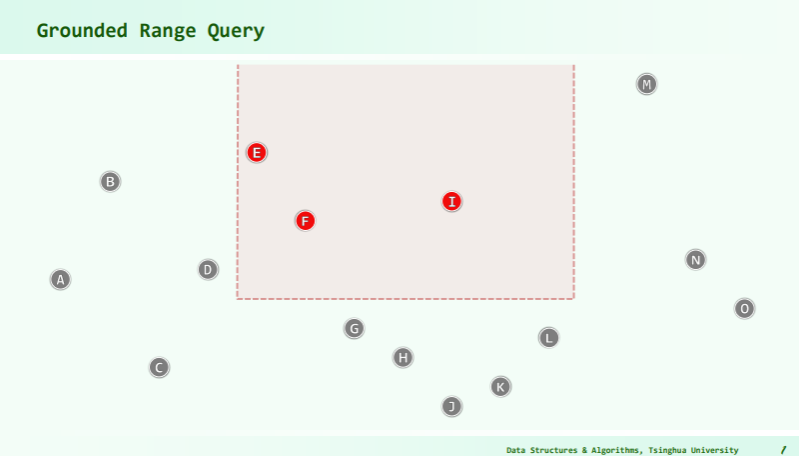
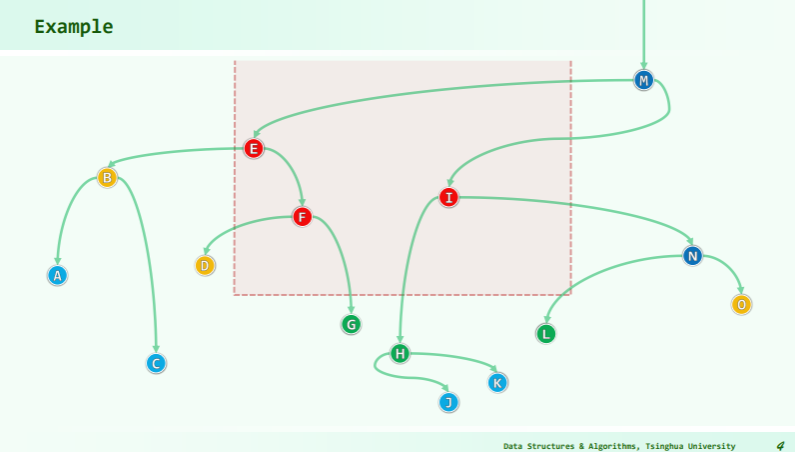
Grounded range search

The priority search tree can be efficiently queried for a key in a closed interval and for a maximum priority value. That is, one can specify an interval [min_key, max_key] and another interval [-∞, max_priority] and return the points contained within it.

This is illustrated in the following pseudo code:

points search_tree(tree, min_key, max_key, max_priority) {
  root = get_root_node(tree) 
  result = []
  
  if get_child_count(root) > 0 {
      
    if get_point_priority(root) > max_priority
      return null // Nothing interesting will exist in this branch. Return

    if min_key <= get_point_key(root) <= max_key // is the root point one of interest?
       result.append(get_point(node))
   
    if min_key < get_node_key(root) // Should we search left subtree?
        result.append(search_tree(root.left_sub_tree, min_key, max_key, max_priority))

    if get_node_key(root) < max_key // Should we search right subtree?
        result.append(search_tree(root.right_sub_tree, min_key, max_key, max_priority))
      
    return result

  else { // This is a leaf node
    if get_point_priority(root) < max_priority and min_key <= get_point_key(root) <= max_key // is leaf point of interest?
       result.append(get_point(node))
  }
}

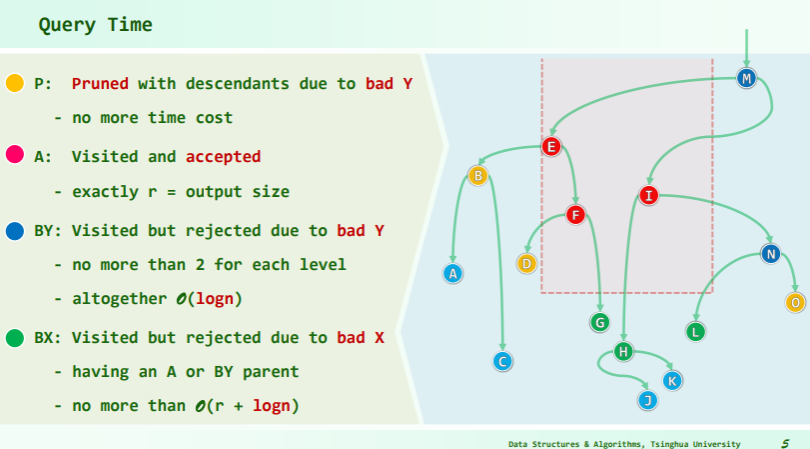
Quert time

Footnotes

1. McCreight, Edward (May 1985). “Priority search trees”. SIAM Journal on Scientific Computing. 14 (2): 257–276. doi: Priority Search Trees | SIAM Journal on Computing. ↩

2. Lee, D.T (2005). Handbook of Data Structures and Applications. London: Chapman & Hall/CRC. pp. 18–21. ISBN 1-58488-435-5. ↩