2016-final

判断

1. 若 AVL 树插入元素的过程中发生了旋转操作，则树高必不变。

❌

✅ AVL 树失衡后通过调整必回复原⾼度（如果没出现失衡，则树⾼可能发⽣改变）

2. 若红黑树插入一个元素后，黑高度增加，则双红修正过程中没有拓扑结构变换，只有重染色操作。

❌

✅ 双红修正 RR-2: 双红修正

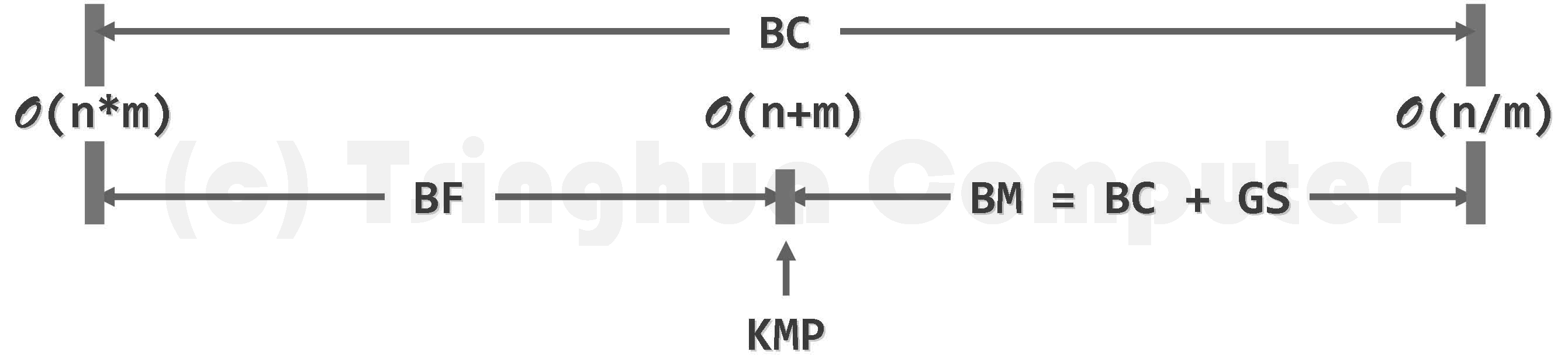
3. 若 KMP 算法不使用改进版的 next 表，最坏情况下时间复杂度可能达到 O(mn)。

❌ 最坏情况下也不过 O(m+n)

4. 在 BST 中删除两个节点，则无论先删除哪个节点，最终 BST 的拓扑结构均相同。

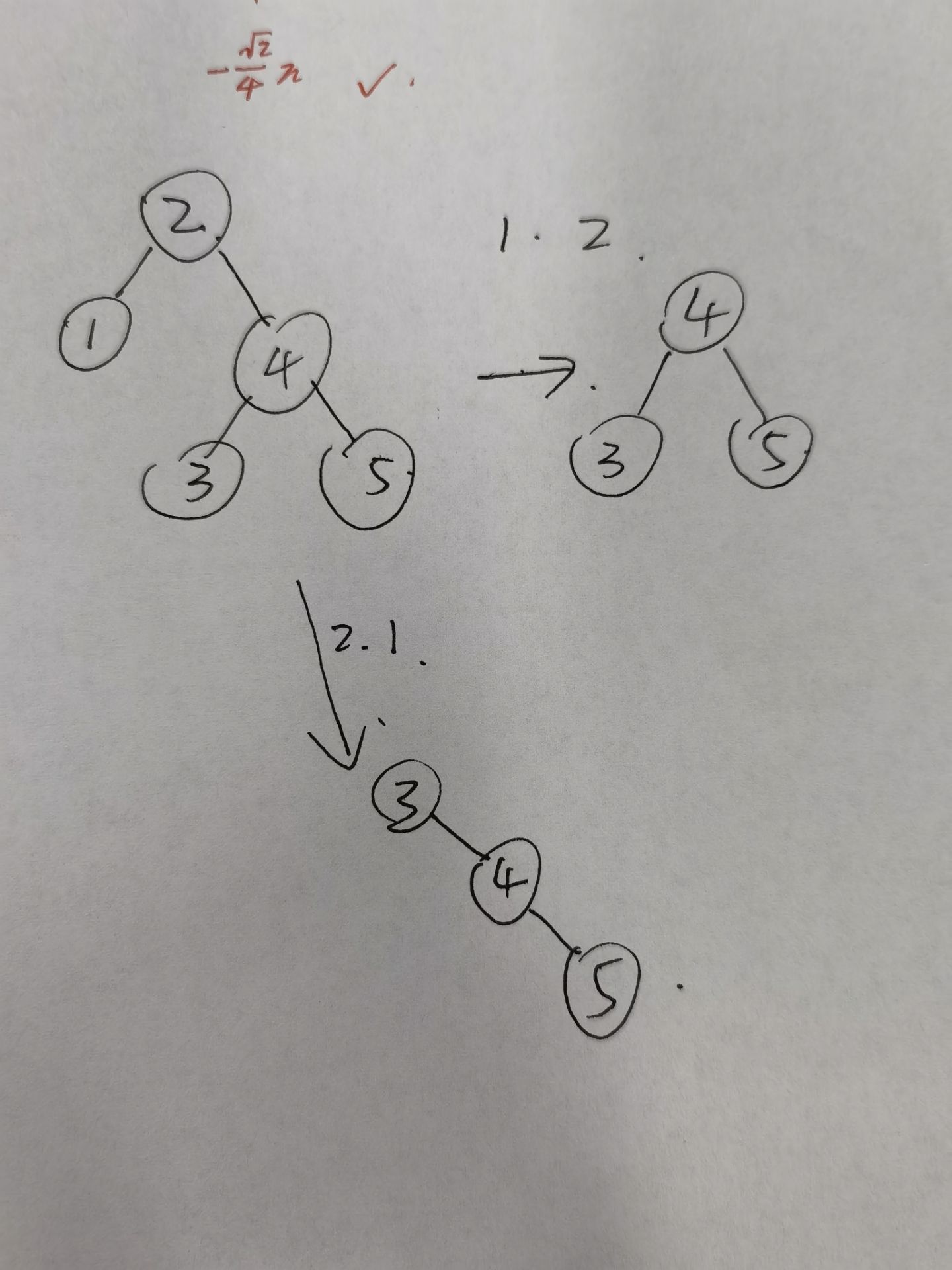
❌ splay 树中的删除操作会改变整体的形态，实例如下： 原 Splay tree： 删除 8、4 后的形态： 删除 4、8 后的形态： 事实上即使是 BST 也是不能保证的：

5. 完全二叉堆删除元素在最坏情况下时间复杂度为 O(log n)，但平均情况下仅为 O(1)。

❌ 完全二叉堆插入的平均复杂度可以是 O (1)，但删除并不可以。删除操作由于是将底层节点放置顶层再下滤，那么由于底层通常数据较小，会造成多次下滤。

6. 在任何情况下，伸展树总能保持每次操作 O(log n) 的平均复杂度。

✅

7. 对于左式堆 A 和 B，合并后所得二叉堆的右侧链元素一定来自 A 和 B 的右侧链。

❌ 左式堆只是保证左倾侧，但是并不能保证右子堆一定比左子堆小，由此导致左右子堆可能会交换。

8. 如果元素理想随机，那么对二叉搜索树做平衡化处理，对改进其渐进时间复杂度并没有什么卵用。

✅

9. 采用双向平方试探策略时，将散列表长度取作素数 M = 4k + 3，可以极大地降低查找链前 M 个位置冲突的概率，但仍不能杜绝。

❌ 4k+3的素数表长并使用双向平方试探策略，在前 M 个位置不会遇到冲突。

10. 在使用 Heapify 批量建堆的过程中，改变同层节点的下滤次序对算法的正确性和时间效率都无影响。

✅ 习题 10-7：10-7 Floyd 建堆法中同层内部节点下滤次序的影响

11. 在 kd-search 中，查找区间 R 与任一节点的 4 个孙节点（假设存在）对应区域最多有 2 个相交。

✅ (考研不考) 习题解析 8-16：[[62-BST-Exercise#8-16-kdsearch-的结论证明|8-16 kdSearch() 的结论证明]] 书上的结论写的是四个孙节点中的⾄多两个节点会相交（注意这⾥对相交的定义）

12. 在 n 个节点的跳转表中，塔高的平均值为 O(log n)。

❌ 塔高期望为 2

13. 既然可以在 O(n) 时间内找出 n 个数的中位数，快速排序算法 (12-A1) 即可优化至 O(nlogn)。

✅

14. 将 N 个关键码按随机次序插入 B 树，则期望的分裂次数为 $O(\log N)$。

✅ 习题 8-6：8-6 考查 BTree 节点插入导致的分裂次数

15. 与二叉堆相比，多叉堆 delMax() 操作时间复杂度更高。

✅ 老问题，还是考虑三叉对和四叉堆这两个特殊情况。

16. 若元素理想随机，则用除余法作为散列函数时，即使区间长度不是素数，也不会影响数据的均匀性。

✅ PPT 除余法那一节：M 不是素数可以吗？

17. 与胜者树相比，败者树在重赛过程中，需反复将节点与其兄弟进行比较。

❌ 正好搞反

18. 在图的优先级搜索过程中，每次可能调用多次 prioUpdater，但累计调用次数仍为 O(e)。

✅ 调用 prioUpdater 与否，取决于邻居的总数，因此也就是边的总数。

19. 若序列中逆序对个数为 O(n^2)，则使用快速排序 (12-A1) 须进行的交换次数为 O(nlogn)。

❌ 完全逆序时，逆序对个数为 $O(n^2)$，但是快排需要的交换次数也为 $O(n^2)$

20. 如果把朋友圈视为一无向图，那么即使 A 君看不到你给 B 点的赞，你们仍可能属于同一个双联通分量。

✅ “我”是关节点

选择

1. 二叉堆中某个节点秩为 k，则其兄弟节点（假设存在）的秩为（ D ）

A. k + 1 B. k − 1 C. k + (−1)^k D. k − (−1)^k E. 以上皆非

兄弟节点只存在于同一父亲下，又由于是二叉堆，因此兄弟只会有一个。

2. 由 5 个互异节点构成的不同的 BST 共有（ D ）个 A. 24 B. 30 C. 36 D. 42 E. 120

Catalan(5) = 42

3. 有 2015 个节点的左式堆，左子堆最小规模为（ ）（不计外部节点） A. 10 B. 11 C. 1007 D. 1008 E. 以上皆非

E. 可以是 1

4. 与 MAD 相比，除余法在（ B, C ）有缺陷 A. 计算速度 B. 高阶均匀性 C. 不动点 D. 满射性 E. 以上皆非

MAD 改善了零阶均匀和不动点问题。 除余法中存在着两方面的缺陷：

• 不动点：无论表长 M 取值如何，总有 hash（0）= 0
• 零阶均匀：[0, R) 的关键码，平均分配至 M 个桶；但相邻关键码的散列地址也必相邻

5. 以下数据结构，在插入元素后可能导致 O (log n) 次局部结构调整的是（ B, D ） A. AVL B. B-树 C. 红黑树 D. 伸展树 E. 以上皆非

AVL 插入元素只会导致 O (1)次局部调整 B-tree 插入元素可能导致一直上溢分裂到根，即 O (logn)次调整 红黑树局部结构调整不会超过 O (1) 伸展树插入元素会放置到根部，也是 O (logn)次调整

6. 对小写字母集的串匹配，KMP 算法与蛮力算法在（ A, C ）情况下渐进的时间复杂度相同 A. 最好 B. 最坏 C. 平均 D. 以上皆非

平均情况的细致分析可以看习题 11-9：11-9 分析蛮力算法的实际效率

7. 对随机生成的二进制串，gs 表中 gs[0]=1 的概率为（ ） A. $\frac{1}{2^m}$ B. $\frac{1}{2^{m-1}}$ C. $\frac{1}{2^{m+1}}$ D. $\frac{1}{m}$

不会 答案给出的解析：B. 所有元素相等时

8. 以下数据结构，空间复杂度为线性的是（ A ） A. 2d-tree B. range tree C. interval tree D. segment tree E. 以上皆非

A, C, D

9. 人类拥有的数字化数据数量，在 2010 年已达到 ZB (2^70 = 10^21) 量级。若每个字节自成一个关键码，用一颗 16 阶 B-树存放，则可能的高度为（ B ） A. 10 B. 20 C. 40 D. 80 E. >80

$\lceil {\log }_{16}(2^{70}+1)\rceil \le h\le 1+\lfloor {\log }_8(\frac{2^{70}-1}{2})\rfloor$ = 18~23

10. 在 BST 中查找 365，以下查找序列中不可能出现的是（ B, D ） A. 912, 204, 911, 265, 344, 380, 365 B. 89, 768, 456, 372, 326, 378, 365 C. 48, 260, 570, 302, 340, 380, 361, 365 D. 726, 521, 201, 328, 384, 319, 365

B 372→326→378 这里违背了 BST 左子树小于子树根节点的规则 D 328→384→319 同理

综合

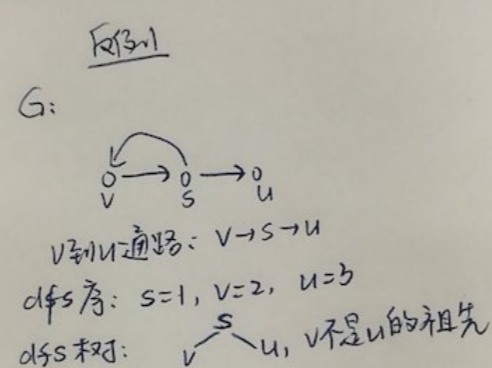
1. 在有向图 G 中，存在一条自顶点 V 通向 u 的路径，且在某次 DFS 中有 dTime[v]<dTime[u]，则在这次 DFS 所生成的 DFS 森林中，v 是否一定是 u 的祖先？若是，请给出证明； 若不是，请举出反例。

不是。

2. 对闭散列 [0, M)，$M=2^S$，采用如下冲突排列解决方法：
   • 初始时，c = d = 0
   • 探查 key 冲突时，c <- c + 1，d <- d + c，探查 H[(key+d)%M]
   • 则这种算法是否可以保证空间能被 100% 利用？若是，请给出证明；若不是，请举出反例。

d 的探查序列为：0+1,1+2,3+3,6+4,10+5,… 由递推公式 $d_{n+1}=d_n+n$，解得 $d_n=\frac{n^2+n}{2}$ 如果设置表长为 8，则秩为 0，1，2，3，5，6，7 的位置会有元素填入，但秩为 4 的地方永远没有元素，故不能保证 100% 利用。

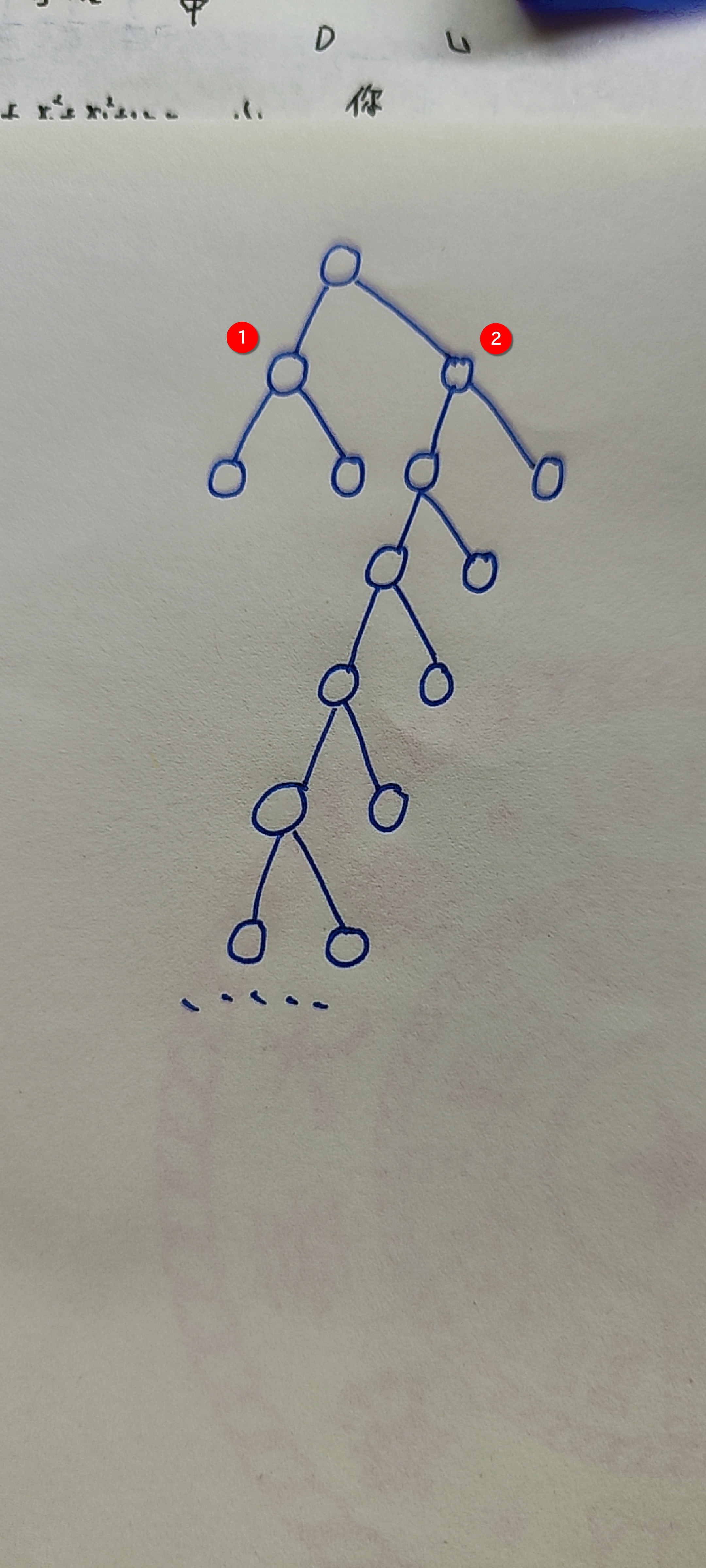
3. 在不改变 BST 和 BinNode 定义的前提下（BinNode 仅存储 parent, data, lc, rc），设计算法，使得从节点 x 出发，查找值为 Y 的节点 y 的时间复杂度为 o (d)， d 为节点 x 与 y 的距离。要求利用树的局部性，复杂度与总树高无关，否则将不能按满分起评。函数定义式：参量为 BinNode x, y, T，返回值为 BinNode 类型，函数名 fingerSearch。 (a) 说明算法思路

fingersearch：69-Finger-Search 简要地说，若搜索目标 y<起始节点 x，则向左搜索目标，具体地可以先搜索 x 的左子树，若左子树中存在则返回，若左子树中找到小于 y 的节点，则从对应节点的右子树开始搜索；若在 x 的左子树中未找到，则找到 x 的父亲，然后从 x 的父亲向左继续搜索，直到确定不大于 y 的最大者。

(b) 写出伪代码

(c) 在图中画出由值为 6 的点查找值为 17 的点的查找路径

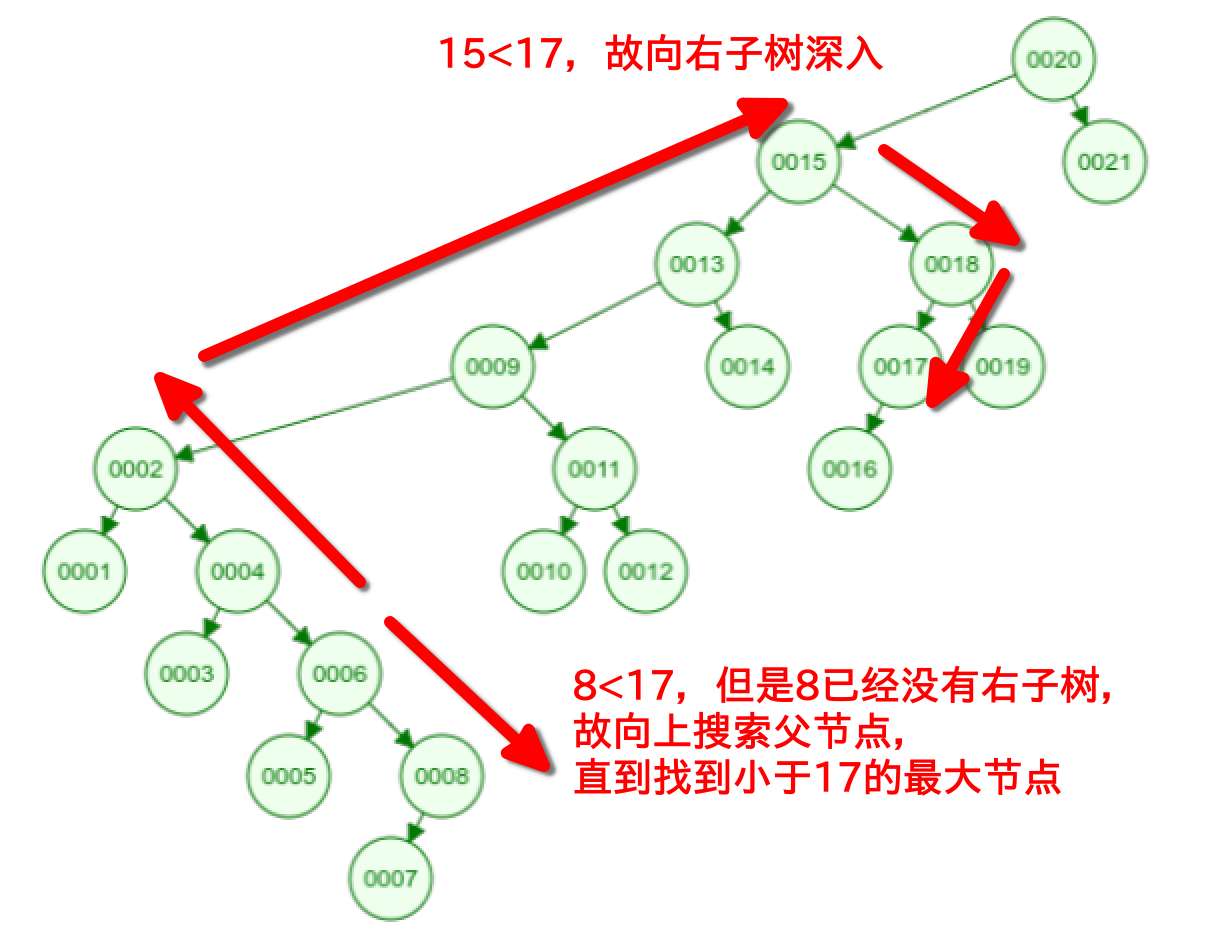
(d) 说明算法时间复杂度为 O(d)（若无法达到，说明困难在哪）

显而易见，非路径上的节点，遍历的数量非常有限。