Restriction of Break Point
上节课 我们猜测了 break point 对 的数量级的估计,那么 break point 究竟如何限制其增长的呢?
来讨论这样的情形:当 minimum break point 时,意味着任意两个输入样本,都不能被假设集 完全 shatter,
- 那么当输入样本数 时,;当 时,;当 时呢?
 此时 ,
此时 , - 可以看出,break point k 极大程度地限制了 可以取得的最大值,回想之前的猜测,
练习:k=1 时的 最大值
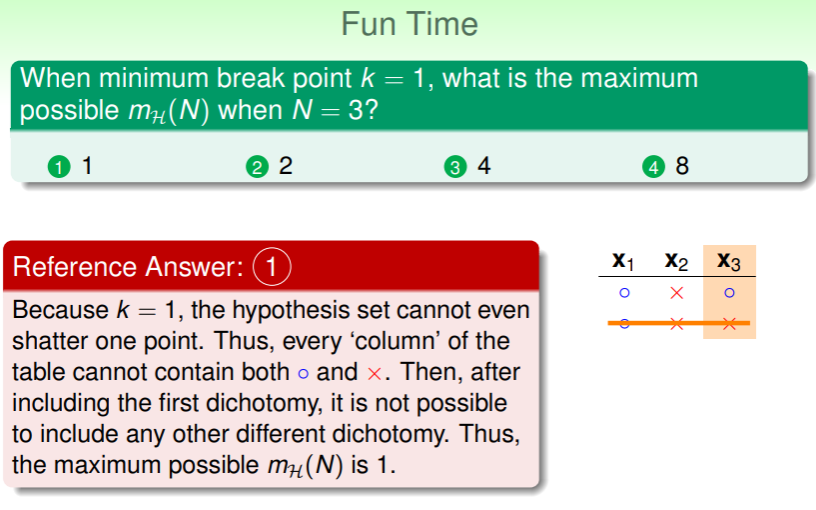
Bounding Function: Basic Cases
我们定义 bounding function —— ,如果能够判断 ,那么之前对 的估计也就必然成立:
- 实际上是一个组合数,其等于 元素都只取自 的、长度为 N 的、不能被长度为 k 的子向量所 shatter 的向量的数量 ;
- 实际上与假设集 的具体内容无关,例如 既可以表示 positive intervals 问题,又可以表示 1D perceptrons 问题,越抽象的函数越是需要少的依赖;
- 如此,我们可以填写这样的表以期找出 的关系:
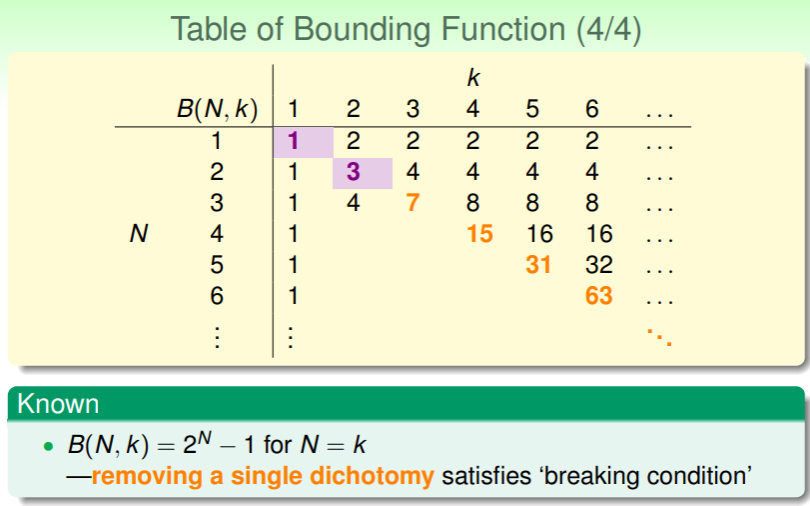
Bounding Function: Inductive Cases
现在,我们来尝试找出上面矩阵的下半三角部分的规律: 表示 4 个输入样本时,那么必然与 3 个输入样本有关,我们尝试找出 与 的关系:
.png)
- 注意这里 dichotomies set 的数量为 ,是怎么算出来的呢?一个 dichotomy 中有 4 个元素,故有 种 dichotomy,而 dichotomies set 是指 dichotomy 有几种选择方法,故总共 种;
- 对这 11 种 dichotomy 进行分类:
 其中橙色部分是两两有 3 个元素完全相同的,而紫色部分则没有;
其中橙色部分是两两有 3 个元素完全相同的,而紫色部分则没有; - 记 ,其中 表示 3 个输入样本 时 dichotomies 的数量,
 于是将 表示的不能由 3 个子向量 shatter 的问题 缩小 为在 3 个输入中不能被 3 个长度的子向量 shatter 的问题,即 ;
于是将 表示的不能由 3 个子向量 shatter 的问题 缩小 为在 3 个输入中不能被 3 个长度的子向量 shatter 的问题,即 ; - 更进一步地, 表示对成对的 来说,在输入样本 上 dichotomies 的数量,
.png) 从而 又缩小为 3 个输入中不能被 2 个长度的子向量 shatter 的问题,即 ;
从而 又缩小为 3 个输入中不能被 2 个长度的子向量 shatter 的问题,即 ; - 将这两个不等式联立,我们可以得知:
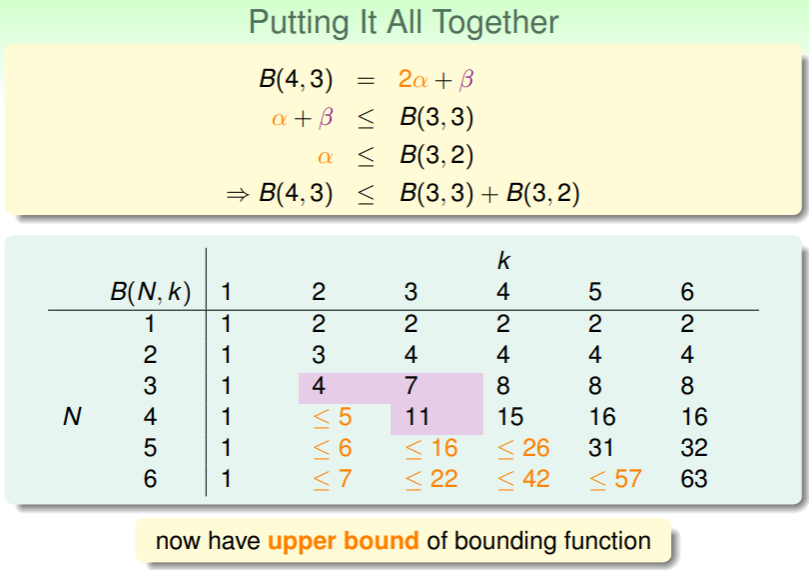 代换其中的 4 和 3,我们得到 这个递推关系式,即 的上界的上界;
代换其中的 4 和 3,我们得到 这个递推关系式,即 的上界的上界;
推导递推关系式,可以得到这样的关于 N 和 k 的关系式: 。(另外 其实可以在数学上证明为 )
如此,我们完成了证明:只要 break point 存在,那么 必然是多项式复杂度的:
练习:理解 的上界

A Pictorial Proof: VC-bound
现在,我们能够直接使用 来代替原来的 M 了吗?实际上,还差一些,经过 ML 前辈的推导,当 足够大时,关系式变成了这样:
这个关系式由 Vapnik-Chervonenkis 发现,于是命名为 VC-bound 公式,其证明步骤比较麻烦,总的来说可以分成三步:
- 化未知为已知:
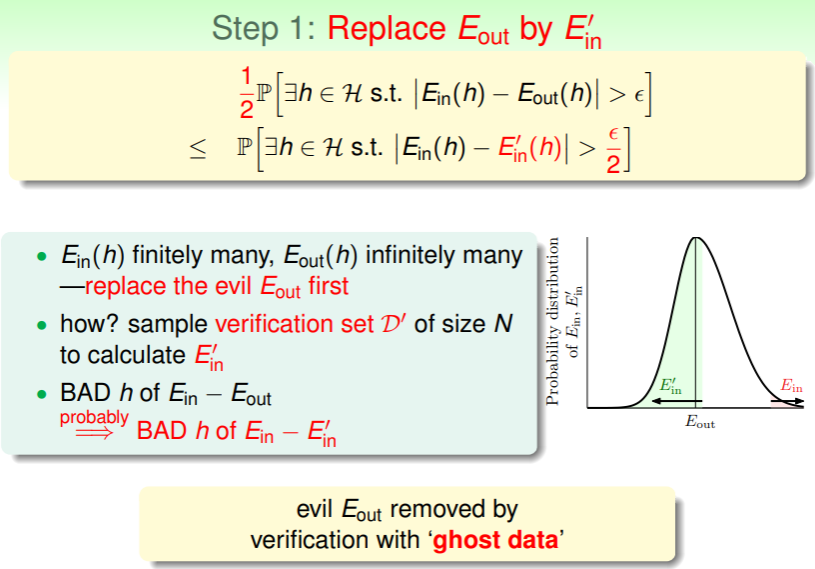
- 将无穷大的假设集 分类为有限种:
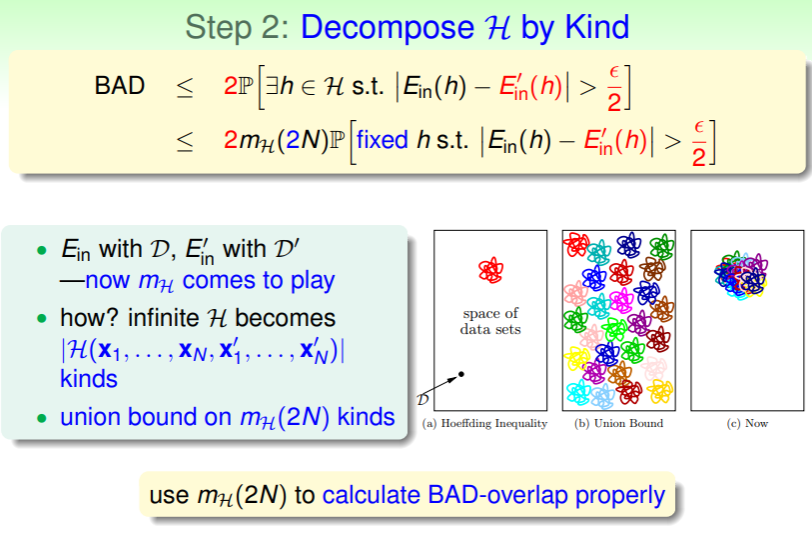
- 利用 Hoeffding 不等式消去 Prob 关系式:

练习:VC-bound 使用

