40-Soft-Margin-Support-Vector-Machine

Motivation and Primal Problem

Soft-Margin SVM

前三节讨论的都是 Hard-Margin SVM ，即要求所有对样本的判断都要正确：

$$\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\text{ s.t. }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\ge 1,\text{for all }n$$

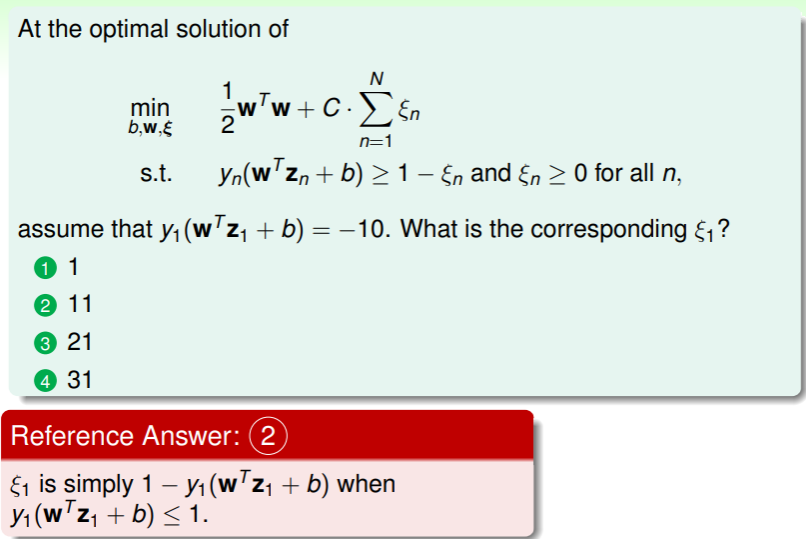
这样的缺点就是在有噪音的数据集中，会导致过拟合现象发生：

因此，为了避免过拟合现象，我们必须考虑舍弃这些噪音样本。回想 pocket 算法中对噪音样本的处理：$\underset{b,\mathbf{w}}{\min }\sum _{n=1}^N[y_n\ne \text{sign}({\mathbf{w}}^T{\mathbf{z}}_n+b)]$ ，我们可以结合 pocket 和 hard-margin SVM ，以实现对噪音容忍的 soft-margin SVM ：

$$\begin{array}{rl}& \underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\cdot \sum _{n=1}^N[y_n\ne \text{sign}({\mathbf{w}}^T{\mathbf{z}}_n+b)]\\ & \text{ s.t. }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\ge 1,\text{for correct }n\\ & y_n({\mathbf{w}}^T{\mathbf{x}}_n+b)>-\infty ,\text{ for incorrect }n\end{array}$$

• 这里目标中的 $C$ 作用是对 SVM 的 margin 宽度和噪音容忍度的权衡，
• 限制条件中对正确的样本点要判断正确，而对噪音点的样本判断结果不至于过大；

Solution of Soft-Margin SVM

对 soft-margin SVM 的假设仔细察看，可以很容易发现，这里 $[y_n\ne \text{sign}({\mathbf{w}}^T{\mathbf{z}}_n+b)]$ 并不是线性的条件，它是对每个样本的 label 和预测的正误判断，因此就不是 QP 问题，而之前讨论的 Dual SVM 、Kernel SVM 在这里也就不再适用。😢

并且，我们这样笼统地说判断结果与实际 label 的差异不致于过大（即， $>-\infty$），这也未免太过宽松。毕竟，有的预测可能仅与 boundary 差距毫厘，而有的预测却谬之千里，我们上面的 soft-margin SVM 不能很好地区分这两种预测错误，因此势必要对 soft-margin SVM 的假设做进一步改进。

我们提出对判断与 label 差距程度的考量，即 margin violation ，记作 ${\xi }_n$ ，通过对 margin violation 的惩罚代替犯错数的限制，从而转化为 linear constraints 的 QP 问题。于是 soft-margin SVM 的假设修改为：

$$\begin{array}{rl}& \underset{b,\mathbf{w},\xi }{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\cdot \sum _{n=1}^N{\xi }_n\\ & \text{ s.t. }{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)\ge 1-{\xi }_n,\text{and }{\xi }_n\ge 0\text{ for all }n\end{array}$$

这里 $C$ 的作用仍然没有变化，但是更进一步地可以理解为调节 margin length 和 margin violation 的权重：

• 大 $C$ 代表对噪音的容忍度更低；
• 而小 $C$ 代表更大的 margin ，提高对噪音的容忍度；

于是，soft-margin SVM 就转化为 $\tilde{d}+1+N$ 个变量、$2N$ 个条件限制的 QP 问题，我们可以从此推导出 Dual Soft-Margin SVM ，进行更细致的考量。

练习：理解 margin violation

Dual Problem

实现 soft-margin SVM 的对偶问题转化，同样离不开拉格朗日函数：

$$\begin{array}{rl}\mathcal{L}(b,\mathbf{w},\xi ,\alpha ,\beta )=& \frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{n=1}^N{\xi }_n\\ & +\sum _{n=1}^N{\alpha }_n\cdot \left(1-{\xi }_n-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b)\right)+\sum _{n=1}^N{\beta }_n\cdot (-{\xi }_n)\end{array}$$

• 这里 ${\alpha }_n,{\beta }_n$ 即是计算拉格朗日函数的两个限制的系数；

同理，我们要得到的拉格朗日对偶问题，形式如下：

$$\begin{array}{rl}& \underset{{\alpha }_n\ge 0,{\beta }_n\ge 0}{\max }\left(\underset{b,\mathbf{w},\xi }{\min }\mathcal{L}(b,\mathbf{w},\xi ,\alpha ,\beta )\right)\end{array}$$

类似地，我们要求解这个对偶问题，首先要进行化简。先要在 $\mathcal{L}(b,\mathbf{w},\xi ,\alpha ,\beta )$ 中找到极小值，因此极小点处有：

$$\frac{\partial \mathcal{L}}{\partial {\xi }_n}=0=C-{\alpha }_n-{\beta }_n$$

和之前一样，我们按图索骥：直接将 $C-{\alpha }_n-{\beta }_n=0$ 作为限制，于是可以移除拉格朗日对偶问题中的 ${\xi }_n$ ：

$$\begin{array}{rl}& \underset{0\le {\alpha }_n\le C,{\beta }_n=C-{\alpha }_n}{\max }\left(\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+\sum _{n=1}^N{\alpha }_n(1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b))\right)\end{array}$$

• 这里之所以 ${\alpha }_n$ 的限制变为 $0\le {\alpha }_n\le C$ ，是因为 ${\beta }_n$ 发生了变化，并且要保证 ${\alpha }_n\ge 0,{\beta }_n\ge 0$ ；

Simplify Lagrange Dual

现在，我们再细细查看简化后的拉格朗日对偶问题，似乎和之前 Dual hard-margin SVM 有些相似？仔细对比，实际上二者差异仅仅是限制条件，因此我们可以依葫芦画瓢，进一步实现化简：

• 由于极小值点 $\frac{\partial \mathcal{L}}{\partial b}=0$ ，因此我们可以得到限制条件 $\sum _{n=1}^N{\alpha }_n{y}_n=0$ ；
• 并且 $\frac{\partial \mathcal{L}}{\partial w_i}=0$ ，我们可以得到限制条件 $\mathbf{w}=\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n$ ；

因此，最终化简后的 Soft-Margin SVM Dual 为：

$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{n=1}^N\sum _{m=1}^N{\alpha }_n{\alpha }_m{y}_n{y}_m{\mathbf{z}}_n^T{\mathbf{z}}_m-\sum _{n=1}^N{\alpha }_n\\ & \text{ s.t. }\sum _{n=1}^N{y}_n{\alpha }_n=0,0\le \alpha \le C\text{ for n}=1,2,...,N\end{array}$$

• 其中暗含的条件就是 $\mathbf{w}=\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n$ 和 ${\beta }_n=C-{\alpha }_n,\text{for }n=1,2,...,N$

这样，我们通过对偶问题的转化，得到了仅有 $N$ 个变量、$2N+1$ 个限制的 QP 问题。

练习：理解 primal 问题中 C 的影响

Message behind Soft-Margin SVM

得到对偶 soft-margin SVM 后，我们就能照例引入 kernel function 来进一步祛除对 $\tilde{d}$ 的依赖，现在 kernel soft-margin SVM 的计算流程如下：

• 
• 这与 hard-margin SVM 的 kernel 形式几乎一致，不过在边界处理和对噪音点处理上更加灵活；

Determine Parameter $b$

不过上图中有一个参数的确定与 hard-margin SVM 不太一样，那就是 $b$ 。回想 hard-margin SVM 的参数 $b$ 的求解过程，在 KKT 条件下，要从如下条件中解出 $b$ ：

$${\alpha }_n(1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b))=0$$

因此只要找到任意一个 ${\alpha }_n>0$ 的 SV ，就可以求得 $b=y_n-{\mathbf{w}}^T{\mathbf{z}}_n$ 。类似地，要从如下条件的 soft-margin SVM 中解出 $b$ ：

$$\begin{array}{r}{\alpha }_n(1-{\xi }_n-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b))=0\\ (C-{\alpha }_n){\xi }_n=0\end{array}$$

除了要满足 ${\alpha }_n>0$ 才能得到 $b=y_n-y_s{\xi }_s-{\mathbf{w}}^T{\mathbf{z}}_s$ 外，还要满足 $C-{\alpha }_n>0$ ，即 margin violation 的程度 ${\xi }_s=0$ ，这意味着是在 soft-margin SVM 的 boundary 内部的 SV ，通常称为 free SV 。

因此，综合起来，求解 soft-margin SVM 中参数 $b$ 的方法是：对任意 free SV $({\mathbf{x}}_s,y_s)$ ，求得：

$$b=y_s-\sum _{\text{SV indices }n}{\alpha }_n{y}_{n}K({\mathbf{x}}_n,{\mathbf{x}}_s)$$

Role of Parameter $C$

另一方面，soft-margin SVM 中参数 $C$ 的直观意义是如何呢？

• 通过 Gaussian Kernel Function 简化的 soft-margin SVM 如下：
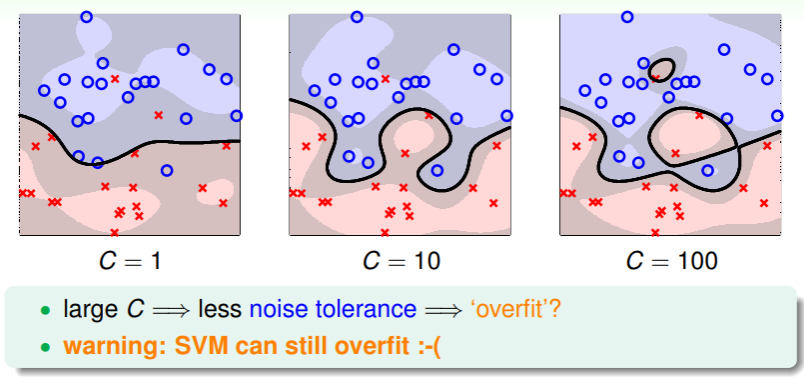
• 这表明，即使是 soft-margin SVM ，仍有过拟合的风险，因此我们要小心地考虑参数 $(\gamma ,C)$ 的抉择；

Physical Meaning of ${\alpha }_n$

从物理意义上看，参数 ${\alpha }_n$ 的具体意义又是什么？

• 
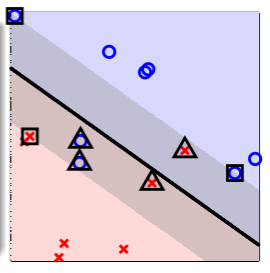
• 上图显示了一个 soft-margin SVM 与各种 SV 样本点、非 SV 样本点的分布情况，
• 非 SV 样本点，不受到 SVM 的限制，故而 ${\alpha }_n=0$ ，从而 ${\xi }_n=0$ ，
• free SV 样本点是 $0<{\alpha }_n<C$ 的那些样本，其对应的 ${\xi }_n=0$ ，即没有违反 margin 限制，它们都位于 SVM 的边界 boundary 上，
• bounded SV 样本点是 ${\alpha }_n=C$ 的那些样本，其对应的 ${\xi }_n=\text{violation margin}$ ，即在 soft-margin SVM 中违反 margin 限制的程度，它们位于边界 boundary 内部；

练习：计算 SVM 的数据集内错误率

Model Selection

我们又遇到了选择合适的模型的问题，现在以 Gaussian SVM 为例，我们考查其参数 $(C,\gamma )$ 对模型性能的影响：

• 下图横轴是参数 $C$ 的大小，纵轴是参数 $\gamma$ 的大小：
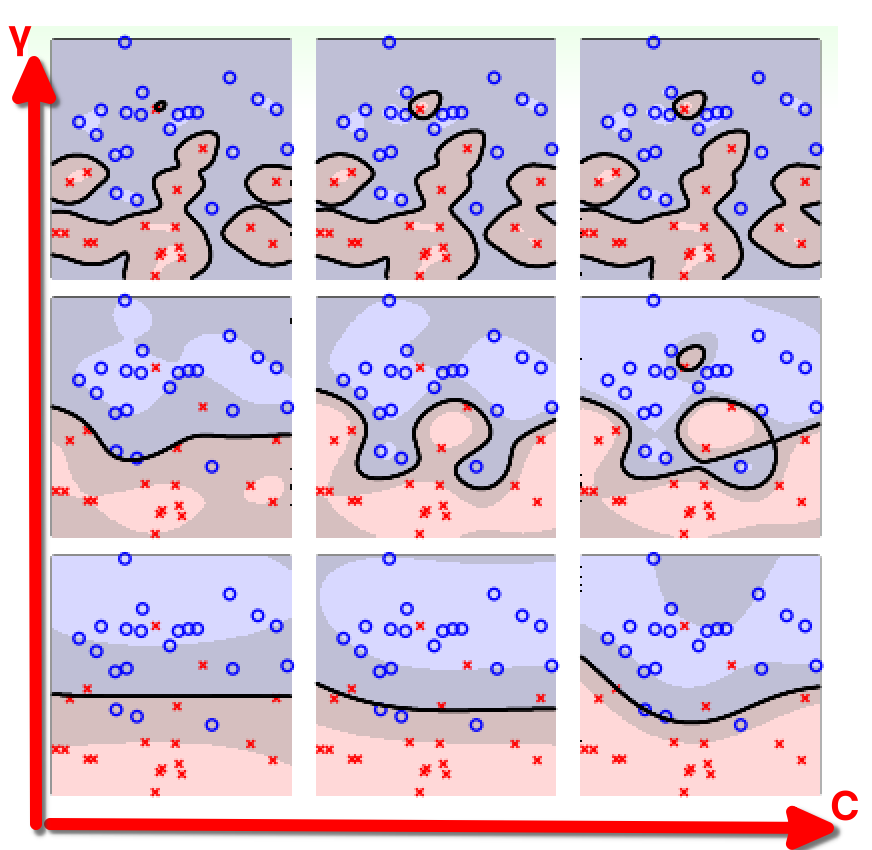
• 我们能够进行选择的依据，就是之前学习过的 交叉验证 ，不过在 SVM 中，交叉验证的犯错率 $E_{CV}(C,\gamma )$ 并不是平滑的、易求解最小值的函数，通常只能尝试不同的 $(C,\gamma )$ 的组合来试探：下图是用 V-Fold 交叉验证计算的各组合结果，则其最小者为目标模型即可

Leave-One-Out CV Bound

不过这样通过“逐个试探”的不仅效率低下，而且还容易出纰漏，因此我们有必要考查交叉验证时犯错的概率极限。回想最极端的交叉验证法—— 留一交叉验证 ：

• 如果数据集中一个样本 $({\mathbf{x}}_N,y_N)$ 在 SVM 的限制条件中最佳的 ${\alpha }_N=0$ ，即意味着它是非支撑向量，那么即是祛除该样本，剩余的 $N-1$ 个样本的 $({\alpha }_1,{\alpha }_2,...,{\alpha }_{N-1})$ 仍然是最优的（否则还可以从中取出一个 ${\alpha }_i=0$ ，去掉之后仍然最优）；
• 这意味着祛除该样本的留一交叉验证中，两个假设 $g^{-}$ 与 $g$ 没有区别，即 $e_{\text{non-SV}}=\text{err}(g^{-},\text{non-SV})=\text{err}(g,\text{non-SV})=0$ ，而对真正有用的支撑向量，其在留一交叉验证中的影响 $e_{\text{SV}}\le 1$ ；
• 因此可以得到留一交叉验证在 SVM 中的犯错率 $E_{loocv}\le \frac{\#\text{SV}}{N}$ ，即犯错率的上限不超过支撑向量的数量在所有样本中的占比（N 的实际含义其实是 V-Fold 的折数，但在留一交叉验证中 N 在数值上等于样本数）
• 这就是在数学上证明了前面所说 SVM 中只有真正的 SV 才是有用的：

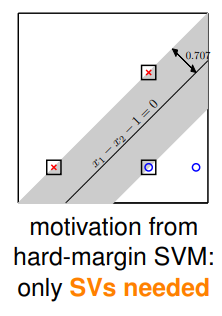
这个上界能够提供什么信息？

• 显然，支撑向量的实际数量 $\text{nSV}(C,\gamma )$ 也并不是一个平滑函数，并且在查看过所有样本点外无法完全确定；
• 另外“上界”只能用于参考，比如抛弃 SV 数量最多的那一部分 SVM 模型，但“上界”终究只是“上界”，我们不能完全依赖它作以评判：
• 因此使用 $\text{nSV}$ 作为 SVM 模型的一种安全检查是比较合理的；

练习：理解 SVM 的留一交叉验证错误率