60-Binary_Search_Tree

定义与特性

为了使二叉树支持快速查找，利用二分搜索的思路，人为的设定节点间的顺序：任一节点均不小于其左后代，也不大于其右后代

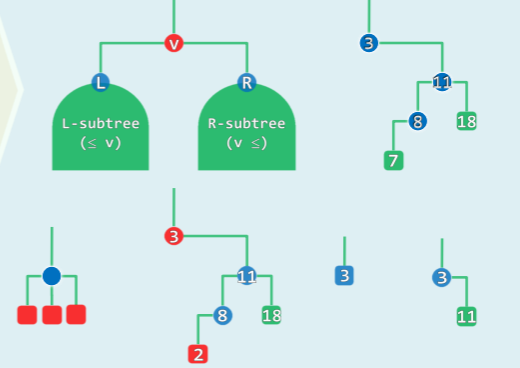
[! warning] 注意是“后代”而不是“孩子” 二叉搜索树要求的节点关系是基于左右子树，而非左右孩子。因为局部满足要求并不代表全局也满足要求。比如：

graph TD
A[3]-->B[1] & C[5]
B-->B1[0] & B2[4]
C-->C1[2] & C2[6]

此外，二叉搜索树不仅存在顺序性，而且存在单调性：

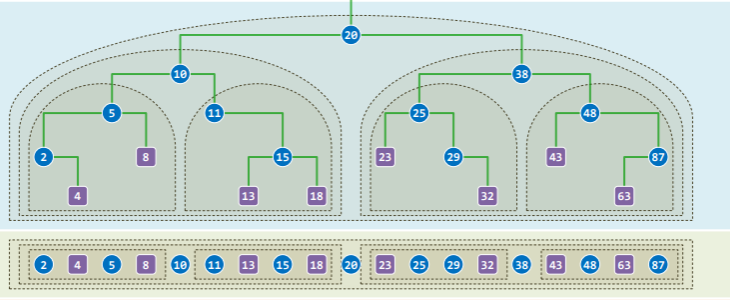
• 顺序性是对局部特征的刻画，但由此可以推出全局的单调性：
• 即，二叉搜索树在中序遍历意义下，是单调非降的。

ADT

template <typename T> class BST : public BinTree<T> {
public: //以virtual修饰，以便派生类重写
	virtual BinNodePosi<T> & search( const T & ); //查找
	virtual BinNodePosi<T> insert( const T & ); //插入
	virtual bool remove( const T & ); //删除
protected:
	BinNodePosi<T> _hot; //命中节点的父亲
	BinNodePosi<T> connect34( //3+4重构
		BinNodePosi<T>, 
		BinNodePosi<T>,
		BinNodePosi<T>,
		BinNodePosi<T>,
		BinNodePosi<T>,
		BinNodePosi<T>,
		BinNodePosi<T>); 
	BinNodePosi rotateAt( BinNodePosi ); //旋转调整
};

查找

• 从根节点出发，逐步地缩小查找范围，直到
  • 发现目标（成功），或抵达空树（失败）
• 对照中序遍历序列可见，整个过程可视作是在仿效有序向量的二分查找

template <typename T> 
BinNodePosi<T> & BST<T>::search( const T & e ) {
	if ( !_root || e == _root->data ) //空树，或恰在树根命中
	{ _hot = NULL; return _root; }
	
	for ( _hot = _root; ; ) { //否则，自顶而下
		BinNodePosi<T> & v = ( e < _hot->data ) ? _hot->lc : _hot->rc; //深入一层
		if ( !v || e == v->data ) return v; 
		_hot = v; //一旦命中或抵达叶子，随即返回
	} //返回目标节点位置的引用，以便后续插入、删除操作
} //无论命中或失败，_hot均指向v之父亲（v是根时，hot为NULL）

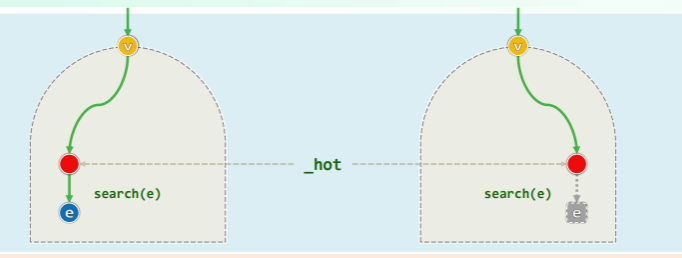上述代码的返回结果有如下两种情况：

• 查找成功时，返回一个关键码为 e 且真实存在的节点；
• 查找失败时，指向最后一次试图转向的空接点 NULL，此时不妨假想地将空节点转换为数值为 e 的哨兵节点；

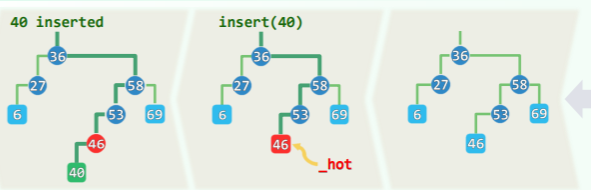
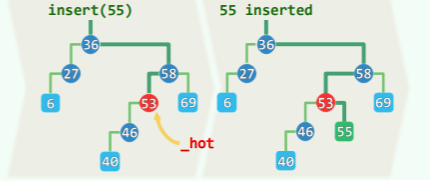
插入

借助 search()接口，可以非常快速地确定插入位置与方向：

• 若 e 已经存在，则不必操作（当然这是在讨论初期只关注各节点互异的情况，实际中没必要如此限制）
• 若 e 不存在，则将新节点作作为叶子插入：
  • _hot 作为新节点的父亲，通过 v=search (e)得到对新孩子的引用，
  • 最后令 _hot 通过 v 指向新节点。

插入操作有两种情况：

1. 插入位置低于叶节点：

   • 

2. 插入位置位于中间节点，且位置为空：

   • 

[! tip] BST 插入的元素一定是一个叶节点！

template <typename T>
BinNodePosi<T> BST<T>::insert( const T & e ) {
	BinNodePosi<T> & x = search( e ); //查找目标（留意_hot的设置）
	if ( ! x ) { //既已禁止雷同元素，故仅在查找失败时才实施插入操作
		x = new BinNode<T>( e, _hot ); //在x处创建新节点，以_hot为父亲
		_size++; 
		updateHeightAbove( x ); //更新全树规模，更新x及其历代祖先的高度
	}
	return x; //无论e是否存在于原树中，至此总有x->data == e
} //验证：对于首个节点插入之类的边界情况，均可正确处置

• 时间主要消耗于 search (e)和 updateHeightAbove (x)；
• 均线性正比于 x 的深度，不超过树高⇒O (logn)

删除

//主算法
template <typename T>
bool BST<T>::remove( const T & e ) {
	BinNodePosi<T> & x = search( e ); //定位目标节点
	if ( !x ) return false; //确认目标存在（此时_hot为x的父亲）
	removeAt( x, _hot ); _size--; //分两大类情况实施删除
	_size--; updateHeightAbove( _hot ); //更新全树规模，更新_hot及其历代祖先的高度
	return true;
} //删除成功与否，由返回值指示
//累计O(h)时间，主要消耗于search()、updateHeightAbove()、removeAt()中的succ()

// removeAt()
template <typename T>
static BinNodePosi<T> removeAt( BinNodePosi<T> & x, BinNodePosi<T> & hot ) {
	BinNodePosi<T> w = x; //实际被摘除的节点，初值同x
	BinNodePosi<T> succ = NULL; //实际被删除节点的接替者
	if ( ! HasLChild( *x ) ) succ = x = x->rc; //左子树为空
	else if ( ! HasRChild( *x ) ) succ = x = x->lc; //右子树为空
	else { //若x的左、右子树并存，则 
		w = w->succ(); 
		swap( x->data, w->data ); //令*x与其后继*w互换数据 
		BinNodePosi u = w->parent; //原问题即转化为，摘除非二度的节点
		w ( u == x ? u->rc : u->lc ) = succ = w->rc; //兼顾特殊情况：u可能就是x
	//时间主要消耗于succ()，正比于x的高度——更精确地，search()与succ()总共不过O(h)
	}
	hot = w->parent; //记录实际被删除节点的父亲
	if ( succ ) succ->parent = hot; //将被删除节点的接替者与hot相联
	release( w->data ); release( w ); return succ; //释放被摘除节点，返回接替者
} //不经过else分支的情况，情况仅需O(1)时间

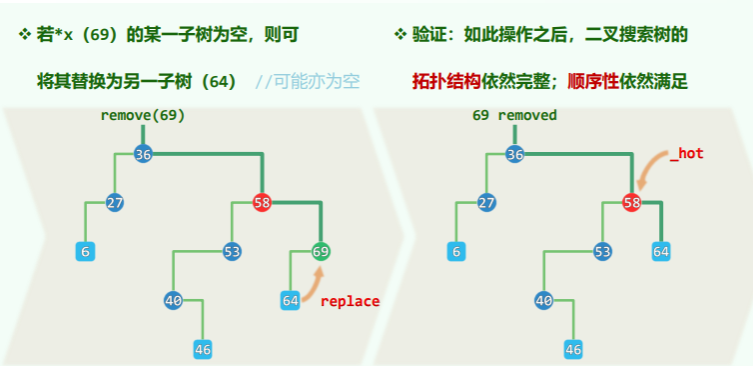
从 BST 中删除有两种情况：

1. 删除节点是其父节点的唯一孩子（分支）：

   • 

2. 删除节点有兄弟及兄弟的分支：

   • 
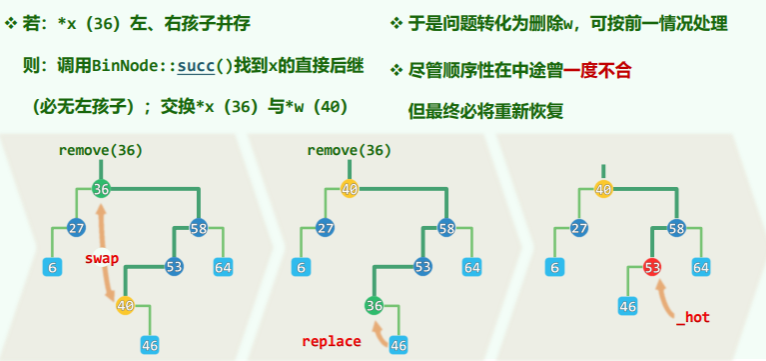
   • 思路是直接后继一定没有左孩子（有左孩子则其左孩子就成为直接后继），交换之，
   • 由此可以保证，除了直接后继及直接后继的后代，其余 BST 的部分均不受影响；
   • 此时由于直接后继转换为没有兄弟的第一类情况，直接复用第一类的思想即可。

期望树高

非常直观，BST 的所有操作都正比于树高：O (h)。因此若树高不能有效控制，就无法体现出 BST 的优势——甚至最坏情况下退化成一条链。

考虑随机生成 n 个词条并按随机排列 $\sigma =(e_{i1},e_{i2},...,e_{i3})$ 的顺序依次插入，且每种排列出现的概率相同—— $\frac{1}{n!}$，则 BST 的平均高度为 $\Theta (\log n)$。

• 
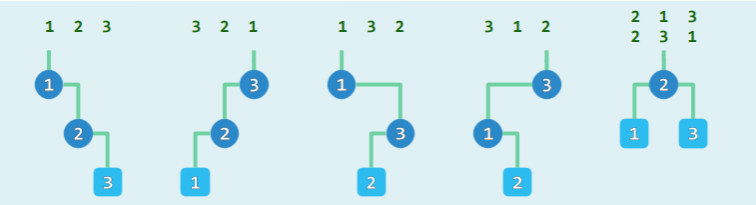
• 上图情况中，{1,2,3}序列的平均树高为 (2+2+2+2+1+1)/6 = 1.67
• 多数实际应用中的 BST 总体上都是如此生成和演化的，即便计入 remove()，也可通过随机使用 succ()和 pred()，避免逐渐倾侧的趋势——若固定使用 succ()进行删除算法，则每棵 BST 有逐渐左倾的趋势；

但若排列出现的概率不均等时，情况会有差别。考虑 n 个互异节点在遵守 BST 的顺序条件下，随机组成确定拓扑关系：

• n 个互异节点组成的 BST 的种类有 S (n)棵，其递推公式为：
• $S(n)=\sum _{k=1}^{n}S(k-1)\cdot S(n-k)=catalan(n)=\frac{(2n)!}{(n+1)!\cdot n!}$
• 同样以 {1,2,3} 序列，共五种拓扑，因此以拓扑数分析平均树高为：(2+2+2+2+1)/5 = 1.8
• 假设所有 BST 等概率出现，则平均高度为 $\Theta (\sqrt{n})$

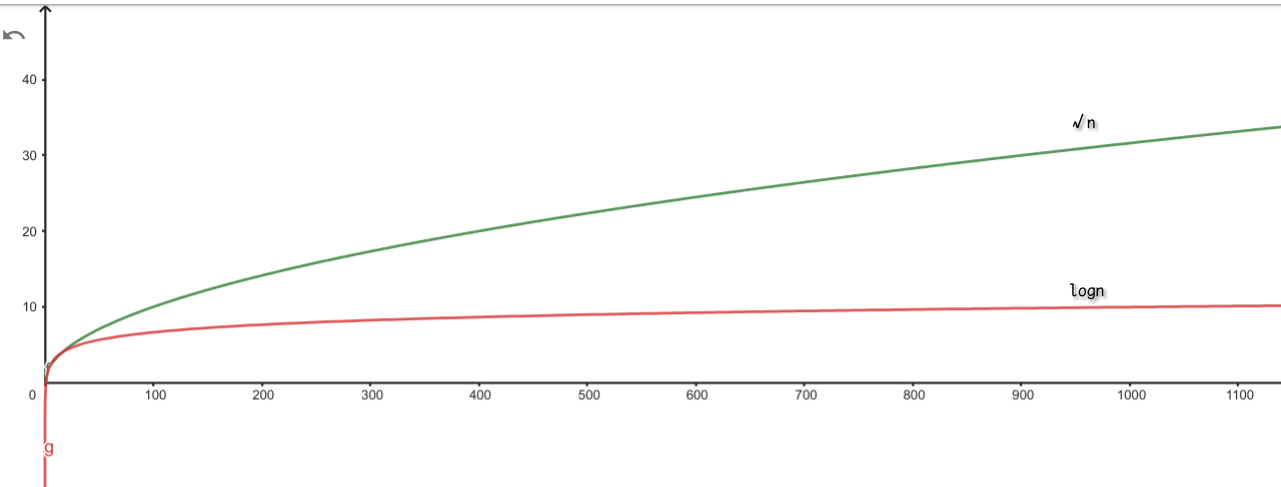
[! note] logn vs. sqrt (n) 两种口径所估计出的平均高度差异极大——谁更可信？

• 后者未免太悲观，但前者则过于乐观：BST 越低，权重越大；
• 理想随机在实际中绝难出现：局部性、关联性、（分段）单调性、（近似）周期性、…

较高甚至极高的 BST 频繁出现，不足为怪；平衡化处理很有必要！

平衡化

1. 理想平衡：

   • 节点数目固定时，兄弟子树的高度越接近（平衡），全树也将倾向于更低；
   • 由 n 个节点组成的二叉树，高度不致低于 $\lfloor {\log }_{2}n\rfloor$ ，达到这个下界时，称作理想平衡；
   • 
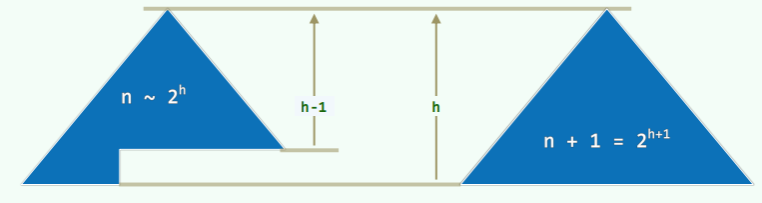
   • 大致相当于完全树甚至满树：叶节点只能出现于最底部的两层——条件过于苛刻

2. 渐进平衡：

   • 适当地放松标准——退一步海阔天空：高度渐近地不超过 O (logn)，即可接受；
   • 

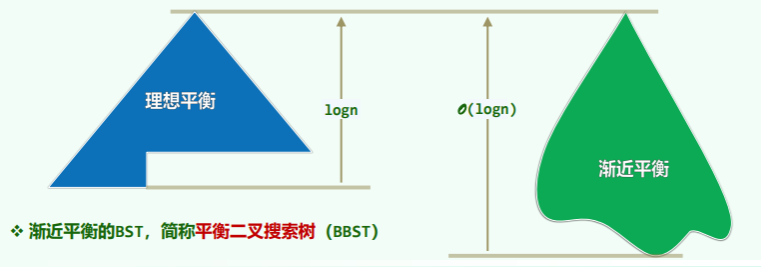
为了实现渐进平衡，我们需要确定两个原则——上下可变、左右不乱：

• 父子兄弟节点的连接关系可以改变、颠倒；
• 但中序遍历的序列不可破坏，全局仍然单调非降：
• 

BBST 是 BST 的子集，同样满足左小右大的顺序性：

• 单次动态修改后，至多 O (logn)处局部不再满足顺序性——可能修复一处上升到上一层，相继违反，不一定同时；
• 因此可以在 O (logn)时间内修复这些局部以满足 BST 的要求；
• 修复操作是通过旋转局部的父子兄弟完成：
• 
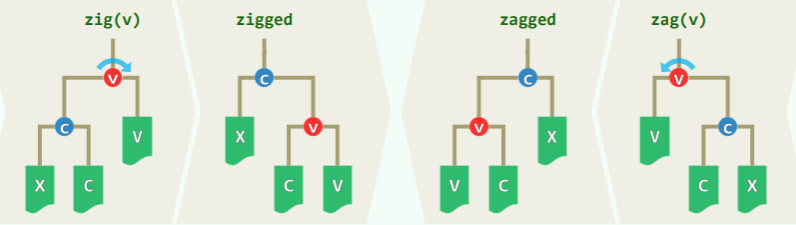
• zig 和 zag 只涉及局部的常数个节点的旋转操作，只需调整其中的连接关系；
• zig 调整之后，v 的深度加 1，c 的深度减 1；zag 正好相反；
• 子树甚至全树的高度变化幅度不会超过 1；
• 实际上不超过 O (n)次旋转，可以将任一 BST 转换为另一棵 BST；