20-Vector

ADT

方法名	描述	适用对象
size ()	报告向量当前的规模（元素总数）	向量
get (r)	获取秩为 r 的元素	向量
put (r, e)	用 e 替换秩为 r 元素的数值	向量
insert (r, e)	e 作为秩为 r 元素插入，原后继依次后移	向量
remove (r)	删除秩为 r 的元素，返回该元素原值	向量
disordered ()	判断所有元素是否已按非降序排列	向量
sort ()	调整各元素的位置，使之按非降序排列	向量
find (e)	查找目标元素 e	向量
search (e)	查找 e，返回不大于 e 且秩最大的元素	有序向量
deduplicate (), uniquify ()	剔除重复元素	向量/有序向量
traverse ()	遍历向量并统一处理所有元素	向量

动态空间管理

倍增扩容

template <typename T> void Vector<T>::expand() { 
	//向量空间不足时扩容
	if ( _size < _capacity ) return; //尚未满员时，不必扩容
	_capacity = max( _capacity, DEFAULT_CAPACITY ); //不低于最小容量
	T* oldElem = _elem; 
	_elem = new T[ _capacity <<= 1 ]; //容量加倍
	for ( Rank i = 0; i < _size; i++ ) //复制原向量内容
		_elem[i] = oldElem[i]; //T为基本类型，或已重载赋值操作符'='
	delete [] oldElem; //释放原空间
} //得益于向量的封装，尽管扩容之后数据区的物理地址有所改变，却不致出现野指针

最坏情况：在初始容量1的满向量中，连续插入 $n=2^m\gg 2$ 个元素，而无删除操作。于是，在第 1、2、4、8、16、… 次插入时，都需扩容，每次扩容中复制原向量的时间成本为 $1,2,4,8,...,2^{m-1},2^m=n$ 。

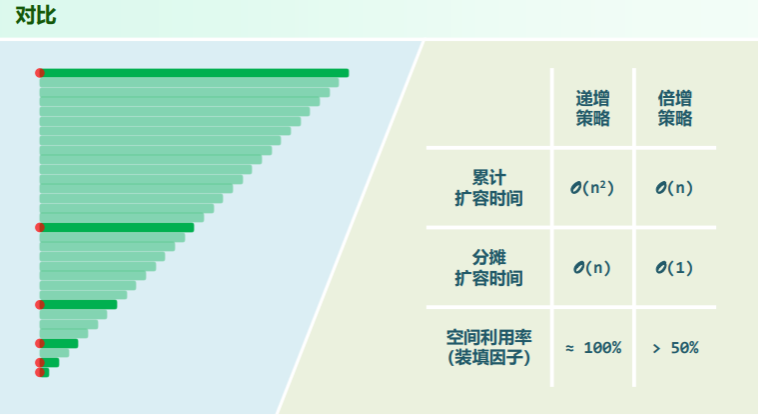
这意味着总体耗时 $O(n)$，每次插入操作的分摊成本为 $O(1)$ 。

递增扩容

即在倍增扩容策略中，将容量变化改为： _elem = new T[_capacity += INCREMENT];

考虑最坏情况：每次在向量中，连续插入 $n=m\cdot INCREMENT\gg 2$ 个元素，却并无删除操作。则会导致在第 $I+1,2I+1,3I+1,...$ 次插入时，都需要扩容，每次扩容时复制原向量的成本依次为 $I,2I,3I,...$

这是一个算术级数，总体耗时 $O(n^2)$，每次插入操作的分摊成本为 $O(n)$。

缩容

当连续删除操作后，装填因子低于某一阈值(如 25%)，称向量发生了下溢。在格外关注利用率的场合，发生下溢时有必要时当缩减内部向量的容量：

template <typename T> void Vector<T>::shrink() { 
	//装填因子过小时压缩向量所占空间
	if ( _capacity < DEFAULT_CAPACITY << 1 ) return; //不致收缩到DEFAULT_CAPACITY以下
	if ( _size << 2 > _capacity ) return; //以25%为界
	T* oldElem = _elem; 
	_elem = new T[_capacity >>= 1]; //容量减半
	for ( Rank i = 0; i < _size; i++ ) _elem[i] = oldElem[i]; //复制原向量内容
	delete[] oldElem; //释放原空间
}

平均分析 Vs. 分摊分析

平均（average complexity）：根据各种操作出现概率的分布，将对应的成本加权平均

• 各种可能的操作，作为独立事件分别考查
• 割裂了操作之间的相关性和连贯性
• 往往不能准确地评判数据结构和算法的真实性能

分摊（amortized complexity）：连续实施的足够多次操作，所需总体成本摊还至单次操作

• 从实际可行的角度，对一系列操作做整体的考量
• 更加忠实地刻画了可能出现的操作序列
• 更为精准地评判数据结构和算法的真实性能

习题集 2-1 的进一步阐述

问题：关于某个算法，甲证明“其平均时间复杂度为 O(n)”，乙证明“其分摊时间复杂度为 O(n)”。 若他们的结论均正确无误，则是甲的结论蕴含乙的结论，还是乙的结论蕴含甲的结论，还是互不蕴含？

解答： 两个结论之间不存在蕴含关系，但相对而言，后一结论更为可靠和可信。

• 所谓平均复杂度，是指在假定各种输入实例的出现符合某种概率分布之后，进而估算出的加权复杂度均值。比如在教材的第 12.1.5 节中，将基于“待排序的元素服从独立均匀随机分布”这一假设，估算出快速排序算法在各种情况下的加权平均复杂度。
• 所谓分摊复杂度，则是纵观连续的足够多次操作，并将其间总体所需的运行时间分摊至各次操作。与平均复杂度的本质不同在于，这里强调，操作序列必须是的确能够真实发生的，其中各次操作之间应存在前后连贯的时序关系。比如在参考文献¹中，Tarjan 采用势能分析法对伸展树所有可能的插入、删除操作序列进行分析，并估算出在此意义下单次操作的分摊执行时间。

由此可见，前者不必考查加权平均的各种情况出现的次序，甚至其针对概率分布所做的假设未必符合真实情况；后者不再割裂同一算法或数据结构的各次操作之间的因果关系，更加关注其整体的性能。综合而言，基于后一尺度得出的分析结论，应该更符合于真实情况，也更为可信。

以教材2.4节中基于容量加倍策略的可扩充向量为例。若采用平均分析，则很可能因为所做的概率分布假定与实际不符，而导致不准确的结论。比如若采用通常的均匀分布假设，认为扩容与不扩容事件的概率各半，则会得出该策略效率极低的错误结论。实际上，只要假定这两类事件出现的概率各为常数，就必然导致这种误判。而实际情况是，采用加倍扩容策略后，在其生命期内随着该数据结构的容量不断增加，扩容事件出现的概率将以几何级数的速度迅速趋近于零。对于此类算法和数据结构，唯有借助分摊分析，方能对其性能做出综合的客观评价。

无序向量

插入、删除、查找

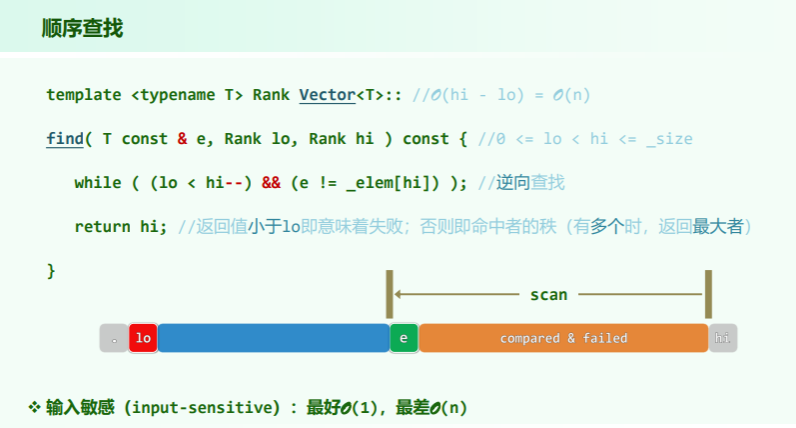
去重

注意无序向量的去重，需要对每一个元素都遍历一遍，因此时间复杂度为 $O(n^2)$；而若排序后去重，则只需 $O(n\log n+n)$ （注意懒删除策略）

遍历（函数对象版）

对向量中的每一元素，统一实施 visit() 操作 //如何指定 visit()？如何将其传递到向量内部？

template <typename T> template <typename VST> //函数对象，全局性修改更便捷
void Vector<T>::traverse( VST & visit )
{ for ( Rank i = 0; i < _size; i++ ) visit( _elem[i] ); }

举例：

比如，为统一地将向量中所有元素分别加一，只需：

• 实现一个可使单个 T 类型元素加一的类（结构）

template <typename T> //假设T可直接递增或已重载操作符“++”
struct Increase //函数对象：通过重载操作符“()”实现
{ virtual void operator()( T & e ) { e++; } }; //加一

• 将其作为参数传递给遍历算法

template <typename T> void increase( Vector<T> & V )
{ V.traverse( Increase<T>() ); } //即可以之作为基本操作，遍历向量

有序向量

二分查找 a

有序向量中，每个元素都是轴点，以任一元素 x = S[mi] 为界，都可将待查找区间 [lo,hi) 分为三部分：$S[lo,mi)\le S[mi]\le S(mi,hi)$

因此只需要将目标元素 e 与 x 做一次比较，即可分三种情况进一步处理：

• e < x：则 e 若存在必属于左侧子区间，故可（减除 S[mi,hi) 并）递归深入 S[lo, mi)
• x < e：则 e 若存在必属于右侧子区间，亦可（减除 S[lo,mi] 并）递归深入 S(mi, hi)
• e = x：已在此处命中，可随即返回

若取轴点 mi 作中点，则每经过至多两次比较，要么命中，要么将问题规模缩减一半：

线性递归：$T(n)=T(\frac{n}{2})+O(1)=O(\log n)$，每次取轴点都是中点，因此递归深度是 $O(\log n)$，每个递归实例耗时 $O(1)$ 。

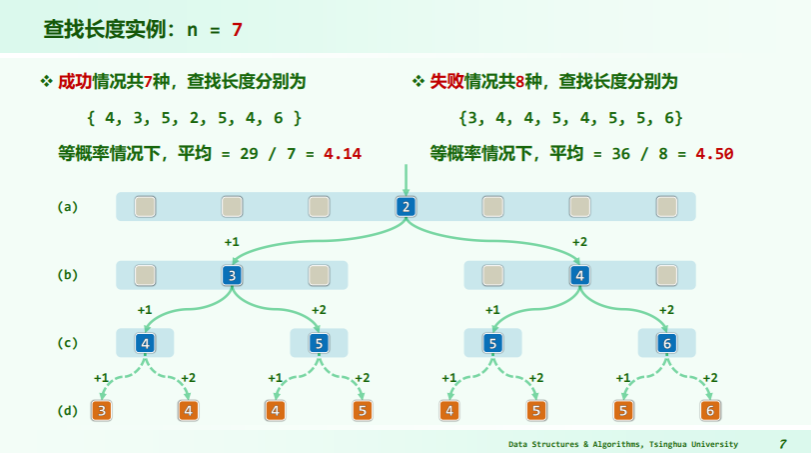
查找长度：关键码比较的次数

• 成功、失败时查找长度为 $O(1.50\cdot \log n)$

Fibonacci 查找

binSearch 的版本 A 中，转向左、右分支前的关键码比较次数不等，而递归深度却相同，若通过递归深度的不均衡对转向成本的不均衡做补偿，平均查找长度应能进一步缩短！

比如，若有 $n=fib(k)-1$，则可取 $mi=fib(k-1)-1$，于是前后子向量长度分别为 $fib(k-1)-1,fib(k-2)-1$ ：

template <typename T> //0 <= lo <= hi <= _size
static Rank fibSearch( T * S, T const & e, Rank lo, Rank hi ) {
	for ( Fib fib(hi - lo); lo < hi; ) { //Fib数列制表备查
		while ( hi - lo < fib.get() ) fib.prev(); //自后向前顺序查找轴点（分摊O(1)）
		Rank mi = lo + fib.get() - 1; //确定形如Fib(k)-1的轴点
		if ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)
		else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)
		else return mi; //命中
	}
	return -1; //失败
} //有多个命中元素时，不能保证返回秩最大者；失败时，简单地返回-1，而不能指示失败的位置

平均查找长度：常系数略优

• 二分查找的轴点取自 $\lambda =0.5$ 处，fibSearch 的轴点取自 $\lambda =0.618$ 处（因为 Fib 数列的后项与前项比值极限为 0.618）

二分查找 b

binSearch-A 中的转向分支有三个，因此导致不平衡，B 方案直接解决该问题——所有分支只有两个方向：

• 取 mi 作轴点不变，但是 e<x 时深入左侧 [lo, mi)
• x<=e 时深入右侧 [mi,hi)，直到 hi-lo=1 时才能判断是否命中

最坏情况比 A 更坏，但总体性能均衡。

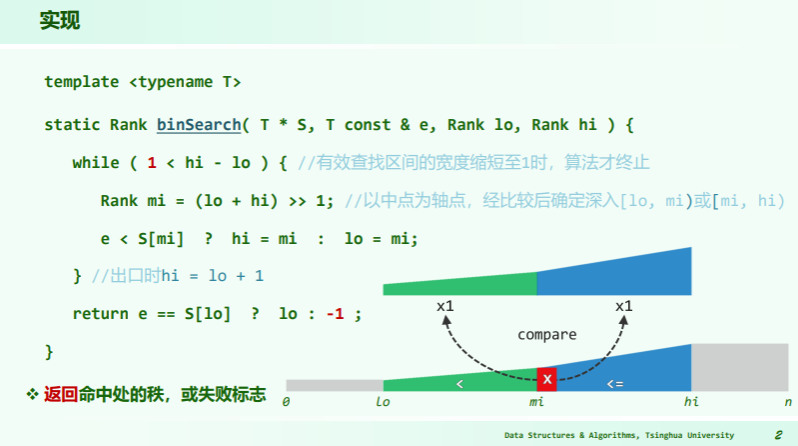
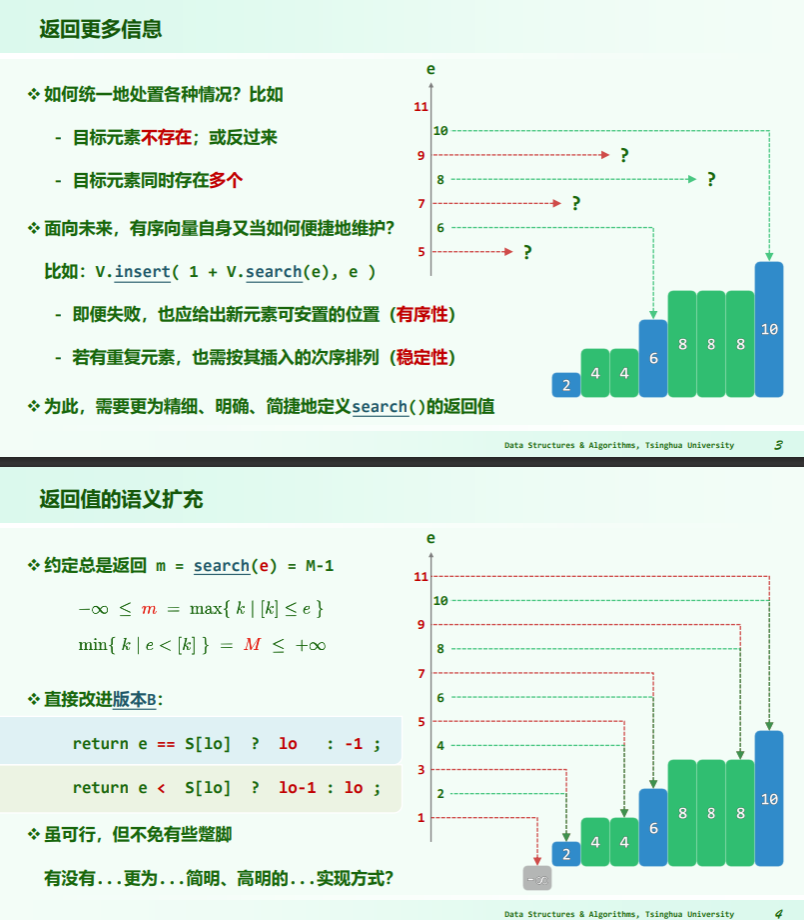
二分查找 c

template <typename T>
static Rank binSearch( T * S, T const & e, Rank lo, Rank hi ) {
	while ( lo < hi ) { //不变性：A[0, lo) <= e < A[hi, n)
		Rank mi = (lo + hi) >> 1;
		e < S[mi] ? hi = mi : lo = mi + 1; 
	} //出口时，区间宽度缩短至0，且必有S[lo = hi] = M
	return lo - 1; //至此，[lo]为大于e的最小者，故[lo-1] = m即为不大于e的最大者
} //留意与版本B的差异
//无论成功与否，返回的秩必然会严格地符合接口的语义约定...

版本 C 与 B 的三点差异：

1. 查找区间宽度缩短至 0 时算法结束(而不是 1)，此时 lo=hi 且指向大于 e 的最小者；
2. 转入右侧子向量时，左边界取 mi+1 而非 mi，
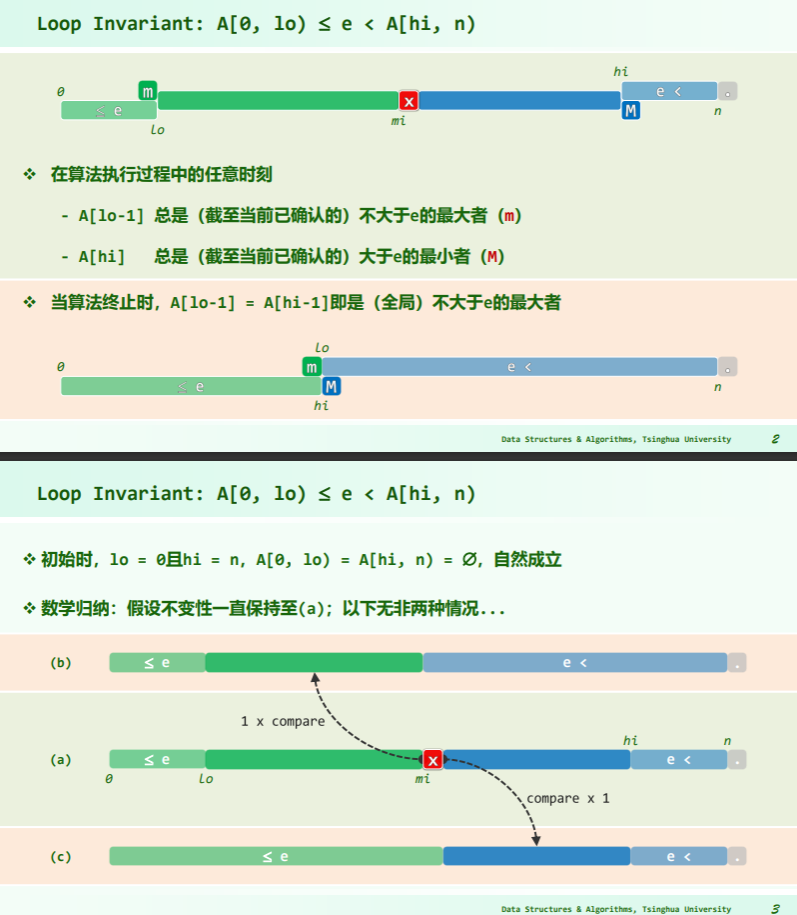
   • 会造成 A[mi] 遗漏吗？——不会，因为若正好取到 A[mi]，则在算法结束后会处于大于 A[mi] 的最小值的最小秩处，-1 即可解决问题；（考虑到有序向量中的重复元素）
   • 数学归纳证明：版本 C 中的循环体，具有如下不变性： A[0, lo) 中的元素皆不大于 e；A[hi, n) 中的元素皆大于 e
   • 首次迭代时，lo = 0 且 hi = n， A[0, lo) 和 A[hi, n) 均空，不变性自然成立。
   • 
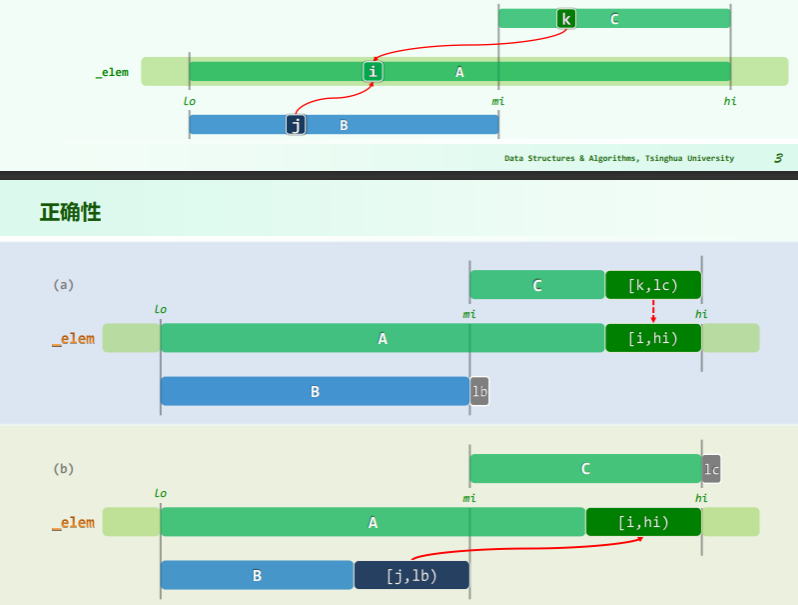
   • 如图所示，设在某次进入循环时以上不变性成立，以下无非两种情况。
     • 若 e < A[mi]， 则如图 (b)，在令 hi = mi 并使 A[hi, n) 向左扩展之后，该区间内的元素皆不小于 A[mi]，当然也仍然大于 e。
     • 反之，若 A[mi] <= e，则如图 (c)，在令 lo = mi + 1 并使 A[0, lo) 向右拓展之后，该区间内的元素皆不大于 A[mi]，当然也仍然不大于 e。总之，上述不变性必然得以延续。
3. 循环终止时，lo = hi
   • 考查此时的元素 A[lo - 1] 和 A[lo]：作为 A[0, lo) 内的最后一个元素，A[lo - 1] 必不大于 e；
   • 作为 A[lo, n) = A[hi, n) 内的第一个元素，A[lo] 必大于 e。也就是说，A[lo - 1] 即是原向量中不大于 e 的最后一个元素。
   • 因此在循环结束之后，无论成功与否，只需返回 lo - 1 即可

习题 2-16 对不同极端情况的接口规范分析

• [lo, hi) 中的元素均 < e；
• [lo, hi) 中的元素均 = e；
• [lo, hi) 中的元素均 > e；
• [lo, hi) 中既包含 < e 的元素，也包含 > e 的元素，但不含 = e 的元素。

插值查找

大数定律：越长的序列，元素分布越有规律。

若假定序列的分布为独立、均匀的随机分布，则 [lo,hi] 内各元素大致以线性趋势增长：

$$\frac{mi-lo}{hi-lo}\approx \frac{e-A[lo]}{A[hi]-A[lo]}$$

因此可猜测轴点为：

$$mi\approx lo+(hi-lo)\cdot \frac{e-A[lo]}{A[hi]-A[lo]}$$

冒泡排序

基本

template <typename T> void Vector<T>::bubbleSort( Rank lo, Rank hi ) {
	while ( lo < --hi ) //逐趟起泡扫描
		for ( Rank i = lo; i < hi; i++ ) //逐对检查相邻元素
			if ( _elem[i] > _elem[i + 1] ) //若逆序
				swap( _elem[i], _elem[i + 1] ); //则交换
}
 

• Loop Invariant：经 k 趟扫描交换后，最大的 k 个元素必然就位
• Convergence：经 k 趟扫描交换后，问题规模缩减至 n-k
• Correctness：经至多 n 趟扫描后，算法必然终止，且能给出正确解答

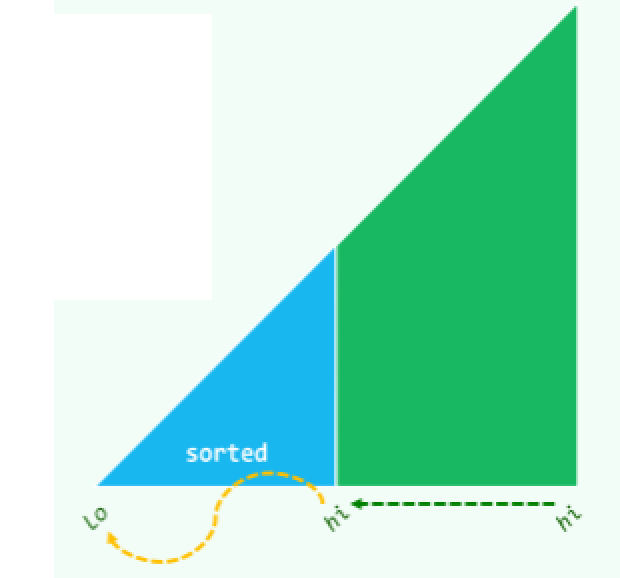
提前终止

[hi] 就位后，[lo,hi) 可能已经有序（sorted）——此时，应该可以跳过这段：

template <typename T> void Vector<T>::bubbleSort( Rank lo, Rank hi ) {
	for ( bool sorted = false; sorted = !sorted; hi-- )
		for ( Rank i = lo + 1; i < hi; i++ )
			if ( _elem[i-1] > _elem[i] )
				swap( _elem[i-1], _elem[i] ), sorted = false;
}

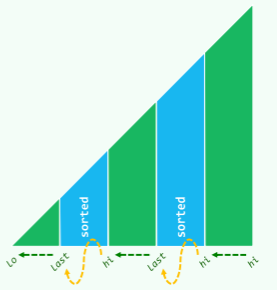
跳跃

在排序过程中，可能某一后缀 [last,hi] 已经有序，此时可以跳过它们：

template <typename T> void Vector<T>::bubbleSort( Rank lo, Rank hi ) {
	for ( Rank last; lo < hi; hi = last )
		for ( Rank i = (last = lo) + 1; i < hi; i++ )
			if ( _elem[i-1] > _elem[i] )
				swap( _elem[i-1], _elem[last = i] );
}

综合评价

• 时间效率：最好 $O(n)$，最坏 $O(n^2)$
• 起泡排序算法是稳定的，因为在起泡排序中，唯有相邻元素才可交换
• 在 if 一句的判断条件中，若把 > 换成 >=，将有何变化？——变不稳定

归并排序

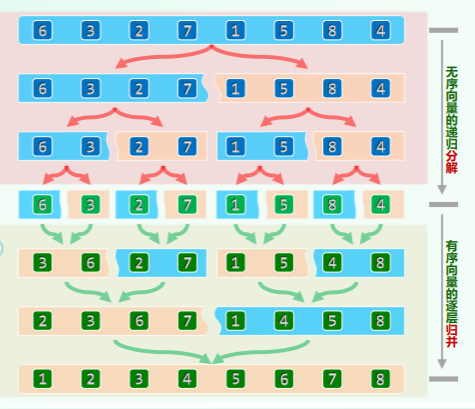
// 分治
template <typename T> void Vector<T>::mergeSort( Rank lo, Rank hi ) {
	if ( hi - lo < 2 ) return; //单元素区间自然有序，否则...
	Rank mi = (lo + hi) >> 1; //以中点为界
	mergeSort( lo, mi ); //对前半段排序
	mergeSort( mi, hi ); //对后半段排序
	merge( lo, mi, hi ); //归并(核心操作，请看下文)
}

递推方程：$T(n)=2T(\frac{n}{2})+O(n)$

2-way merge

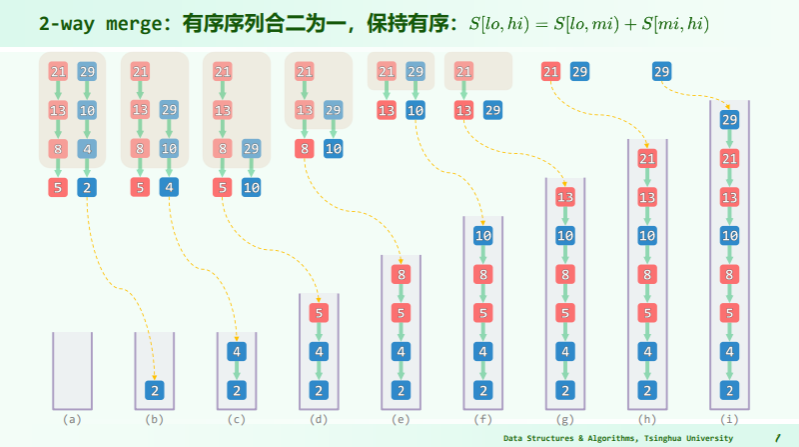
template <typename T> //[lo, mi)和[mi, hi)各自有序
void Vector<T>::merge( Rank lo, Rank mi, Rank hi ) { //lo < mi < hi
	Rank i = 0;
	T* A = _elem + lo; //A = _elem[lo, hi)
	
	Rank j = 0, lb = mi - lo;
	T* B = new T[lb]; //B[0, lb) <-- _elem[lo, mi)
	for ( Rank i = 0; i < lb; i++ ) B[i] = A[i]; //复制出A的前缀
	Rank k = 0, lc = hi - mi; T* C = _elem + mi;
	//后缀C[0, lc] = _elem[mi, hi)，就地
	
	while ( ( j < lb ) && ( k < lc ) ) //反复地比较B、C的首元素
		A[i++] = ( B[j] <= C[k] ) ? B[j++] : C[k++]; //小者优先归入A中
	while ( j < lb ) //若C先耗尽，则
		A[i++] = B[j++]; //将B残余的后缀归入A中——若B先耗尽呢？
	delete[] B; //new和delete非常耗时，如何减少？
}

• 开辟存放 B 的空间需要 $O(n)$；
• B 先耗尽会发生什么？如果在合并的过程中，左侧子向量 [lo, mi) 的元素（由数组 B 表示）先被耗尽，而右侧子向量 [mi, hi) 的元素还有剩余，那么合并操作将继续将右侧子向量的剩余元素复制到合并后的子向量 A 的末尾。这不会导致问题，因为右侧子向量的剩余部分本身就已经有序（根据归并排序的性质），所以它们可以直接添加到合并后的子向量的末尾，不会影响排序的正确性。
• 如何减少 new 和 delete 的时间？ ^b86745
  • 使用内存池： 可以实现一个内存池来管理和重复利用已分配的内存块，而不是频繁地调用 new 和 delete。这可以显著减少内存分配和释放的时间开销。
  • 使用栈内存： 对于较小的数组或数据结构，可以考虑使用栈内存而不是动态分配内存。这将减少 new 和 delete 的使用，因为栈内存的分配和释放通常更快。
  • 合并操作优化： 可以尝试优化合并操作，减少对动态数组的依赖。例如，可以在合并操作中传递一个额外的缓冲区参数，避免动态分配内存，或者将合并操作与其他操作结合，以减少内存分配的次数。
  • 使用标准库容器： 最好的方法可能是使用标准库中提供的容器和算法，它们已经经过高度优化，可以减少内存分配和释放的开销。

时间复杂度

二路归并中，两个 while 循环每迭代一步 i 都会递增；j 或 k 中之一也会随之递增

• 因：0 <= j <= lb, 0 <= k <= lc
• 故： 累计迭代步数 0<= lb + lc = n 二路归并只需 $O(n)$ 时间 （注意，即便 lb 和 lc 不相等，甚至相差悬殊，这一结论依然成立）
• 于是可知，归并排序的时间复杂度为 $O(n\log n)$

优缺点分析与改进

优点: call-by-rank, stable, extensible, parallel

• 实现最坏情况下最优 $O(n\log n)$ 性能的第一个排序算法
• 不需随机读写，完全顺序访问——尤其适用于列表之类的序列、磁带之类的设备
• 只要实现恰当，可保证稳定——出现雷同元素时，左侧子向量优先
• 可扩展性极佳，十分适宜于外部排序——海量网页搜索结果的归并
• 易于并行化 缺点
• 非就地，需要对等规模的辅助空间——可否更加节省？
  • 原地归并 ——以时间换空间
  • 习题 2-27：改进 mergeSort ()适应于大致有序情况
• 即便输入已是完全（或接近）有序，仍需 $\Omega (n\log n)$ 时间——如何改进？
  • 在归并排序的 merge 过程中, 检查当前两个子数组是否已有序。如果是, 直接合并两个子数组, 不进行比较和交换操作。
  • 另外, 可以在递归分割数组前, 检查整个数组是否已基本有序。如果是, 直接退出递归, 不再继续分割。
  • 可以先对数组进行一次快速排序的 partition 操作, 以检测数组是否基本有序。如果 partition 后的切分点偏移很小, 说明原数组已近乎有序, 可以直接插入排序。
  • 对近乎有序的数组, 也可以先进行一次简单的冒泡排序, 如果没有交换就说明已有序, 避免再做复杂的归并排序。

1. 自然归并排序（Natural Merge Sort）： 这是一种针对已经有序或部分有序输入的改进版本。它会识别已经有序的子序列，并在合并时跳过这些子序列，从而减少比较和交换的次数。这可以显著提高性能，特别是对于接近有序的输入。

2. 插入排序的改进： 可以使用插入排序来处理小规模子问题，而不是继续划分和递归。对于小规模子问题，插入排序通常比归并排序更快。这可以减少对于已经有序部分的排序时间。

3. 三路归并排序： 传统的归并排序是两路归并，即将数组分成两个子问题。三路归并将数组分成三个子问题，可以更好地处理已经有序的输入。但需要注意，三路归并的实现相对复杂一些。

4. 自适应排序： 一些排序算法，如Timsort，具有自适应性，它们可以根据输入的特性选择不同的排序策略。对于部分有序的输入，它们可能会选择更快的排序方法。

习题：21-Vector-Exercise

Footnotes

1. Sleator D D, Tarjan R E. Self-adjusting binary trees[C]//Proceedings of the fifteenth annual ACM symposium on Theory of computing. 1983: 235-245. ↩