90-Linear-Regression

Linear Regression Problem

回顾一下什么是 Regression ？现在我们以银行批准申请借贷额度的问题为例介绍 Linear Regression：

• 首先，这个问题里的输出与姊妹问题——信用卡批准与否——不一样，而是属于实数集，作为“额度”—— $\mathcal{Y}=\mathbb{R}$ ；
• 我们对线性回归的假设 $h(\mathbf{x})$ 可以这样用数学的语言描述：对于一个用户的特征向量 $\mathbf{x}=(x_0,x_1,x_2,...,x_d)$，我们对每个维度分配各自的权重，然后计算特征向量与权重向量的内积 $h(\mathbf{x})=\sum _{i=0}^d{w}_i{x}_i={\mathbf{w}}^T\mathbf{x}$ ，与姊妹问题不同的是不再使用 sign 函数和 threshold 进行二元分类；

Illustration of Linear Regression

用图形直观地表示线性回归：

• 
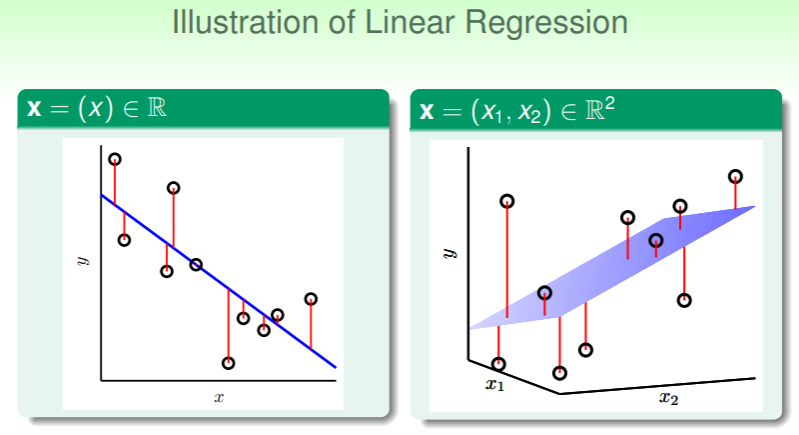
• 在一维特征向量（忽略 $w_0$，它没有实际意义）的问题里，得到的假设 $h(\mathbf{x})$ 是一个直线，二维向量则是平面，更高维的向量我们称为超平面（hyperplane）；
• 样本点 $(\mathbf{x},y)$ 的实际观察值 y 与假设 $h(\mathbf{x})$ 算出的估计值之差，称为残差（residual），线性回归的目标就是找到能够满足残差和最小的假设；

Error Evaluation

线性回归问题中的错误估计通常使用平方法：$\text{err}(\hat{y},y)=(\hat{y}-y{)}^2$

• $E_{in}(\mathbf{w})=\frac{1}{N}\sum _{n=1}^N(h({\mathbf{x}}_n)-y_n{)}^2$
• $E_{out}(\mathbf{w})=\underset{(\mathbf{x},y)\sim P}{\mathbb{E}}({\mathbf{w}}^T\mathbf{x}-y{)}^2$

Linear Regression Algorithm

Minimize $E_{in}$

我们可以将线性回归问题中的 $E_{in}(\mathbf{w})$ 写成矩阵形式：

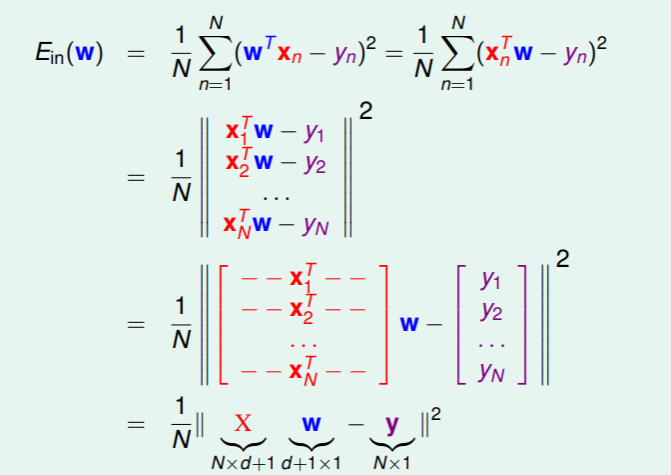• $E_{in}(\mathbf{w})$ 是连续的、可微的、凸的关于 $\mathbf{w}$ 的函数，函数图形大致如下：
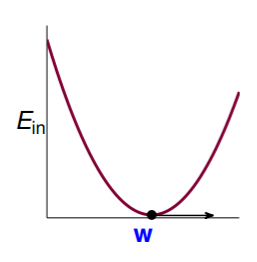• 因此要找到最佳的 ${\mathbf{w}}_{LIN}$ 使得 $E_{in}(\mathbf{w})$ 取到最小，即找到极小值点：$\nabla E_{in}(\mathbf{w})\equiv \left[\begin{array}{c}\frac{\partial E_{in}}{\partial w_0}(\mathbf{w})\\ \frac{\partial E_{in}}{\partial w_1}(\mathbf{w})\\ ...\\ \frac{\partial E_{in}}{\partial w_d}(\mathbf{w})\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ...\\ 0\end{array}\right]$ ，要找到函数的极小值点，即取梯度，我们先将其展开：
• $E_{in}(\mathbf{w})=\frac{1}{N}||\mathrm{X}\mathbf{w}-\mathbf{y}|{|}^2=\frac{1}{\mathrm{N}}\left({\mathbf{w}}^{\mathrm{T}}{\mathrm{X}}^{\mathrm{T}}\mathrm{X}\mathbf{w}-2{\mathbf{w}}^{\mathrm{T}}{\mathrm{X}}^{\mathrm{T}}\mathbf{y}+{\mathbf{y}}^{\mathrm{T}}\mathbf{y}\right)=\frac{1}{\mathrm{N}}\left({\mathbf{w}}^{\mathrm{T}}\mathrm{A}\mathbf{w}-2{\mathbf{w}}^{\mathrm{T}}\mathbf{b}+\mathrm{c}\right)$，计算这个向量函数的梯度比较麻烦，我们直接看以下推导：
• 然后找到 ${\mathbf{w}}_{LIN}$ 满足 $\frac{2}{N}({\mathrm{X}}^{\mathrm{T}}\mathrm{X}\mathbf{w}-{\mathrm{X}}^{\mathrm{T}}\mathbf{y})=\nabla {\mathrm{E}}_{\mathrm{in}}(\mathbf{w})=0$ ，
  • 如果 ${\mathrm{X}}^{\mathrm{T}}\mathrm{X}$ 可逆，那么这个解是唯一的：${\mathbf{w}}_{LIN}=({\mathrm{X}}^{\mathrm{T}}\mathrm{X}{)}^{-1}{\mathrm{X}}^{\mathrm{T}}\mathbf{y}$
    • 这种情况比较常见，因为 $N\gg d+1$ ；
  • 如果 ${\mathrm{X}}^{\mathrm{T}}\mathrm{X}$ 不可逆，那么运算平台（如 Matlab 或 Python 中使用的机器学习框架等）会给出一系列最优的近似解，记作 ${\mathbf{w}}_{LIN}={\mathrm{X}}^{†}\mathbf{y}$ ，其中 ${\mathrm{X}}^{†}=({\mathrm{X}}^{\mathrm{T}}\mathrm{X}{)}^{-1}{\mathrm{X}}^{\mathrm{T}}$ 称为 pseudo-inverse（伪逆矩阵），
    • 这种情况虽然比较少见，但若是统一使用实现良好的 ${\mathrm{X}}^{†}$ 代替，则可以在绝大多数情况下保证计算的稳定 ；

Linear Regression Flow

因此，综合起来，线性回归算法的整体流程如下：

1. 从训练集 $\mathcal{D}$，构建输入样本矩阵 $\mathrm{X}={\left[\begin{array}{c}{\mathbf{x}}_1^T\\ {\mathbf{x}}_2^T\\ ...\\ {\mathbf{x}}_N^T\end{array}\right]}_{\mathrm{N}\times (\mathrm{d}+1)}$ 和输出向量 $\mathbf{y}={\left[\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_N\end{array}\right]}_{N\times 1}$ ，
2. 计算伪逆矩阵 ${\mathrm{X}}^{†}=({\mathrm{X}}^{\mathrm{T}}\mathrm{X}{)}^{-1}{\mathrm{X}}^{\mathrm{T}}$ ，该矩阵的规格是 $(d+1)$ 行 $N$ 列 ，
3. 返回 ${\mathbf{w}}_{LIN}={\mathrm{X}}^{†}\mathbf{y}$ ；

练习：计算预测矩阵

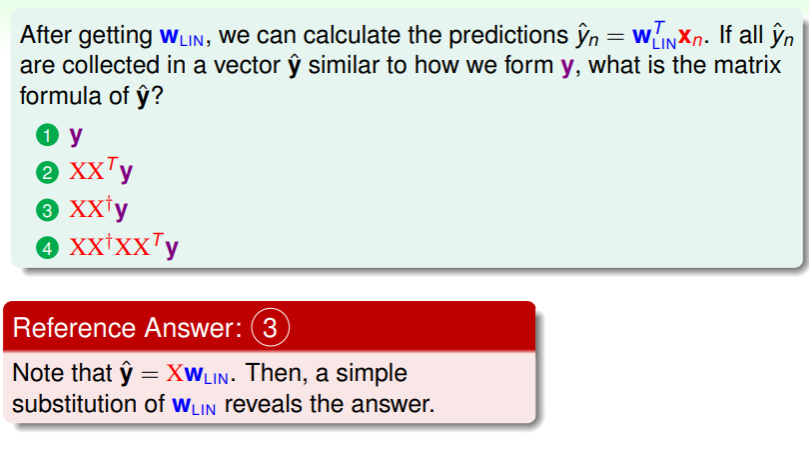
Generalization Issue

不过看起来线性规约算法并没有机器学习算法的一般特征？诸如给出接近的解、迭代式地学习并改进 $E_{in}$ ？但事实上，这只是因为这个算法过于简单、并且研究多年、理论深刻，事实上其中矩阵的每一维运算就是一次迭代，我们能够从矩阵的运算中得到最优的 $E_{in}$，并且有限的 $d_{VC}$ 保证 $E_{out}\approx E_{in}$ 。

Proof of Learning

因此，如果 $E_{out}({\mathbf{w}}_{LIN})$ 足够小，那么我们可以认为 learning 确实实现了，论证如下:

首先，展开错误评估中的平方项，可以得到：

$$E_{in}({\mathbf{w}}_{LIN})=\frac{1}{N}||\mathbf{y}-\underset{\text{predictions}}{\underbrace{\hat{\mathbf{y}}}}|{|}^2=\frac{1}{N}||\mathbf{y}-\mathrm{X}\underset{{\mathbf{w}}_{\mathrm{LIN}}}{\underbrace{{\mathrm{X}}^{†}\mathbf{y}}}|{|}^2=\frac{1}{\mathrm{N}}||(\underset{\mathrm{identity}}{\underbrace{\mathrm{I}}}-\mathrm{X}{\mathrm{X}}^{†})\mathbf{y}|{|}^2$$

，这里我们将 $\mathrm{X}{\mathrm{X}}^{†}$ 称为 Hat Matrix，记作 $\mathrm{H}$ ，它的作用是将 $\mathbf{y}$ 变为 $\hat{\mathbf{y}}$ 。（这里 $\mathrm{I}$ 矩阵其实就是单位矩阵，不过国内教科书里通常记作 $\mathrm{E}$ ，但在国外教科书里都记作 $\mathrm{I}$ ，因为 identity 这个名称的含义就是“单位”）

从几何视角来看 Hat Matrix ，对于 N 维空间 ${\mathbb{R}}^N$ ，样本的实际值向量 $\mathbf{y}$ 是这个空间中的一个 N 维向量，

• 
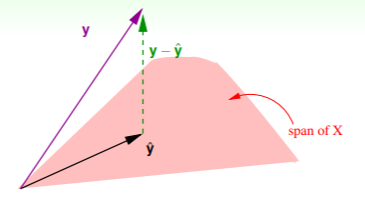
• 预测向量的计算为 $\hat{\mathbf{y}}=\mathrm{X}{\mathbf{w}}_{LIN}$ ，在线性回归算法运行之前，${\mathbf{w}}_{LIN}$ 可能是任何一个值，而 $\mathrm{X}\mathbf{w}$ 的意义是对输入矩阵 $\mathrm{X}$ 的所有列分别乘一个特定权值，从而得到由 $\mathrm{X}$ 的列向量组成的一种线性组合，因此 $\hat{\mathbf{y}}$ 必然属于 $\mathrm{X}$ 的列向量空间；（这在线性代数中称为 span of $\mathrm{X}$ columns ）
• 线性回归的目标是使得 $\mathbf{y}-\hat{\mathbf{y}}$ 尽可能小，即使得 $\hat{\mathbf{y}}$ 是空间中向量 $\mathbf{y}$ 在输入样本这一局部 $\mathrm{X}$ 上的投影 ；
• 因此 $\mathrm{H}$ 的作用就是将任何一个向量 $\mathbf{y}$ 转换成其在输入空间 $\mathbf{X}$ 上的投影，而 $\mathrm{I}-\mathrm{H}$ 的作用就是将 $\mathbf{y}$ 转换成 $\mathbf{y}-\hat{\mathbf{y}}$ ；
• 矩阵 $\mathrm{I}-\mathrm{H}$ 的迹恰好满足：$\text{trace}(\mathrm{I}-\mathrm{H})=\mathrm{N}-(\mathrm{d}+1)$，这一特点的物理意义是将 N 维空间的向量投影到 d+1 维空间，其残差的维数最多不超过 $N-(d+1)$ ；

因此，要证明 $E_{out}({\mathbf{w}}_{LIN})$ 足够小，我们在考虑输入样本中有噪音的情况下，

• 作图示应为
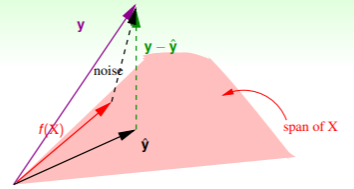
• 即如果确实存在某个理想的目标函数 $f(\mathrm{X})$，它必然属于 $\mathrm{X}$ 展开的空间，其与噪音相加就会得到 N 维空间的向量 $\mathbf{y}$ ；
• 计算 $E_{in}$ 时我们考虑的是 $\mathbf{y}-\hat{\mathbf{y}}$ ，如果对噪音同样地使用 $\mathrm{I}-\mathrm{H}$ 矩阵作残差转换，也可以得到 $\mathbf{y}-\hat{\mathbf{y}}$，即 $E_{in}({\mathbf{w}}_{LIN})=\frac{1}{N}||\mathbf{y}-\hat{\mathbf{y}}|{|}^2=\frac{1}{N}||(\mathrm{I}-\mathrm{H})\mathbf{noise}|{|}^2=\frac{1}{\mathrm{N}}(\mathrm{N}-(\mathrm{d}+1))||\mathbf{noise}|{|}^2$
• 因此如果对噪音进行平均，我们就能得到 $\overline{E_{in}}=\mathbf{noise}\text{ level}\cdot (1-\frac{d+1}{N})$ ，类似的 $\overline{E_{out}}=\mathbf{noise}\text{ level}\cdot (1+\frac{d+1}{N})$

从 $\overline{E_{in}}$ 和 $\overline{E_{out}}$ 我们可以推导出这样的图形：

• 
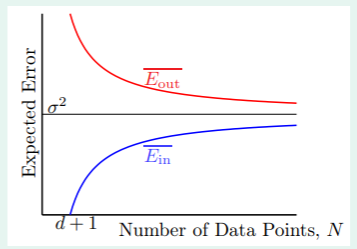
• 这说明随着样本数 N 的增大，$\overline{E_{in}}$ 在增大，$\overline{E_{out}}$ 在减小，并且双向奔赴，趋近于 ${\sigma }^2=\mathbf{noise}\text{ level}$ ，因此 $E_{in}$ 与 $E_{out}$ 的差距的期望为 $\frac{2(d+1)}{N}$ ；

终于，Linear Regression 能够成立得证！

练习：直觉理解 Hat Matrix

Linear Regression for Binary Classification

回顾一下线性分类和线性回归两种模型的特点：

• 

它们看起来既有区别，又有联系。其中一个重要的区别是，线性回归的计算效率很高，而线性分类是 NP-hard 的复杂度，那么能否使用线性回归来运用到线性分类中呢？思路如下：

• 将线性分类的输出也看做线性回归输出的实数集的一部分：$\{+1,-1\}\subset \mathbb{R}$
• 在二元分类数据集 $\mathcal{D}$ 上运行线性回归算法
• 返回 $g(\mathbf{x})=\text{sign}({\mathbf{w}}_{LIN}^T\mathbf{x})$

Heuristic

试着分析这种启发式（heuristic）学习的可行性：

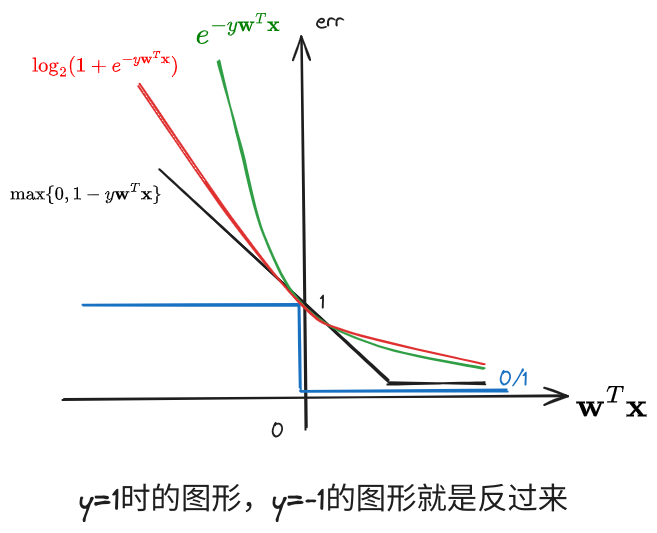
• 二元分类的错误评估是 ${\text{err}}_{0/1}=\left[\text{sign}({\mathbf{w}}^T\mathbf{x})\ne y\right]$ ，线性回归的错误评估是 ${\text{err}}_{s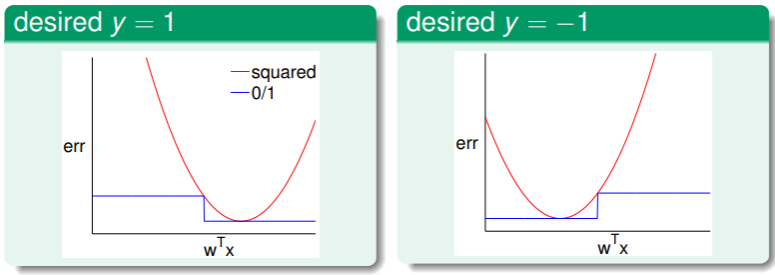qr}=({\mathbf{w}}^T\mathbf{x}-y{)}^2$ ，他们的函数图像是： 可以看出，${\text{err}}_{0/1}\le {\text{err}}_{sqr}$ ，那么我们联系之前 VC Dimension 的内容，其中对分类问题的错误概率作出估计是：

$$\text{classification }{E}_{out}(\mathbf{w})\stackrel{VC}{\le }\text{classification }{E}_{in}(\mathbf{w})+\sqrt{\frac{8}{N}\ln (\frac{4(2N{)}^{d_{VC}}}{\delta })}$$

，如果进一步放宽 upper bound，以 ${\text{err}}_{sqr}$ 代之，则得到

$$\text{classification }{E}_{out}(\mathbf{w})\stackrel{VC}{\le }\text{regression }{E}_{in}(\mathbf{w})+\sqrt{\frac{8}{N}\ln (\frac{4(2N{)}^{d_{VC}}}{\delta })}$$

，此时，我们能够通过线性回归算法以较高的效率获得一个较宽的上界，因此若将 ${\mathbf{w}}_{LIN}$ 作为基准，即二元分类中的 ${\mathbf{w}}_0$ ，然后从此迭代，就可以有效地降低 PLA/Pokcet 算法的执行时间。

练习：二元分类问题的错误上界

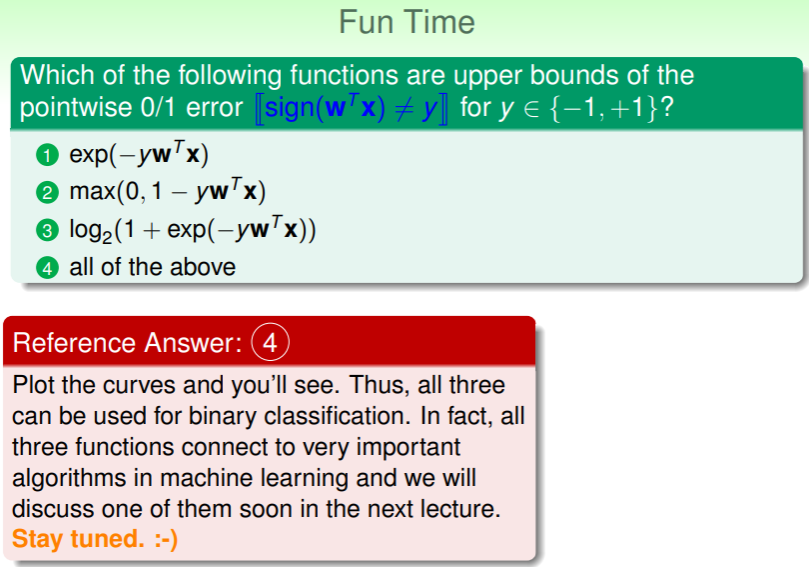
• 下面是 $y=1$ 时的图形：