What is Clos Network？

In the field of telecommunications, a Clos network is a kind of multistage circuit-switching network which represents a theoretical idealization of practical, multistage switching systems. It was invented by Edson Erwin in 1938 and first formalized by the American engineer in 1952.

Clos 网络是一种多级电路交换网络。

By adding stages, a Clos network reduces the number of crosspoints required to compose a large crossbar switch. A Clos network topology (diagrammed below) is parameterized by three integers n, m, and r :

• n represents the number of sources which feed into each of r ingress stage crossbar switches;
• each ingress stage crossbar switch has m outlets; and there are m middle stage crossbar switches.

Clos 网络可减少组成大型 crossbar 交换机系统所需的交叉点数量。

Circuit switching arranges a dedicated communications path for a connection between endpoints for the duration of the connection. This sacrifices total bandwidth available if the dedicated connections are poorly utilized, but makes the connection and bandwidth more predictable, and only introduces control overhead when the connections are initiated, rather than with every packet handled, as in modern packet-switched networks.

电路交换的作用是在连接期间为端点之间的连接安排专用的通信路径。

如果专用连接的利用率不高，就会牺牲可用的总带宽，但会使连接和带宽更可预测，而且只在启动连接时引入控制开销，而不是像现代分组交换网络那样，在处理每个数据包时都引入控制开销。

When the Clos network was first devised, the number of crosspoints was a good approximation of the total cost of the switching system. While this was important for electromechanical crossbars, it became less relevant with the advent of VLSI (very-large-scale integration), wherein the interconnects could be implemented either directly in silicon, or within a relatively small cluster of boards. Upon the advent of complex data centers, with huge interconnect structures, each based on optical fiber links, Clos networks regained importance. A subtype of Clos network, the Beneš network, has also found recent application in machine learning.

在最初设计 Clos 网络时，交叉点的数量是交换系统总成本的一个很好的近似值。

虽然这对机电 electromechanical crossbars 来说很重要，但随着超大规模集成电路（VLSI）的出现，这一点就变得不那么重要了，因为在 VLSI 中，互连可以直接在硅片中实现，或者在相对较小的电路板群中实现。

复杂的数据中心拥有庞大的互联结构，每个结构都以光纤链路为基础，在这种情况下，Clos 网络重新得到重视。

Topology

Clos networks have three stages: the ingress stage, the middle stage, and the egress stage. Each stage is made up of a number of crossbar switches, often just called crossbars. The network implements an r-way perfect shuffle between stages. Each call entering an ingress crossbar switch can be routed through any of the available middle stage crossbar switches, to the relevant egress crossbar switch. A middle stage crossbar is available for a particular new call if both the link connecting the ingress switch to the middle stage switch, and the link connecting the middle stage switch to the egress switch, are free.

Clos 网络有三个阶段：入口阶段、中间阶段和出口阶段。 每个阶段都由若干个 crossbar 交换机组成，这些交换机也可简称为 crossbars 。

网络在各级之间实现了 r 路完美混洗。进入 ingress crossbar 交换机的每个呼叫都可以通过任何可用的 middle crossbar 交换机路由到相关的 egress crossbar 交换机。 如果连接入口交换机和中间交换机的链路以及连接中间阶段交换机和出口交换机的链路都空闲，则中间阶段的 crossbar 可用于特定的新呼叫。

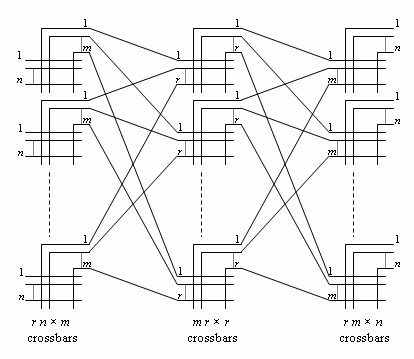
Clos networks are defined by three integers n, m, and r ：

• n represents the number of sources which feed into each of r ingress stage crossbar switches.
• Each ingress stage crossbar switch has m outlets, and there are m middle stage crossbar switches. There is exactly one connection between each ingress stage switch and each middle stage switch.
• There are r egress stage switches, each with m inputs and n outputs. Each middle stage switch is connected exactly once to each egress stage switch.

Thus, the ingress stage has r switches, each of which has n inputs and m outputs. The middle stage has m switches, each of which has r inputs and r outputs. The egress stage has r switches, each of which has m inputs and n outputs.

• n 代表进入 r 个入口级 crossbar 交换机的信号源数量。
• 每个入口级 crossbar 交换机有 m 个出口，中间级 crossbar 交换机有 m 个。 每个入口级交换机和每个中间级交换机之间正好有一个连接。
• 有 r 个出口级交换机，每个交换机有 m 个输入端和 n 个输出端。每个中间级交换机与每个出口级交换机精确连接一次。

因此，入口有 r 个交换机，每个交换机有 n 个输入和 m 个输出。 中间有 m 个交换机，每个交换机有 r 个输入和 r 个输出。 出口有 r 个交换机，每个交换机有 m 个输入和 n 个输出。

Blocking characteristics

The relative values of m and n define the blocking characteristics of the Clos network.

m 和 n 的相对值决定了 Clos 网络的阻塞特性。

Strict-sense nonblocking Clos networks ($m\ge 2n-1$): the original 1953 Clos result

If $m\ge 2n-1$, the Clos network is strict-sense nonblocking, meaning that an unused input on an ingress switch can always be connected to an unused output on an egress switch, without having to re-arrange existing calls. This is the result which formed the basis of Clos’s classic 1953 paper.

如果 $m\ge 2n-1$，Clos 网络就是严格意义上的无阻塞网络，这意味着入口交换机上未使用的输入始终可以连接到出口交换机上未使用的输出，而无需重新安排现有呼叫（连接）。这一结果正是 Clos 1953 年经典论文的基础。

Assume that there is a free terminal on the input of an ingress switch, and this has to be connected to a free terminal on a particular egress switch. In the worst case, $n-1$ other calls are active on the ingress switch in question, and $n-1$ other calls are active on the egress switch in question. Assume, also in the worst case, that each of these calls passes through a different middle-stage switch. Hence in the worst case, $2n-2$ of the middle stage switches are unable to carry the new call. Therefore, to ensure strict-sense nonblocking operation, another middle stage switch is required, making a total of $2n-1$.

假设入口交换机的输入端有一个空闲终端，该终端必须连接到某个出口交换机上的空闲终端。在最坏情况下，入口交换机上有 n-1 个其他呼叫处于活动状态，出口交换机上也有 n-1 个其他呼叫处于活动状态。同样假设在最坏情况下，这些呼叫中的每个呼叫都会经过不同的中间交换机。 因此，在最坏情况下，有 2n-2 个中间级交换机无法承载新的呼叫。因此，为了确保严格意义上的无阻塞运行，还需要另一个中间级交换机，这样总共需要 2n-1 个中间级交换机。

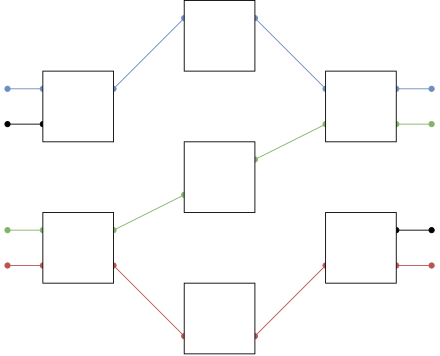
The below diagram shows the worst case when the already established calls (blue and red) are passing different middle-stage switches, so another middle-stage switch is necessary to establish a call between the green input and output.

下图显示了最坏的情况，即已建立的呼叫（蓝色和红色）通过不同的中间级交换机，因此需要另一个中间级交换机来建立绿色输入和输出之间的呼叫。

Rearrangeably nonblocking Clos networks ($m\ge n$)

If $m\ge n$, the Clos network is rearrangeably nonblocking, meaning that an unused input on an ingress switch can always be connected to an unused output on an egress switch, but for this to take place, existing calls may have to be rearranged by assigning them to different centre stage switches in the Clos network.

如果 $m\ge n$，则 Clos 网络是可重新排列的无阻塞网络，这意味着入口交换机上未使用的输入端始终可以连接到出口交换机上未使用的输出端，但要实现这一点，必须对现有呼叫进行重新排列，将其分配给 Clos 网络中的不同中心交换机。

To prove this, it is sufficient to consider m = n, with the Clos network fully utilised; that is, $r\times n$ calls in progress. The proof shows how any permutation of these $r\times n$ input terminals onto $r\times n$ output terminals may be broken down into smaller permutations which may each be implemented by the individual crossbar switches in a Clos network with m = n.

要证明这一点，只需考虑 m = n，Clos 网络得到充分利用的情景，即有 r×n 个呼叫正在进行。证明说明了 r×n 个输入终端到 r×n 个输出终端的任何排列都可以分解成更小的排列，每个排列都可以由 m = n 的 Clos 网络中的各个 crossbar 交换机来实现。

The proof uses Hall’s marriage theorem which is given this name because it is often explained as follows. Suppose there are r boys and r girls. The theorem states that if every subset of k boys (for each k such that 0 ≤ k ≤ r) between them know k or more girls, then each boy can be paired off with a girl that he knows. It is obvious that this is a necessary condition for pairing to take place; what is surprising is that it is sufficient.

证明利用了霍尔配婚定理——假设有 r 个男孩和 r 个女孩，该定理指出，如果他们之间的 k 个男孩的子集（对于每个 k，0 ≤ k ≤ r）都认识 k 个或更多的女孩，那么这些男孩都可以和他认识的女孩配对。很明显，这是配对发生的必要条件；令人惊讶的是，这也是充分条件。

In the context of a Clos network, each boy represents an ingress switch, and each girl represents an egress switch. A boy is said to know a girl if the corresponding ingress and egress switches carry the same call. Each set of k boys must know at least k girls because k ingress switches are carrying $k\times n$ calls and these cannot be carried by less than k egress switches. Hence each ingress switch can be paired off with an egress switch that carries the same call, via a one-to-one mapping. These r calls can be carried by one middle-stage switch. If this middle-stage switch is now removed from the Clos network, m is reduced by 1, and we are left with a smaller Clos network. The process then repeats itself until m = 1, and every call is assigned to a middle-stage switch.

在 Clos 网络中，每个男孩代表一个入口交换机，每个女孩代表一个出口交换机。 如果相应的入口交换机和出口交换机承载相同的呼叫，则称一个男孩认识一个女孩。 每组 k 个男孩必须至少认识 k 个女孩，因为 k 个入口交换机承载 k×n 个呼叫，而这些呼叫不可能由少于 k 个出口交换机承载。 因此，每个入口交换机都可以通过一对一映射与承载相同呼叫的出口交换机配对。这 r 个呼叫可由一个中间交换机承载。

如果现在将该中间交换机从 Clos 网络中移除，则 m 将减少 1，我们将得到一个更小的 Clos 网络。 然后重复上述过程，直到 m = 1，每个呼叫都分配给一个中间交换机。

Blocking probabilities: the Lee and Jacobaeus approximations

Real telephone switching systems are rarely strict-sense nonblocking for reasons of cost, and they have a small probability of blocking, which may be evaluated by the Lee or Jacobaeus approximations, assuming no rearrangements of existing calls. Here, the potential number of other active calls on each ingress or egress switch is $u=n-1$.

由于成本原因，真实的电话交换系统很少是严格意义上的无阻塞系统（$m\ge 2n-1$），它们有很小的阻塞概率，可以用李或雅各布近似法来评估。 这里，假设现有呼叫没有重新排列，每个入口或出口交换机上其他活跃的呼叫的潜在数量为 $u=n-1$。

In the Lee approximation, it is assumed that each internal link between stages is already occupied by a call with a certain probability $p$ , and that this is completely independent between different links. This overestimates the blocking probability, particularly for small $r$ . The probability that a given internal link is busy is $p=\frac{uq}{m}$, where $q$ is the probability that an ingress or egress link is busy. Conversely, the probability that a link is free is $1-p$. The probability that the path connecting an ingress switch to an egress switch via a particular middle stage switch is free is the probability that both links are free, $(1-p{)}^2$ . Hence the probability of it being unavailable is $1-(1-p{)}^2=2p-p^2$ . The probability of blocking, or the probability that no such path is free, is then $[1-(1-p{)}^2{]}^m$.

在 Lee 近似法中，假定每个阶段之间的内部链路都已被呼叫占用，占用概率为 $p$，且不同链路之间完全独立。这就高估了阻塞概率，尤其是在 $r$ 较小的情况下。给定内部链路繁忙的概率为 $p=\frac{uq}{m}$，其中 $q$ 是入口或出口链路繁忙的概率。反之，链路空闲的概率为 $1-p$。通过特定中级交换机连接入口交换机和出口交换机的路径空闲的概率是两条链路都空闲的概率 $(1-p{)}^2$，因此不可用的概率是 $1-(1-p{)}^2=2p-p^2$。 因此，阻塞概率或没有空闲路径的概率为 $[1-(1-p{)}^2{]}^m$。

The Jacobaeus approximation is more accurate, and to see how it is derived, assume that some particular mapping of calls entering the Clos network (input calls) already exists onto middle stage switches. This reflects the fact that only the relative configurations of ingress switch and egress switches is of relevance. There are $i$ input calls entering via the same ingress switch as the free input terminal to be connected, and there are $j$ calls leaving the Clos network (output calls) via the same egress switch as the free output terminal to be connected. Hence $0\le i\le u$, and $0\le j\le u$.

雅各布斯近似法更为精确，要了解它是如何得出的，可假设进入 Clos 网络的呼叫（输入呼叫）与中间交换机之间已经存在某种特定的映射关系。这反映了一个事实，即只有入口交换机和出口交换机的相对配置才是相关的。 有 $i$ 个输入呼叫通过与待连接的空闲输入终端相同的入口交换机进入，有 $j$ 个呼叫通过与待连接的空闲输出终端相同的出口交换机离开 Clos 网络（输出呼叫）。 因此，$0\le i\le u，0\le j\le u$。

Let $A$ be the number of ways of assigning the $j$ output calls to the $m$ middle stage switches. Let $B$ be the number of these assignments which result in blocking. This is the number of cases in which the remaining $m-j$ middle stage switches coincide with $m-j$ of the $i$ input calls, which is the number of subsets containing $m-j$ of these calls. Then the probability of blocking is:

设 $A$ 为将 $j$ 个输出调用分配给 $m$ 个中间级交换机的方法数。 设 $B$ 为这些分配方式中导致阻塞的方式数。 这就是剩余的 $m-j$ 个中间阶段交换机与 $i$ 个输入呼叫中的 $m-j$ 个呼叫重合的情况数，也就是包含这些呼叫中的 $m-j$ 个呼叫的子集数。 那么阻塞概率为

$${\beta }_{i,j}=\frac{B}{A}=\frac{\left(\genfrac{}{}{0ex}{}{i}{m-j}\right)}{\left(\genfrac{}{}{0ex}{}{m}{j}\right)}=\frac{i!j!}{(i+j-m)!}$$

If $f_i$ is the probability that $i$ other calls are already active on the ingress switch, and $g_j$ is the probability that $j$ other calls are already active on the egress switch, the overall blocking probability is:

如果 $f_i$ 是入口交换机上已有 $i$ 个其他呼叫处于活动状态的概率，$g_j$ 是出口交换机上已有 $j$ 个其他呼叫处于活动状态的概率，则总体阻塞概率为：

$$P_B=\sum _{i=0}^u\sum _{j=0}^u{f}_i{g}_i{\beta }_{i,j}$$

This may be evaluated with $f_i$ and $g_j$ each being denoted by a binomial distribution. After considerable algebraic manipulation, this may be written as:

这可以用 $f_i$ 和 $g_j$ 各自的二项分布来表示。经过大量的代数运算，可以写成

$$P_B=\frac{(u!{)}^2(2-p{)}^{2u-m}{p}^m}{m!(2u-m)!}$$

Clos networks with more than three stages

Clos networks may also be generalised to any odd number of stages. By replacing each centre stage crossbar switch with a 3-stage Clos network, Clos networks of five stages may be constructed. By applying the same process repeatedly, 7, 9, 11,… stages are possible.

Clos 网络也可推广到任何奇数级。 用 3 级 Clos 网络取代每个中间 crossbar 交换机，就可以构建 5 级 Clos 网络。通过重复应用相同的过程，可以实现 7 级、9 级、11 级…。

Beneš network (m = n = 2)

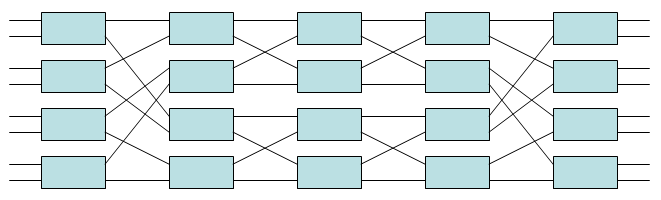
A rearrangeably nonblocking network of this type with m = n = 2 is generally called a Beneš network, even though it was discussed and analyzed by others before Václav E. Beneš. The number of inputs and outputs is $N=r\times n=2r$ . Such networks have $2{\log }_{2}N-1$ stages, each containing $\frac{N}{2}$ 2×2 crossbar switches, and use a total of $N{\log }_{2}N-\frac{N}{2}$ 2×2 crossbar switches. For example, an 8×8 Beneš network (i.e. with N = 8) is shown below; it has $2{\log }_{2}8-1=5$ stages, each containing $\frac{N}{2}=4$ 2×2 crossbar switches, and it uses a total of $N{\log }_{2}N-\frac{N}{2}=20$ 2×2 crossbar switches. The central three stages consist of two smaller 4×4 Beneš networks, while in the center stage, each 2×2 crossbar switch may itself be regarded as a 2×2 Beneš network. This example therefore highlights the recursive construction of this type of network.

尽管在瓦茨拉夫-E-贝尼斯（Václav E. Beneš）之前就有人讨论和分析过这种可重排的无阻塞网络，但它一般被称为贝尼斯网络（Beneš network）。输入和输出的数量为 $N=r\times n=2r$。 这样的网络有 $2{\log }_{2}N-1$ 级，每级包含 $\frac{N}{2}$ 个 2×2 crossbar 交换机，总共使用 $N{\log }_{2}N-\frac{N}{2}$ 个 2×2 crossbar 交换机。

例如，一个 8×8 的 Beneš 网络（即 N = 8）如下图所示；它有 $2{\log }_{2}8-1=5$ 级，每级包含 $\frac{N}{2}=4$ 个 2×2 crossbar 交换机，总共使用 $N{\log }_{2}N-\frac{N}{2}=20$ 个 2×2 crossbar 交换机。中间的三个阶段由两个较小的 4×4 贝涅斯网络组成，而在中间阶段，每个 2×2 crossbar 交换机本身可视为一个 2×2 贝涅斯网络。 因此，这个例子突出了这种网络的递归结构。

See also

• Banyan switch, an alternative way to connect networks
• Fat tree, an alternative way to connect networks
• Omega network, an alternative way to connect networks