69-Finger-Search

Introduction

In computer science, a finger search on a data structure is an extension of any search operation that structure supports, where a reference (finger) to an element in the data structure is given along with the query. While the search time for an element is most frequently expressed as a function of the number of elements in a data structure, finger search times are a function of the distance between the element and the finger.

Fig. Example of finger search on treaps.

In a set of n elements, the distance d(x,y) (or simply d when unambiguous) between two elements x and y is their difference in rank. If x and y are the ith and jth largest elements in the structure, then the difference in rank is |i - j|. If a normal search in some structure would normally take $O(f(n))$ time, then a finger search for x with finger y should ideally take $O(f(d))$ time. Remark that since d ≤ n, it follows that in the worst case, finger search is only as bad as normal search.

finger search 的时间复杂度与查找的两目标的连线距离 d 有关，在最坏情况下可能达到 $O(f(n))$ 量级。

However, in practice these degenerate finger searches do more work than normal searches. For instance, if f(n) is log(n), and finger search does twice as many comparisons as normal search in the worst case, it follows that finger search is slower when $d>\sqrt{n}$.

finger search 在退化情况的比较次数是普通搜索在最坏情况下的两倍。

Therefore, finger search should only be used when one can reasonably expect the target to actually be close to the finger.

Implementations

Some popular data structures support finger search with no additional changes to the actual structure. In structures where searching for an element x is accomplished by narrowing down an interval over which x can be found, finger search from y is typically accomplished by reversing the search process from y until the search interval is large enough to contain x, at which point search proceeds as normal.

数据结构中为了搜索 x ，是通过缩减能够找到 x 的区间来实现的，从 y 出发搜索 x 的 finger search 也是如此，不过却是逆转方向，从 y 逐渐增大区间直到涵盖 x。

Sorted linked lists

In a linked list, one normally searches linearly for an element by walking from one end to the other. If the linked list is sorted, and we have a reference to some node containing y, then we may find x in $O(d)$ time by starting our search from y.

Sorted arrays

In a sorted array A, one normally searches for an element x in A with a binary search. Finger search is accomplished by performing a one-sided search from A[j] = y. While binary search halves the search space after each comparison, one-sided search doubles the search space after each comparison. Specifically, on the kth iteration of one-sided search (assuming x > y), the interval under consideration is $A[j,j+2^{k-1}]$. Expansion halts as soon as $A[j+2^{k-1}]\ge x$, at which point this interval is binary searched for x.

有序向量中的常规搜索是二分搜索，而 finger search 则是从向量的一端 y 入手开始单边搜索。二分搜索每次比较后搜索空间减半，但单边搜索则在比较后搜索空间加倍。 具体来说，单边搜索的第 k 次迭代中（不妨设搜索起点 y < 搜索目标 x ），所考虑的区间为 $A[j,j+2^{k-1}]$，当 $A[j+2^{k-1}]\ge x$ 时，扩展停止，此时再对这个区间进行二分搜索。

If one-sided search takes k iterations to find an interval that contains x, then it follows that $d>2^{k-2}$. Binary searching this range will also take another k iterations. Therefore, finger search for x from y takes $O(k)=O(\log d)$ time.

如果单边搜索进行了 k 轮迭代才找到容纳 x 的区间，这表明 y 和 x 之间的举例大于 $2^{k-2}$。在这个区间内二分搜索将会再一次需要 k 轮迭代。 因此，finger search 需要 $O(k)=O(\log d)$ 的时间。

Skip lists

In a skip list, one can finger search for x from a node containing the element y by simply continuing the search from this point. Note that if x < y, then search proceeds backwards, and if x > y, then search proceeds forwards. The backwards case is symmetric to normal search in a skip list, but the forward case is actually more complex.

跳转表中从 y 搜索 x，可能向前也可能向后，向前搜索与正常的搜索没什么两样，但向后搜索较为复杂。

Normally, search in a skiplist is expected to be fast because the sentinel(哨兵) at the start of the list is as tall as the tallest node. However, our finger could be a node of height 1. Because of this, we may occasionally climb while trying to search; something which never occurs normally. However, even with this complication, we can achieve O (log d) expected search time.¹

正常搜索时起始点是哨兵（起始处高度为正无穷），但 finger search 时起始处可能高度只有 1，因此这可能涉及到向上攀升跳转表。但总而言之，也能够实现 $O(\log d)$ 的复杂度。

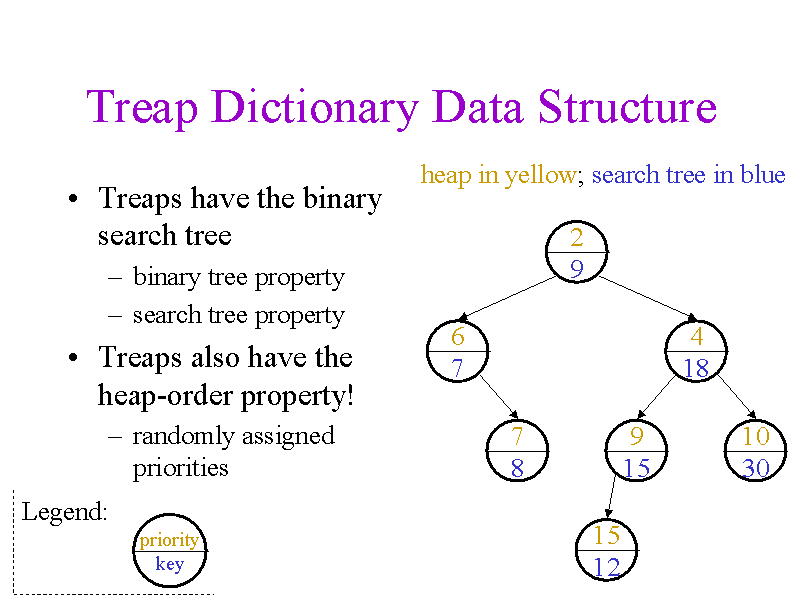
Treaps

Treap = Tree + Heap

A treap is a randomized binary search tree (BST). Searching in a treap is the same as searching for an element in any other BST. Treaps however have the property that the expected path length between two elements of distance d is O (log d). Thus, to finger search from the node containing y for x, one can climb the tree from y until an ancestor of x is found, at which point normal BST search proceeds as usual.

Treap 的特点就是任意两个距离为 d 的元素之间，预期路径长度为 $O(\log d)$

While determining if a node is the ancestor of another is non-trivial, one may augment the tree to support queries of this form to give expected O (log d) finger search time.

尽管决定一个节点是否是另一个节点的祖先并不容易，但可以通过增强树来支持这种形式的查询，得到 $O(\log d)$ 的查询时间。

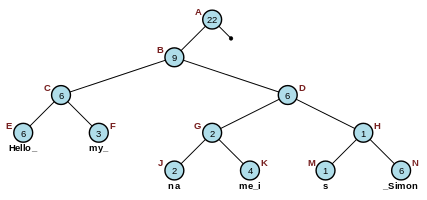
Ropes and trees

A simple rope built on the string of “Hello_my_name_is_Simon”.

Implementations of the rope (data structure) typically implement a cord position iterator to traverse the string. The iterator can be seen as a finger that points at some specific character of the string. Like most balanced trees, ropes require O (log (n)) time to retrieve data in one leaf of the tree when given only the root of the tree. Reading every leaf of the tree would seem to require O (nlog (n)) time.

rope 结构通过绳索位置迭代器来遍历字符串，迭代器可以看作是指向字符串中某个特定字符的 finger。类似于大多数平衡树，rope 需要 $O(\log n)$ 的时间从根搜索到叶子，因此似乎遍历所有叶节点需要 $O(n\log n)$ 的时间。

However, by storing a little extra information, the iterator can be used to read “the next” leaf in only O (1) time, and every leaf of a tree in only O (n) time. Implementations of ropes typically cache “extra information” about the entire the path from the root to the current node position in the iterator.

不过，通过存储一些额外信息，迭代器只需 O (1) 次就能读取 “下一片 “叶子，而读取树的每一片叶子只需 O (n) 次。绳索的实现通常会在迭代器中缓存从根节点到当前节点位置的整个路径的 “额外信息”。

Other implementations of tree data structures sometimes store “extra information” in the tree itself, storing a pointer in each node to its parent or its successor (in addition to the normal pointers in each node to its children), and storing only the current node position in the iterator.^{2 3}

Generalizations

If one can perform finger search in an iterative manner in O(f(d)) time, where each iteration takes O(1) time, then by providing c different fingers, one can perform finger search in $O(c\times min\{d(x,y_1),...,d(x,y_c)\})$ time. This is accomplished by starting finger search for all c fingers, and iterating them forward one step each until the first one terminates.

Given any sequence $A=[a_1,...,a_m]$ of m accesses, a structure is said to have the static finger property for a fixed finger f, if the time to perform A is $O\left(\sum _{i=1}^m\log d(f,a_i)\right)$.

给定 m 个访问的任一序列 A，如果执行访问完 A 的时间为 $O\left(\sum _{i=1}^m\log d(f,a_i)\right)$，那么对于这个固定的 f，这个数据结构具有静态 finger 属性。

Splay trees have this property for any choice of f with no additional processing on sufficiently large sequences of accesses.

对于任何 f 的选择，伸展树都具有这种特性，在足够大的访问序列中无需额外处理。

Applications

Finger search can be used to re-use work already done in previous searches. For instance, one way to iterate over the elements in a data structure is to simply finger search for them in order, where the finger for one query is the location of the result of the last. One may optimize their data structure by doing this internally if it is known that searches are frequently near the last search.

finger search 可重复使用以前搜索中已完成的工作。例如，对数据结构中的元素进行迭代的一种方法就是简单地按顺序对它们进行 finger search，其中一次查询的 finger 位置就是上一次查询结果的位置。如果知道搜索结果经常靠近上一次搜索结果，那么就可以通过内部搜索来优化数据结构。

A finger search tree is a type of data structure that allows fingers to be specified such that all or some of their supported operations are faster when they access or modify a location near a finger. In contrast to the finger searches described in this article, these fingers are not provided at query time, but are separately specified so that all future operations use these fingers. One benefit of this is that the user needs not manipulate or store internal references to the structure, they may simply specify an element in the structure.

finger 搜索树是一种允许指定 finger 的数据结构，当访问或修改 finger 附近的位置时，其支持的所有或部分操作都会更快。与本文所述的手指搜索不同，这些 finger 不是在查询时提供的，而是单独指定的，以便今后的所有操作都使用这些 finger 。这样做的一个好处是，用户无需操作或存储结构的内部引用，只需指定结构中的一个元素即可。

Footnotes

1. cs.au.dk/~gerth/papers/finger05.pdf ↩

2. General design concerns for a tree iterator ↩

3. Steven J. Zeil. “Traversing Trees with Iterators” Archived 2016-02-16 at the Wayback Machine. ↩