Introduction
B*-tree of order m is a search tree that is either empty or that satisfies three properties:
- The root node has minimum two and maximum 2 floor ((2m-2)/3) +1 children
- Other internal nodes have the minimum floor ((2m-1)/3) and maximum m children
- All external nodes are on the same level.
The advantage of using B* trees over B-trees is a unique feature called the ‘two-to-three’ split. By this, the minimum number of keys in each node is not half the maximum number, but two-thirds of it, making data far more compact. However, the disadvantage of this is a complex deletion operation.
The difficulties in practically implementing a B-star algorithm contribute to why it’s not as regularly used as its B and B+ counterparts.
Below is a basic implementation of the B-star insertion function – just to demonstrate its contrast from B (full implementation would be far more lengthy and complex).
The unique parts of the algorithm for B Tree insertion are as follows:*
Two-Three Split
1. If inserting into a full leaf node (which is not the root) and which has a full right sibling (and whose parent has at least one free key):
- Take an array (‘marray’) consisting of ‘m-1’ keys of the full leaf-node, the parent key of this node, the new key to be inserted, and the ‘m-1’ keys of its right sibling (Totally m-1 + 1 + 1 + m-1 = 2m keys)
- Sort these keys
- Create three new nodes:
- p – whose keys are the first (2m – 2)/3 elements of ‘marray’
The element at index (2m – 2)/3 is stored as ‘parent1’ - q – whose keys are the next (2m – 1)/3 elements of ‘marray’ after parent1
The element at index (4m)/3 is stored as ‘parent2’ - r – whose keys are the last (2m)/3 elements of ‘marray’ after parent2
- p – whose keys are the first (2m – 2)/3 elements of ‘marray’
- The key in the leaf’s parent which points to this leaf should have its value replaced as ‘parent1’
- If the parent key in iv) has any adjacent keys, they should be shifted to the right. In the space that remains, place ‘parent2’.
- p, q and r must be made child keys of parent1 and parent2 (if ‘parent1’ and ‘parent2’ are the first two keys in the parent node), else p, q, r must be made the child keys of the key before parent 1, parent 1, and parent 2 respectively.
Before Insertion :
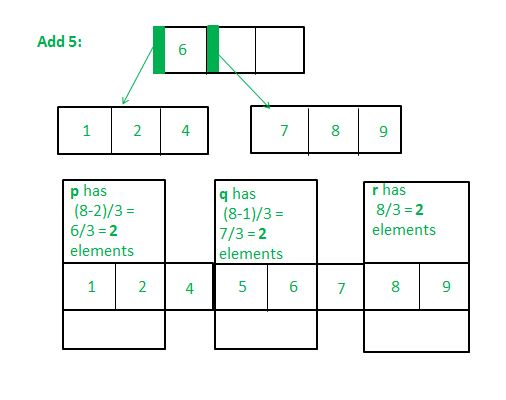
After insertion:
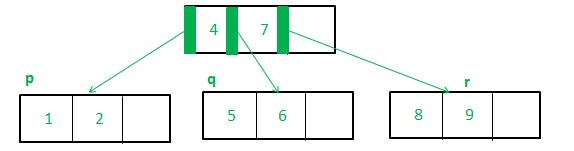
2. If inserting into a full leaf node (which is not the root) with empty/non-full right sibling.
- Simply shift the last element of the current node to the position of the parent, shift all the keys in the right sibling to the right, and insert the previous parent. Now, use the gap in your own node to rearrange and fit in the new key.
3. The other cases are the same as for B-Trees.
Examples:
Input: Add 4 to 1 2 3 L 5 R 7 8 9
Output: 1 2 L 3 7 R 4 5 R 8 9
3 and 7 become the parent keys by the two-three splitInput : Add 5 to 2 3 4 L 6 R 8 9 11
Output : 2 3 L 4 8 R 5 6 R 9 11
3 and 6 become the parent keys by the two-three split
Implementation
Below is the implementation of the above approach:
// CPP program to implement B* tree
#include <bits/stdc++.h>
using namespace std;
// This can be changed to any value -
// it is the order of the B* Tree
#define N 4
struct node {
// key of N-1 nodes
int key[N - 1];
// Child array of 'N' length
struct node* child[N];
// To state whether a leaf or not; if node
// is a leaf, isleaf=1 else isleaf=0
int isleaf;
// Counts the number of filled keys in a node
int n;
// Keeps track of the parent node
struct node* parent;
};
// This function searches for the leaf
// into which to insert element 'k'
struct node* searchforleaf(struct node* root, int k,
struct node* parent, int chindex)
{
if (root) {
// If the passed root is a leaf node, then
// k can be inserted in this node itself
if (root->isleaf == 1)
return root;
// If the passed root is not a leaf node,
// implying there are one or more children
else {
int i;
/*If passed root's initial key is itself g
reater than the element to be inserted,
we need to insert to a new leaf left of the root*/
if (k < root->key[0])
root = searchforleaf(root->child[0], k, root, 0);
else
{
// Find the first key whose value is greater
// than the insertion value
// and insert into child of that key
for (i = 0; i < root->n; i++)
if (root->key[i] > k)
root = searchforleaf(root->child[i], k, root, i);
// If all the keys are less than the insertion
// key value, insert to the right of last key
if (root->key[i - 1] < k)
root = searchforleaf(root->child[i], k, root, i);
}
}
}
else {
// If the passed root is NULL (there is no such
// child node to search), then create a new leaf
// node in that location
struct node* newleaf = new struct node;
newleaf->isleaf = 1;
newleaf->n = 0;
parent->child[chindex] = newleaf;
newleaf->parent = parent;
return newleaf;
}
}
struct node* insert(struct node* root, int k)
{
if (root) {
struct node* p = searchforleaf(root, k, NULL, 0);
struct node* q = NULL;
int e = k;
// If the leaf node is empty, simply
// add the element and return
for (int e = k; p; p = p->parent) {
if (p->n == 0) {
p->key[0] = e;
p->n = 1;
return root;
}
// If number of filled keys is less than maximum
if (p->n < N - 1) {
int i;
for (i = 0; i < p->n; i++) {
if (p->key[i] > e) {
for (int j = p->n - 1; j >= i; j--)
p->key[j + 1] = p->key[j];
break;
}
}
p->key[i] = e;
p->n = p->n + 1;
return root;
}
// If number of filled keys is equal to maximum
// and it's not root and there is space in the parent
if (p->n == N - 1 && p->parent && p->parent->n < N) {
int m;
for (int i = 0; i < p->parent->n; i++)
if (p->parent->child[i] == p) {
m = i;
break;
}
// If right sibling is possible
if (m + 1 <= N - 1)
{
// q is the right sibling
q = p->parent->child[m + 1];
if (q) {
// If right sibling is full
if (q->n == N - 1) {
struct node* r = new struct node;
int* z = new int[((2 * N) / 3)];
int parent1, parent2;
int* marray = new int[2 * N];
int i;
for (i = 0; i < p->n; i++)
marray[i] = p->key[i];
int fege = i;
marray[i] = e;
marray[i + 1] = p->parent->key[m];
for (int j = i + 2; j < ((i + 2) + (q->n)); j++)
marray[j] = q->key[j - (i + 2)];
// marray=bubblesort(marray, 2*N)
// a more rigorous implementation will
// sort these elements
// Put first (2*N-2)/3 elements into keys of p
for (int i = 0; i < (2 * N - 2) / 3; i++)
p->key[i] = marray[i];
parent1 = marray[(2 * N - 2) / 3];
// Put next (2*N-1)/3 elements into keys of q
for (int j = ((2 * N - 2) / 3) + 1; j < (4 * N) / 3; j++)
q->key[j - ((2 * N - 2) / 3 + 1)] = marray[j];
parent2 = marray[(4 * N) / 3];
// Put last (2*N)/3 elements into keys of r
for (int f = ((4 * N) / 3 + 1); f < 2 * N; f++)
r->key[f - ((4 * N) / 3 + 1)] = marray[f];
// Because m=0 and m=1 are children of the same key,
// a special case is made for them
if (m == 0 || m == 1) {
p->parent->key[0] = parent1;
p->parent->key[1] = parent2;
p->parent->child[0] = p;
p->parent->child[1] = q;
p->parent->child[2] = r;
return root;
}
else {
p->parent->key[m - 1] = parent1;
p->parent->key[m] = parent2;
p->parent->child[m - 1] = p;
p->parent->child[m] = q;
p->parent->child[m + 1] = r;
return root;
}
}
}
else // If right sibling is not full
{
int put;
if (m == 0 || m == 1)
put = p->parent->key[0];
else
put = p->parent->key[m - 1];
for (int j = (q->n) - 1; j >= 1; j--)
q->key[j + 1] = q->key[j];
q->key[0] = put;
p->parent->key[m == 0 ? m : m - 1] = p->key[p->n - 1];
}
}
}
}
/*Cases of root splitting, etc. are omitted
as this implementation is just to demonstrate
the two-three split operation*/
}
else
{
// Create new node if root is NULL
struct node* root = new struct node;
root->key[0] = k;
root->isleaf = 1;
root->n = 1;
root->parent = NULL;
}
}
// Driver code
int main()
{
/* Consider the following tree that has been obtained
from some root split:
6
/ \
1 2 4 7 8 9
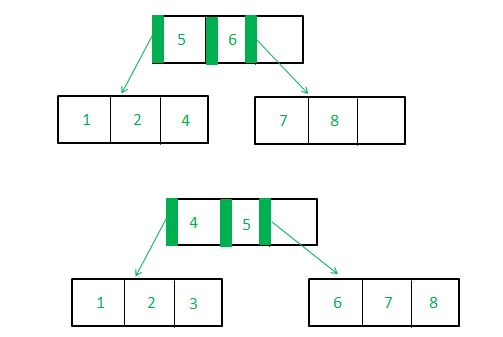
We wish to add 5. This makes the B*-tree:
4 7
/ \ \
1 2 5 6 8 9
Contrast this with the equivalent B-tree, in which
some nodes are less than half full
4 6
/ \ \
1 2 5 7 8 9
*/
// Start with an empty root
struct node* root = NULL;
// Insert 6
root = insert(root, 6);
// Insert 1, 2, 4 to the left of 6
root->child[0] = insert(root->child[0], 1);
root->child[0] = insert(root->child[0], 2);
root->child[0] = insert(root->child[0], 4);
root->child[0]->parent = root;
// Insert 7, 8, 9 to the right of 6
root->child[1] = insert(root->child[1], 7);
root->child[1] = insert(root->child[1], 8);
root->child[1] = insert(root->child[1], 9);
root->child[1]->parent = root;
cout << "Original tree: " << endl;
for (int i = 0; i < root->n; i++)
cout << root->key[i] << " ";
cout << endl;
for (int i = 0; i < 2; i++) {
cout << root->child[i]->key[0] << " ";
cout << root->child[i]->key[1] << " ";
cout << root->child[i]->key[2] << " ";
}
cout << endl;
cout << "After adding 5: " << endl;
// Inserting element '5':
root->child[0] = insert(root->child[0], 5);
// Printing nodes
for (int i = 0; i <= root->n; i++)
cout << root->key[i] << " ";
cout << endl;
for (int i = 0; i < N - 1; i++) {
cout << root->child[i]->key[0] << " ";
cout << root->child[i]->key[1] << " ";
}
return 0;
}
Output:
Original Tree:
6
1 2 4 7 8 9
After adding 5:
4 7
1 2 5 6 8 9