91-PQ-Exercise

10-2 哨兵处理越界

描述：基于向量实现完全二叉堆时，也可在向量中将各节点依次后移一个单元，并在腾出的首单元中置入对应元素类型的最大值作为哨兵（比如，对于整型可取 INT_MAX）。如此，虽然多使用了一个单元，但在上滤过程中只需比较父子节点的大小，而无需核对是否已经越界。

1. 如此转换后，父子节点在物理上的秩之间换算关系如何调整？ 具体地，若节点 v 的编号（秩）记作 i(v)，则根节点及其后代节点的编号分别为：

• i (root) = 1
• i (lchild (root)) = 2
• i (rchild (root)) = 3
• i (lchild (lchild (root)) = 4 …

一般地有：

1. 若节点 v 有左孩子，则 i (lchild (v)) = 2∙i (v)；
2. 若节点 v 有右孩子，则 i (rchild (v)) = 2∙i (v) + 1；
3. 若节点 v 有父节点，则 i (parent (v)) = $\lfloor \frac{i(v)}{2}\rfloor$ = $\lceil \frac{i(v)-1}{2}\rceil$;

2. 如此改进后，insert 和 delMax 操作时间复杂度有何变化？ 如此调整之后，上滤的过程无需核对是否已经越界，因此可以在一定程度上提高插入操作的效率，但渐进时间复杂度依然保持为 O(logn)。当然，以上调整对下滤的过程及效率没有影响。

3. 对于不易甚至无法定义最大值的元素类型，上述技巧不再适用。

10-3 降低上滤、下滤操作中 swap 的赋值次数

描述：percolateUp、percolateDown 算法中，若实际上升或下降 k = O(logn)层，则 k 次 swap()操作共需 3k 次赋值。 试改进以上实现，将此类赋值操作降至 k + 1 次。

在插入接口的上滤过程中，新元素可暂且不予插入，而只是将其上若干代祖先节点依次下移；待所有祖先均已就位之后，才将新元素置入腾出的空节点。删除接口的下滤过程，与此同理。

10-4 O (1)时间确定祖先的秩

考查基于向量实现的任一完全二叉堆。 我们注意到，其中祖先与后代节点的秩之间存在某种关联关系。具体地，只需令各节点的秩统一地递增一个单位，则从秩的二进制表示的角度来看，祖先必是后代的前缀。 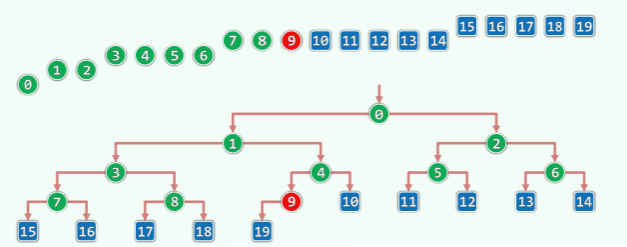以如图所示的完全二叉堆为例，考查其中节点18所对应的查找路径： 沿途各节点的秩依次为： 0, 1, 3, 8, 18 统一递增之后，依次为： 1, 2, 4, 9, 19 对应的二进制表示依次为： 1, 10, 100, 1001, 10011

可以看到，位数依次递增。而且更重要的是，相邻的每一对中，前者总是后者的前缀。 因此，对于任何秩为r的元素，其上溯第h代祖先（若存在）所对应的秩必然为： ((r + 1) >> h) - 1

10-4-b 将 percolateUp 算法的比较次数优化到 O (loglogn)

由上一题指出的特性，在引入新节点但尚未上滤调整之前，可以将该节点对应的查找路径视作一个静态查询表，并使用二分查找算法。

具体地，每次都可在 O(1)时间内确定高度居中的祖先的秩；将其当作轴点，只需再做 O(1) 次比较，即可将查找范围缩小一半。如此反复迭代，直至查找范围内仅剩单个节点。

既然完全二叉堆的高度 h = O(logn)，故整个查找过程的迭代（比较操作）次数将不超过： logh = O(loglogn)

请注意，因为任一节点通往其后代的路径并不唯一，故这一技巧并不适用于下滤操作。

1. 如此改进后，percolateUp 算法的总体渐进复杂度是否优化？ 以上方法固然可以有效地减少词条的比较操作，但词条交换操作却不能减少。事实上无论何，在最坏情况下，依然需要执行 O(h) = O(logn)次交换操作。

由此可见，percolateUp 算法总体的渐进复杂度将保持不变。

2. 通过实验确定，上述改进在完全二叉堆达到多大规模后才能体现出效果。 请读者独立完成编码和调试工作，并根据实测结果给出分析和结论。

需要指出的是，对于通常的应用问题规模 n 而言，logn 与 loglogn 均已十分接近于常数，二者之间的差异并不明显。 以 n = 2^32 = 4 * 10^9为例，有： ${\log }_{2}n=32$ , ${\log }_2({\log }_{2}n)=5$ 若再综合考虑到以上方法针对秩所额外引入的计算量，实际性能的差异将更不明显。

10-6 估算 percolateUp 的实际期望

描述：percolateUp()上滤算法，曾指出其执行时间为 O(logn)。然而，这只是对其最坏情况的估计；在通常的情况下，实际效率要远高于此。 试通过估算说明，在关键码均匀独立分布时，最坏情况极其罕见，且插入操作平均仅需常数时间。

在此仅做一个粗略的估算。 根据堆的定义及调整规则，若新节点 p 通过上滤升高了 k 层，则意味着在2^(k+1)个随机节点（p 的父亲、p，以及 p 的2^(k+1)- 2个后代）中，该节点恰好是第二大者。

于是，若将新节点累计上升的高度记作H，则H恰好为k的概率应为： Pr(H = k) = 1/2^(k+1) = (1/2)^k∙(1/2), 0 ⇐ k 这是一个典型的几何分布（geometric distribution），其数学期望为：E(H) = 1/(1/2) - 1 = 1

也就是说，每个节点经上滤后平均大致上升1层，其间平均需做1 + 1 = 2次比较操作。

10-7 Floyd 建堆法中同层内部节点下滤次序的影响

1. Floyd 建堆算法中，同层内部节点下滤的次序对建堆结果有无影响？若无影响，试说明原因；否则，试举一实例。 没有影响。 同层节点的下滤，仅涉及到其各自的后代，它们之间完全相互独立，故改变次序不致影响最终的结果。

2. 对建堆时间有无影响？ 也没有影响。 每个节点的下滤过程完全不变，所需时间不变，建堆所需的总体时间亦不变。

10-8 优先级队列与 Huffman 树

若将 Huffman 森林视作优先级队列，则其中每一棵树（每一个超字符）即是一个词条。为保 证词条之间可以相互比较，可如代码5.29（145页）所示重载对应的操作符。进一步地，因超字 符的优先级可度量为其对应权重的负值，故不妨将大小关系颠倒过来，令小权重超字符的优先级 更高，以便于操作接口的统一。 经上述准备，如下代码即可基于统一优先级队列接口给出通用的 Huffman 编码算法：

/************************************
 * Huffman树构造算法：对传入的Huffman森林forest逐步合并，直到成为一棵树
 ************************************
 * forest基于优先级队列实现，此算法适用于符合PQ接口的任何实现方式
 * 为Huffman_PQ_List、Huffman_PQ_ComplHeap和Huffman_PQ_LeftHeap共用
 * 编译前对应工程只需设置相应标志：DSA_PQ_List、DSA_PQ_ComplHeap或DSA_PQ_LeftHeap
 ************************************/
 
HuffTree* generateTree ( HuffForest* forest ) {
   while ( 1 < forest->size() ) {
      HuffTree* s1 = forest->delMax(); HuffTree* s2 = forest->delMax();
      HuffTree* s = new HuffTree();
      /*DSA*/printf ( "Merging " ); print ( s1->root()->data ); printf ( " with " ); print ( s2->root()->data ); printf ( " ...\n" );
      s->insert ( HuffChar ( '^', s1->root()->data.weight + s2->root()->data.weight ) );
      s->attach ( s1, s->root() ); s->attach ( s->root(), s2 );
      forest->insert ( s ); //将合并后的Huffman树插回Huffman森林
   }
   HuffTree* tree = forest->delMax(); //至此，森林中的最后一棵树
   return tree; //即全局Huffman编码树
}

相对于如代码5.36（147页）所示的版本，这里只不过将 minHChar()替换为 PQ::delMax() 标准接口。优先级队列的所有 ADT 操作均可在 O(logn)时间内完成，故 generateTree()算法也相应地可在 O(nlogn)时间内构造出 Huffman 编码树——较之原版本，改进显著。

1. 试证明，任何 CBA 式 Huffman 树构造算法，在最坏情况下都需要运行Ω(nlogn)时间。 只需建立一个从排序问题，到 Huffman 编码问题的线性归约（习题2-12）。

事实上，对于每一个待排序的输入序列，我们都将其视作一组字符的出现频率。不失一般性， 这里可以假设每个元素均非负——否则，可以在 O(n)时间内令它们增加同一足够大的正数。

以下，以这组频率作为输入，可以调用任何 CBA 式算法构造出 Huffman 编码树。而一旦得到这样一棵编码树，只需一趟层次遍历，即可在 O(n)的时间内得到所有（叶）节点的遍历序列。 根据 Huffman 树的定义，该序列必然是单调的。因此，整个过程也等效于同时完成了对原输入序列的排序。

10-9 利用频率已有序的性质在 O (n)完成构建 Huffman 树

描述：在附加某些特定条件后，问题难度往往会有实质下降。比如，若待编码字符集已按出现频率排序，则 Huffman 编码可以更快完成。在编码过程中，始终将森林 F 中的树分为两类：单节点（尚未参与合并）和多节点（已合并过）。每经过一次迭代，后者虽不见得增多，但必然有一个新成员。

1. 试证明，后一类树中，新成员的权重（频率）总是最大 根据 Huffman 编码算法的原理，每次迭代都是在当前森林中选取权重最小的两棵树做合并。 因此，被选出的树的权重必然单调非降，故在当前所有（经合成生成的）多节点树中，最新者的 权重必然最大。

2. 试在有序序列中以 O (n)时间完成 Huffman 编码 将如上定义的两类节点，按权重次序组织为两个队列。 初始状态如图x10.1(a)所示，所有字符都按照权重非降的次序，存入单节点树的队列（左）；而多节点树的队列（右），直接置空。 此后的过程与常规的Huffman编码算法类似，也是反复地取出权重最小的两棵树，将其合并后插回森林。直至最后只剩一棵树。

这里与常规算法的本质不同，共有两点。首先，每次只需考查两个队列各自最前端的两棵树。 也就是说，每次只需检查不超过四棵树，即可在 O(1)的时间内挑选出整个森林中权重最小的两棵树。另外，这两棵树合并之后，直接作为末元素插入多节点树的队列。

根据 1) 的分析结论， 这样依然可以保持该队列的单调性。 作为一个完整的实例，图 x10.1(b~f)针对权重集{ 2, 5, 13, 16, 19, 37 }，依次给出 了算法各步迭代之后，两个队列的具体组成。最终构造出的 Huffman 编码树，如图(g)所示。

10-11 斜堆 skew heap

描述：与 AVL 树需要借助 bf 记录类似，左式堆也需要设置 npl 记录。然而在实际应用中，这一点既不自然，也影响代码开发与转换效率。实际上，仿照由 AVL 树引出伸展树的思路，可以在保留左式堆优点的前提下消除 npl 记录，新结构称作斜堆（skew heap）。

具体定义与实现可参考：95-Skew-heap.

10-14 HeapSort 稳定性分析

不是稳定的。 在反复摘除堆顶并将末词条转移至堆顶，然后做下滤的过程中，雷同词条之间的相对次序不再保持，故它们在最终所得排序序列中必然是“随机”排列的。 作为一个实例，不妨仿照教材296页的图10.10，考查对堆： { 5, 4, 1a, 1b, 1c } 的排序。不难验证，最终所得的排序结果为： { 1c, 1a, 1b, 4, 5 }

实际上更糟糕的是，以上“随机性”是堆排序算法固有的不足，难以通过该算法自身的调整予以改进。当然，这一问题也并非不能解决——比如，读者不妨参考习题6-23 中介绍的合成数（composite number）法、习题6-16 的扰动法，消除歧义后再排序。

10-16 利用优先级队列改进 Prim 算法

描述：若能注意到教材 6.11.5 节 Prim 算法中定义的“优先级数”恰好对应于优先级队列中元素的优先级，即可利用本章介绍的优先级队列，改进教材 177 页代码 6.8 所示的 O(n^2)版本。 具体地，可首先花费 O(n)时间，将起点 s 与其余顶点之间的 n - 1 条边组织为一个优先级队列 H。此后的每一步迭代中，叧需 O(logn)时间即可从 H 中取出优先级数最小的边（最短桥），并将对应的顶点转入最小支撑树中。不过，随后为了高效地对 H 中与刚转出顶点相关联的每一条边做松弛优化，需要增加一个 decrease(e)接口，在边 e 优先级数减少后将 H 重新调整成一个堆。

注意，decrease 接口不过是调小优先级后重新做一次下滤。

1. 试证明如此改进后 Prim 算法效率为 O ((n+e) logn)，非常适用于稀疏图 按照该算法，取出每个顶点需要O(logn)时间，累计O(nlogn)时间。 所有顶点的所有邻接顶点的松弛，在最坏情况下累计需要O(elogn)时间。 两项合计，即得题中结论。

2. 这种策略是否适合 Dijkstra 算法？ 同样适用，只需改用Diskstra算法的优先级更新规则。 事实上，推而广之，这种改进策略适用于任何基于优先级搜索（PFS）策略的算法。

10.17 利用多叉堆改进 Prim 算法

描述：多叉堆中，每个节点至多拥有 d>=3 个孩子，且优先级不低于任何一个孩子。

1. 试证明多叉堆 decrease ()接口的效率可改进至 $O({\log }_{d}n)$ 仿照二叉堆的方式实现多叉堆: 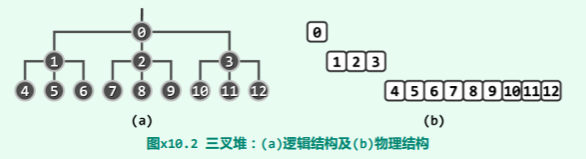具体地，将所有元素组织为一个向量，且对于任意秩为 k > 0的元素，其父亲对应的秩为： parent(k) = $\lfloor \frac{k-1}{d}\rfloor$

比如在图 x10.2所示的三叉堆中，8号元素的父亲对应的秩为：parent(8) = $\lfloor \frac{8-1}{3}\rfloor$ = 2

反过来，对于任意秩为 k < $\lceil \frac{n-1}{d}\rceil$ 的元素，其第 i 个孩子（若存在）对应的秩为： child(k, i) = k∙d + i, (i = 1, 2, …, d)

当然，当 d 不再是2的幂时，将不再能够借助移位运算来加速秩的换算。不过反过来，在计算效率并不主要依赖于秩换算效率的场合（比如数据规模大到跨越存储层次，涉及一定量的 I/O 操作时），这种推广完全行之有效。

按照以上实现方式，对于规模为 n 的 d 叉堆而言，高度应为： $\lceil {\log }_d(n\cdot (d-1)+1)\rceil -1=O({\log }_{d}n)$ 如此，在上滤过程中的每一步，只需将当前节点与其父节点做一次比较，因此整个上滤操作 总体的耗时量不过： $O({\log }_{d}n)$

与此同时，在下滤过程中的每一步，却需要遍历当前节点及其 d 个孩子，方可确定是否继续下降一层，以及向那个分支下降一层。相应地，总体耗时量为： $O(d)\cdot O({\log }_{d}n)=O(d\cdot {\log }_{d}n)$

2. ==试证明，若取 d=e/n+2，则基于 d-heap 实现的 Prim 算法时间复杂度可降低至== $O(e\cdot {\log }_{d}n)$ 根据以上分析，使用基于 d 叉堆的 Prim 算法，总体时间复杂度应为： $n\cdot d\cdot {\log }_{d}n+e\cdot {\log }_{d}n=(n\cdot d+e)\cdot {\log }_{d}n$

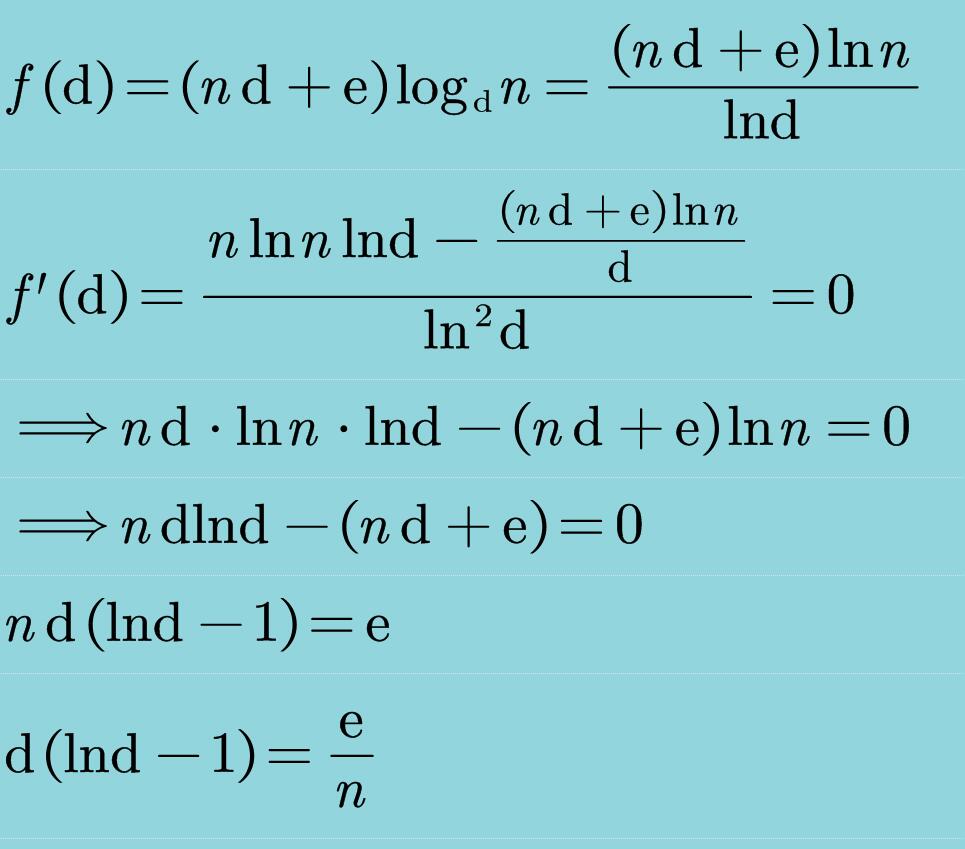特别地，当取： d = e/n + 2 时，总体的渐进性能将达到渐进最优的： $O(e\cdot {\log }_{d}n)=O(e\cdot {\log }_{\frac{e}{n+2}}n)$

3. 这种改进策略是否适用于 Dijkstra 算法？ 实际上，在基于优先级搜索（PFS）策略的图算法中，只要各节点优先级的更新方向总是单调非降（相应地，优先级数总是单调非升），则堆结构的上滤、下滤操作必然各自累计需要执行 O(e)次、O(n)次。在通常情况下，前者相对于后者都要更多（甚至非常多），故以上技巧及其性能分析的过程 和结论，亦将完全适用。在 Dijkstra 算法中，各节点优先级的更新方向也是单调非降的，故亦适用以上策略。

10-18 半无穷范围查询与优先级搜索树

描述：所谓半无穷范围查询（semi-infinite range query），是教材 8.4 节中所介绍一般性范围查询的特例。具体地，这里的查询区域是某一侧无界的广义矩形区域，比如 R = [-1, +1] x [0, +∞)，即是对称地包含正半 y 坐标轴、宽度为 2 的一个广义矩形区域。当然，对查询的语义功能要求依然不变——从某一相对固定的点集中，找出落在任意指定区域 R 内部的所有点。 范围树（习题[8-20]）稍作调整之后，固然也可支持半无穷范围查询，但若能针对这一特定问题所固有的性质，改用优先级搜索树（priority search tree, PST）之类数据结构，则不仅可以保持 O(r + logn)的最优时间效率，而且更重要的是，可以将空间复杂度从范围树的 O(nlogn)优化至 O(n)。 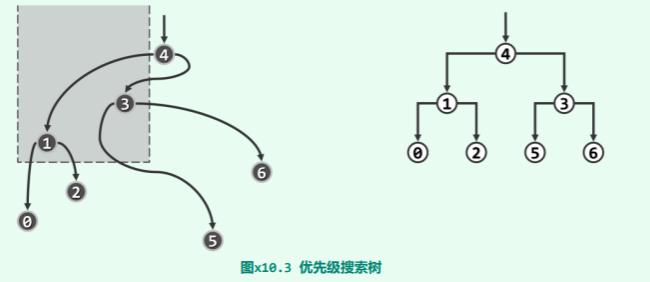如图 x10.3 所示，优先级搜索树除了首先在拓扑上应是一棵二叉树，还需同时遵守以下三条规则：

• 首先，各节点的 y 坐标均不小于其左、右孩子（如果存在）—— 因此，整体上可以视作为以 y 坐标为优先级的二叉堆
• 此外，相对于任一父节点，左子树中节点的 x 坐标均不得大于右子树中的节点
• 最后，互为兄弟的每一对左、右子树，在规模上相差不得超过一

1. 试设计算法，在 O (nlogn)时间内将平面上的 n 个点组织成一棵优先级搜索树； 首先，不妨按照 x 坐标对所有的点排序。然后，根据如上定义，可以递归地将这些点组织为一棵优先级搜索树。 具体地，为构造任一点集对应的子树，只需花费 O(n)时间从中找出最高（y 坐标最大）者， 并将其作为子树树根。以下，借助 x 坐标的排序序列，可以在 O(1)时间内将剩余的 n - 1个点均衡地划分为在空间上分列于左、右的两个子集——二者各自对应的子树，可以通过递归构造。 如此，构造全树所需的时间不超过： T(n) = 2∙T(n/2) + O(n) = O(nlogn)

2. 试设计算法，利用已创建的优先级搜索树，在 O (r+logn)时间内完成每次半无穷范围查询，其中 r 为实际命中并被报告的点数。

queryPST( PSTNode v, SemiInfRange R ) { //R = [x1, x2] x [y, +∞)
	if ( ! v || v.y < R.y ) return; //y-pruning
	if ( R.x1 < v.x && v.x < R.x2 ) output(v); //hit
	if ( R.x1 < v.xm ) queryPST( v.lc, R ); //recursion & x-pruning 
	if ( v.xm <= R.x2 ) queryPST( v.rc, R ); //recursion & x-pruning
}

首先，根据 y 坐标，判断当前子树根节点 v（及其后代）是否已经落在查询范围 R 之外。若是，则可立即在此处返回，不再深入递归——亦即纵向剪枝；否则，才需要继续深入查找。 以下，再检查根节点v的x坐标，若落在查询范围之内，则需报告该节点。 最后，若在节点 v 处的横向切分位置为 xm，则通过将其与 R 的左（x1）、右（x2）边界相比较，即可确认是否有必要继续沿对应的子树分支，继续递归搜索——亦即横向剪枝。

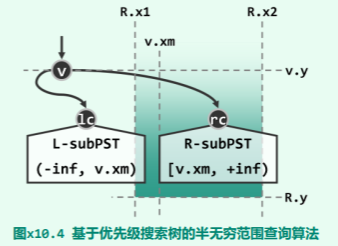
具体地如图 x10.4所示，唯有当 R.x1 位于 v.xm 左侧时，才有必要对左子树 v.lc 做递归搜索；唯有当 R.x2 不位于 v.xm 左侧时，才有必要对右子树 v.rc 做递归搜索。

对于任意的查询区域 R = [x1, x2] x [y, +∞) ，考查被算法 queryPST() 访问的任一节点，设与之对应的点为 v = (a, b)。于是，v 无非三种类型：

1. 被访问，且被报告出来——也就是说，v 落在 R 之内（x1 ⇐ a ⇐ x2 且 y ⇐ b）。此类节点恰有 r 个。
2. 虽被访问，却未予报告——因其 x 坐标落在 R 之外（a < x1 或 x2 < a）而横向剪枝，不再深入递归。此类节点在每一层上至多只有两个，总数不超过 O (2∙logn)。
3. 虽被访问，却未予报告——尽管其 x 坐标落在 R 之内（x1 ⇐ a ⇐ x2），但因其 y 坐标却未落在 R 之内（b < y）而纵向剪枝，也不深入递归。实际上，此类节点的父节点，必然属于 A 或 B 类，其总数不超过这两类节点总数的两倍。

综合以上分析可知，以上 queryPST()算法的渐进时间复杂度不超过 O(r + logn)。

10-19 为栈维护 getMax 接口

要求：保持 Stack::push 和 Stack::pop 等接口复杂度不变，在 O(1) 内定位并读取栈中最大元素。

如图 x10.5所示，对于任何一个栈 S，可以引入另一个与之孪生的“镜像”栈 P。 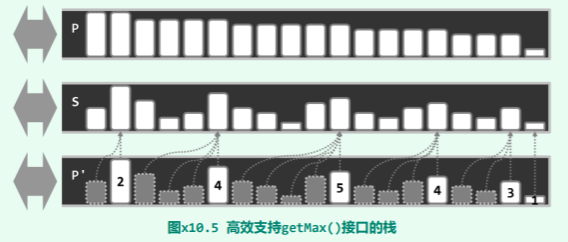具体地，P 中的元素与 S 中的元素始终保持一一对应，前者的取值，恰好就是后者所有前驱中的最大者。当然，P 中元素因此也必然按照单调非降的次序排列。如此，任何时刻栈 P 的顶元素，都是栈 S 中的最大元素。

为保持二者如上的对应关系，它们的 push()和 pop()操作必须同步进行：

1. 若执行：S.pop(); 则只需同步地执行： P.pop();
2. 而若执行： S.push( e ); 则需要同步地执行： P.push(max(e,P.top()));

以上方案还可以进一步地优化。 仍如图 x10.5所示，可将栈 P“压缩”为栈 P’。为此，需要注意到，P 中相等的元素必然彼此相邻，并因此可以分为若干组。若假想地令栈 P 中的每个元素通过指针指向栈 S 中对应的元素，而不是保留后者的副本，则可以将 P 中的同组元素合并起来，共享一个指针。当然，同时还需为合并后的元素增设一个计数器，记录原先同组元素的总数。

如此改进之后的“镜像”结构，如图中的栈 P’所示：每一组元素只需保留一份（白色）， 其余元素（灰色）则不必继续保存。这样，附加空间的使用量可以大为降低。

1. 相应地，在栈 S 每次执行出栈操作时，栈 P（P’）必须同步地执行： if （ ! ( -- P.top().counter ) ) P.pop();
2. 而在栈 S 每次执行入栈操作时，栈 P（P’）也必须同步地执行： P.top() < e ? P.push( e ), P.top().counter = 1 : P.top().counter ++;

可见，S 的 push()和 pop()接口，依然保持 O(1)的时间效率。

10-20 为队列维护 getMax 接口

要求：保持 Queue::dequeue 接口复杂度不变，Queue::enqueue 接口分摊为 O (1)，在 O (1) 内定位并读取队列中最大元素。

习题10-19 针对栈结构的技巧，可以推广至队列结构。比如，可以引入一个双端队列 P 并依然约定，其中每个元素也是始终指向队列 Q 中所有其前驱中的最大者。

为保持二者的对应关系，它们的 dequeue()和 enqueue()操作也必须同步进行：

1. 若执行：Q.dequeue(); 则只需同步地执行： P.removeFront();
2. 而若执行： Q.enqueue(e); 则只需同步地执行：

P.insertRear(e); 
for (x = P.rear(); x & (x.key <= e); x = x.pred) //for each rear element x no greater than e 
	x.key = e; //update its maximum record`

也就是说，除了首先也令 e 加入队列 P，而且还需要将 P 尾部所有不大于 e 的元素，统一更新为 e。 很遗憾，在最坏情况下这需要 Ω(n)时间。而且更糟糕的是，这种情况可能持续发生（读者不妨独立构造出这样的一个实例）。造成这一困难的原因在于，队列中任一元素的前驱集，不再如在栈中那样是固定的，而是可能增加、甚至新增的元素非常大。为此，可按照如图 x10.6 所示的思路进一步改进。 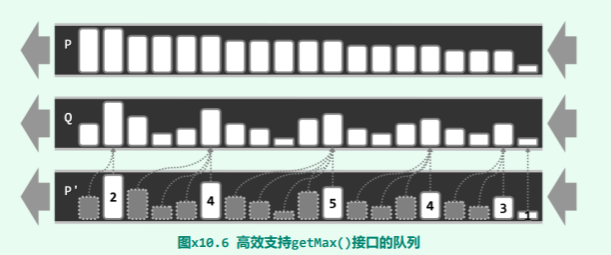具体地，可首先仿照 习题10-19 的改进技巧，通过合并相邻的同组元素，将队列 P 压缩为 队列 P’。然后，

• 在队列 Q 每次执行出队操作时，队列 P（P’）必须同步地执行： if (!(-- P.front().counter)) P.removeFront();
• 而在队列 Q 每次执行入队操作时，栈 P（P’）也必须同步地执行：

a = 1; //counter accumulator
while (!P.empty() && (P.rear().key <= e) //while the rear element is no greater than e 
	a += P.removeRear().counter; //accumulate its counter before removing it 
P.insertRear(e); 
P.rear().counter = a; 

这里的 while 循环，在最坏情况下仍然需要迭代 O(n)步，但因为参与迭代的元素必然随即被删除，故就分摊意义而言仅为 O(1)步，时间性能大为改善。

另外，这里的队列 P’并不需要具备双端队列的所有功能。实际上，它仅使用了 Deque 结构的 removeFront()、insertRear()和 removeRear()接口，而无需使用 insertFront()接口 —— 因此形象地说，它只不过是一个“1.5”端队列。

10-21 合并 AVL 树

说明：任给高度为 g 和 h 的两棵 AVL 树 S 和 T，其中 S 的节点均不大于 T 的节点。试设计算法，在 O (max (g, h))时间内合并为一棵 AVL 树。 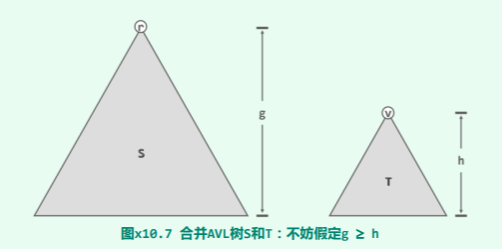首先如图 x10.7所示，不失一般性地，假定 S 的高度不低于 T——否则，以下算法完全对称。

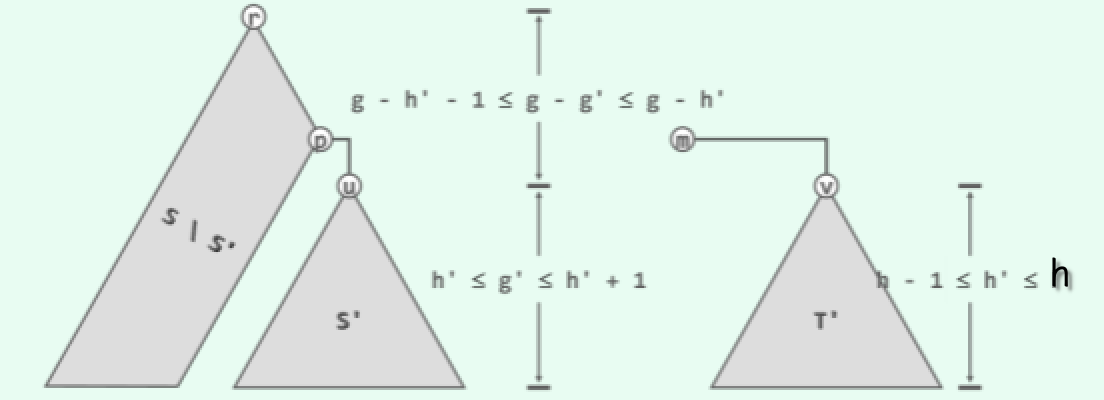设 m 为 T 中的最小节点。若将 m 从 T 中摘出，则如图 x10.8 所示，新得到的 AVL 树 T’的高度 h’必然不致增加，而且至多降低一层。 根据 AVL 树的定义，这里沿着起自根节点的任一通路每下降一层，节点的高度虽必然降低，但至多降低2。因此如图 x10.8 所示，沿着树 S 的最右侧通路，必然可以找到某个节点 u，其高度不低于 h'，而且至多比 T'高一层。将子树 u 记作 S’。

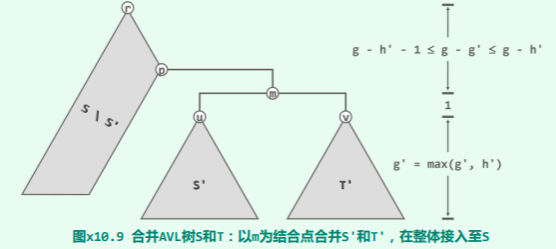于是接下来如图 x10.9所示，只要以节点 m 为联接点，将 S’和 T’分别作为其左、右子树，即可拼接成为一棵 AVL 树。

以下，将该AVL树作为节点p的右子树接入树S中，则只有p及其祖先可能失衡。因此，只需从p出发上溯并逐层核对平衡性，则至多在一个节点处经两次旋转，即可使全树恢复平衡。。

再计入删除节点 m 所需的 O(h)时间，以及查找节点 u 所需的 O(g - h)时间，可见以上算法的总体时间复杂度为 O(g) = O(max(g, h))。

特别地，若节点 m 已经从 T 中摘出，且节点 u 已知，则以上算法只需 O(g - h)时间，线性正比于两棵待合并树的高度之差。对于以下的 习题10-22，这一性质将至关重要。

10-22 分裂 AVL 树

说明：任给高度为 h 的一棵 AVL 树 A，以及一个关键码 e，试设计一个算法，在 O(h)时间内将 A 分裂为一对 AVL 树 S 和 T，且 S 中节点均小于 e，而 T 中的节点均不小于 e。

以关键码 e 查找路径上的各节点为界，可以按照中序遍历次序将全树 A 划分为一系列的子树。以如图 x10.10所示的树 A 为例，

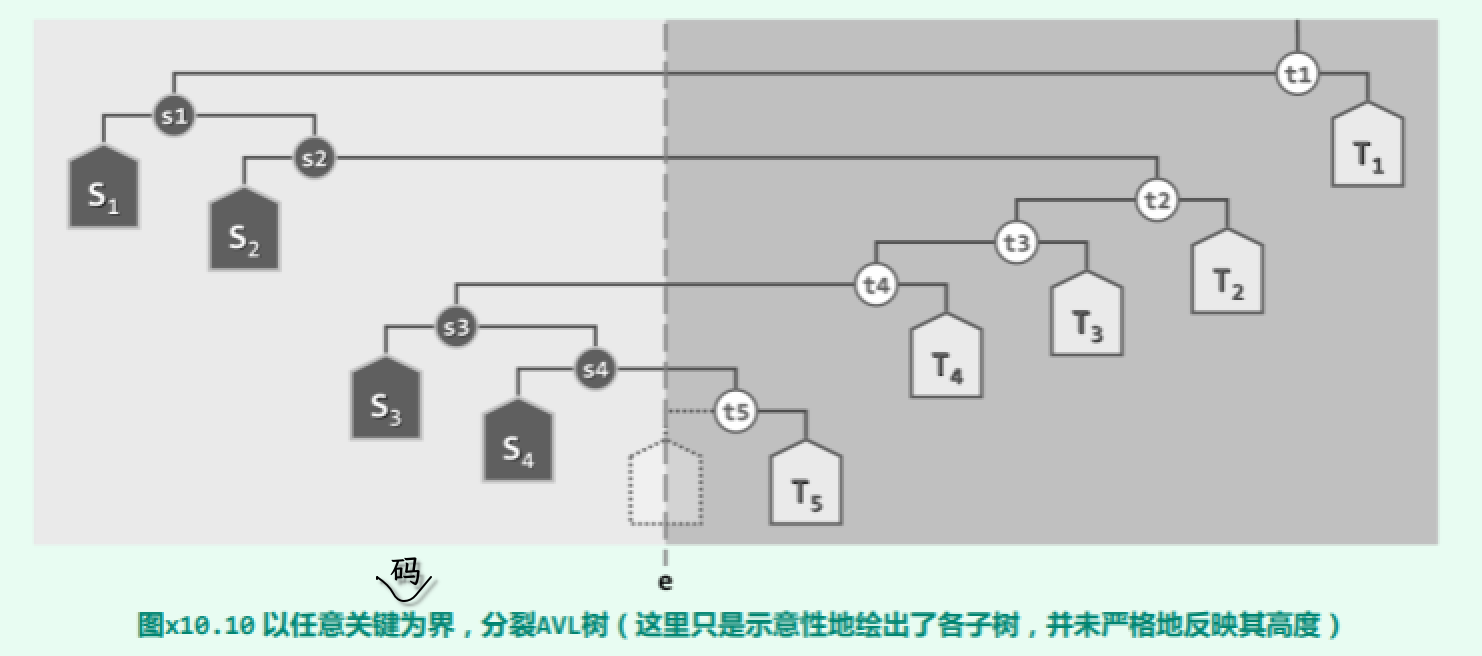
若 e 的查找路径为： t1, s1, s2, t2, t3, t4, s3, s4, t5, …

则相应地划分出来的子树依次是： T1, S1, S2, T2, T3, T4, S3, S4, T5, …

不难看出，全树的中序遍历序列应是： S1, s1; S2, s2; S3, s3; S4, s4; …; t5, T5; t4, T4; t3, T3; t2, T2; t1, T1

而分裂出的两棵 AVL 子树的中序遍历序列，则应该分别是： S = S1, s1; S2, s2; S3, s3; S4, s4; … T = …; t5, T5; t4, T4; t3, T3; t2, T2; t1, T1

因此，我们可以自底而上，通过反复的合并构造出 S 和 T。鉴于这两棵树完全对称，这里不妨仅以树 T 为例，介绍具体的合并过程：

• 一旦以 t5 为根的 AVL 子树已经构造出来，我们即可以节点 t4 为联接点，将其与 AVL 子树 T4 合并，得到一棵更大的 AVL 树；
• 接下来，再以节点 t3 为联接点，进一步地将其与 AVL 子树 T3 合并；
• 然后，再以节点 t2 为联接点，继续将新得到的 AVL 树与树 T2 合并；
• 最后，以节点 t1 为联接点，将新得到 的 AVL 树与树 T1 合并。

如此，最终即可得到所求的 AVL 树 T。 这里涉及的 AVL 树合并计算，属于 习题10-21 所指出的特殊情况：作为联接点的节点 tk， 均等效于已经从待合并子树中摘出，且接入位置已知。因此每次合并所需的时间，不超过被合并子树的高度之差。考虑到前后项的依次抵消效果，累计时间应渐进地不超过原树高度 O(h)。