71-Hash-Exercise

9-3 SkipList, AVLTree, SplayTree, (2,3)-Tree 的接口效率比较

就 search ()/get ()接口的效率而言，SplayTree 最优
就 insert ()/put ()接口的效率而言，SkipList 最优，AVLTree 优于 (2,3)-Tree
就 remove ()接口的效率而言，SkipList 最优

9-6 散列表中模余法以同间隔插入关键码

描述：假定散列表长度为 M，采用模余法。若从空开始将间隔为 T 的 M 个关键码插入其中。试证明，若 g = gcd(M, T)为 M 和 T 的最大公约数，则有：

每个关键码均大约与 g 个关键码冲突这一组关键码依次构成一个等差数列，其公差为 T。不失一般性，设它们分别是： { 0, T, 2T, 3T, …, (M - 1)T }

按照模余法，任何一对关键码相互冲突，当且仅当它们关于散列表长 M，属于同一同余类。

这里，既然 g 是 M 和 T 的最大公约数，故相对于 M 而言，这些关键码分别来自 M/g 个同余类，且每一类各有彼此冲突的 g 个关键码。

例如，其中 0 所属的同余类为： { 0, TM/g, 2TM/g, 3TM/g, …, (g-1) TM/g }
例如，若将首项为5、公差为8的等差数列： { 5, 13, 21, 29, 37, 45, 53, 61, 69, 77, 85, 93 } 作为词条插入长度 M = 12的散列表，则如图 x9.1所示，这些词条将分成： M/g = 12/gcd(12, 8) = 12/4 = 3 个冲突的组，各组均含4个词条。

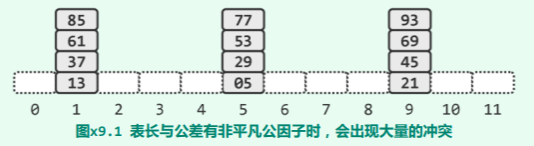
不难验证，只要是这12个词条，则无论其插入的次序如何，冲突的情况都与此大同小异。另外，采用 MAD 法的冲突情况也颇为类似。就其效果而言，在 MAD 法所用散列函数： (a * key + b ) mod M 中，b 即相当于以上算术级数的首项，a 即相当于公差 T。比如，就上例而言，有： a = 8 和 b = 5

由此也可从一个侧面理解，为何 M 和 a 的取值通常都必须二者互素——如此便有： M/gcd(M, a) = M/1 = M 从而最大程度地保证散列的随机性和均匀性。

若不采取排解冲突的措施，散列表的利用率约为 1/g 根据以上分析，散列表中的 M 个桶与 M 的 M 个同余类一一对应。既然此时的关键码只可能来自其中的 M/g 个同余类，故必有 M - M/g 个桶闲置，空间利用率不超过： M/g/M = 1/g

9-7 表长不能取作 2^k 的分析

若取 M = 2^k，则对任何词条 key 都有： key % M = key & (M - 1) = key & 00…011…1 其中，“%”和“&”分别是算术取模运算和逻辑位与运算，00…011…1中共含 k 个“1”。

于是，此时采用模余法的效果，等同于从 key 的二进制展开式中截取末尾的 k 个比特。也就是说，词条 key 更高的其余比特位对散列的位置没有任何影响，从而在很大程度上降低了散列的随机性和均匀性。

素数的作用

据说：M 为素数时，数据对散列表的覆盖最充分，分布最均匀若取 M=2^k，效果相当于截取 key 的最后 k 位，前面的 n-k 位对地址都没有影响：

M-1 = 0000… 0|11… 11

key % M = key & (M-1)

推论：发生冲突时，当且仅当最后 k 位相同，此时发生冲突的概率极大

因而，取 M != 2^k，缺陷会有所改善

从而，M 为素数时，数据对散列表的覆盖最充分、分布最均匀

蝉的哲学：经长期自然选择，生命周期“取”作素数

蝉通常是十三龄蝉、十七龄蝉这样的素数年龄；

这里十三龄、十七龄就是除余法中的 M，而 step 是天敌的生命周期；

指向原始笔记的链接

9-13 避免平方试探法中的乘法运算

要求：在实现平方试探法时，可否只使用加法而避免乘法（平方）运算？

事实上，若散列表长为 M，则对于任意非负整数 k，都有： $(k + 1)^{2} \equiv k^{2} + (k + k + 1) (m o d M)$ 只要注意到这一规律，在前一桶地址（k^2 % M）的基础上，只需再做三次加法运算，即可得到下一桶地址（(k + 1)^2 % M）。

9-14 单向平方试探法表长为素数的查找链分析

==表长 M 为素数，证明任一关键码对应的查找链中，前 $⌈ \frac{M}{2} ⌉$ 个桶必然互异== 反证。假设存在0 ⇐ a < b < $⌈ \frac{M}{2} ⌉$ ，使得查找链上的第 a 个位置与第 b 个位置冲突，于是 $a^{2}$ 和 $b^{2}$ 必然同属于关于 M 的某一同余类，亦即： $a^{2} \equiv b^{2} (m o d M)$ 于是便有： $a^{2} - b^{2} = (a + b) \cdot (a - b) \equiv 0 (m o d M)$ 然而，无论是(a + b)还是(a - b)，绝对值都严格小于 M，故均不可能被 M 整除——这与 M 是素数的条件矛盾。
证明：装填因此λ尚未增至 50% 前，插入操作必然成功（不致因无法抵达空桶而失败）由上可知，查找链的前 $⌈ \frac{M}{2} ⌉$ 项关于 M，必然属于不同的同余类，也因此互不冲突。在装填因子尚不足50%时，这 $⌈ \frac{M}{2} ⌉$ 中至少有一个是空余的，因此不可能发生无法抵达空桶的情况。
证明：装填因子超过 50% 后，只要适当调整各桶的位置，下一插入操作必然因无法抵达空桶而失败。思路：只需证明， ${0^{2}, 1^{2}, 2^{2}, ...}$ 关于 M 的同余类恰好只有 $⌈ \frac{M}{2} ⌉$ 个

任取： $⌈ \frac{M}{2} ⌉$ ⇐ c < M - 1 并考查查找链上的第 c 项。可以证明，总是存在0 ⇐ d < $⌈ \frac{M}{2} ⌉$ ，且查找链上的第 d 项与该第 c 项冲突。实际上，只要令： $d = M - c \neq = c$ 则有： $c^{2} - d^{2} = (c + d) \cdot (c - d) = M \cdot (c - d) \equiv 0 (m o d M)$ 于是 c^2和 d^2关于 M 同属一个同余类，作为散列地址相互冲突。

9-15 散列表长为合数时的平方试探

举例：散列表长为合数 M 时，装填因子低于 50%，平方试探仍有可能无法终止考查长度为 M = 12的散列表。不难验证，{ 0^2 , 1^2 , 2^2 , 3^2 , 4^2 , … }关于 M 模余数只有{ 0, 1, 4, 9 }四种可能。于是，即便只有这四个位置非空，也会因为查找链的重合循环，导致新的关键码0无法插入。而实际上，此时的装填因子仅为： λ = 4/12 < 50%
为何 M 为合数时这一问题更易出现？此时，对于秩0 ⇐ a < b < $⌈ \frac{M}{2} ⌉$ ，即便 $a + b \equiv 0 (m o d M)$ $a - b \equiv 0 (m o d M)$ 均不成立，也依然可能有： $a^{2} - b^{2} = (a + b) \cdot (a - b) \equiv 0 (m o d M)$

作为实例，仍然考查以上长度 M = 12的散列表，取 a = 2和 b = 4，则 $2 + 4 = 6 \equiv 0 (m o d 12)$ $2 - 4 = - 2 \equiv 0 (m o d 12)$ 均不成立，然而依然有： $2^{2} - 4^{2} = - 12 \equiv 0 (m o d 12)$

9-16 懒惰删除的改进方法分析

描述：随着装填因子增大，查找操作的成本将急剧上升。为克服返一缺陷，有人考虑在本章所给示例代码的基础上，做如下调整：

每次查找成功后，都随即将命中词条前移至查找链中第一个带有懒惰删除标记的空桶（若的确存在且位于命中词条之前）
每次查找失败后，若查找链的某一后缀完全由带懒惰删除标记的空桶组成，则清除它们的标记试问，这些方法是否可行？为什么？

不可行。这些方法均旨在及时地剔除带有懒惰删除标记的桶，实质上都等效于压缩查找链。设计者希望在花费一定时间做过这些处理之后，使得后续的查找得以加速，同时空间利用率也得以提高。然而对于闭散列而言最大的难点在于： 查找链可能彼此有所重叠，且任何一个带有懒惰删除标记的桶，都可能同时属于多个查找链。因此其中某一条查找链的压缩，都将可能造成其它查找链的断裂。因此为使这些策略变得可行，还必须做更多的处理，但通常都未免弄巧成拙，得不偿失。

9-17 双向平方试探的表长分析

==试证明，只要散列表长取作素数 M = 4k + 3（k 为非负整数），则：任一关键码所对应的查找链中，前 M 个桶必然互异（即取遍整个散列表）== （提示：任一素数 M 可表示为一对整数的平方和，当且仅当 $M \equiv 1 (m o d 4)$ ——费马平方和定理）

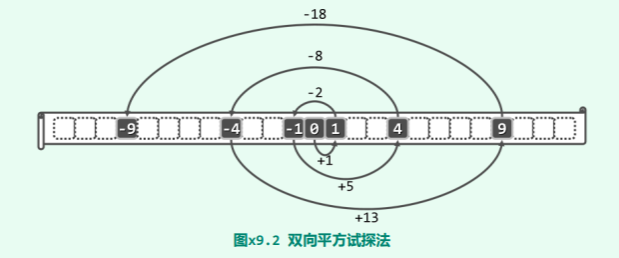
使用双向平方试探法，根据跳转的方向，查找链的前 M 项可以分为三类：

第 1 次试探，位于原地的起点
第 2、4、6、…、M - 1 次试探，相对于起点向前跳转
第 3、5、7、…、M 次试探，相对于起点向后跳转

根据习题9-14的结论，无论 $1 \cup 2$ 还是 $1 \cup 2$ ，其内部的试探均不致相互冲突。因此，只需考查 2 类与 3 类试探之间是否可能冲突。

假设第 2a 次（2 类）试探，与第2b + 1次（3 类）试探相互冲突。于是便有： $a^{2} \equiv - b^{2} (m o d M)$ 亦即： $n = a^{2} + b^{2} \equiv 0 (m o d M) ............. (*)$

然而以下将证明，对于形如 M = 4k + 3的素数表长，这是不可能的。一个自然数 n 若可表示为一对整数的平方和，则称之为“可平方拆分的”。不妨设 n 的素因子分解式为： $n = p_{1}^{α 1} \cdot p_{2}^{α 2} \cdot p_{3}^{α 3} \cdot ... \cdot p_{d}^{α d}$ 只要注意到以下恒等式： (u^2 + v^2 )(s^2 + t^2 ) = (us + vt)2 + (ut - vs)2

即不难理解，n 是可平方拆分的，当且仅当对于每个1 ⇐ i ⇐ d，或者 $α_{i}$ 是偶数，或者 $p_{i}$ 是可平方拆分的。除了2 = 1^2 + 1^2，其余的素数可以按照关于4的模余值，划分为两个同余类。而根据费马平方和定理，形如4k + 1的素因子必可平方拆分，而形如4k + 3的素因子则必不可平方拆分。因此 n 若可平方拆分，则对于其中每个形如 $p_{i} = 4 k + 3$ 的素因子， $α_{i}$ 必然是偶数。

现在，反观以上( * )式可知，M = 4k + 3应是 n 的一个素因子。而根据以上分析还可进一步推知，n 必然能被 M^2整除。于是便有: n = a^2 + b^2 >= M^2 然而，对于取值都在 $[1, ⌊ \frac{M}{2} ⌋]$ 范围之内的 a 和 b，这是不可能的。

由上，可知装填因子未达 100%前，插入操作必然成功。

9-18 散列表实例

散列表长：|H| = 11
确定散列地址的方法：除余法
排解冲突的方法：单向平方试探法
删除操作：懒惰删除策略

通过 put ()接口插入{2012,10,120,175,190,230}，给出各桶单元中的内容。按照除余法，这一组关键码对应的初始试探位置依次为： { 10, 10, 10, 10, 3, 10 } 因此整个插入过程应该如下：

2012 可直接存入 10 号桶
10 经过 2 次试探，存入 (10 + 1) % 11 = 0 号桶
120 经过 3 次试探，存入 (10 + 1 + 3) % 11 = 3 号桶
175 经过 4 次试探，存入 (10 + 1 + 3 + 5) % 11 = 8 号桶
190 经过 2 次试探，存入 (3 + 1) % 11 = 4 号桶
230 经过 6 次试探，存入 (10 + 1 + 3 + 5 + 7 + 9) % 11 = 2 号桶最终结果，如图所示：

若执行 remove (2012), 试给出此时各桶单元内容
若再执行 get (2012)，会出现什么问题？不难验证，形如： (10 + k^2 ) % 11, k = 0, 1, 2, 3, … 的整数只有6种选择： { 0, 2, 3, 4, 8, 10 } 它们构成了2012所对应的查找链。

然而反观如图 x9.4所示的当前散列表可见，此时该查找链上所有的桶均非空余——其中5个存有关键码，1个带有懒惰删除标记。因此，对2012的查找必然陷入死循环。

如何修改以避免此类问题？首先，在计算装填因子时，可以同时计入带有懒惰删除标记的桶。这样，一旦发现装填因子超过50%，则可通过重散列及时地扩容，令装填因子重新回落至50%以下——根据习题9-14的结论，如此即可保证，查找过程必然不致出现死循环。

另外，也可以改用习题9-17所建议的双向平方试探法排解冲突。当然，此后如需通过重散列扩容，则散列表的容量 M 必须与初始的11一样，依然是形如4k + 3的素数。

9-23 计数排序

描述：若将任一有序序列等效地规作有序向量，则其中每个元素的秩，应恰好就等于序列中不大于该元素的元素总数。例如，其中最小、最大元素的秩分别为 0、n - 1，可以解释为：分别有 0 和 n - 1 个元素不大于它们。根据这一原理，只需统计出各元素所对应的这一指标，也就确定了它们在有序向量中各自所对应的秩。

基于以上思路，设计一个排序算法。

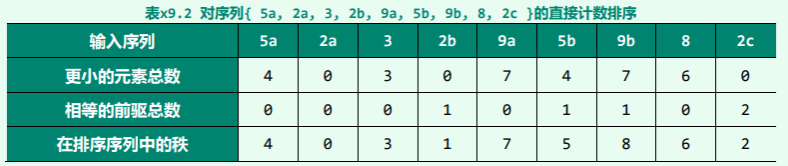
为每个元素设置一个计数器，初始值均取作0。以下对于每个元素，都遍历一趟整个序列，并统计出小于该元素的元素总数，以及在位于该元素之前、与之相等的元素总数(自后向前)。最后，根据以上两项之和，即可确定各元素在排序序列中对应的秩。仍如教材277页图9.21所示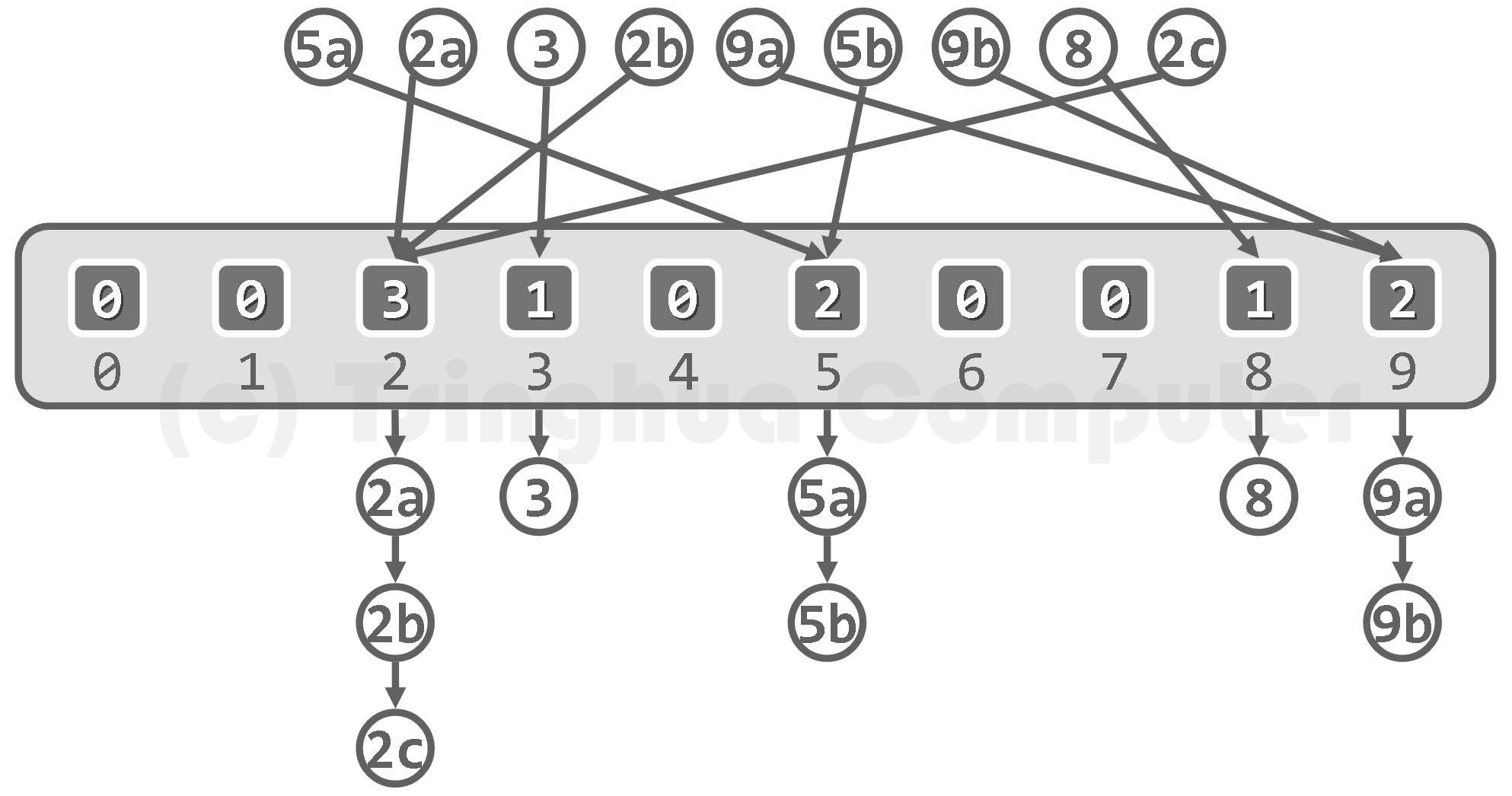，考查待排序序列{ 5a, 2a, 3, 2b, 9a, 5b, 9b, 8, 2c } 按照以上算法，每个元素的各项统计数值如表 x9.2所示。对照教材的图9.21可见，排序结果完全一致。

分析时间复杂度和空间复杂度。该算法供需 O(n)趟遍历，每趟遍历均需 O(n)时间，故累计耗时为 O(n^2 )。除了原输入序列，这里引入的计数器还共需 O(n)辅助空间。
改进算法，使得能在 O (n+M)时间内对来自[0, M)范围内的 n 个整数进行排序，且使用的辅助空间不超过 O (n)

int* countingSort(int A[0, n))
	引入一个可计数的散列表H[0, M)，其长度等于输入元素取值范围的宽度M
	将H[]中所有桶的数值，初始化为0
	遍历输入序列A[0, n) //遍历计数，O(n)
		对于每一项A[k]，令H[ A[k] ] ++
	遍历散列表H[0, M) //逐项累加，O(M)
		对于每一项H[i]，令H[ i + 1 ] += H[i]
	创建序列S[0, n)，用以记录排序结果
	逆向遍历输入序列A[0, n) //逐项输出，O(n)
		对于每一项A[k]
			令S[ -- H[ A[k] ] ] = A[k]
	返回S[0, n)

同样地，也请读者特别留意这里对输入序列和散列表的扫描方向，并体会为何如此可以保证该算法的稳定性。

其中每个步骤各自所需的时间，如注释所示。总体而言，执行时间不超过 O(n + M)。需要特别说明的是，若 n >> M，则排序时间为 O(n)，优于面向一般情况最优的 O(nlogn)。另外从算法流程这也就是所谓的“小集合、大数据”情况，在当下实际应用中，这已成为数据和信息处理的主流需求类型。

空间方面，除了输出序列 S[]，这里只引入了一个规模为 O(M)的散列表。仍以教材277页图9.21中序列为例。按照以上算法，所有元素各项统计数值如表 x9.3所示。

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索