D0-Hazard-of-Overfitting

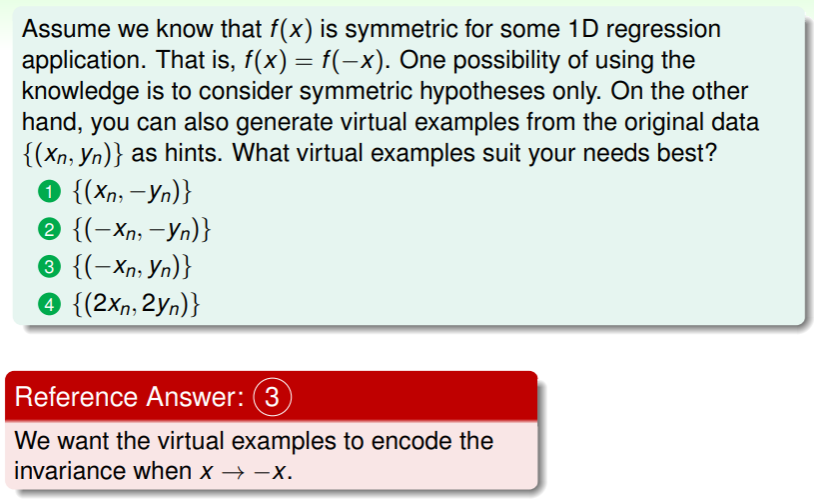
What is Overfitting?

Bad Generalization and Overfitting

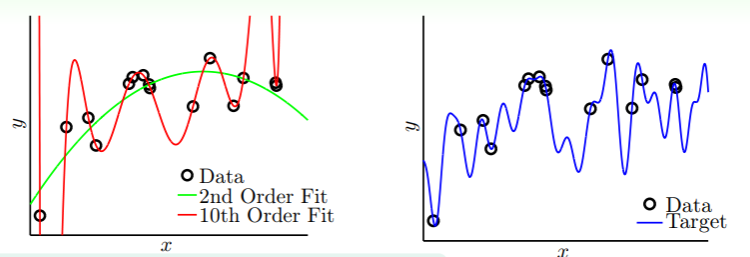
思考这样的例子：在一维空间中进行回归分析，样本数量 $N=5$ ：

• 若已知目标函数是一个二次函数，这些样本的 laebl 是目标函数与一些噪音的混合：$y_n=f({\mathbf{x}}_n)+\text{noise}$ ，此时在五个样本上预测的错误率 $E_{in}\to 0$ 虽然极小但又不完全是 0 ；
• 但若使用特征转换到四次函数的空间，使得 $E_{in}=0$ ，但是得到的预测函数与目标函数 $f$ 相去甚远，即 $E_{out}$ 非常大 ；
• 
• 这样 $E_{in}$ 很小而 $E_{out}$ 很大的例子称为 bad generalization ，即无法举一反三。

回到这幅图：

• 
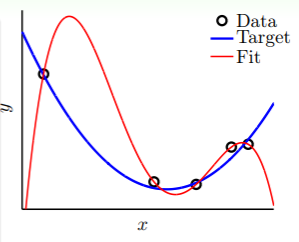
• 在从 $d_{VC}^{\ast }$ 增加到 $d_{VC}^{huge}$ 的过程就是 overfitting ，此时 $E_{in}$ 降低而 $E_{out}$ 反而增加；
• 而在从 $d_{VC}^{\ast }$ 减少到 $d_{VC}^{small}$ 的过程就是 underfitting ，此时 $E_{in}$ 增加而 $E_{out}$ 也同样增加。

区分 bad generalization 与 overfitting

前者是一个状态，后者是一个过程。

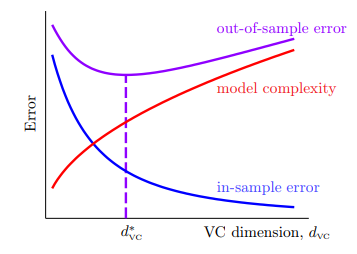
以车祸作比来理解“好的拟合”与“过拟合”：

• 
• 如果过拟合比作发生了车祸，那么导致车祸的原因有很多，
  • 比如车速太快，这就像选取了过高维度的假设集，即 $d_{VC}$ 太大了；
  • 还有可能是道路不平，这就像样本中的噪音；
  • 还有可能对道路情况的了解不够全面，这就相当于样本数量太少，在过小的局部里做到好的拟合，放到大场面就不适配了；

练习：理解 overfitting

The Role of Noise and Data Size

考虑噪音和数据集大小对过拟合的影响。

我们考虑这样两种情景：

• 
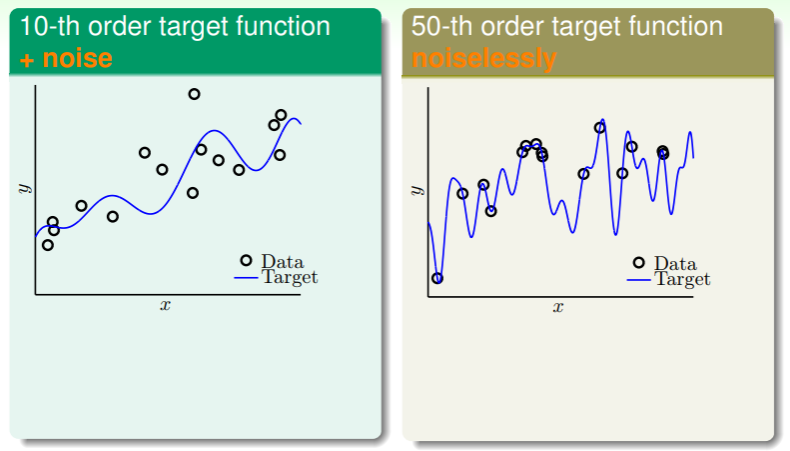
• 左图的目标函数是十次多项式，不过采样的样本有一些噪音；
• 右图的目标函数是五十次多项式，采样的样本没有噪音，完全吻合；

我们试图使用两种假设集——二维假设集 ${\mathcal{H}}_2$ 和十维假设集 ${\mathcal{H}}_{10}$ ——并从中选取各自最佳的估计 $g_2$ 或 $g_{10}$ 来考虑：

• 
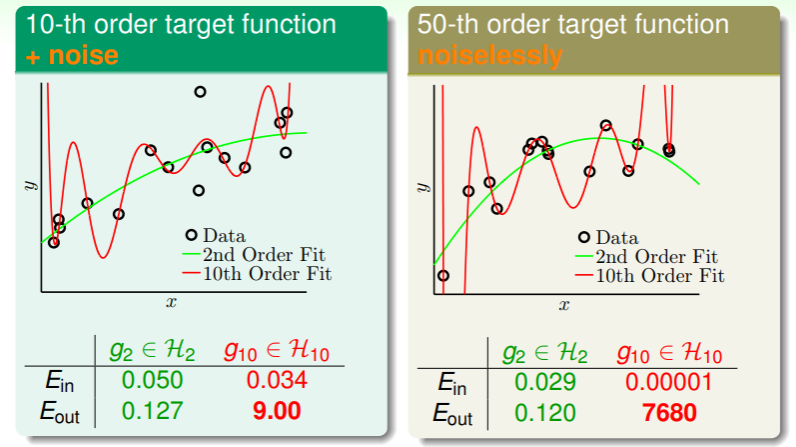
• 左图情形是无噪音的，其中二维假设 $g_2$ 和 十维假设 $g_{10}$ 在 $E_{in}$ 的表现上都不错，并且十维假设与目标函数更加接近，因此 $E_{in}(g_{10})$ 更低一些；不过在查看 $E_{out}$ 时（可以理解为 $g_i$ 与 目标函数 $f$ 的相似度），两种假设的 $E_{out}$ 都显著高于各自的 $E_{in}$，尤其是 $g_{10}$ 不相似度达到了 9.00 之多；
• 右图情形是无噪音的，类似的，$g_2$ 和 $g_{10}$ 在 $E_{in}$ 上都很小，并且 $g_{10}$ 的表现尤其不错，几乎达到了完全拟合；但是在查看 $E_{out}$ 时，$E_{out}(g_2)$ 虽然与 $E_{in}(g_2)$ 差了有十倍，而 $E_{out}(g_{10})$ 达到了一个天文数字；
• 这两种情形中过拟合都发生了，而且 “能力越强”的估计 $g_{10}$ 发生过拟合的现象越严重；

这看起来有些讽刺：“能力较差”的估计 $g_2$ 在 $E_{out}$ 上的表现远胜于“能力较强”的估计 $g_{10}$ ：

• $g_2$ 无论在哪个目标函数的情形中都无法做到 $E_{in}$ 足够小，因为它无法表示超过二次多项式的高阶多项式，但是似乎实现了“以退为进”，让渡一部分 $E_{in}$ 却获得了更佳的 $E_{out}$ ；
• $g_{10}$ 在左图情形似乎可以表现出所有的十阶多项式，但是由于噪音的存在它为了拟合噪音，因此始终与目标函数有所差距：
• 试着画出这两种假设在不同规模的数据集中的表现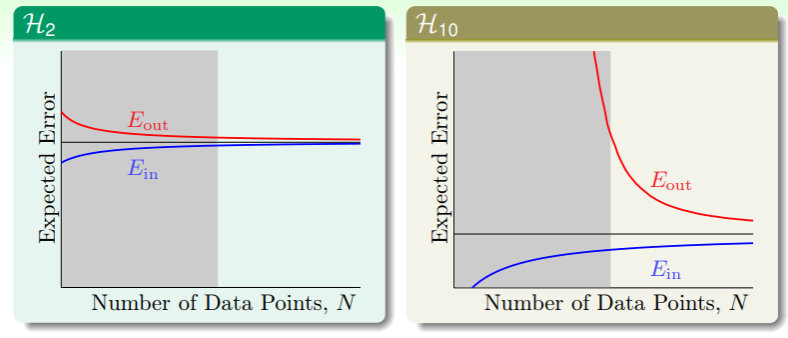： 灰色区域是 overfit 发生的区域：
  • 虽然高维假设集 ${\mathcal{H}}_{10}$ 的估计在数据集规模 $N\to +\infty$ 时能够做到 $\overline{E_{in}}$ 相当小，但是在数据集规模不足时，$\overline{E_{out}}$ 与 $\overline{E_{in}}$ 相去甚远；
  • 甚至可以说，“能力较差”的估计 $g_2$ ，在数据集规模不够大时，总是表现更佳的！

另一个没有噪音的情形里：

• 
• “能力较差”的估计 $g_2$ 亦然表现更佳，虽然这两种估计都无法实现五十阶的多项式，并且由于没有噪音的存在，按理说 $g_{10}$ 的表现应该比 $g_2$ 更佳才对，毕竟 100 分的试卷虽然都无法全部做对，但是能力更强的 $g_{10}$ 同学应该得分更高？
• 事实上真的没有噪音吗？其实在从五十维降维到二维、十维的过程中，损失的精度都是 noise ，超过本身能力的复杂度在这里扮演的角色就是 noise！

练习：理解噪音与数据集规模对 $E_{out}$ 的影响

• 这里 R 指的是“能力较差”的估计，如 $g_2$ ，
• O 指的是“能力较强”的估计，如 $g_{10}$ ；

Deterministic Noise

How Overfitting Occurs？

我们继续仔细考虑噪音和数据集规模对过拟合现象的影响：

首先对于噪音，可以表示成每个样本的 label 与目标函数的一点小的偏差：$y=f(\mathbf{x})+ϵ$ ，这里噪音 $ϵ$ 服从正态分布：$ϵ\sim N\left(\underset{f(\mathbf{x})}{\underbrace{\sum _{q=0}^{Q_f}{\alpha }_q{\mathbf{x}}^q}},{\sigma }^2\right)$ ，

• 这里 $Q_f$ 表示目标函数是 Q 次方的一个均匀分布（为何要均匀分布？因为五十维空间里的目标函数不一定就是五十阶的多项式，完全可以是一个三十二阶多项式甚至零阶多项式）
• ${\sigma }^2$ 表示噪音的离散程度，即噪音对数据集影响的强度；

接着我们在两种假设 $g_2$ 和 $g_{10}$ 中，看看当噪音强度 ${\sigma }^2$ 、数据集规模 $N$ 、目标函数的复杂程度 $Q_f$ 不同时，对过拟合程度的影响究竟是什么？

• 过拟合程度的评估不妨以不同假设的 $E_{out}$ 之差 $E_{out}(g_{10})-E_{out}(g_2)$ 的大小作为考量，那么我们就得到这样的图像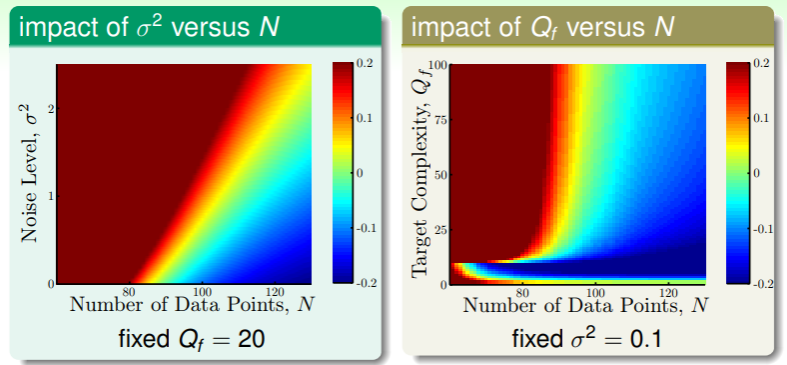： 红色越深代表过拟合程度越高，蓝色越深表示拟合程度越好；ps. 这就是 课程 logo 的来源😆
• 左图告诉我们，对于固定的目标函数复杂度：
  • 在数据集较小、噪音强度较大时，过拟合程度很高；
  • 而在数据集越大、噪音强度越低，拟合准确度越好；
• 右图告诉我们，对于固定的噪音强度：
  • 两幅图都大致是在数据集较小时容易发生过拟合，这就是“目标函数的复杂度充当了噪音一角”的结论的来源；
  • 不过与随机噪音强度不同的是，目标函数的复杂度不是随机的，它是服从均匀分布的，因此相对完全随机的噪音（stochastic noise），我们可以称之为特定的噪音（deterministic noise）；
  • 另外右图与左图还有一个差别，在目标函数复杂度不超过 10 时有一个几乎水平的分界线，并且在这个局部，
    • 当数据集越小、目标函数复杂度越低时过拟合程度越高，这很好理解，$g_{10}$ 能力太强了，超出了目标函数复杂度的需求，因此产生了过拟合，
    • 而随着数据集规模的增加，过拟合程度迅速地降低，这也好理解，能力强的 $g_{10}$ 多加训练，自然能够获得更好的效果；

总结起来，其实过拟合非常容易发生，在以下四种情形里尤其容易，因此我们在进行 ML 建模时要格外注意避免：

1. 数据集规模 $N$ 过小，
2. 随机噪音强度 ${\sigma }^2$ 过大，这表明数据集的可信度、可用度都有待考虑，
3. 目标函数复杂度 $Q_f$ 过大，这表明不要强迫有限能力的假设完成它做不到的事，除非给它足够量的训练，
4. 过于强力的假设 ${\mathcal{H}}_{\text{too large}}$ ，即过于复杂的假设在简单的目标函数复杂度时往往大材小用，甚至把噪音也一并拟合进去，所以过拟合发生；

Details of Deterministic Noise

如果目标函数超越了假设的能力范围，那么无论如何挑选假设 $g$ ，都必然无法实现完全的拟合，这就是 deterministic noise ：

• 灰色部分表示目标函数 $f$ 与假设集中最佳的估计 $h^{\ast }$ 在同一个样本上的差距，也就是 deterministic noise ：
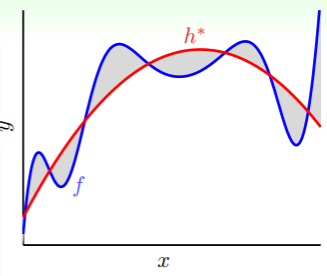
• 不过这种噪音与随机噪音还是有这本质差别，
  • deterministic noise 一方面依赖于假设集 $\mathcal{H}$ 的复杂度，理论上假设集的复杂度越大，那就与目标函数的差距越小（尽管有可能在数据量不足时过拟合）；
  • 另外对于固定的样本，deterministic noise 是固定的，而不会变化。

Analogy

其实 Human Learning 在这方面与 Machine Learning 表现类似，就像教小孩子学数学，1+1=2 时拿苹果举例子更合适，而不是从群论、数论开始讲😆

练习：理解 deterministic noise

• 用线性函数自然无法拟合 sin 函数，要使其最佳，就只能是水平的直线；

Dealing with Overfitting

从过拟合发生的条件来看，我们可以有以下方法降低过拟合发生的概率：

• 从简单的模型开始训练：就像为了避免过拟合这一“车祸”，我们可以首先开慢一点；
• 做好数据清理与剪枝，降低噪音的影响：就像我们可以通过获知更详细的路况来避免车祸；
• 数据量不足时，我们可以运用 data hinting 的方法获得 virtual 但是正确的数据：就像在全部路况不清楚时，先仔细察看附近的路况一样；
• 可以使用 regularization ：这类似于放心大胆地开车，遇到问题时交给刹车来解决；
• 可以使用验证集 ： 这类似于开车过程中随时检查仪表盘的数据和信息；

Data Cleaning / Pruning

我们可以通过许多手段在训练前就检查数据集的噪音强度，比如如果某个 label 为 $\circ$ 的样本过于接近其它 $\times$ 的样本而远离 $\circ$ 样本，那就有可能是噪音……

修正噪音的 label ，称为 data cleaning ；而移除噪音样本，称为 data pruning 。

这种手段的效果因数据集的情况而异，难以确定收效。

Data Hinting

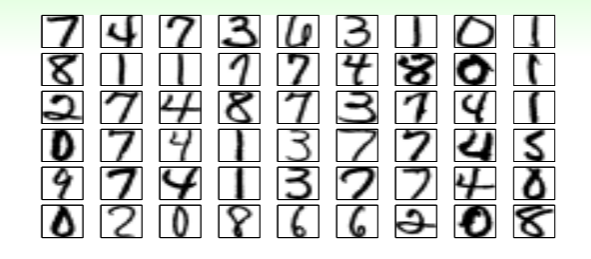
如果数据集只有这些样本，那么该怎么训练呢？一种方法是，对样本进行微小的调整，诸如移动、拉伸、旋转等，但又不改变其 label，从而获得更丰富的数据集。

这种方法称为 data hinting ，经过微调的样本称为 virtual examples ，不过要注意的是，这些 virtual examples 不再是独立同分布于 $P(\mathbf{x},y)$ 的。

练习：理解 data hinting